Geometry Semester 2 Practice Exam Answer Key

Preparing for a challenging math assessment requires a clear understanding of key concepts and the ability to solve problems efficiently. This section provides valuable resources to help you evaluate your knowledge and practice critical problem-solving techniques. With accurate solutions at your fingertips, you can strengthen your skills and boost your confidence.

By carefully working through the problems and comparing your responses with the provided solutions, you can identify areas for improvement. This approach allows you to refine your strategies, ensuring that you are well-prepared for any related test. Emphasizing clear explanations and step-by-step breakdowns, this guide offers a structured way to tackle even the most complex mathematical challenges.

Use the materials effectively to enhance your understanding and sharpen your problem-solving abilities. With consistent practice and the right guidance, you’ll be able to approach your next assessment with greater ease and precision.

Geometry Semester 2 Exam Overview

This section provides a comprehensive look at the final assessment for this course, covering a range of important mathematical concepts. The focus will be on understanding and applying various problem-solving techniques that are crucial for demonstrating mastery in the subject. You will encounter questions designed to test your knowledge across several key areas, each requiring a detailed and logical approach.

The evaluation will include a mix of questions that assess your ability to calculate, interpret, and analyze different types of mathematical scenarios. Whether it involves solving equations, working with shapes, or applying formulas, the test is structured to challenge your skills and ensure a well-rounded understanding of the material covered throughout the term.

Key Topics Covered in Semester 2

This section highlights the critical subjects explored during the second half of the course, each focusing on essential mathematical principles and techniques. The material challenges students to deepen their understanding and refine their problem-solving skills, ensuring a thorough grasp of advanced topics. Below is an outline of the key concepts addressed, which form the foundation of the final assessment.

Topic	Description
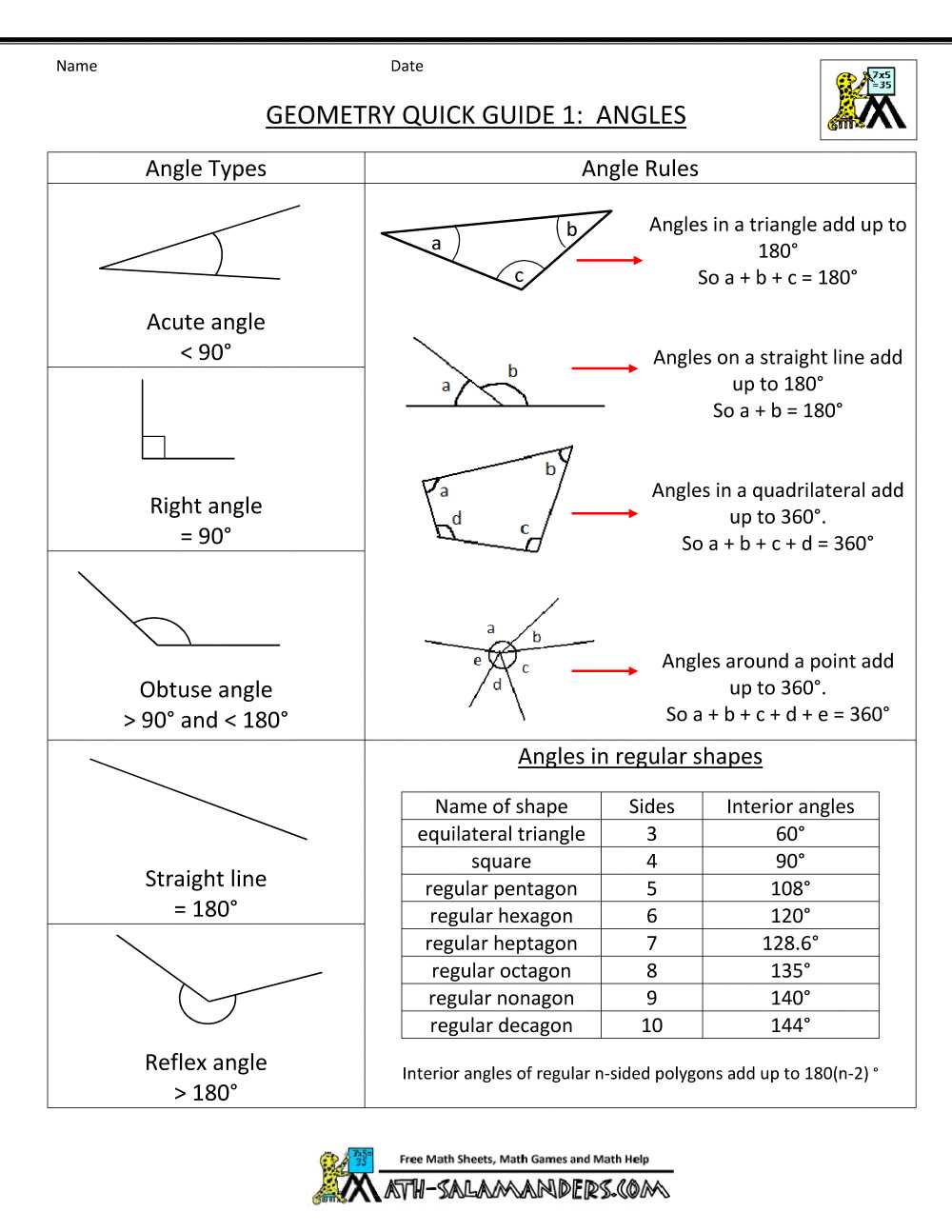
Angles and Their Properties	Understanding the different types of angles and how they relate to each other in various geometric configurations.
Area and Perimeter Calculations	Methods for calculating the area and perimeter of various polygons and complex figures.
Volume and Surface Area	Techniques for determining the volume and surface area of 3D shapes such as spheres, cones, and pyramids.
Coordinate Geometry	Analyzing geometric figures using the coordinate plane, including distance and midpoint formulas.
Trigonometric Ratios	Exploring sine, cosine, and tangent functions to solve real-world problems involving right triangles.

How to Use the Answer Key Effectively

Utilizing a solution guide can significantly enhance your preparation by offering a detailed breakdown of problem-solving methods. It’s important to approach the guide strategically, ensuring you understand the logic behind each step rather than simply checking your responses. This approach will help you identify patterns, avoid common mistakes, and strengthen your overall grasp of the material.

Start by attempting the problems independently, and once you have completed them, use the guide to review your work. Focus on understanding where and why you went wrong, and ensure that you grasp the reasoning behind each solution. This way, you can learn from your errors and refine your techniques for future problems.

In addition, don’t hesitate to revisit topics you find challenging. The solution guide can serve as a tool to clarify difficult concepts by providing alternate approaches and additional explanations. Using this resource actively will not only improve your understanding but also increase your confidence in tackling similar questions.

Common Mistakes to Avoid in Geometry

When working through mathematical problems, it’s easy to make mistakes that can hinder your progress and affect your understanding. Recognizing these common errors and knowing how to avoid them is essential for improving your skills. Below are some of the most frequent mistakes students make and tips on how to overcome them.

• Misinterpreting Problem Statements: Not fully understanding the problem can lead to incorrect solutions. Always take time to read each question carefully and highlight key information.
• Forgetting Units: Whether it’s calculating area, volume, or length, neglecting to include the correct units can lead to incomplete answers. Be consistent with your units throughout.
• Skipping Steps: Rushing through problems or skipping intermediary steps can lead to small errors that compound into larger mistakes. Always show your work to ensure clarity and accuracy.
• Incorrect Use of Formulas: Using the wrong formula or applying it incorrectly is a common issue. Make sure to double-check the formula before applying it to solve the problem.
• Overlooking Special Cases: Some problems require special treatment, such as undefined values or exceptions. Always watch out for these nuances and adjust your approach accordingly.

By being mindful of these pitfalls, you can improve both your accuracy and confidence when solving problems.

Step-by-Step Solutions for Practice Problems

Breaking down complex problems into smaller, manageable steps is a highly effective way to grasp difficult concepts. This section provides clear, systematic solutions to help you understand the process behind each problem. By following the steps outlined, you can improve your ability to tackle similar challenges independently and confidently.

Example 1: Solving for Area

In this example, we will calculate the area of a polygon using the appropriate formula. The process involves identifying the correct formula, substituting the given values, and performing the necessary operations to arrive at the solution.

• Step 1: Identify the shape and the formula needed. For example, the area of a rectangle is calculated as length × width.
• Step 2: Substitute the known values into the formula.
• Step 3: Perform the multiplication to find the area.
• Step 4: Double-check your result for accuracy.

Example 2: Using Proportions to Solve Problems

In this second example, we will use proportional relationships to solve for unknown values. Understanding how to set up and solve proportions is crucial for many types of problems.

• Step 1: Write the proportion based on the given information.
• Step 2: Cross-multiply and simplify the equation.
• Step 3: Solve for the unknown value by isolating the variable.
• Step 4: Verify the solution by substituting it back into the original proportion.

By following these step-by-step instructions, you can approach any problem methodically and avoid common pitfalls, improving your problem-solving skills over time.

Understanding the Formulas You Need

Mastering the formulas relevant to your studies is essential for solving problems efficiently and accurately. Knowing when and how to apply each formula ensures that you can approach tasks with confidence. This section focuses on key formulas you’ll need to know and explains how to use them effectively in various problem-solving scenarios.

Essential Formulas for Calculations

Different mathematical problems require specific formulas. For example, the formula for the area of a triangle is Area = 1/2 × base × height. Understanding the context of the problem helps you choose the right formula. Ensure that you understand the variables involved and how they relate to the geometric figure you are working with.

Using Formulas in Multi-Step Problems

Some problems require a combination of formulas or multi-step processes. For instance, when calculating the volume of a complex figure like a cone, you may need to apply both the formula for the area of the base and the formula for volume. Carefully breaking the problem into smaller parts will make it easier to apply the appropriate formulas step-by-step.

By thoroughly understanding these formulas and practicing their application, you will be better equipped to solve even the most challenging questions with ease.

Practice Test Questions Explained

Understanding how to approach different types of problems is crucial for success. This section breaks down sample problems, offering clear, step-by-step explanations. By reviewing these examples, you can gain a deeper understanding of the thought processes and strategies needed to solve complex tasks.

Example 1: Solving for Unknown Length

In this example, we’ll solve for an unknown side length in a right triangle using the Pythagorean theorem. By identifying the known values and applying the formula, you can find the missing side with ease.

Step	Action	Formula/Explanation
Step 1	Identify the given sides.	We are given the lengths of two sides of a right triangle.
Step 2	Apply the Pythagorean theorem.	Use the formula: a² + b² = c², where c is the hypotenuse and a and b are the other two sides.
Step 3	Calculate the missing value.	Substitute the known values into the equation and solve for the unknown side.

Example 2: Finding the Area of a Circle

This example demonstrates how to calculate the area of a circle when given the radius. The formula for the area of a circle is Area = π × r², where r is the radius.

Step	Action	Formula/Explanation
Step 1	Identify the given radius.	We are provided with the radius of the circle.
Step 2	Apply the area formula.	Use the formula: Area = π × r².
Step 3	Perform the calculation.	Multiply the radius by itself and then by the value of π to find the area.

By carefully working through these examples, you can build a solid foundation of problem-solving skills that will help you tackle even the most challenging tasks with confidence.

Tips for Mastering Geometry Concepts

Mastering mathematical principles requires both understanding the foundational concepts and consistently applying them to various problems. Whether you’re learning about shapes, angles, or spatial reasoning, it’s essential to develop a strong grasp of each topic. The following tips will help you build your skills and approach challenging concepts with confidence.

1. Visualize the Problem

One of the most effective strategies for understanding complex concepts is to visualize the problem. Drawing diagrams or sketches of shapes can help clarify relationships between different elements. When you visualize the problem, it becomes easier to see patterns and apply the correct methods to solve it.

2. Practice Regularly

Repetition is key to mastering any concept. Regular practice helps reinforce your understanding and improves your problem-solving speed. Try solving a variety of problems to expose yourself to different scenarios, and aim to tackle both easy and difficult challenges. This diverse practice will build your confidence and sharpen your skills.

By consistently applying these techniques, you will deepen your understanding and become more proficient in tackling a wide range of tasks. Take the time to focus on each concept, and don’t rush the learning process.

How to Improve Your Geometry Skills

Improving your skills in mathematical reasoning and spatial relationships involves more than just memorizing formulas; it requires understanding concepts and applying them effectively to various problems. With dedication and the right approach, you can significantly enhance your ability to solve complex tasks. The following strategies will help you develop a deeper understanding and strengthen your problem-solving skills.

1. Break Down Complex Problems

One of the most effective ways to improve is by breaking problems into smaller, more manageable parts. Instead of being overwhelmed by the complexity of a task, focus on solving one step at a time. This approach not only makes the process less intimidating but also helps you spot patterns and connections between different elements more easily.

2. Use Real-World Examples

Applying theoretical knowledge to real-world scenarios can make abstract concepts more tangible. Whether you’re studying angles, shapes, or measurements, look for ways to relate them to things around you–like architecture, design, or even nature. By making connections between theory and practice, you can deepen your understanding and improve retention.

3. Collaborate with Others

Sometimes, discussing problems with peers or working in study groups can lead to new insights. Different perspectives can help you see solutions that you might have overlooked. Engaging in collaborative learning also allows you to explain concepts to others, reinforcing your own understanding in the process.

4. Stay Consistent

Improvement comes with consistent effort. Set aside time each day to review concepts, solve problems, and challenge yourself with new topics. By maintaining a regular study routine, you’ll build your skills gradually and feel more confident in tackling increasingly difficult tasks.

With time and the right mindset, these strategies will lead to noticeable improvements in your problem-solving abilities and overall understanding. Keep practicing, stay patient, and celebrate your progress along the way!

Breaking Down Complex Problems

When faced with challenging problems that involve various shapes, measurements, or relationships, it can be easy to feel overwhelmed. However, breaking down complex tasks into smaller, more manageable steps can make the process simpler and more approachable. The key is to focus on the individual elements, understand how they relate to each other, and tackle one aspect at a time.

Start by identifying all the known values and key information provided in the problem. Make a list of these elements and highlight the relationships between them. This will help you understand the structure of the problem and determine what you need to find. Often, breaking the problem into parts will reveal useful patterns or hints that weren’t initially obvious.

Once the information is organized, consider the tools or formulas that are most appropriate for solving the problem. Whether you need to apply basic principles or more advanced techniques, knowing when and how to use them is crucial. Don’t hesitate to draw diagrams or make sketches to visualize the problem–this can clarify many aspects that are difficult to grasp through numbers alone.

Finally, take your time and approach each step with care. It’s easy to rush through the solution, but paying attention to each detail ensures that you don’t overlook important elements. By breaking down the task into smaller steps, you’ll find that even the most complex problems become easier to solve.

Calculating Area and Volume in Geometry

Calculating the area and volume of various shapes is a fundamental skill that is essential for solving a wide range of mathematical problems. These calculations help determine the amount of space covered by a shape or occupied by an object. Mastering these calculations requires understanding the formulas for different figures and applying them appropriately based on the given information.

1. Area of 2D Shapes

The area refers to the total surface covered by a two-dimensional shape. Each shape has a specific formula for calculating its area. Some common ones include:

• Rectangle: Area = length × width
• Triangle: Area = ½ × base × height
• Circle: Area = π × radius²
• Square: Area = side × side

It is crucial to identify the correct dimensions for each shape before applying the formula. For example, the base and height of a triangle must be perpendicular to each other, and the radius of a circle should be measured from the center to the edge.

2. Volume of 3D Shapes

Volume, on the other hand, deals with the amount of space inside three-dimensional objects. Different solids have distinct formulas for calculating volume:

• Cube: Volume = side³
• Rectangular Prism: Volume = length × width × height
• Cylinder: Volume = π × radius² × height
• Sphere: Volume = ⁴/₃ × π × radius³

To accurately calculate volume, you need to identify the correct dimensions such as radius, height, or length. In some cases, it may be helpful to break the object into smaller, simpler shapes to simplify the calculation.

By understanding and practicing these formulas, you can gain confidence in solving problems that involve determining the area and volume of different shapes. Keep practicing to ensure that you can quickly and accurately perform these calculations in a variety of scenarios.

Solving Trigonometric Problems with Ease

Trigonometry involves studying the relationships between the angles and sides of triangles. While these problems may seem complex at first, understanding the basic principles and methods can make them much more manageable. By breaking down the steps and focusing on key concepts, you can approach trigonometric problems with confidence and ease.

One of the most important tools in solving these problems is the use of trigonometric ratios. These ratios–sine, cosine, and tangent–are fundamental in determining missing angles or side lengths in right-angled triangles. Once you familiarize yourself with the basic trigonometric identities, you will be able to apply them to a wide range of situations effectively.

1. Identify the Right Triangle and Given Information

Begin by recognizing the type of triangle you are working with, especially if it’s a right-angled triangle. Identify which sides and angles are provided in the problem. This will help you determine which trigonometric ratio to use. For example, if you know the opposite side and the hypotenuse, you can use the sine function.

2. Use the Correct Trigonometric Ratio

Once you’ve identified the relevant sides and angles, apply the appropriate trigonometric ratio. The basic ratios are:

• Sine (sin): sin(θ) = opposite/hypotenuse
• Cosine (cos): cos(θ) = adjacent/hypotenuse
• Tangent (tan): tan(θ) = opposite/adjacent

By using the correct ratio, you can easily solve for missing sides or angles. In cases where you need to find an angle, you can use the inverse trigonometric functions, such as sin⁻¹, cos⁻¹, or tan⁻¹.

3. Apply Trigonometric Identities

In more advanced problems, trigonometric identities can simplify complex expressions. These include fundamental identities like the Pythagorean identity (sin²θ + cos²θ = 1) and the angle sum identities (e.g., sin(A + B) = sinA * cosB + cosA * sinB). Understanding and applying these identities will help you manipulate and solve trigonometric equations with ease.

With these methods in mind, you can approach trigonometric problems more effectively. Practice is key to mastering these concepts, so keep solving problems to strengthen your understanding and skills.

How to Interpret Diagrams in Mathematics

Understanding diagrams is an essential skill when solving problems in mathematical fields that involve shapes, angles, and spatial relationships. A diagram often provides a visual representation of the problem, making it easier to comprehend the relationships between different elements. However, interpreting a diagram correctly requires attention to detail and an understanding of the key components it illustrates.

When approaching a diagram, start by identifying all the given information. This includes labeled sides, angles, and any other features that are marked or highlighted. It’s also important to look for hidden relationships between elements, such as parallel lines, perpendicular lines, or congruent shapes, which may not be explicitly stated but can be inferred from the diagram.

1. Identify Key Elements

Begin by looking for the most important features of the diagram:

• Points: Identify all marked points and their relationships with other elements in the diagram.
• Lines: Look for straight, curved, or angled lines and pay attention to whether they are parallel, perpendicular, or intersecting.
• Angles: Check for labeled angles, and if none are provided, look for right angles or other clues that can help determine the size of angles.
• Shapes: Recognize geometric shapes and understand their properties, such as symmetry, side lengths, and internal angles.

2. Recognize Relationships

Once you’ve identified the key elements, focus on how they are connected. Look for geometric properties and relationships such as:

• Parallel lines: These lines never intersect and may influence angle relationships.
• Congruent shapes: Identical shapes that have the same size and form.
• Complementary or supplementary angles: Angles that together form specific relationships, such as adding up to 90° or 180°.
• Symmetry: Some diagrams may contain symmetrical shapes, which can help in identifying missing parts or properties.

3. Mark and Label Important Information

As you analyze the diagram, it’s helpful to label key information directly on the image. This includes marking unknown sides, angles, or relationships you identify through logic. Labeling also helps in setting up equations or applying theorems correctly. If the diagram is complex, use colors or symbols to differentiate various elements to keep track of your analysis.

By carefully analyzing diagrams, you can extract crucial information that makes solving problems much more manageable. With practice, interpreting diagrams will become a more intuitive skill that helps you understand and solve a variety of mathematical challenges.

Proofs and How to Approach Them

In the study of mathematics, proving statements is a critical skill that helps validate concepts and establish new truths. A proof involves providing logical, step-by-step reasoning to support a given proposition or claim. While proofs may seem challenging at first, with the right approach, they become more systematic and manageable. This section will focus on strategies and methods that can help you tackle proofs effectively.

When faced with a proof, it’s essential to break down the problem into smaller, more manageable steps. Start by clearly understanding what is given and what needs to be proven. Carefully analyze the information provided in the problem, as well as any theorems, definitions, or properties that may be relevant. Once you have a solid understanding of the problem, you can begin formulating your approach.

1. Understand the Problem

Before diving into the proof, take a moment to identify the key elements:

• Given Information: What facts, measurements, or relationships are provided in the problem?
• To Prove: What is the goal of the proof? What are you trying to establish or demonstrate?
• Relevant Theorems: Which established theorems or properties apply to this problem? Refer to these tools as needed.

2. Develop a Strategy

Once you’ve identified the relevant information, think about how you can approach the problem. Consider the following strategies:

• Direct Proof: If the proof involves demonstrating the truth of a statement based on known facts, a direct approach may be appropriate. Start with the given information and logically build toward the conclusion.
• Indirect Proof: In some cases, it may be easier to prove that a statement is false and then show that this leads to a contradiction. This type of proof often uses the principle of contradiction.
• Proof by Construction: This method involves creating an example or building a structure that satisfies the given conditions, thereby proving the claim.

3. Use Clear, Logical Steps

As you work through the proof, it’s essential to present each step clearly and logically. Avoid jumping to conclusions, and always justify each step with a reason or reference to a known theorem. Make sure your argument flows coherently from one step to the next, leading to the desired conclusion. If necessary, draw diagrams to visualize the relationships between the elements you’re working with.

4. Review and Verify

Once you’ve completed the proof, take a moment to review your work. Check each step for logical consistency and ensure that you’ve used the correct properties or theorems. Verifying your reasoning is essential to making sure the proof is valid and complete.

With practice, the process of constructing and understanding proofs will become more intuitive. By developing a systematic approach and leveraging theorems and properties effectively, you can successfully tackle even the most complex mathematical challenges.

Using the Answer Key to Review Mistakes

After completing a set of problems, it’s essential to evaluate your work and identify areas where improvements can be made. One of the most effective ways to learn from mistakes is by carefully reviewing the provided solutions. This process helps pinpoint where you went wrong and deepens your understanding of the material. By analyzing your errors and comparing them to the correct methods, you can build stronger problem-solving skills and avoid repeating the same mistakes in the future.

1. Compare Your Approach

Start by reviewing the solutions step by step, comparing each part with your own work. Pay close attention to the reasoning behind each step and how it aligns with the problem requirements. Often, mistakes are made in the early stages of solving a problem, which can lead to incorrect results later. By identifying where your process deviates from the correct path, you can uncover the specific misunderstanding or gap in your knowledge that led to the mistake.

2. Understand Why the Mistake Happened

Once you’ve identified where your solution went wrong, try to understand why it happened. Did you misinterpret the problem? Were you confused by a particular concept or formula? Did you overlook an important detail? Understanding the cause of your error is crucial, as it allows you to prevent similar mistakes in the future. Take note of any patterns in your errors, such as misapplying a formula or overlooking key information, and work on strategies to avoid these pitfalls moving forward.

3. Break Down the Correct Solution

Take the time to fully understand the correct solution. Read through each step carefully and ensure you comprehend the reasoning behind it. This process helps reinforce key concepts and solidifies your understanding. If a specific step or method is unclear, look for additional resources or examples that explain it in a different way. The more thoroughly you understand the solution, the better you’ll be at applying similar techniques to future problems.

4. Practice Similar Problems

Once you’ve reviewed your mistakes and understood the correct methods, reinforce your learning by practicing similar problems. This will help you internalize the concepts and improve your problem-solving skills. Focus on the areas where you struggled and keep practicing until you’re confident in your ability to solve those types of problems accurately. Repetition is key to mastering any concept, and consistent practice will help solidify your understanding.

Using the provided solutions to review mistakes is a powerful tool for learning. By analyzing your errors, understanding the correct methods, and practicing similar problems, you can significantly improve your skills and become more confident in your abilities. Over time, this approach will lead to greater success and mastery of the material.

Strategies for Acing the Geometry Test

To succeed on a challenging test, preparation is key. The ability to efficiently solve problems, recall important concepts, and apply logical reasoning can make a significant difference in your performance. By using a combination of strategies tailored to the subject’s unique demands, you can build confidence and maximize your chances of achieving top results. Below are some essential strategies for approaching and mastering the material, ensuring that you are fully prepared for the test day.

1. Master the Core Concepts

Start by thoroughly understanding the core principles that are likely to appear in the test. These fundamental concepts form the backbone of many problems. Review and memorize key definitions, properties, and theorems. By solidifying this foundational knowledge, you will be able to approach questions with greater ease and precision.

• Focus on shapes, angles, and their properties.
• Understand formulas for area, perimeter, volume, and surface area.
• Study important postulates and theorems like Pythagoras’ theorem or the properties of parallel lines.

2. Develop Problem-Solving Skills

Testing your ability to solve problems under time constraints requires practice. The more problems you solve, the more comfortable you will be with different question types. When working through practice problems, ensure that you understand the step-by-step processes for solving each one. Focus on breaking complex problems into smaller, manageable parts to simplify your approach.

• Start with simpler problems and gradually move to more difficult ones.
• Practice time management during mock tests to build speed and accuracy.
• Work through each problem methodically to avoid careless mistakes.

3. Use Visual Aids and Diagrams

Whenever possible, draw diagrams or visual representations to help you understand the problem better. Many questions, especially those involving shapes and angles, can be more easily understood when you visualize them. Diagrams help clarify the relationships between different elements and can often reveal shortcuts or insights that aren’t immediately obvious from the text alone.

• Label all parts of a diagram to stay organized.
• Use color-coding for angles or lines to visually distinguish relationships.
• Review previous examples where diagrams helped simplify complex problems.

4. Review Mistakes and Learn from Them

One of the most effective ways to improve is by learning from your mistakes. After completing practice problems or mock tests, review your incorrect answers carefully. Understand why you made the mistake and what you could have done differently. By identifying these weaknesses, you can focus on improving those specific areas before the actual test.

• Take time to analyze each mistake and note the specific concept you struggled with.
• Work on additional problems related to your weaknesses to reinforce your understanding.
• Ask for help from a teacher or tutor if you’re unsure about the reasoning behind a mistake.

5. Stay Calm and Confident During the Test

On test day, it’s crucial to maintain a calm and focused mindset. Anxiety can cloud your judgment and cause you to make simple errors. Before starting, take a deep breath and remind yourself that you’re well-prepared. Trust in the work you’ve put in, and approach the test with confidence. If you get stuck on a question, move on and come back to it later with a fresh perspective.

• Read through all instructions carefully before beginning.
• Allocate time wisely for each section, ensuring you leave no question unanswered.
• Take a brief mental break if needed to keep your mind clear and sharp.

By following these strategies and dedicating time to practice, you’ll not only boost your confidence but also your ability to solve problems effectively under time pressure. With consistent effort and a positive approach, acing the test will be well within your reach.

How to Stay Confident During the Test

Maintaining confidence throughout a challenging assessment is crucial for optimal performance. The ability to stay composed under pressure allows you to think clearly, solve problems efficiently, and make the best use of your time. Confidence isn’t just about knowing the material; it also involves managing stress, maintaining a positive mindset, and staying focused. Below are some effective strategies to help you stay confident during the test.

1. Prepare Thoroughly in Advance

Confidence begins long before the test day. The more prepared you are, the more assured you’ll feel when you face the questions. Create a study plan that covers all the topics you need to review, and break it into manageable chunks. Consistently practicing problems will help reinforce your understanding and build self-assurance in your abilities.

• Set aside dedicated time for focused study sessions.
• Review past problems to get familiar with the question formats.
• Identify areas where you feel less confident and target them in your review.

2. Practice Stress-Relief Techniques

Managing stress during the test is essential for maintaining clarity and concentration. Simple breathing exercises, mindfulness techniques, or stretching can help calm your nerves and refocus your mind. Before the test, practice these stress-relief techniques so they become second nature when you’re in the testing environment.

• Take slow, deep breaths to calm your nerves.
• Visualize success by imagining yourself solving problems confidently.
• Focus on the present moment, avoiding distractions or anxious thoughts about outcomes.

3. Trust Your Preparation

When you’ve put in the work, trust that your preparation will carry you through. Often, self-doubt creeps in when you don’t give yourself credit for the effort you’ve invested. Remember that you’ve reviewed the material, practiced problem-solving, and taken steps to ensure you’re ready. Approach each question with the mindset that you know the material and are capable of solving it.

• Remind yourself of the effort you’ve put into studying.
• Focus on solving one question at a time rather than worrying about the whole test.
• Keep a positive attitude and stay focused on what you know, rather than what you don’t.

By using these strategies, you can stay calm, composed, and confident throughout the test. Confidence isn’t about perfection–it’s about believing in your ability to work through challenges and do your best.