Pre Algebra with Pizzazz Answer Key for Page 188

When tackling mathematical problems, having the right tools to check your work is essential. By reviewing solutions and understanding the thought process behind them, learners can gain a deeper insight into complex concepts and strengthen their skills. This guide offers an organized approach to solving and verifying exercises, providing a foundation for success in mathematics.
Throughout this section, students will find a step-by-step breakdown of exercises, highlighting crucial principles and common pitfalls. The goal is to equip learners with the strategies needed to build confidence and improve problem-solving efficiency. Mastering these methods will not only prepare students for future challenges but also encourage a lasting understanding of core mathematical techniques.
Pre Algebra with Pizzazz Answer Key Overview

Understanding the solutions to mathematical exercises is a critical part of the learning process. This section provides a structured approach to verifying your work and grasping the underlying principles behind each problem. By breaking down the methods used in solving each exercise, students can identify effective strategies and improve their problem-solving skills.
The provided material offers a comprehensive guide to the types of problems encountered, focusing on essential operations and techniques. It’s designed not only to assist in checking answers but also to encourage a deeper understanding of the mathematical concepts involved. Reviewing these solutions allows learners to recognize patterns and avoid common mistakes, ensuring more accurate and efficient results in future exercises.
Understanding the Purpose of Answer Keys
Answer guides play a vital role in the learning process by helping students verify their work and comprehend the methods used in solving various exercises. These resources serve as a reference point to ensure accuracy and to provide insight into the correct approach for each problem. By examining these solutions, learners can refine their problem-solving techniques and build confidence in their abilities.
Here are some key reasons why such guides are essential:
- Clarify Concepts: Answer guides offer clear examples of how to approach and solve specific problems, reinforcing understanding of core concepts.
- Correct Mistakes: Students can identify where they went wrong and learn how to avoid similar errors in future exercises.
- Enhance Problem-Solving Skills: By reviewing the steps taken to arrive at the solution, learners can improve their overall analytical thinking and methodical approach.
- Boost Confidence: Knowing the correct methods and verifying answers strengthens a student’s confidence and reduces anxiety around solving complex problems.
Ultimately, these guides act as tools for reinforcing and expanding a student’s knowledge, offering a clear path towards mastering mathematical exercises. They provide not only the right answers but also the reasoning behind them, which is crucial for long-term learning and success.
How to Use Answer Key Effectively
Having a solution guide can be a powerful tool for mastering mathematical exercises. However, it’s important to use it in a way that enhances understanding rather than just confirming answers. The guide should be viewed as a learning resource, not just a quick reference. By following a few key steps, students can maximize the benefit of these resources and improve their skills.
Step-by-Step Review
When using the guide, don’t just focus on the final result. Take the time to go through each step carefully. This will help you understand the logic and techniques involved in solving the problem. If you make a mistake, refer back to the guide to see where your reasoning diverged and use it to correct your approach.
Practice After Verification
Once you’ve reviewed the solution and understood the correct method, try similar problems on your own. This practice will solidify your grasp of the material and build your problem-solving ability. Over time, the more you use the guide to check your work, the more intuitive the process will become, and the less reliant you will be on external resources.
Key Topics Covered in Page 188
This section of the exercises focuses on foundational concepts that are essential for building a strong mathematical understanding. It covers various problem types and approaches, helping students develop a versatile skill set for tackling more complex tasks. By working through these topics, learners can gain a deeper insight into the fundamental operations and strategies that form the basis of mathematical reasoning.
Among the main themes explored in this section are:
- Basic Arithmetic Operations: Emphasis on addition, subtraction, multiplication, and division, and how to apply them in different contexts.
- Fractions and Decimals: Understanding how to manipulate fractions and decimals, and convert between them.
- Understanding Word Problems: Techniques for breaking down and solving problems presented in written form, enhancing comprehension skills.
- Order of Operations: The importance of following the correct sequence of steps to solve complex expressions and equations.
Each of these topics provides essential building blocks that will support further study in mathematics. By mastering these areas, students can move confidently into more advanced material, knowing they have a solid foundation to build upon.
Common Mistakes in Pre Algebra
Mathematical exercises can often lead to errors that stem from misunderstandings or careless mistakes. These errors can sometimes be difficult to spot, especially when the solution seems straightforward. Recognizing and addressing common mistakes is crucial for improving accuracy and building confidence in solving problems. By understanding where mistakes typically occur, students can develop strategies to avoid them in the future.
Some of the most frequent errors include:
- Misapplying the Order of Operations: One of the most common pitfalls is failing to follow the correct sequence of steps, leading to incorrect results.
- Forgetting to Simplify: After solving a problem, students sometimes overlook simplifying expressions or fractions, which can lead to incomplete answers.
- Incorrectly Handling Negative Numbers: Errors often occur when adding or subtracting negative numbers, especially when dealing with multiple signs in an expression.
- Overlooking Key Information in Word Problems: In written problems, it’s easy to miss crucial details, which can result in misunderstanding the question and arriving at the wrong solution.
- Confusing Similar Concepts: Sometimes, students mix up operations or mathematical rules that seem similar, such as the difference between multiplying and dividing fractions.
By identifying these errors and understanding their causes, students can focus on improving their problem-solving techniques, making fewer mistakes, and ultimately achieving greater success in their studies.
Step-by-Step Solutions for Page 188
Breaking down complex problems into manageable steps is an essential skill in mathematics. By following a structured approach, students can tackle exercises with greater clarity and precision. This section will guide you through each problem systematically, providing a clear explanation of the methods used and the reasoning behind each step. The goal is to offer a roadmap that will help you understand how to approach similar tasks in the future.
Each solution is carefully explained in a sequence of actions, designed to demonstrate the logical progression needed to arrive at the correct result. Here’s how the process typically unfolds:
- Identify the Problem: Begin by reading the problem thoroughly to understand what is being asked.
- Break Down the Components: Separate the equation or expression into smaller, more manageable parts.
- Apply the Correct Operations: Follow the necessary mathematical rules to simplify and solve the expression step by step.
- Check for Errors: After reaching a solution, review each step to ensure accuracy and correct any mistakes if necessary.
- Final Answer: Once you are confident that all steps have been completed correctly, state the final result clearly.
By following these detailed steps for each exercise, learners can build a deeper understanding of how to approach mathematical problems efficiently and accurately.
Why Page 188 is Essential for Mastery
This section provides key exercises that help reinforce important mathematical principles. It serves as a crucial step in building a solid foundation, allowing students to gain confidence and proficiency in fundamental skills. The material here is designed to challenge learners while providing opportunities to practice and refine essential techniques. Mastery of these concepts is vital for progressing to more advanced topics and solving complex problems with ease.
Building Core Skills
By working through the exercises in this section, students can strengthen their understanding of core concepts that form the basis of all mathematical problem-solving. These exercises focus on practical application, ensuring that learners can apply their knowledge to real-world situations. The practice offered here is directly linked to success in future challenges, as the skills developed will be necessary for tackling more advanced material.
Preparing for Complex Concepts
Mastering the material in this section also prepares students for more difficult topics in the future. The problems are designed to gradually increase in complexity, which helps build critical thinking and problem-solving abilities. As students work through these exercises, they are developing the mental flexibility needed to handle new and unfamiliar challenges with confidence.
Tips for Solving Pre Algebra Problems
Succeeding in mathematical exercises requires a mix of strategy, practice, and attention to detail. While the problems may seem difficult at first, applying the right techniques can make them more manageable. This section provides key tips to help you approach and solve exercises more effectively, ensuring better results and improved problem-solving skills.
Start with the Basics: Always review the fundamental concepts before tackling more complex problems. Having a solid grasp of the basic operations and rules will make advanced tasks much easier. If necessary, refresh your memory on core principles before moving forward.
Break Problems Down: Don’t try to solve everything at once. Divide the problem into smaller, more manageable parts. Focus on solving each part step by step, which will make the overall process less overwhelming.
Double-Check Your Work: Mistakes can often be subtle, especially in multi-step problems. After completing a solution, review your steps to ensure that no errors were made in your calculations or reasoning. Checking your work is a crucial habit that can save time in the long run.
Use Visual Aids: Sometimes, drawing a diagram or writing out a table can help make a complex problem clearer. Visual aids can provide a different perspective and may make it easier to spot relationships between numbers or variables.
Practice Regularly: The more problems you solve, the more confident you will become. Regular practice not only reinforces what you’ve learned but also helps you recognize patterns and develop problem-solving strategies more naturally.
By following these tips, you’ll improve your ability to approach and solve problems efficiently, setting yourself up for success in more advanced material.
How to Improve Algebra Skills
Improving mathematical abilities requires consistent effort and the application of effective strategies. To truly enhance problem-solving skills, it’s essential to focus on both understanding the underlying concepts and practicing regularly. With the right approach, anyone can develop a deeper understanding of mathematical principles and become more confident in solving problems.
Master the Fundamentals
The foundation of all advanced concepts is built on a clear understanding of the basics. Make sure you are comfortable with essential operations, such as addition, subtraction, multiplication, and division. Also, focus on understanding how to work with fractions, decimals, and integers, as these are key building blocks for more complex tasks.
Practice Problem-Solving Techniques
Consistent practice is the key to improvement. Work through a variety of problems regularly to reinforce your skills. When solving each problem, take the time to carefully analyze the steps involved and learn from any mistakes you make. The more problems you solve, the more intuitive the process will become, and the more efficient you will be in handling challenges.
Stay Organized: Keep your work neat and clearly structured. Organize your steps, show all calculations, and check your work before moving on to the next task. This habit will help avoid simple mistakes and allow for easier review of your solutions.
Ask for Help When Needed: Don’t hesitate to reach out to teachers, tutors, or peers if you encounter difficulties. Getting clarification on confusing concepts will help you overcome challenges faster and deepen your understanding of the material.
By following these strategies and committing to regular practice, you can steadily improve your mathematical skills and build confidence in solving problems.
Understanding Problem Types in Pre Algebra
Mathematical exercises vary widely in structure and approach, requiring students to adapt different strategies to solve them. Understanding the different types of problems helps learners approach each one with the right mindset and techniques. Recognizing patterns in problem types allows for a more systematic and efficient solution process, making complex tasks seem less intimidating.
Here are some common problem types you will encounter:
- Simple Equations: Problems where you solve for an unknown variable using basic arithmetic operations.
- Word Problems: These require translating real-world situations into mathematical expressions and solving them accordingly.
- Fraction Operations: Problems that involve adding, subtracting, multiplying, or dividing fractions.
- Integer Problems: Exercises that require operations with positive and negative whole numbers.
- Multi-Step Problems: More complex problems that require several steps to arrive at the solution.
Understanding the structure of these problems is essential. Each problem type may have specific rules or strategies that make solving it more efficient. By identifying the problem type early on, students can apply the most suitable methods and work through problems with greater ease.
Solving Word Problems in Pre Algebra
Word problems often present a challenge due to their need for translating real-world situations into mathematical expressions. Unlike straightforward equations, these problems require careful reading and critical thinking to extract the necessary information and determine the best approach. Mastering this skill is essential for applying mathematical knowledge to practical scenarios.
Breaking Down the Problem

The first step in solving a word problem is to read the question thoroughly. Pay attention to the details provided and highlight important numbers or conditions. Identify what the problem is asking you to find, whether it’s a specific value or a relationship between different variables. This will give you a clear direction for solving the problem.
Setting Up the Equation
Once you’ve identified the relevant information, the next step is to translate it into a mathematical expression or equation. Start by assigning variables to unknowns, then use the information given in the problem to create an equation that represents the situation. After setting up the equation, proceed with solving it step by step, making sure to follow the correct operations to find the solution.
By practicing these strategies and taking a systematic approach, you’ll be able to tackle word problems more confidently and effectively.
Understanding Mathematical Operations Clearly

To successfully solve mathematical problems, it’s crucial to have a clear understanding of the basic operations that underpin most exercises. These operations form the foundation of more complex concepts, and knowing when and how to apply them is key to finding accurate solutions. Whether it’s simple addition or more advanced operations like exponentiation, each step requires careful attention to detail.
Mathematical operations include addition, subtraction, multiplication, division, and more. Understanding the properties and rules governing these operations helps students approach problems confidently and accurately. Here’s a quick overview of how these operations interact:
| Operation | Symbol | Example | Result |
|---|---|---|---|
| Addition | + | 5 + 3 | 8 |
| Subtraction | – | 7 – 4 | 3 |
| Multiplication | * | 6 * 2 | 12 |
| Division | / | 8 / 2 | 4 |
| Exponentiation | ^ | 3^2 | 9 |
Understanding how these operations work individually and together allows you to break down complex problems into simpler steps, making it easier to arrive at the correct solution. Mastery of these fundamental operations is the key to tackling more advanced mathematical challenges.
How Answer Keys Aid Learning Algebra

Answer guides play a significant role in enhancing the learning process by providing students with a reliable resource for self-assessment and correction. By offering step-by-step solutions, these tools help learners understand where they might have gone wrong and how to improve their approach. Instead of simply presenting the final answer, they focus on the process, helping students grasp the underlying concepts more effectively.
Here’s how these guides can be particularly helpful in mastering mathematical concepts:
- Self-Assessment: Answer guides allow learners to compare their work with the correct solutions, identifying any mistakes or misunderstandings.
- Clarification of Steps: They often break down complex problems into smaller, more manageable steps, giving students insight into the logic behind each solution.
- Building Confidence: By confirming that their approach is correct or highlighting areas that need improvement, students can build confidence in their abilities.
- Promoting Independent Learning: With a clear reference, learners can work through problems independently, using the guide to verify their answers and refine their techniques.
- Reinforcing Concepts: Repeatedly referencing the guide helps reinforce essential techniques and reinforces problem-solving strategies.
Incorporating answer guides into study routines can transform the learning experience, making it more interactive and supportive. By using these resources effectively, students can improve both their understanding and performance in mathematics.
Using the Answer Key for Practice
Practicing mathematical problems is essential for mastering key concepts, and using a solution guide can significantly enhance the effectiveness of this practice. While working through exercises, having access to a solution reference helps ensure that students are on the right track. It not only allows for quick validation of answers but also provides valuable insights into the correct problem-solving methods.
Here are a few ways to effectively use a solution guide for practice:
| Strategy | How It Helps |
|---|---|
| Compare Solutions | After solving a problem, check your solution against the guide to ensure accuracy and identify areas of improvement. |
| Break Down Steps | Study the step-by-step breakdown in the guide to understand the thought process behind the solution, reinforcing key techniques. |
| Work Backwards | Start with the solution and reverse-engineer the steps to improve your problem-solving strategies. |
| Practice Similar Problems | Use the solutions to identify common patterns, then apply those patterns to similar problems for more practice. |
| Self-Correction | If you make a mistake, use the guide to pinpoint where the error occurred, then correct your approach accordingly. |
By incorporating these strategies into your study routine, you can enhance your problem-solving skills, identify weaknesses, and build greater confidence in your mathematical abilities. The solution guide becomes a powerful tool for refining techniques and deepening understanding.
Why Accuracy is Crucial in Algebra
In mathematics, precision is essential. A single mistake in calculation or misinterpretation of a problem can lead to incorrect conclusions, which may affect the entire solution. Mastering the ability to work accurately not only ensures correct answers but also strengthens your understanding of concepts and logical reasoning. Accuracy is the foundation of building more complex skills and applying mathematics to real-life scenarios.
Consequences of Inaccurate Solutions
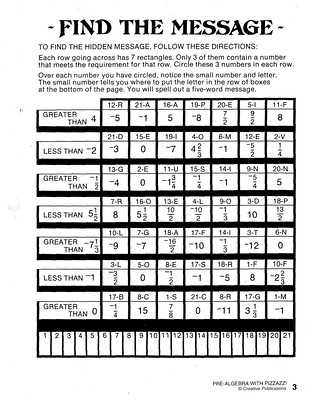
Even small errors can have a significant impact on the outcome of a mathematical problem. Here are some reasons why maintaining accuracy is crucial:
| Impact of Inaccuracy | Explanation |
|---|---|
| Incorrect Final Answer | A minor mistake in calculation can lead to an entirely wrong result, making the solution invalid. |
| Confusion in Concepts | Inaccurate solutions can confuse underlying concepts, making it harder to understand the next set of problems. |
| Loss of Confidence | Frequent errors can lead to a lack of confidence in one’s ability, making future problems seem more daunting. |
| Inability to Build on Skills | If foundational skills are incorrect, it becomes difficult to progress to more advanced topics and techniques. |
Maintaining Accuracy
To avoid errors, it’s essential to double-check your work, ensure that you fully understand the problem, and apply the correct operations at every step. Keeping track of your calculations and reviewing each step ensures that your solution is accurate and that your skills continue to improve.
How to Avoid Common Algebra Errors

Mathematical problems often seem straightforward, but small mistakes can lead to significant errors in your solutions. To succeed in solving equations and problems, it’s important to recognize and avoid the common pitfalls that can disrupt your progress. By understanding these common mistakes and implementing strategies to correct them, you can improve both the accuracy and efficiency of your problem-solving skills.
Common Mistakes to Avoid
Here are some of the most frequent errors encountered when solving mathematical problems and how to avoid them:
- Forgetting to Apply the Order of Operations: The order of operations is essential to getting the correct result. Always follow PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) to avoid mistakes.
- Incorrectly Distributing Multiplication: Make sure that when distributing a number across parentheses, each term inside the parentheses is multiplied correctly. For example, in 3(x + 4), multiply 3 by both x and 4.
- Sign Errors: Pay close attention to positive and negative signs. A simple mistake like -5 + 3 = 2 instead of -2 can change the entire outcome of the problem.
- Misunderstanding Variables: Be careful when substituting values for variables. Ensure that each variable is correctly assigned its corresponding number to avoid confusion.
- Skipping Steps: Always show your work and take each step methodically. Skipping steps can lead to overlooking a crucial detail that could affect the solution.
Tips for Minimizing Mistakes

By adopting the following strategies, you can minimize the chances of making common mistakes:
- Double-check your work: Always review your solutions to catch any mistakes before finalizing your answer.
- Practice consistently: The more you practice, the more familiar you become with common patterns and problem-solving techniques.
- Break down complex problems: If a problem feels overwhelming, break it down into smaller, more manageable parts.
- Ask for help when needed: Don’t hesitate to ask a teacher, tutor, or peer for clarification if you’re unsure about a concept or step in the process.
By being mindful of these errors and following these tips, you can greatly reduce the risk of making common mistakes and improve your overall problem-solving ability.