Similar Shapes Exam Questions and Answers

In geometry, recognizing when two figures share a consistent pattern can simplify complex problems. This concept is crucial for solving various types of problems related to scale, size, and measurement. By grasping how different forms relate to each other, you can develop a stronger foundation for tackling geometric challenges with confidence.

Throughout this guide, we will explore how to approach tasks involving proportionality, how to recognize when figures are proportionally related, and how to apply these principles effectively. Whether dealing with triangles, quadrilaterals, or other polygons, mastering these relationships can significantly improve your problem-solving skills.

Key techniques like comparing corresponding angles, sides, and applying ratios play a pivotal role in understanding the overall structure of related forms. By focusing on these methods, you will be better equipped to analyze various geometric scenarios and find accurate solutions quickly.

Geometric Proportions and Problem Solving

When working with geometric figures that share proportional relationships, it’s essential to understand how to correctly apply mathematical principles to determine their connection. This section covers a variety of exercises aimed at helping you identify when two figures maintain consistent ratios of side lengths and angles, providing an essential skill set for solving more advanced problems.

By analyzing the conditions under which two forms are related, you can develop a structured approach to tackle various tasks. This includes understanding the role of scale factors, corresponding sides, and angle measures in ensuring the integrity of your solution. With each example, the goal is to refine your ability to recognize patterns and apply appropriate strategies efficiently.

Practice problems are designed to test your knowledge, pushing you to apply the techniques you’ve learned. Whether dealing with basic tasks or more intricate geometric relationships, these problems provide a diverse set of challenges to strengthen your overall grasp of the topic. By regularly practicing, you’ll be well-prepared for more complex scenarios and able to solve them with ease.

Understanding Similarity in Geometry

In geometry, it is essential to recognize when two figures are related in a way that their proportions are consistent. This principle allows you to solve a wide range of problems by comparing the measurements of corresponding parts of the figures. Grasping the concept of proportionality helps in identifying when shapes can be considered as scaled versions of each other without distortion.

To truly understand this relationship, it’s important to focus on the following key concepts:

• Corresponding Angles: The angles of two figures that match each other in position.
• Proportional Sides: The lengths of sides that are in the same relative position in both figures.
• Scale Factor: The constant ratio by which one figure is scaled to form the other.

Once these basic ideas are clear, you can begin applying them to more complex problems. By examining the proportions of side lengths and the equality of corresponding angles, you can easily determine if two figures are related in this way. These steps are crucial when solving tasks that involve figures of different sizes but share the same shape or form.

Practical application of these concepts becomes easier with practice. Over time, recognizing and working with proportional relationships will become second nature, helping you approach geometric challenges with greater ease and accuracy.

Key Concepts for Identifying Similar Figures

To correctly identify when two geometric forms are proportionally related, understanding several fundamental concepts is crucial. These ideas allow you to compare different aspects of the figures, such as their side lengths, angles, and overall scale, to determine whether they share a consistent pattern of proportionality. Mastering these core principles will enhance your ability to analyze various figures and apply the correct methods for solving related problems.

Proportionality of Side Lengths

One of the most important aspects to look for is whether the corresponding sides of two figures maintain a consistent ratio. If the ratios of all corresponding sides are equal, then the two figures can be considered proportionally related. This is a primary indicator of their geometric relationship.

Figure 1 Side Lengths	Figure 2 Side Lengths	Ratio
4 cm	8 cm	2:1
6 cm	12 cm	2:1
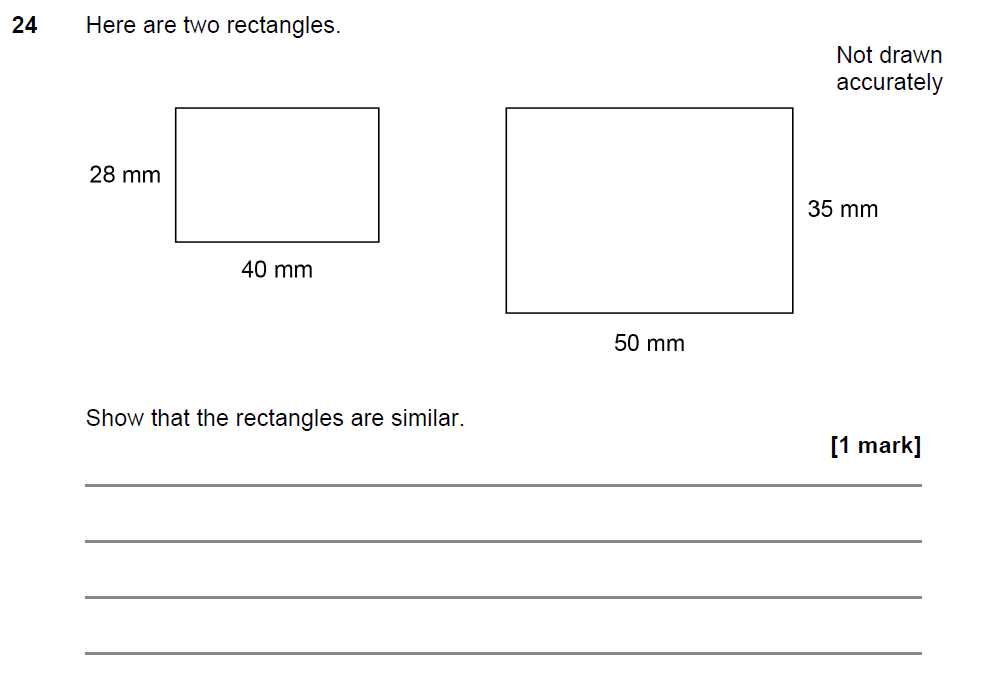
10 cm	20 cm	2:1

Equality of Corresponding Angles

Another crucial concept in identifying proportional relationships is checking for the equality of corresponding angles. If the angles in one figure match exactly with the angles in another, then the figures are related in a way that allows for proportional comparison of their sides.

By focusing on these two key principles–proportionality of sides and equality of angles–you can effectively identify when two figures are geometrically related. This understanding forms the foundation for solving a wide range of related problems and tasks.

How to Solve Geometric Proportionality Problems

Solving problems involving proportional figures requires a systematic approach that focuses on comparing relevant properties, such as side lengths, angles, and scale factors. By following a series of steps, you can effectively determine relationships between figures and apply the correct mathematical tools to find the solution. This section will guide you through the process of solving these types of problems with clarity and confidence.

Step 1: Identify Corresponding Parts

The first step is to identify which sides and angles in one figure correspond to the sides and angles in the other. This is crucial because the proportional relationships only hold between matching elements. Once you’ve established which parts match, you can move on to comparing them.

Step 2: Set Up Proportions

After identifying the corresponding elements, set up a proportion to compare the sides or angles. If the figures are proportionally related, the ratios of the corresponding sides will be equal. For example, if one figure has sides of 4 cm, 6 cm, and 8 cm, and the second figure has sides of 8 cm, 12 cm, and 16 cm, you can set up the proportion:

4/8 = 6/12 = 8/16

Once the proportion is set, you can solve for unknown values, such as side lengths or scale factors, by cross-multiplying and solving the resulting equation.

Tip: Always double-check that the corresponding sides are correctly identified before proceeding with calculations to avoid errors.

By consistently applying these steps, you’ll be able to solve a wide range of problems involving proportional relationships between figures with ease.

Types of Proportionality in Geometry

In geometry, there are different ways in which figures can be proportionally related. Understanding these various types allows you to identify and work with figures that share consistent ratios between their corresponding elements, such as angles and sides. These principles help establish the foundation for solving many geometric problems and enable a deeper understanding of geometric relationships.

Three main types of proportionality commonly arise when dealing with geometric forms:

• Angle-Angle (AA) Criterion: This type occurs when two figures have corresponding angles that are equal. If two pairs of angles are congruent, the figures are proportional, regardless of the size.
• Side-Angle-Side (SAS) Criterion: This occurs when two sides of one figure are proportional to two sides of another figure, and the included angle between these sides is equal in both figures.
• Side-Side-Side (SSS) Criterion: This type applies when the corresponding sides of two figures are proportional to each other. If the ratios of all three pairs of corresponding sides are equal, the figures are proportional.

By recognizing which type of proportionality applies to a given problem, you can quickly determine the relationships between the figures and proceed to solve the problem using the appropriate method. These criteria provide a structured approach to identifying and working with proportional figures in geometric contexts.

Practical Examples of Proportional Figures

Understanding proportional relationships between figures is not only essential for theoretical problems but also plays a crucial role in real-world applications. From architecture to design, identifying when objects share consistent proportions can help in various fields. By examining practical examples, we can see how these geometric principles are used to solve everyday problems.

One common example is the design of models or blueprints. Architects and engineers often work with scaled versions of buildings, vehicles, or machines. The original structure and its scaled-down model maintain the same proportions, ensuring that measurements can be accurately replicated in smaller sizes.

Another example occurs in photography and image scaling. When adjusting the size of an image, whether for printing or digital use, maintaining proportionality is key. If an image is resized incorrectly, it may become distorted, affecting its appearance. Keeping the original aspect ratio of the image ensures the proportions remain consistent.

In map-making, the concept of scaling is used to represent real-world distances in a manageable form. Maps use a scale factor to maintain the proportional relationship between real distances and their representation on paper. This allows for accurate navigation and measurement, despite the reduction in size.

By understanding and applying the principles of proportionality, we can solve various practical problems that arise in many different fields, making these concepts valuable tools for both academic and real-world scenarios.

Common Mistakes in Proportionality Problems

When solving problems involving proportional figures, it’s easy to make errors that can lead to incorrect conclusions. These mistakes often arise from misunderstanding the relationships between corresponding elements or misapplying mathematical rules. Recognizing and avoiding these common pitfalls can significantly improve your ability to solve such problems accurately.

One frequent mistake is incorrectly matching corresponding parts. It’s essential to identify which sides and angles correspond to each other before setting up ratios. A common error is to mix up corresponding sides or angles, which leads to incorrect proportions and ultimately wrong solutions.

Failing to maintain the correct ratio is another common issue. When comparing corresponding sides, it’s important to consistently apply the ratio between them. If you forget to scale one side properly or apply the wrong scale factor, the calculations will not yield the correct results. Additionally, some people may assume that the figures must be the same size, but proportionality applies regardless of size, as long as the corresponding elements maintain the same ratio.

Another mistake involves overlooking the angle conditions. In many problems, the equality of corresponding angles is a critical aspect of proportionality. Forgetting to check angle measures can lead to erroneous conclusions about the relationship between the figures.

Finally, misapplying theorems or formulas, such as the angle-angle (AA) or side-side-side (SSS) criteria, is a common problem. It’s essential to apply the correct theorem based on the information provided in the problem, and using the wrong method can result in incorrect answers.

By being aware of these common mistakes and taking the time to carefully check your work, you can avoid pitfalls and improve your accuracy when solving proportionality problems.

Proportions and Ratios in Proportional Figures

Understanding proportions and ratios is essential when working with figures that share consistent geometric relationships. These mathematical concepts allow us to compare corresponding parts of two or more figures and determine how their sizes relate to each other. Whether dealing with side lengths, areas, or volumes, the principles of proportionality provide the tools to analyze and solve various geometric problems effectively.

Proportional Relationships between Sides

One of the most fundamental concepts in geometry is the relationship between the corresponding sides of proportional figures. When two figures are proportionally related, the ratios of their corresponding sides are equal. This means that if one figure has a side of length 4 cm and the corresponding side of another figure has a length of 8 cm, the ratio of these sides is 1:2. If the figures are scaled by the same factor, all corresponding side lengths will maintain the same ratio.

To work with these ratios, it’s important to set up the proportion correctly. For example, if you’re given the lengths of two sides from each figure, you can use cross-multiplication to solve for an unknown side. Here’s an example:

4 cm / 8 cm = 6 cm / x

Cross-multiplying gives:

4 * x = 8 * 6

x = 48 / 4

x = 12 cm

Applying Ratios to Areas and Volumes

When working with areas and volumes, the concept of proportionality extends to squared and cubed relationships. For example, when comparing the areas of two proportional figures, the ratio of their areas is the square of the ratio of their corresponding sides. Similarly, when comparing volumes, the ratio of the volumes is the cube of the ratio of the corresponding sides.

For instance, if the ratio of the sides of two cubes is 2:3, the ratio of their areas will be:

2²:3² = 4:9

And the ratio of their volumes will be:

2³:3³ = 8:27

Understanding how these ratios work for areas and volumes is vital in many practical applications, such as architecture, engineering, and design.

How to Use Scale Factor Effectively

Using the scale factor correctly is essential when working with figures that are proportional to each other. The scale factor defines the ratio between the corresponding elements of two objects, and applying it accurately allows you to make calculations involving side lengths, areas, and even volumes. Knowing how to use the scale factor effectively is crucial for solving problems in both academic and real-world contexts, such as in design, architecture, and engineering.

Understanding the Scale Factor

The scale factor is simply the ratio of any two corresponding linear measurements in proportional figures. If you are scaling up or down a figure, the scale factor tells you how much larger or smaller the new figure will be compared to the original. For example, if the scale factor is 2, each side of the scaled figure will be twice the length of the original figure. Conversely, if the scale factor is 0.5, each side will be half the length of the original.

Example: If a rectangle has side lengths of 4 cm and 6 cm, and you apply a scale factor of 3, the new rectangle will have sides of 12 cm and 18 cm.

Applying the Scale Factor in Different Contexts

Once you understand the scale factor, you can use it to solve various problems. For instance, to calculate the area of a scaled figure, you square the scale factor. This is because area is a two-dimensional measurement, and scaling each side by a factor results in the area being scaled by the square of the scale factor.

Example: If the scale factor for two similar figures is 3, the area of the scaled figure will be 3² = 9 times larger than the original.

Similarly, for volumes (three-dimensional measurements), the scale factor is cubed. This means that the volume of the scaled figure will increase by the cube of the scale factor.

Example: A scale factor of 2 will increase the volume by 2³ = 8 times.

By mastering the use of the scale factor, you can accurately solve problems involving proportional relationships in both two and three dimensions, making it a valuable tool in various mathematical and practical applications.

Solving Word Problems Involving Proportional Figures

Word problems that involve proportional relationships can often seem challenging at first, but with the right approach, they become manageable. The key to solving these problems is identifying the corresponding parts of the figures and setting up the correct relationships between them. By understanding how proportions work, you can break down the problem into smaller, solvable steps and find the required values efficiently.

When you are faced with a word problem, the first step is to read the problem carefully and identify the figures involved. Look for clues in the description that suggest the objects are related proportionally, such as identical angles or proportional side lengths. Once you recognize this relationship, you can apply the appropriate mathematical methods to solve for unknown quantities.

Next, write down any known measurements and use them to set up a proportion. For example, if you are asked to find the length of a missing side in a figure, and you know the lengths of corresponding sides in another, proportional figure, you can use a ratio to solve for the unknown side. Always double-check that you are comparing the correct parts of the figures, as matching sides or angles is crucial for getting the right solution.

Finally, after setting up your proportion, use cross-multiplication or other solving techniques to find the missing value. If the problem involves other quantities like area or volume, remember to apply the appropriate power of the scale factor, whether it’s squaring for area or cubing for volume.

By following these steps systematically, you can solve word problems involving proportional figures with confidence and accuracy. With practice, these types of problems will become easier to understand and solve, and you will develop a deeper understanding of the relationships between different types of measurements.

Applications of Proportional Figures in Real Life

Proportional relationships are not just abstract concepts confined to textbooks; they play a significant role in various practical fields. From architecture to technology, understanding how different parts of an object relate proportionally to one another allows professionals to create designs, models, and solutions that are both functional and efficient. These concepts are applied in numerous industries where scaling and measurement are key to achieving accuracy and precision.

Architecture and Design

In architecture, the use of proportional relationships is essential for scaling designs from blueprints to physical structures. Architects often use proportionality to create aesthetically pleasing and functional buildings, ensuring that different sections of a structure are in harmony with one another. For example, when designing a building, the dimensions of windows, doors, and rooms may be based on proportional relationships that help maintain balance and symmetry throughout the design.

Additionally, scaling models of buildings or products often involves these proportional principles. Architects and designers use smaller models to visualize large structures, and the same proportionality is applied to ensure that every part of the model corresponds to the actual dimensions in real life.

Manufacturing and Engineering

In the manufacturing industry, scaling up or down products based on proportional principles is crucial. Whether it’s designing mechanical parts, consumer goods, or vehicles, engineers use proportionality to ensure that parts fit together correctly when scaled. For instance, when creating a model of a car for testing, engineers use proportional measurements to ensure that all parts function similarly to the real-size model.

In technology, these principles also apply when designing screens, such as those for phones and TVs, where elements like pixels and resolution must follow specific ratios to maintain visual quality across different sizes. The same idea extends to 3D printing, where models are scaled proportionally to create physical objects based on digital designs.

From art to science, understanding proportional relationships is a powerful tool that shapes many of the designs and solutions we use daily, highlighting the real-world applications of these mathematical concepts.

Geometric Proofs for Proportional Figures

In geometry, proving that two figures are proportionally related involves demonstrating that their corresponding angles and sides follow specific mathematical relationships. A variety of geometric theorems and properties can be used to establish these proportional relationships. This section explores the fundamental principles and common methods used in proofs related to proportional figures.

Key Concepts for Proofs

When proving proportionality between figures, it’s essential to use several core concepts. These concepts help establish the conditions under which two objects are proportional, and they often involve using congruent angles, corresponding sides, and ratios. Here are some of the key tools used in geometric proofs:

• Angle-Angle (AA) Similarity Criterion: If two angles of one figure are congruent to two angles of another figure, then the figures are proportional.
• Side-Angle-Side (SAS) Similarity Criterion: If two sides of one figure are proportional to two sides of another figure, and the included angle is congruent, the figures are proportional.
• Side-Side-Side (SSS) Similarity Criterion: If the corresponding sides of two figures are proportional, the figures are proportional.

Applying Proofs in Real Problems

Once the key criteria are established, they can be applied to solve real geometric problems. Here’s how to approach such proofs:

1. Identify Corresponding Parts: First, determine which sides and angles in the two figures correspond to each other.
2. Check for Congruent Angles: Ensure that the corresponding angles in the figures are either directly given or can be inferred.
3. Apply the Proportionality Criteria: Use the appropriate similarity criterion to establish the proportionality of the figures. This could involve showing that the corresponding sides have the same ratio or that angles are congruent.
4. Use Algebraic Techniques: If necessary, use algebra to solve for unknown values in the proportional relationships.

By following these steps, one can successfully prove the proportionality of two figures and solve related geometric problems with confidence. These proofs are essential tools in various fields of mathematics, science, and engineering, where understanding the relationships between objects is key to solving complex problems.

Using the AA Criterion for Proportional Figures

The Angle-Angle (AA) criterion is one of the simplest and most frequently used methods to establish proportionality between two figures. This criterion states that if two angles of one figure are congruent to two angles of another figure, then the figures are proportional, meaning their corresponding sides are in the same ratio. It is a valuable tool in geometric proofs, particularly when analyzing figures that share common angles but may differ in size.

To apply the AA criterion, the first step is identifying the corresponding angles between the two figures. These angles should either be directly given or inferred using other geometric properties, such as parallel lines or transversals. Once the angles are established, it can be concluded that the figures are proportional, regardless of their actual size or scale.

Conditions for Applying the AA Criterion

To correctly use the AA criterion, the following conditions must be met:

• Two corresponding angles in each figure must be congruent: The figures should share at least two angles that are exactly the same in measure.
• The figures must be in the same orientation: The relative positions of the corresponding angles should be consistent to ensure correct comparisons.

Example of Using the AA Criterion

Consider two triangles where we know that one pair of corresponding angles are congruent, and the second pair of angles are also congruent. According to the AA criterion, these two triangles will be proportional. Let’s examine a simple example:

Figure	Angle 1	Angle 2	Conclusion
Triangle 1	30°	60°	Proportional to Triangle 2
Triangle 2	30°	60°	Proportional to Triangle 1

In this example, since the corresponding angles in both triangles are congruent (30° and 60°), we can conclude that the triangles are proportional, and their corresponding sides will be in a constant ratio. This method is often used in various geometric problems and real-world applications, such as in architecture and design, where similar structures need to be scaled based on specific angular relationships.

Understanding Corresponding Angles and Sides

In geometry, analyzing the relationships between different parts of figures is crucial for solving many problems. When two figures have specific proportional properties, we often look at the matching angles and sides to determine how they relate to each other. Corresponding angles are those that occupy the same relative position in two different figures, and corresponding sides are the sides that are in the same relative position. Understanding how these elements interact can help in solving problems involving scaling or transforming figures.

To identify corresponding angles and sides, it’s important to recognize the structure of the figures involved. For example, in two triangles, the angles that are in the same location (e.g., top-left) are called corresponding angles, while the sides that are opposite to those angles are called corresponding sides. When these angles and sides maintain specific ratios or congruence, the figures can be considered proportional or congruent depending on the context.

Corresponding Angles

Corresponding angles are angles that are in the same position in two similar figures. These angles are congruent, meaning they have the same measure. The concept of corresponding angles is frequently used when dealing with parallel lines and transversals, as they are formed by the intersection of these lines. Here are key points about corresponding angles:

• Position: They occupy the same relative position in both figures.
• Congruency: Corresponding angles are always congruent in proportional figures.
• Parallel Lines: Corresponding angles are often identified when a transversal crosses two parallel lines.

Corresponding Sides

Corresponding sides are the sides that are in the same relative position in two figures. If two figures are proportional, their corresponding sides will have a constant ratio. Here are some important notes about corresponding sides:

• Proportionality: In similar figures, corresponding sides are proportional, meaning the ratio of one side to another is the same across all pairs of corresponding sides.
• Scaling: Corresponding sides may differ in length, but the ratio between them remains constant.
• Positioning: Like corresponding angles, corresponding sides match up in the same relative positions in different figures.

By identifying the corresponding angles and sides between two figures, you can use these relationships to solve problems involving scaling, similarity, and congruency. For example, if the corresponding angles are known to be congruent and the corresponding sides are proportional, you can calculate unknown dimensions or verify if two figures are proportional. These concepts form the foundation for many geometric proofs and real-world applications, such as architectural design and mapping.

Exploring the Role of Triangles in Similarity

Triangles play a fundamental role in understanding proportional relationships in geometry. Their properties are often used to explore how different figures relate to one another in terms of size, angles, and proportions. The concept of similarity, when applied to triangles, involves comparing corresponding angles and sides to establish how two triangles might be related in scale without altering their shape.

When working with triangles, it is crucial to identify certain key elements that help determine the proportionality between two triangles. These elements include the angles, which should be congruent, and the sides, which should have a consistent ratio. Triangular similarity is often the first concept introduced when learning about geometric transformations and helps build a foundation for more complex concepts in mathematics.

To recognize whether two triangles are proportionally related, there are several criteria that can be applied. These criteria focus on matching angles and sides in specific ways that allow one triangle to be transformed into another by scaling. Let’s explore how these criteria work:

Criteria for Triangular Proportionality

There are several established rules that help in determining whether two triangles are proportional. Each rule provides a method for comparing the elements of the triangles, ensuring that they meet specific conditions:

• AA Criterion: If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar. This is often the most straightforward method to prove proportionality between two triangles.
• SAS Criterion: If two sides of one triangle are in the same proportion to two sides of another triangle, and the included angles between these sides are congruent, the triangles are similar.
• SSS Criterion: If the corresponding sides of two triangles are in proportion, the triangles are similar. This method ensures that all three sides of one triangle have the same ratio as the corresponding sides of another triangle.

Applications of Triangular Proportionality

In practical terms, understanding how triangles relate to one another through proportionality has numerous applications. Some of the most common uses include:

• Architecture: Architects frequently use triangular proportions to design structures that are scaled versions of one another while maintaining the same proportions.
• Mapping: In cartography, triangles are used to represent regions on a smaller scale while preserving the angles and proportions of the real-world features they represent.
• Photography: Photographers use triangular relationships to adjust the scale of images while keeping the dimensions proportionally accurate, often employing similar principles when working with camera angles and object positioning.

By understanding the principles that govern triangular proportionality, it becomes easier to apply this knowledge to real-world problems. Whether it’s for scaling designs, analyzing geometric shapes, or solving mathematical problems, the role of triangles in proportional relationships is key to mastering geometric concepts.

Practice Questions on Similarity

Practicing with problems related to proportional figures is essential for gaining a deeper understanding of the underlying concepts. These types of exercises help to reinforce key principles such as scaling, comparing angles, and determining proportional relationships between corresponding sides. Below are several practice scenarios designed to test your ability to apply these concepts in different contexts.

Each problem requires careful analysis of the given figures and the relationships between them. By breaking down the information step-by-step, you can apply the appropriate criteria to identify how the figures relate to each other in terms of size and angles. Below are some example problems to help you practice:

Problem 1: Determine the Scale Factor

In the diagram, two triangles are presented. One is scaled up from the other. The smaller triangle has sides of 4 cm, 6 cm, and 8 cm, while the larger triangle has sides of 8 cm, 12 cm, and 16 cm. Find the scale factor between the two triangles.

• Step 1: Compare the corresponding sides.
• Step 2: Calculate the ratio of the sides.
• Step 3: Conclude the scale factor.

Problem 2: Proportionality of Areas

Two figures have the same proportions. The smaller figure has an area of 25 cm², and the larger one has an area of 100 cm². Find the ratio of their corresponding side lengths.

• Step 1: Find the square root of the ratio of the areas.
• Step 2: Calculate the ratio of the side lengths.
• Step 3: Confirm the proportionality of the side lengths.

Problem 3: Angle Comparison

In two polygons, the corresponding angles are congruent. The first polygon has sides of 5 cm, 7 cm, and 9 cm. The second polygon has sides of 10 cm, 14 cm, and 18 cm. Are the two polygons proportionally related? Justify your reasoning based on angle congruency and side ratios.

• Step 1: Verify the congruency of the angles.
• Step 2: Check the side ratios.
• Step 3: Determine if the figures are proportionally related.

Problem 4: Using the SSS Criterion

Two triangles have corresponding sides of 6 cm, 9 cm, and 12 cm in the first triangle, and 18 cm, 27 cm, and 36 cm in the second triangle. Are the two triangles proportional? Use the SSS criterion to justify your answer.

• Step 1: Check the side ratios.
• Step 2: Apply the SSS criterion for proportionality.
• Step 3: Conclude whether the triangles are proportional.

Problem 5: Real-Life Application

A photographer is using a scale model of a building for a photo shoot. The model’s dimensions are 1/10 of the real building’s dimensions. If the model has a height of 3 cm, what is the height of the actual building?

• Step 1: Determine the scale factor.
• Step 2: Multiply the model’s height by the scale factor.
• Step 3: Calculate the height of the actual building.

These practice problems are designed to improve your problem-solving skills in geometry, focusing on proportional relationships and scaling. By working through these exercises, you can better understand how to apply the concepts of proportionality in real-life and theoretical scenarios.

Tips for Exam Preparation on Similarity

Preparing for assessments that focus on proportional figures requires both conceptual understanding and practical problem-solving skills. A solid grasp of how to identify and apply proportionality rules will help you approach problems with confidence. In this section, we will explore essential strategies that will guide you in mastering the topics related to scaling, ratios, and geometric relationships. These tips are designed to streamline your study process and enhance your problem-solving abilities.

1. Master Key Concepts

Before attempting practice problems, ensure you understand the core principles of proportionality, such as how corresponding sides and angles relate in scaled figures. Review definitions and criteria like the AA criterion, SSS criterion, and the importance of proportional side lengths and angles. A strong foundation in these concepts is crucial for correctly solving any related problems.

2. Practice with Diverse Problems

Solving a variety of problems that involve proportional relationships between figures is one of the most effective ways to prepare. Start with simple examples and gradually tackle more complex scenarios that involve multiple steps. This will allow you to recognize patterns and gain the ability to apply different methods depending on the problem at hand.

3. Visualize the Figures

When dealing with figures, whether geometric or word problems, it’s helpful to sketch them out. This allows you to clearly identify corresponding sides, angles, and any scale factors. By drawing the figures, you can better understand their relationships and avoid confusion when it comes time to apply ratios or solve for unknown values.

4. Understand the Role of Scale Factor

Scale factor is a key element in comparing proportions. Make sure you are comfortable with how to calculate and use the scale factor in various contexts. Recognizing how the scale factor affects side lengths and areas will give you an edge when solving problems related to proportionality.

5. Focus on Word Problem Techniques

Word problems often require you to extract information from textual descriptions. Practice translating word problems into visual representations or equations, which will help you break down the problem logically. Focus on identifying the given values and determining what is being asked. Once you’ve identified the relationships, set up proportional equations to find the solution.

6. Review Common Pitfalls

Common mistakes in these problems involve confusing ratios of areas with ratios of sides or neglecting to check for congruent angles when applying certain criteria. Review these common pitfalls and practice identifying them in problems to avoid them during your assessment.

7. Use Practice Tests

Once you feel confident with the material, simulate test conditions by timing yourself on practice problems. This will help you develop time management skills and get comfortable working under pressure. In addition, reviewing your mistakes and understanding why you got a problem wrong is a great way to reinforce the material.

Tip	Description
Master Key Concepts	Understand the criteria for proportionality and the relationships between sides and angles.
Practice with Diverse Problems	Work through a range of problems to gain familiarity with different types of scenarios.
Visualize the Figures	Draw figures to better understand their relationships and solve the problem more clearly.
Understand the Role of Scale Factor	Learn how scale factors influence side lengths and areas in proportional figures.
Focus on Word Problem Techniques	Translate word problems into visual representations or equations for easier solution.
Review Common Pitfalls	Be aware of common mistakes, such as mixing up ratios of areas with side lengths.
Use Practice Tests	Test your skills under timed conditions to improve your speed and accuracy.

By following these tips and practicing regularly, you’ll be well-prepared to tackle problems involving proportionality in your assessment. Remember, understanding the underlying principles and practicing consistently are the keys to success in any topic related to geometric relationships.