Algebra 1 Module 1 Answers and Solutions

In the early stages of learning mathematical fundamentals, grasping the foundational ideas is essential for building stronger skills. This section aims to guide students through critical problem-solving techniques and methods to enhance their understanding. By focusing on basic operations and structure, learners can develop the tools needed for more complex challenges.
Breaking down problems and approaching them step by step is a key to success. Throughout this guide, students will find clear examples and solutions that illustrate the most efficient ways to tackle common exercises. Emphasis will be placed on reasoning and understanding the process, rather than just memorizing formulas.
With a solid foundation in these early topics, students can confidently advance to more intricate areas of study. This resource will help you connect the dots and strengthen your mathematical thinking for future learning.
Algebra 1 Module 1 Answers Overview

In this section, we will explore key concepts and solutions to common exercises found in the initial phase of the curriculum. The focus will be on fundamental operations, essential rules, and techniques that help build a strong mathematical foundation. By reviewing these solutions, learners will gain a clearer understanding of how to apply these principles to solve problems effectively.
We will cover a variety of topics, from solving basic equations to understanding essential concepts that are crucial for advancing in mathematics. Each exercise will be broken down to show the step-by-step process, offering insight into how to approach different problem types. Below is a table summarizing the primary areas covered and corresponding solutions.
| Topic | Key Concepts | Solution Approach |
|---|---|---|
| Basic Operations | Adding, subtracting, multiplying, and dividing numbers | Using simple arithmetic rules to combine terms |
| Working with Variables | Understanding the role of variables in equations | Isolating variables to find their values |
| Equations | Linear equations and solving for unknowns | Applying inverse operations to simplify expressions |
| Word Problems | Translating real-life scenarios into mathematical expressions | Breaking down the problem and solving step by step |
| Order of Operations | Understanding PEMDAS and its application | Following the correct sequence to simplify expressions |
By understanding and practicing these key areas, students will be better equipped to handle more complex challenges in later stages of their studies. These solutions serve as a solid foundation for continued mathematical learning and application.
Understanding Basic Algebraic Concepts
Mastering the core principles of mathematical operations is essential for solving problems efficiently. This section focuses on key ideas that serve as the building blocks for more advanced topics. A strong grasp of these foundational concepts enables learners to approach increasingly complex challenges with confidence and clarity.
Variables and Expressions
At the heart of solving problems lies the concept of variables–symbols that represent unknown values. These variables are used in expressions, which combine numbers, variables, and mathematical operations. Understanding how to manipulate these expressions is vital for solving equations and simplifying problems. The ability to identify and work with variables allows learners to translate real-world situations into mathematical language.
Equations and Solutions
Equations are statements that show the relationship between two expressions. To solve an equation, the goal is to find the value of the variable that makes the equation true. This involves isolating the variable through various operations. Developing a clear understanding of this process ensures accuracy when solving for unknowns and helps reinforce the logical thinking required for more complex tasks.
Key Skills in Algebra 1 Module 1
Developing strong problem-solving abilities is essential in the early stages of mathematical study. This section highlights the fundamental skills that are crucial for success in solving equations and simplifying expressions. Mastering these abilities provides a solid foundation for tackling more complex mathematical tasks in the future.
One of the key skills is the ability to manipulate expressions by applying basic operations, such as addition, subtraction, multiplication, and division. Learning to simplify and combine terms efficiently is vital for solving problems quickly and accurately. Another important skill is understanding the concept of balance when working with equations, which helps in isolating variables and finding solutions.
Additionally, proficiency in recognizing patterns and relationships between numbers allows students to solve word problems and apply mathematical reasoning to real-life scenarios. By practicing these essential skills, learners can enhance their overall problem-solving strategies and prepare for advanced concepts.
Step-by-Step Solutions for Exercises
To effectively solve mathematical problems, it is important to break them down into manageable steps. This section provides a detailed, step-by-step guide to solving common exercises, ensuring that each concept is fully understood. By following a structured approach, learners can gain clarity and confidence in their problem-solving abilities.
Each example will be explained progressively, starting from the initial equation or expression. The process will focus on isolating variables, simplifying terms, and applying the correct operations. By practicing this method, students will not only arrive at the correct solution but will also develop a deeper understanding of the logical sequence behind each step.
Through these step-by-step explanations, learners will be equipped with the necessary skills to tackle a wide variety of problems, building a strong foundation for more advanced topics in the future.
Common Mistakes in Module 1
When learning fundamental mathematical concepts, it is common to encounter mistakes that can hinder progress. Understanding and addressing these errors is crucial for improving accuracy and building confidence. In this section, we highlight some of the most frequent missteps and provide guidance on how to avoid them.
- Misunderstanding Operations: One of the most common errors is applying operations incorrectly. This often occurs when combining terms or solving for variables. For example, students may incorrectly add instead of subtract or misapply the distributive property.
- Forgetting to Simplify: Another frequent mistake is neglecting to simplify expressions fully. It’s easy to overlook combining like terms or reducing fractions, which can lead to incorrect solutions.
- Ignoring the Order of Operations: Failing to follow the correct sequence of operations (PEMDAS) is a typical error. Skipping steps or performing calculations out of order can result in wrong answers.
- Incorrectly Handling Negative Signs: Negative numbers can be tricky. Students sometimes make mistakes when multiplying or dividing negative values, or when dealing with subtraction.
- Not Checking Work: A simple yet crucial mistake is forgetting to verify solutions. Failing to double-check calculations often leads to minor but impactful errors.
By recognizing these common pitfalls and practicing the correct techniques, students can avoid these mistakes and improve their mathematical skills over time.
How to Approach Word Problems
Word problems are a key aspect of applying mathematical concepts to real-world situations. They can initially seem complex, but with the right strategy, they become easier to tackle. In this section, we will explore effective methods for translating a problem into a solvable equation and then walking through the steps to find the solution.
The first step in solving word problems is to carefully read the problem and identify the key information. It’s important to understand what is being asked and what data is provided. Once the problem is broken down, the next step is to translate the verbal description into a mathematical expression or equation. From there, solving the problem becomes a matter of applying the appropriate operations and solving for the unknowns.
| Step | Action | Example |
|---|---|---|
| 1 | Read and Understand | Identify the key details, such as numbers, relationships, and what the question is asking for. |
| 2 | Translate into Math | Convert the words into an equation using variables and operations. |
| 3 | Set up the Equation | Organize the information in a clear, solvable format. |
| 4 | Solve and Check | Perform calculations, then review the solution to ensure it makes sense. |
By following these steps, students can confidently approach word problems, ensuring they extract the necessary information and apply the correct mathematical methods to find the solution.
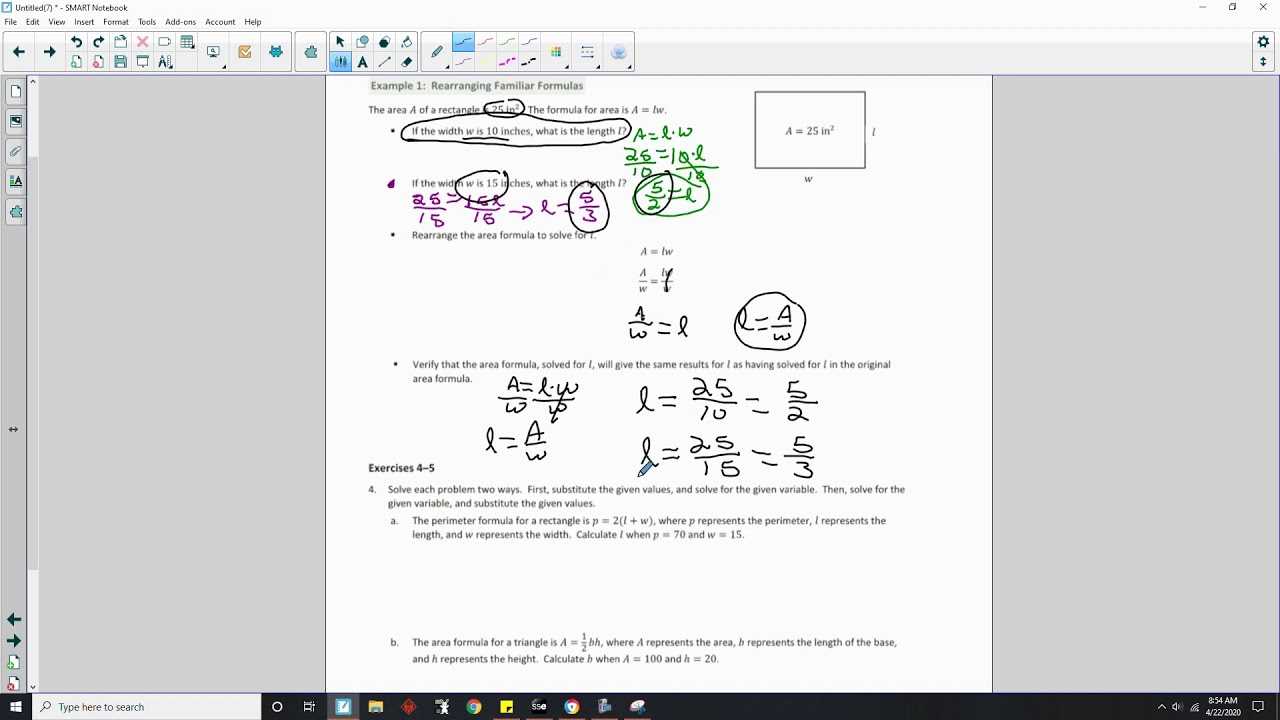
Solving Equations in Module 1
Solving equations is a fundamental skill in mathematics that involves finding the value of an unknown variable. This process is essential for many problem types, and mastering it early on sets the stage for solving more complex challenges. The goal is to manipulate the equation step by step to isolate the variable and determine its value.
The key to solving equations is to apply the correct operations to both sides of the equation while maintaining equality. This may involve adding, subtracting, multiplying, or dividing terms in a way that simplifies the expression. The key is to perform each step carefully and systematically to avoid errors and reach the correct solution.
Below are the general steps to follow when solving simple linear equations:
- Step 1: Simplify both sides of the equation if necessary.
- Step 2: Use inverse operations to move terms involving the variable to one side and constant terms to the other side.
- Step 3: Isolate the variable by performing the same operation on both sides of the equation.
- Step 4: Solve for the value of the variable.
- Step 5: Check the solution by substituting it back into the original equation.
By practicing these steps consistently, students can build a strong foundation in solving equations, which will be crucial as they progress in their studies.
Importance of Variables in Algebra
Variables play a crucial role in solving mathematical problems and represent unknown values that we aim to find. They provide the flexibility to express general relationships and solve for specific numbers, making them indispensable in various mathematical operations. Without variables, it would be impossible to write equations that describe real-world situations or complex mathematical relationships.
Understanding the significance of variables is vital because they allow for the creation of formulas, the representation of patterns, and the generalization of rules. In many problems, the variable is the unknown quantity we seek to solve, and identifying how to manipulate it effectively is key to finding the correct answer.
- Flexibility: Variables enable the expression of mathematical relationships that are not tied to a specific number, making them adaptable to different situations.
- Solving Problems: They serve as placeholders for unknown values, allowing for equations that can be solved through logical operations.
- Representing Relationships: Variables are essential in creating formulas that describe patterns, such as those found in geometry, finance, or science.
- Generalization: They allow us to write rules and equations that apply to many cases, rather than just a single instance.
By understanding the importance of variables, learners can approach a wide range of problems with the tools needed to solve them, whether they are working with simple expressions or more complex equations.
Practical Applications of Algebra 1
The concepts learned in early mathematics have wide-reaching applications that extend far beyond the classroom. While solving equations and manipulating expressions may seem abstract at first, these skills are essential for tackling real-world challenges. From budgeting personal finances to analyzing scientific data, the principles learned in this foundational level can be applied in numerous practical scenarios.
One of the key ways these concepts are used is in everyday problem solving. Whether calculating discounts during a shopping trip, determining the correct amount of paint for a room, or predicting future expenses, mathematical reasoning is a critical tool for making informed decisions. In fields like engineering, technology, and economics, the ability to translate real-life situations into mathematical terms is an indispensable skill.
Personal Finance and Budgeting
Understanding how to manage money involves basic mathematical skills, including creating budgets, calculating interest rates, and planning for savings. Whether it’s dividing a budget into categories or understanding how loans accumulate interest over time, mathematical reasoning helps individuals make sound financial choices.
Career Applications
Many careers require a solid grasp of mathematical principles. Fields such as architecture, computer science, and data analysis rely heavily on mathematical models and equations. The ability to solve problems using variables and equations is essential in these industries, as it helps professionals make predictions, solve technical issues, and optimize performance.
In conclusion, the practical applications of early mathematical concepts are vast and invaluable. They equip students with the tools they need to navigate and succeed in both personal and professional aspects of life.
Tips for Mastering Algebraic Expressions
Mastering the manipulation and simplification of expressions is a key skill in mathematics that lays the foundation for more complex problem-solving. By understanding how to handle variables, constants, and operations within an expression, students can tackle a wide range of problems with ease. Here are some essential tips to help you gain confidence and proficiency in working with mathematical expressions.
Understand the Basics
Before diving into more complex problems, it’s important to be comfortable with the basic components of an expression. These include variables, coefficients, and constants. Understanding how each part contributes to the overall equation will make it easier to manipulate and simplify expressions.
- Variables: Represent unknown values that we are solving for.
- Coefficients: Numbers that multiply the variables.
- Constants: Fixed numbers that are not affected by the variables.
Follow Order of Operations
One of the most important aspects of solving expressions is ensuring that you follow the correct order of operations. This order, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), ensures that you solve problems consistently and accurately.
- Parentheses: Always simplify expressions inside parentheses first.
- Exponents: Handle any exponents next.
- Multiplication and Division: Perform these operations from left to right.
- Addition and Subtraction: Finally, perform addition or subtraction from left to right.
By mastering these essential concepts and following the order of operations, you will develop a strong foundation for working with more advanced expressions and solving complex problems.
Strategies for Efficient Problem Solving
Effective problem-solving is a skill that can be developed through practice and applying the right strategies. Whether you’re tackling a simple equation or a more complex expression, having a structured approach can make a significant difference in both accuracy and speed. The key is to break down the problem into manageable steps, eliminate unnecessary complexity, and apply logical reasoning to find the solution.
Here are some strategies that can help improve your problem-solving efficiency:
| Strategy | Description |
|---|---|
| Understand the Problem | Before attempting to solve any problem, take time to fully understand the question. Identify known values and unknown variables. |
| Break It Down | Divide the problem into smaller, easier-to-manage parts. Solving one step at a time helps reduce mistakes and makes the process less overwhelming. |
| Use Visual Aids | Draw diagrams, charts, or tables to visualize relationships and organize information. This can often make the problem clearer. |
| Look for Patterns | Recognize common patterns that can simplify the problem. This could be through factoring, simplifying terms, or identifying symmetry in the equation. |
| Check Your Work | Always double-check your calculations and logic. A quick review can often help spot simple mistakes before finalizing your answer. |
By implementing these strategies, you can improve both your efficiency and accuracy when solving problems, ultimately helping you tackle even the most challenging questions with confidence.
Role of Integers in Algebraic Solutions
Integers play a crucial role in solving mathematical problems, particularly when working with equations and expressions. These whole numbers, whether positive or negative, help form the backbone of many equations and are essential in performing operations like addition, subtraction, multiplication, and division. Understanding how to work with integers effectively can significantly simplify the problem-solving process and lead to more accurate results.
Integers are used in a variety of ways, from representing values in real-world scenarios to simplifying complex equations. Their role is fundamental, especially when dealing with variables and constants in mathematical solutions. Below are some of the key ways in which integers influence algebraic work:
- Defining Variables: Integers can represent unknown quantities in an equation, making them vital for solving for unknown values.
- Significant Operations: Adding, subtracting, multiplying, and dividing integers are some of the most common operations used to simplify and solve equations.
- Equation Balancing: Integers help maintain balance in equations, ensuring that both sides of the equation remain equal after performing operations.
Moreover, negative integers introduce an additional layer of complexity, particularly when dealing with the subtraction or addition of values. Understanding how to handle both positive and negative numbers is essential for solving a wide range of problems, from simple arithmetic to more advanced calculations.
In conclusion, integers are indispensable in algebraic solutions. Their manipulation and understanding are key to solving equations accurately and efficiently.
How to Check Your Answers
Verifying the correctness of your solutions is a critical step in problem-solving. Whether you’re solving simple expressions or more complex equations, double-checking your work ensures that you haven’t made any mistakes. A careful review allows you to identify errors in calculation, logic, or steps taken. This process not only boosts accuracy but also reinforces your understanding of the concepts involved.
Here are some effective methods to check your work:
- Substitute Values Back: One of the most reliable ways to check your solution is to substitute the obtained result back into the original equation. If both sides of the equation balance, your solution is correct.
- Estimate: Before performing complex calculations, estimate the result. After solving the problem, compare your solution with your estimate to see if it makes sense.
- Use Alternative Methods: If possible, try solving the problem in a different way or use another method to cross-check the result. This can provide an additional layer of verification.
- Check for Consistency: Ensure that all steps and operations follow a logical sequence. A solution that jumps from one step to another without proper justification may contain errors.
By regularly applying these techniques, you can minimize mistakes and ensure that your solutions are correct. This attention to detail not only helps in exams but also enhances your overall problem-solving skills.
Explaining the Order of Operations
Understanding the proper sequence of steps when solving mathematical expressions is essential to getting the correct result. The order in which operations are performed can drastically change the outcome of a problem, making it crucial to follow a set structure. This sequence helps ensure that calculations are consistent and accurate, no matter the complexity of the problem.
The standard order of operations is typically remembered by the acronym PEMDAS, which stands for:
- Parentheses: Always begin by solving expressions inside parentheses or brackets.
- Exponents: After parentheses, simplify exponents (powers and roots).
- Multiplication and Division: Perform multiplication and division from left to right.
- Addition and Subtraction: Finally, perform addition and subtraction from left to right.
By following this order, you can ensure that you are consistently arriving at the correct solution. Skipping a step or performing operations in the wrong sequence can lead to errors that will affect the final result. Additionally, understanding this order is not only helpful for solving equations but also for simplifying complex expressions in real-world applications.
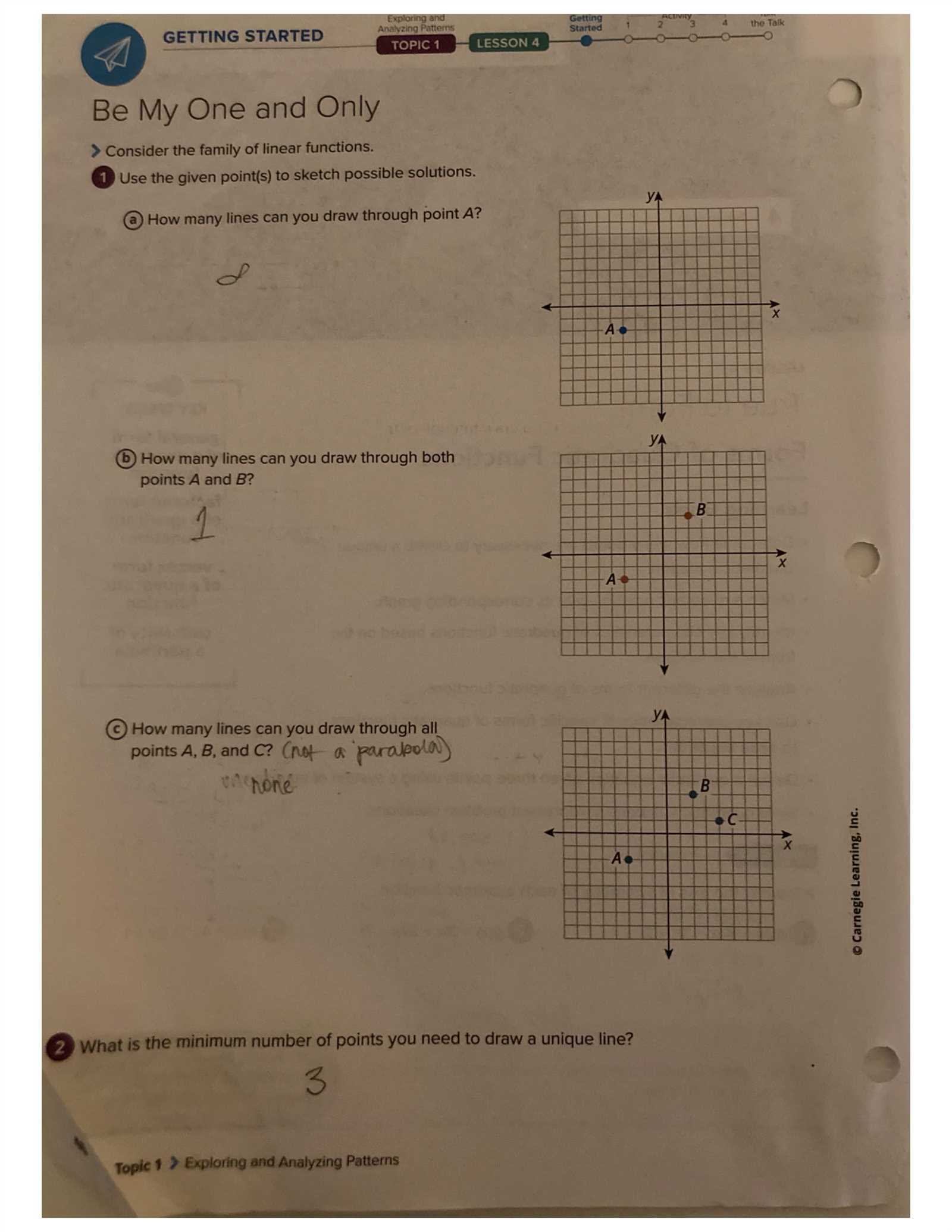
Graphing Solutions from Module 1
Graphing is an essential skill that helps to visualize the relationships between variables and provides a clear representation of equations. When solving for unknowns, plotting solutions on a graph not only verifies the correctness of the results but also gives a geometric understanding of the problem. Whether working with straight lines, curves, or systems of equations, graphing is a powerful tool for analysis.
Here are the basic steps for graphing solutions:
- Identify the equation: Start by identifying the equation or expression you need to graph. This could be a linear equation, quadratic function, or any other type of relationship.
- Find key points: Solve the equation for several values of the variable(s) to determine key points. For linear equations, finding the x and y intercepts is often helpful.
- Plot the points: Once you have the key points, plot them on a graph. Make sure to label the axes appropriately and scale the grid to suit the values you are working with.
- Draw the graph: Connect the points smoothly. For linear equations, draw a straight line; for more complex equations, draw a curve or shape that matches the function.
- Check your work: Verify that the points you plotted satisfy the original equation. If they do, your graph is correct.
Graphing solutions is a valuable skill for both theoretical learning and practical applications. By representing data visually, you can identify patterns, trends, and solutions that may not be immediately obvious from the equations alone.
Real-World Examples Using Algebra
The concepts learned in mathematical problem-solving extend far beyond the classroom. Understanding how to manipulate variables and solve for unknowns is essential in many fields and everyday situations. These skills can be applied to real-world problems in areas such as finance, engineering, science, and even everyday decision-making.
Here are some practical examples of how mathematical techniques are used in real-life situations:
- Budgeting and Finance: Suppose you want to save a certain amount of money each month to reach a goal, like purchasing a car. You can set up an equation to figure out how much you need to save each month based on your desired amount and timeframe. This involves solving for the unknown amount in the equation.
- Cooking and Recipe Scaling: If a recipe is designed for 4 servings but you need to prepare food for 10, you can use basic problem-solving techniques to scale the ingredients accordingly. By setting up a ratio or proportion, you can calculate the required quantities to adjust the recipe.
- Travel and Distance: When calculating travel time or distance, you might use equations involving speed, time, and distance. For instance, if you know the speed of your car and the time you’ll be driving, you can calculate the distance traveled by solving for the unknown.
- Construction and Design: In construction, whether it’s building a fence or designing a piece of furniture, knowing how to solve for dimensions and measurements is crucial. You may need to calculate the total area, determine the material quantities, or solve for angles in construction plans.
- Shopping Discounts: Calculating discounts or sales prices is another real-world application. If an item is discounted by a certain percentage, you can calculate the sale price by setting up an equation to solve for the final price after the discount is applied.
By applying these techniques in everyday scenarios, individuals can make informed decisions, optimize resources, and solve problems effectively. The use of equations and variable manipulation becomes an invaluable tool in a wide range of professional and personal tasks.
Preparing for Assessments
Effective preparation for assessments is essential to demonstrate your understanding and mastery of key concepts. By focusing on the core topics and practicing the application of various techniques, you can approach your evaluation with confidence. A structured approach to studying will help ensure that you are well-prepared and ready to solve problems efficiently under time constraints.
Review Key Concepts and Techniques
Start by revisiting the foundational concepts covered in your lessons. Focus on understanding the underlying principles that guide problem-solving methods, such as simplifying expressions, solving for variables, and using formulas. It’s important to know not only how to apply these techniques but also why they work in different contexts. Reviewing key strategies will make the application of concepts smoother when faced with different types of problems.
Practice Regularly with Sample Problems
One of the best ways to prepare is through consistent practice. Working through sample problems similar to those you expect on the assessment will improve your problem-solving skills. Begin with simple exercises and gradually move to more complex scenarios. Use practice questions from textbooks, online resources, or class materials to familiarize yourself with various problem types. The more you practice, the quicker you’ll be able to identify patterns and choose the best approach for each problem.
Additionally, consider practicing under timed conditions to simulate the actual test environment. This will help you build confidence, manage time effectively, and reduce anxiety during the assessment. By breaking down each problem and carefully following steps to reach a solution, you’ll be able to demonstrate a clear understanding of the material.