Geometry 10.4 Answers Explained

In this section, we explore essential principles that form the foundation of various geometric problems. The focus is on providing clear solutions and insights into common mathematical challenges, helping learners improve their problem-solving skills.

Problem-solving techniques are emphasized to guide you through complex exercises. Whether it’s triangular relationships, the application of different formulas, or recognizing patterns, this guide will make it easier to grasp the core concepts.

The aim is to simplify complex ideas and break down steps so that even the most intricate problems become manageable. By understanding the reasoning behind each solution, students can gain confidence and improve their performance.

Geometry 10.4 Answers

This section provides a comprehensive guide to solving common problems in geometric theory. By working through the steps and understanding the reasoning behind each solution, learners can gain a deeper understanding of how to approach and solve geometric challenges with confidence.

Understanding Key Techniques

To effectively solve problems in this area, it is essential to be familiar with certain methods and approaches:

• Applying logical reasoning to deduce unknown values
• Recognizing and using key theorems for solving complex problems
• Breaking down complicated shapes into simpler, manageable parts
• Practicing with various types of problems to build familiarity

Common Mistakes and How to Avoid Them

While working through problems, it’s easy to make certain errors. Here are some of the most frequent mistakes and how to avoid them:

• Misinterpreting angles or side lengths in diagrams
• Forgetting to apply all conditions stated in the problem
• Failing to double-check calculations, especially with formula application
• Skipping steps that might seem trivial but are essential for accuracy

By focusing on these techniques and avoiding common pitfalls, students can significantly improve their ability to solve mathematical challenges in this field.

Key Concepts in Geometry 10.4

This section delves into the fundamental principles that underpin various mathematical problems involving shapes, angles, and spatial relationships. Understanding these core concepts is essential for effectively solving problems and gaining a deeper appreciation of the subject.

Triangular properties play a crucial role in this section. Recognizing how different angles and sides interact within different types of triangles helps simplify complex problems. Additionally, theorems related to angle sums, congruency, and similarity form the foundation for solving real-world challenges.

Another important concept is the ability to break down complex shapes into simpler parts. By doing so, intricate figures can be analyzed and solved step-by-step, making even the most difficult problems more accessible. Mastering these key ideas ensures a solid understanding of essential geometric relationships.

Understanding Triangle Properties in 10.4

Triangles are a fundamental shape in mathematics, and understanding their properties is crucial for solving various problems. The relationships between the angles, sides, and other elements of a triangle are key to unlocking many geometric challenges. Mastering these properties allows for a more structured approach to solving complex questions.

Some of the core properties to focus on include:

• Angle Sum Theorem: The sum of the interior angles in any triangle always equals 180°.
• Congruence and Similarity: Triangles with identical angles and proportional sides are congruent or similar, which simplifies many problems.
• Pythagorean Theorem: In a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides.

By understanding these relationships, students can easily determine unknown sides or angles, as well as recognize various types of triangles based on their properties. These principles serve as the foundation for more advanced concepts in spatial reasoning and measurement.

Exploring Geometric Theorems in 10.4

In this section, we focus on understanding the key theorems that govern relationships between various geometric elements. These principles provide a structured approach to solving problems, making it easier to analyze and determine unknown quantities in different figures. A solid grasp of these theorems is crucial for progressing in more advanced studies and applying concepts in practical situations.

Key Theorems and Their Applications

The following are some of the most important geometric theorems covered:

Theorem	Description	Application
Angle Sum Theorem	The sum of interior angles in any triangle is always 180°.	Used to find missing angles in triangles.
Pythagorean Theorem	In right triangles, the square of the hypotenuse equals the sum of the squares of the other two sides.	Helps determine unknown side lengths in right triangles.
Congruence Theorems	Criteria for triangles to be congruent based on side and angle relationships.	Used to prove that two triangles are identical in shape and size.

Using Theorems for Problem Solving

These theorems not only form the basis for solving problems but also help in proving further relationships in more complex shapes. By applying these principles correctly, students can solve for unknown elements, verify geometric properties, and approach difficult problems with confidence.

How to Solve Triangle Problems

Solving triangle problems requires a systematic approach to identify the given information and apply relevant mathematical principles. By understanding the relationships between angles, sides, and other geometric elements, you can break down complex problems into simpler, manageable steps. This process involves recognizing key patterns, applying formulas, and using theorems effectively to find unknown values.

Steps for Solving Triangle Problems

The following steps can guide you through solving most triangle-related problems:

Step	Action	Explanation
Step 1	Identify Known Values	Look for any given side lengths, angles, or other information provided in the problem.
Step 2	Choose the Appropriate Formula	Decide whether to use the Pythagorean theorem, angle sum theorem, or other relevant formulas.
Step 3	Solve for Unknowns	Use the chosen formula to calculate missing sides, angles, or other unknown elements.

Common Methods for Solving Triangular Problems

There are several techniques commonly used to solve triangular problems, depending on the given data. For example, when working with right triangles, the Pythagorean theorem is often applied to find missing sides. For non-right triangles, the law of sines or law of cosines may be necessary to solve for unknown sides or angles. Understanding how to apply these methods will greatly enhance your problem-solving skills.

Step-by-Step Guide to Geometry 10.4

When tackling problems in this area of study, it is essential to follow a methodical approach that breaks down the process into clear, manageable steps. This guide outlines an effective strategy to help you solve geometric problems by focusing on key principles, logical reasoning, and precise calculations. By following each step carefully, you can gain a deeper understanding and increase your problem-solving efficiency.

Step 1: Analyze the Given Information

The first step in solving any problem is to carefully examine the provided details. Identify all known values, including side lengths, angles, and any additional information given in the problem. Drawing a diagram or sketch can be extremely helpful in visualizing the situation, ensuring that you don’t overlook important data.

Step 2: Apply Relevant Theorems and Formulas

Once you have all the necessary information, choose the appropriate mathematical principles to apply. This could involve theorems like the angle sum rule, congruence theorems, or trigonometric relationships. Selecting the right approach is crucial to simplifying the problem and making calculations more straightforward.

By following these steps, you can solve even the most challenging geometric problems with confidence and clarity. Understanding the theory behind each calculation is key to mastering this area of study and improving your overall skills.

Common Mistakes in Geometry 10.4

When solving geometric problems, it is easy to make certain errors that can lead to incorrect results. These mistakes often stem from misinterpretation of the given information, incorrect application of formulas, or overlooking important details. Recognizing these common pitfalls and knowing how to avoid them can significantly improve accuracy and problem-solving efficiency.

Misinterpreting Angles and Sides

A frequent mistake is misinterpreting the relationships between angles and sides in a figure. For example, assuming that two angles in a triangle are complementary when they are not, or misapplying the properties of similar or congruent shapes can lead to incorrect conclusions. Always verify the given values and double-check that you are using the correct geometric relationships.

Forgetting to Apply Theorems or Conditions

Another common error is failing to apply all necessary conditions or theorems to the problem. For instance, not considering the angle sum property in triangles or overlooking key assumptions like parallel lines or right angles can cause a solution to be incomplete or inaccurate. It is essential to ensure that all applicable principles are used in the process of solving the problem.

By paying attention to these common mistakes and taking time to carefully review each step, you can avoid errors and approach problems with greater confidence. Mastering the fundamentals and staying vigilant during the solution process will lead to more accurate results and better understanding of the subject.

Techniques for Solving Geometry 10.4 Exercises

Effective problem-solving in mathematics relies on the application of structured methods and strategies. By utilizing the right techniques, you can simplify complex exercises, ensure accuracy, and improve overall efficiency. Whether working with angles, sides, or various geometric properties, mastering key strategies helps to break down challenges into manageable steps.

Visualizing the Problem

One of the most powerful techniques for solving geometric exercises is to visualize the problem. Drawing a clear diagram or sketch can reveal hidden relationships between elements and make the problem easier to understand. Labeling known values and identifying unknowns in your diagram ensures that no information is overlooked and provides a clear path for applying the appropriate formulas or theorems.

Step-by-Step Problem Solving

Breaking the problem down into smaller steps is crucial for accurate results. Start by identifying what is given and what needs to be found. Apply relevant principles such as angle relationships, congruency, or trigonometric functions to solve for unknown values. Taking your time with each step ensures that no errors are made and helps you understand the reasoning behind each calculation.

Using these techniques consistently will allow you to approach exercises with greater confidence and improve your problem-solving skills. By focusing on clarity, structure, and accuracy, you can solve even the most challenging geometric problems with ease.

Real-World Applications of Geometry 10.4

Mathematical principles, particularly those related to shapes, angles, and spatial relationships, have practical uses in various fields beyond the classroom. The concepts learned in this area are applied in real-world scenarios ranging from engineering and architecture to computer graphics and physics. Understanding these applications highlights the importance of geometry in solving everyday problems and advancing technological innovations.

Field	Application	How Geometry is Used
Architecture	Designing Buildings	Using angles, symmetry, and measurements to create stable, functional structures.
Engineering	Structural Analysis	Applying geometric principles to design safe and efficient bridges, roads, and machines.
Physics	Optics and Light Reflection	Using geometric concepts to analyze the behavior of light and shadows in various environments.
Computer Graphics	3D Modeling and Animation	Utilizing geometric shapes and transformations to create virtual environments and objects.

As shown in the table, the use of geometric principles extends far beyond theoretical exercises. Whether designing the next skyscraper, analyzing light paths, or developing interactive virtual worlds, these skills are integral to modern technology and infrastructure. Mastering these concepts opens up a wide range of career opportunities and helps improve critical thinking and problem-solving abilities.

Answer Key Explained

Understanding how to approach and solve problems in this area of study is essential for mastering the material. The answer key provides step-by-step solutions that explain the reasoning behind each step. This section breaks down the process used to reach the final solution, offering insight into the methodology and helping to clarify any doubts about the problem-solving process.

Each answer is supported by clear explanations that show how key concepts and formulas are applied in practice. By following these detailed solutions, students can see the logical flow behind the calculations and learn how to apply similar strategies to different problems. This helps not only in grasping specific topics but also in developing problem-solving skills for more advanced exercises.

Reviewing the answer key is a valuable learning tool that reinforces concepts, builds confidence, and enhances the overall understanding of the subject. It serves as a guide for students to check their work and learn from any mistakes, ensuring a deeper comprehension of the material.

Important Formulas for Geometry 10.4

In mathematics, formulas serve as essential tools for solving various types of problems. By applying the right formulas, you can calculate unknown values and make connections between different geometric properties. This section highlights key formulas used in solving problems related to shapes, angles, and measurements.

Perimeter and Area of Common Shapes

One of the first steps in solving geometric problems is to calculate the perimeter or area of different shapes. Below are some important formulas:

• Rectangle: Perimeter = 2 × (Length + Width), Area = Length × Width
• Triangle: Area = 1/2 × Base × Height
• Circle: Circumference = 2 × π × Radius, Area = π × Radius²

Pythagorean Theorem

The Pythagorean Theorem is fundamental when working with right-angled triangles. It relates the lengths of the sides of a right triangle:

• Theorem: a² + b² = c², where ‘a’ and ‘b’ are the legs of the triangle, and ‘c’ is the hypotenuse.

These formulas are just a few examples of the powerful tools available to solve problems. Understanding and applying them correctly allows for efficient problem-solving and a deeper understanding of geometric relationships.

Visualizing Problems in Geometry 10.4

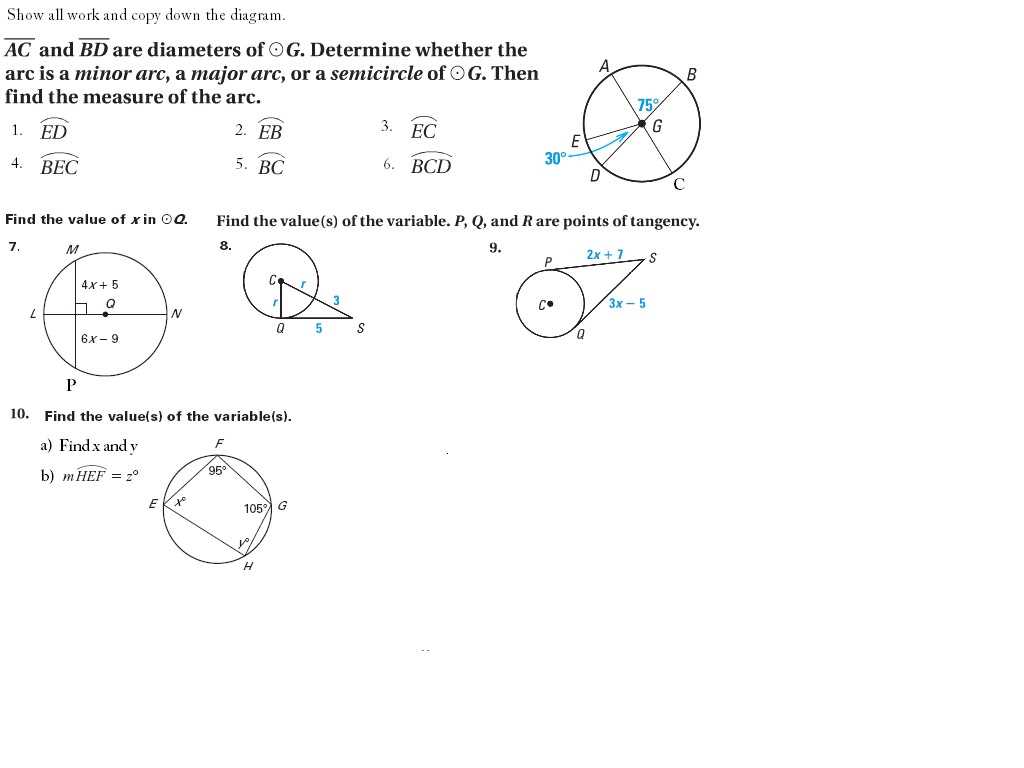
One of the most effective ways to solve mathematical problems involving shapes and measurements is by creating visual representations. By drawing diagrams or graphs, you can clarify complex relationships and make abstract concepts more tangible. Visualization helps break down difficult problems into more manageable parts and ensures a clear understanding of what needs to be solved.

When approaching geometric exercises, consider the following tips for visualizing the problem:

• Draw Accurate Diagrams: Always begin by sketching the shapes involved. Label key points, angles, and measurements to create a clear reference.
• Use Color or Symbols: Highlight different parts of the diagram to distinguish between given values, unknowns, and the relationships between them.
• Identify Key Elements: Focus on important aspects such as parallel lines, perpendicular segments, or angle relationships, and mark them clearly in the diagram.
• Break Down Complex Shapes: If the shape is complex, divide it into simpler parts (e.g., triangles or rectangles) to simplify your calculations.

By adopting these strategies, you will not only improve your understanding of geometric problems but also enhance your ability to solve them more effectively. Visualization is a powerful tool that makes abstract mathematical concepts much easier to grasp.

Tips for Mastering Geometry 10.4

To succeed in solving problems related to shapes, angles, and their properties, it’s essential to develop a solid understanding of the concepts and techniques involved. Mastering these skills requires practice, focus, and a methodical approach. By adopting a few effective strategies, you can greatly improve your problem-solving abilities and enhance your overall comprehension of the subject.

Understand Core Concepts Thoroughly

Before diving into complex problems, ensure that you have a strong grasp of the fundamental principles. This includes knowing how to calculate areas, perimeters, angles, and understanding key properties of different shapes. A deep understanding of these basics forms the foundation for solving more advanced problems.

Practice Regularly and Review Mistakes

The best way to master this subject is through consistent practice. Work on a variety of problems, from simple to more complex, to reinforce your understanding. After each exercise, take the time to review your mistakes and identify areas where you can improve. This helps solidify your knowledge and makes it easier to tackle similar problems in the future.

Additional tips:

• Draw Diagrams: Sketching out problems can clarify complex relationships and make it easier to apply formulas accurately.
• Break Down Problems: Divide large, complicated problems into smaller, more manageable steps.
• Use Online Resources: Take advantage of online tutorials, videos, and forums to get additional explanations and examples.

By following these tips, you’ll be better equipped to solve problems efficiently and develop a stronger understanding of the material. The key is persistence, practice, and continuous learning.

How Geometry 10.4 Builds on Previous Lessons

Each new concept in this field of study often builds on earlier lessons, with each stage relying on the foundational knowledge acquired in previous sections. By revisiting key principles, students can deepen their understanding and apply more advanced techniques to solve increasingly complex problems. This progression helps develop problem-solving skills and fosters a deeper comprehension of the subject as a whole.

Building on Basic Shapes and Measurements

Earlier lessons typically introduce the fundamental properties of common shapes such as triangles, circles, and polygons. As students advance, they begin applying these basic concepts to more complex scenarios, like determining unknown angles or lengths based on previously learned rules. The ability to recognize these shapes and their properties is essential when tackling more advanced topics.

Expanding on Angle Relationships

Angle relationships, such as complementary, supplementary, and vertical angles, are often explored in earlier chapters. In more advanced exercises, students use these relationships in combination with other concepts, such as parallel lines and transversals, to solve more intricate problems. Building on these concepts creates a stronger understanding of how angles function together within different geometric configurations.

By continuously linking new material to what has been previously learned, students can navigate through more advanced topics with ease. This incremental approach ensures that each new challenge becomes more manageable, reinforcing learning at every step.

Geometry 10.4 Problem-Solving Strategies

When tackling complex mathematical problems, having a clear strategy can make all the difference. Effective problem-solving often involves breaking down tasks into manageable steps, applying logical reasoning, and utilizing known formulas or properties. By adopting systematic approaches, students can approach even the most challenging exercises with confidence and clarity.

Step-by-Step Approach

One of the most effective strategies is to break down a problem into smaller, more manageable parts. This method allows you to focus on each individual aspect of the problem and solve them one at a time. Here’s how you can apply this approach:

• Understand the problem: Read through the question carefully to determine what is being asked and what information is provided.
• Organize the information: Write down the given values, properties, and any other relevant data.
• Choose the correct method: Identify which formula or theorem best fits the situation.
• Solve step-by-step: Apply the appropriate formulas and simplify the problem step by step.
• Verify the solution: Double-check your answer to ensure it aligns with the given conditions.

Visualizing the Problem

Many problems become easier to solve when you visualize them. Drawing a diagram or sketching out the situation can provide clarity and help you see relationships between different elements. Here’s how visualizing can aid problem-solving:

• Identify key components: Label important parts of the figure, such as angles, sides, or points of intersection.
• Spot patterns: Look for patterns in the diagram that may help simplify the problem.
• Apply geometric principles: Use your understanding of geometric relationships to make connections and find solutions.

By incorporating these problem-solving strategies, students can approach exercises with a clear and focused mindset, improving both their accuracy and efficiency in solving complex challenges.

Advanced Topics in Geometry 10.4

As learners progress in their studies, they encounter increasingly sophisticated concepts that build on foundational knowledge. Advanced topics challenge students to think critically and apply previously learned principles in more complex scenarios. These topics often involve deeper exploration of mathematical relationships, offering opportunities to expand problem-solving skills and enhance understanding of spatial reasoning.

Exploring Advanced Theorems

In more advanced stages of learning, students are introduced to a range of theorems that further explain the relationships between geometric objects. These theorems often serve as the backbone for solving intricate problems and are critical for understanding higher-level geometry concepts. Some key areas to explore include:

• Triangle Congruence Theorems: Understanding how different triangle properties relate to each other and how to use congruence theorems to solve problems.
• Circle Theorems: Exploring the properties of circles, including tangents, secants, and arcs, and how to apply these in more complex geometric situations.
• Coordinate Geometry: Analyzing geometric figures through a coordinate plane and using algebraic methods to solve spatial problems.

Utilizing Proofs and Postulates

One of the most powerful tools in advanced geometry is the ability to create proofs and apply postulates. Proofs not only help validate concepts but also strengthen logical reasoning. Some important strategies include:

• Direct Proof: Using known facts to directly prove the given statement step by step.
• Inductive Reasoning: Using patterns and observations to generalize and form conjectures about geometric relationships.
• Proof by Contradiction: Assuming the opposite of the statement and showing that it leads to a logical contradiction, thereby proving the original statement true.

By diving into these advanced topics, students gain a deeper and more robust understanding of mathematical structures, allowing them to tackle even the most complex geometric challenges with confidence and skill.