Secondary One Mathematics Integrated Approach Module 5 Answers

In this section, we will explore fundamental ideas and problem-solving techniques that are essential for building a solid foundation in mathematics. Whether you are looking to improve your skills or gain a deeper understanding of the subject, this guide provides valuable insights and practical solutions to common challenges faced by learners. With a clear focus on strengthening critical thinking and analytical abilities, this resource is designed to help you master the key concepts effectively.

Throughout this guide, you will find carefully explained steps for solving problems, strategies for tackling complex scenarios, and tips to avoid common mistakes. Each concept is presented in a way that is easy to follow, ensuring that learners at all levels can benefit from the information. By developing a strong grasp of these principles, you will be better prepared for future studies and assessments.

Understanding Key Solutions in Mathematics

In this section, we will explore how to effectively tackle mathematical challenges through clear steps and logical reasoning. The focus is on breaking down complex problems into manageable parts, providing clarity and direction for students seeking to improve their problem-solving skills. By emphasizing strategic thinking, this guide aims to empower learners with the tools necessary to handle various types of questions with confidence.

Breaking Down Common Challenges

One of the main obstacles faced by learners is how to approach problems that seem overwhelming at first glance. This section provides techniques to simplify calculations and enhance understanding, ensuring that each concept is grasped thoroughly before moving on to more complex ideas. By following the outlined steps, learners can gradually build their proficiency, overcoming difficulties with each practice session.

Mastering Essential Techniques for Success

Each solution in this guide is designed to strengthen essential skills such as critical thinking, pattern recognition, and logical deduction. These techniques not only help with individual problems but also lay the groundwork for future studies. As you progress, the ability to apply these methods will become second nature, paving the way for continued success in the subject.

Overview of Module 5 in Mathematics

This section focuses on the key concepts and techniques covered in the fifth segment of the curriculum. It aims to provide students with a deeper understanding of the essential skills required to solve problems effectively. The module introduces new ideas while reinforcing previously learned material, ensuring a comprehensive grasp of the subject matter.

Key Topics Covered

• Understanding fundamental principles of equations
• Exploring geometric shapes and their properties
• Learning strategies for problem-solving in various contexts
• Connecting different areas of study for a holistic understanding

Skills Developed in This Section

1. Critical thinking and logical reasoning
2. Analytical skills for approaching complex problems
3. Application of mathematical concepts in real-life scenarios
4. Improved accuracy and efficiency in calculations

This segment serves as a bridge between basic concepts and more advanced topics, ensuring that students are well-prepared for future challenges in the subject. By mastering these skills, learners will gain confidence in their abilities to tackle increasingly difficult tasks.

Key Concepts in Integrated Approach

This section explores the core ideas that form the foundation of this study area. It focuses on connecting various mathematical principles, ensuring that students can see the relationships between different topics. The goal is to foster a deeper understanding by demonstrating how these concepts work together in problem-solving scenarios.

Understanding Fundamental Principles

At the heart of this approach is the understanding that mathematical concepts are interconnected. Rather than viewing each topic in isolation, students learn to apply multiple techniques simultaneously, creating a more comprehensive method for solving complex problems. This interconnectedness encourages learners to think critically about the concepts and recognize patterns across various mathematical areas.

Strategies for Effective Problem Solving

Another key concept is developing effective strategies for tackling problems. These strategies involve breaking down problems into simpler parts, analyzing each element carefully, and applying the right techniques in a logical sequence. By mastering these methods, students can approach even the most difficult challenges with confidence and clarity.

Understanding Problem-Solving Techniques

Effective problem-solving is a crucial skill in any area of study. It involves analyzing a situation, breaking it down into smaller, manageable parts, and applying the right methods to reach a solution. In this section, we will explore various techniques that help students approach challenges with clarity and confidence, improving their ability to tackle problems from different perspectives.

The first key step in solving problems is identifying the type of challenge at hand. This allows learners to select the most suitable method for solving it. By practicing different techniques, students can learn to approach problems logically, organize their thoughts, and avoid common pitfalls. Additionally, developing a strategic mindset enables students to solve more complex problems efficiently.

Step-by-Step Solutions for Each Question

Breaking down each problem into clear, manageable steps is key to mastering any subject. This section provides detailed guidance on how to approach individual challenges, ensuring that each step is fully understood before moving on to the next. By following these systematic solutions, learners can build confidence and gradually improve their problem-solving abilities.

Guided Problem Breakdown

Each question is carefully analyzed and solved in a structured manner, highlighting the critical steps required to reach the correct answer. Here are the key phases in solving any problem:

• Identify the problem and determine the relevant information.
• Break the problem down into smaller components.
• Apply the appropriate method or formula.
• Perform the necessary calculations and double-check the results.
• Reevaluate the answer to ensure it makes sense in the context.

Practice with Detailed Explanations

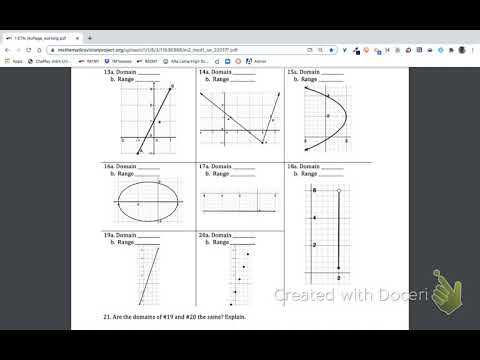
By following each solution step-by-step, learners can gain a deeper understanding of the process. The more practice they get with these types of problems, the more intuitive the steps will become. These detailed explanations offer the perfect opportunity to solidify fundamental skills, ensuring that students are ready for more complex tasks ahead.

Mathematical Strategies for Module 5

In this section, we explore key strategies designed to enhance problem-solving skills and improve efficiency in tackling various types of questions. By applying these methods, students can develop a systematic approach to mathematical challenges, ensuring they are well-prepared to handle increasingly complex topics. Each strategy is built around logical reasoning and careful analysis to maximize understanding and accuracy.

Effective Methods for Problem Solving

There are several strategies that can help students approach problems with greater confidence. These methods are particularly useful for organizing thoughts and applying the right tools to each problem:

Strategy	Description
Break it Down	Divide complex problems into smaller, more manageable steps to simplify the solution process.
Look for Patterns	Identify trends or repetitions within the problem to make predictions and simplify calculations.
Work Backwards	Start with the solution and reverse-engineer the steps needed to reach it, especially for word problems.
Use Visualization	Draw diagrams or create models to better understand the relationships between different elements.

Applying Strategies to Different Types of Questions

By using these strategies, students can approach different types of questions with a clearer and more methodical mindset. Whether it’s algebra, geometry, or word problems, these techniques ensure that every problem is tackled with the right mindset and tools for success. The key is consistency–regularly applying these strategies will help solidify their effectiveness in every learning scenario.

Common Mistakes to Avoid in Calculations

When working through mathematical problems, it’s easy to make small errors that can lead to incorrect results. Being aware of common mistakes can help students identify where they might go wrong and correct these issues early on. By understanding the most frequent missteps, learners can improve their accuracy and develop a more systematic approach to solving problems.

Typical Errors in Calculations

Below are some of the most common mistakes that can occur during calculations:

• Misplacing decimal points, leading to incorrect values.
• Forgetting to apply the correct order of operations (PEMDAS).
• Not simplifying expressions properly before solving.
• Skipping steps in multi-step problems, which can cause errors in final answers.
• Incorrectly interpreting the problem or misreading the given information.

How to Prevent These Mistakes

To avoid these errors, consider the following tips:

1. Double-check your work at each step to ensure accuracy.
2. Always follow the correct order of operations to prevent confusion.
3. Review the problem carefully before starting and ensure you understand each element of the question.
4. Use a calculator when necessary, but be cautious of input errors.
5. Take your time and avoid rushing through problems to minimize careless mistakes.

By staying mindful of these potential pitfalls and practicing these preventive strategies, students can enhance their problem-solving skills and avoid common miscalculations that might otherwise lead to frustration or incorrect answers.

Exploring the Core Mathematical Ideas

At the heart of this section are the fundamental concepts that form the foundation of problem-solving and analytical thinking. These key principles help students not only understand the structure of the subject but also gain the tools needed to tackle a wide variety of challenges. By grasping these core ideas, learners can connect different topics and apply them in real-world scenarios.

In this section, we will focus on the most important ideas that students need to master to advance their understanding. These include basic operations, the relationships between numbers, and how to apply logical reasoning to solve problems. Below is a summary of the essential concepts:

Core Concept	Description
Numbers and Operations	Understanding how numbers interact and the basic operations of addition, subtraction, multiplication, and division.
Relationships and Patterns	Recognizing connections between numbers and identifying repeating patterns to simplify problem-solving.
Problem Solving Techniques	Using logical reasoning and strategies to break down and solve complex problems step by step.
Geometrical Relationships	Understanding shapes, their properties, and how they relate to each other in space.

By thoroughly exploring and practicing these core concepts, students will be able to build a solid mathematical foundation. This understanding will not only help them solve problems more efficiently but also provide them with the skills to approach more advanced topics in the future.

Visual Aids and Diagrams for Better Clarity

Visual tools such as diagrams, charts, and graphs play a vital role in enhancing comprehension and providing a clear understanding of complex concepts. By presenting information visually, learners can better grasp relationships between variables, identify patterns, and visualize solutions in a way that words alone might not convey. These aids help simplify complicated ideas and make them more accessible.

In this section, we explore how visual aids can be used effectively to clarify various concepts. Whether it’s through geometric diagrams, number lines, or flowcharts, these tools provide immediate insight into problems, making it easier for students to focus on key elements without getting overwhelmed by abstract details.

Common Types of Visual Aids

The following visual aids are commonly used to help break down mathematical concepts:

• Graphs: These help represent data points and relationships between variables, making it easier to spot trends and patterns.
• Diagrams: Geometric diagrams, such as shapes and angles, provide a visual representation of spatial relationships.
• Flowcharts: These show step-by-step processes or decision-making paths, offering a structured way to approach problems.
• Tables: Organizing information in a table format allows for easier comparison and identification of key values.
• Number Lines: Useful for visualizing the position of numbers in relation to one another, especially for concepts like addition, subtraction, and fractions.

How to Use Visual Aids Effectively

To get the most out of visual aids, it’s important to:

1. Ensure that the visuals are clearly labeled and easy to interpret.
2. Use them alongside written explanations to reinforce understanding.
3. Focus on the most relevant information and avoid cluttering the diagram with unnecessary details.
4. Practice interpreting visuals regularly to build confidence in using them as a problem-solving tool.

By incorporating visual aids into the learning process, students can improve their ability to visualize problems and understand abstract concepts more clearly, ultimately leading to a stronger grasp of the material. These tools provide a powerful method for reinforcing knowledge and promoting deeper understanding.

How to Approach Word Problems Effectively

Word problems are often considered one of the most challenging aspects of solving mathematical tasks, but they can be tackled systematically with the right approach. By breaking down the problem step by step and focusing on key information, students can make these types of questions much more manageable. The key to solving word problems is understanding what is being asked and identifying the best strategy to find the solution.

In this section, we will explore an effective method for solving word problems. It involves careful reading, identifying important details, translating words into mathematical expressions, and finally applying the appropriate operations to reach a solution.

Steps to Solve Word Problems

To solve word problems efficiently, follow these steps:

1. Read the Problem Carefully: Ensure that you fully understand the question before starting. Pay attention to any keywords or numbers that are important for solving the problem.
2. Identify the Key Information: Highlight or underline important details, such as quantities, relationships, and conditions. This will help you focus on the most relevant parts of the problem.
3. Translate Words into Mathematical Expressions: Convert the information from the problem into mathematical language. This could involve setting up equations, drawing diagrams, or identifying unknowns.
4. Choose the Right Operation: Determine which mathematical operations (addition, subtraction, multiplication, division, etc.) are needed to solve the problem.
5. Solve the Problem: Apply the chosen operations and solve for the unknown value or answer.
6. Check Your Solution: After solving, review your answer to ensure it makes sense in the context of the problem. Double-check calculations and ensure that your solution addresses the original question.

By following this step-by-step process, students can approach word problems with confidence and clarity. Practice will help refine these skills, making it easier to identify key elements and solve more complex problems in the future.

Critical Thinking and Analytical Skills in Math

Critical thinking and analytical skills are essential tools in solving complex problems, especially when dealing with mathematical concepts. These skills allow individuals to approach problems systematically, evaluate different strategies, and arrive at logical solutions. In the context of problem-solving, being able to think critically enables students to identify underlying patterns, make connections between ideas, and break down a problem into smaller, manageable parts.

Developing these skills not only enhances the ability to solve mathematical problems but also helps in real-life situations that require logical decision-making and effective analysis. Whether working with numbers, shapes, or equations, critical thinking helps students understand the rationale behind each step of a solution and develop a deeper understanding of the subject.

Why Critical Thinking Matters in Math

Critical thinking plays a vital role in mathematics for several reasons:

• Problem Breakdown: It helps break down complex problems into simpler components, making them easier to solve.
• Solution Evaluation: It allows for the evaluation of different solution strategies and the selection of the most efficient one.
• Pattern Recognition: Analytical thinking helps identify patterns and relationships that may not be immediately obvious.
• Logical Reasoning: It strengthens logical reasoning, ensuring that each step in the problem-solving process is based on sound principles.

Building Analytical Skills

Analytical skills can be developed through consistent practice and applying specific strategies. Below is a table outlining some methods for improving these skills:

Strategy	Benefit
Practice Problem Solving	Helps reinforce logical thinking and familiarizes students with different problem-solving techniques.
Analyze Mistakes	Identifying errors and understanding why they occurred leads to better decision-making in future problems.
Break Problems Into Steps	This approach helps reduce complexity, making problems easier to understand and solve.
Explore Multiple Solutions	Evaluating different methods for solving a problem enhances flexibility and creativity in thinking.

By practicing critical thinking and honing analytical skills, students can improve their problem-solving abilities, making mathematical challenges more approachable and engaging. These skills are fundamental not just for academic success, but also for everyday decision-making and logical reasoning in various fields.

Importance of Practice in Mastering Math

Consistent practice is crucial for achieving proficiency in solving problems and understanding key concepts. The more students engage with various exercises, the more they solidify their understanding of the material and enhance their problem-solving abilities. Math is a skill that improves with repetition, as each practice session reinforces knowledge and helps identify areas that need improvement. Through continuous practice, students build confidence and gain a deeper understanding of the subject, making challenging problems more manageable.

Practice allows learners to develop strategies, refine their techniques, and discover different methods for tackling problems. It also helps familiarize them with common patterns and shortcuts that can save time during assessments. The more frequently students apply their knowledge, the easier it becomes to recall essential formulas and concepts, leading to faster and more accurate problem-solving.

Why Practice Matters

There are several reasons why regular practice is essential for mastering skills:

• Builds Familiarity: Repeated practice makes complex ideas more familiar and accessible.
• Improves Accuracy: Regular exposure to problems helps reduce mistakes and enhances precision.
• Boosts Confidence: As students successfully solve problems, their self-assurance in handling more difficult tasks grows.
• Strengthens Retention: The more a student practices, the more likely they are to retain the information over the long term.
• Reinforces Key Concepts: Practicing a variety of problems ensures that students grasp fundamental concepts and apply them effectively.

How to Practice Effectively

While practice is essential, the quality of practice matters as much as the quantity. Here are some tips for effective practice:

• Start with Basics: Begin with simple exercises to ensure a solid foundation before moving on to more advanced topics.
• Focus on Weak Areas: Identify areas of difficulty and dedicate extra time to improving those skills.
• Mix Problem Types: Solve a variety of problems to expose yourself to different methods and approaches.
• Time Yourself: Simulate exam conditions by setting a time limit for solving problems, which helps improve speed and efficiency.
• Review Mistakes: Always go over incorrect answers to understand where mistakes were made and how to correct them.

By incorporating regular and mindful practice into their study routine, students can develop mastery in their problem-solving skills, setting a strong foundation for future academic success. With consistent effort, even the most challenging concepts become easier to understand and apply.

Solutions for Challenging Mathematical Problems

Solving complex problems requires both strategic thinking and a solid understanding of fundamental principles. These problems often push students to think outside the box and apply different methods to reach a solution. The process can be time-consuming, but with the right techniques, it becomes manageable. In this section, we will explore effective strategies for approaching and solving more difficult tasks in mathematics, which can help students tackle challenges with confidence.

Challenging problems often require a blend of various strategies such as breaking down the problem into smaller parts, identifying patterns, or using trial and error. While solving difficult problems, it is important to approach each step methodically, ensuring that every aspect of the problem is thoroughly understood. Below are some useful techniques that can help in solving more demanding questions.

Techniques for Tackling Difficult Problems

Here are a few proven methods that can make solving tough problems easier:

• Break Down the Problem: Divide the complex problem into smaller, more manageable sections. This makes it easier to identify key steps and organize the solution logically.
• Look for Patterns: Sometimes, recognizing recurring patterns or sequences within the problem can provide insight into how to solve it efficiently.
• Work Backwards: For certain problems, starting from the desired result and working backwards can help identify the steps required to reach the solution.
• Trial and Error: Experimenting with different approaches, especially when stuck, can often lead to discovering a new way to solve the problem.
• Check for Hidden Information: Make sure to carefully read through the problem and check if there is any hidden information that might help simplify the solution process.

Step-by-Step Problem Solving Example

Below is an example of how to approach a complex problem by breaking it down into smaller steps:

Step	Action	Explanation
1	Understand the Problem	Read the question carefully and identify the key elements that need to be solved.
2	Identify Known and Unknown Values	List the values given in the problem and determine what needs to be found.
3	Choose an Appropriate Method	Decide which strategy (e.g., algebraic manipulation, graphing, etc.) to apply to solve the problem.
4	Work Through the Problem	Apply the method step by step, keeping track of each operation performed.
5	Review the Solution	Double-check the solution to ensure that the steps followed were correct and the answer makes sense.

By using these strategies and practicing regularly, students can become more adept at solving even the most challenging problems. The key lies in approaching each problem with patience, persistence, and a willingness to explore multiple solutions until the correct one is found. Through consistent practice, difficult problems will become easier to navigate, and students will develop a deeper understanding of the subject.

Additional Resources for Mathematics Success

Achieving success in complex problem-solving requires not only practice but also the right tools and resources. By utilizing a variety of learning aids, students can deepen their understanding of key concepts and improve their ability to tackle difficult questions. In this section, we will explore a selection of helpful resources that can supplement learning and provide valuable insights into solving challenging tasks.

These resources include textbooks, online platforms, educational videos, and interactive tools that allow students to enhance their knowledge and sharpen their skills. By combining these materials with consistent practice, students can build a strong foundation that will serve them well in future academic challenges.

Online Platforms for Practice

There are several websites and applications designed to help students practice and master various mathematical concepts. Some notable platforms include:

• Khan Academy: A free educational platform offering lessons and exercises on a wide range of topics, from basic arithmetic to advanced problem-solving techniques.
• Wolfram Alpha: A powerful computational tool that helps students solve complex problems and provides step-by-step solutions for better understanding.
• Brilliant.org: This site focuses on interactive problem-solving, offering courses and challenges that stimulate critical thinking and analytical skills.

Interactive Tools for Visualization

Visualization plays a key role in understanding abstract concepts. Here are a few tools that can help students see mathematical principles in action:

• GeoGebra: A dynamic mathematics software that allows students to create constructions and models for geometry, algebra, calculus, and more.
• Desmos Graphing Calculator: An online graphing tool that lets students visualize equations and explore their properties in a user-friendly interface.

Using these resources regularly can significantly enhance comprehension and build confidence in solving both simple and complex problems. By supplementing traditional study with these interactive and engaging tools, students will gain a deeper, more practical understanding of the material and strengthen their problem-solving abilities.

How Module 5 Relates to Future Topics

Building a strong foundation in mathematical concepts is crucial for mastering more advanced topics. The principles explored in this section are not only important on their own but also serve as stepping stones for more complex subjects. Understanding the relationships between different areas of study will allow students to approach future challenges with confidence and clarity. This section will examine how the current material connects with what students will encounter in upcoming lessons and topics.

The knowledge gained here plays a key role in various aspects of mathematics that students will explore later. By recognizing patterns and establishing a deep understanding of the foundational skills, students will find it easier to apply these concepts in new and more challenging contexts. Moreover, this section prepares learners to tackle problems involving higher-level reasoning and critical thinking in subsequent units.

Connection to Algebraic Concepts

Many of the techniques introduced here form the basis for algebraic manipulation and equation solving that will be crucial in later studies. Key topics where these principles will be applied include:

• Solving Linear Equations: The skills learned will make solving simple and complex equations easier in future lessons.
• Polynomials and Factorization: The ability to manipulate expressions and understand their structure will be vital in algebraic expansion and factorization tasks.
• Functions and Graphing: Understanding how different operations affect functions will be essential when studying graphing techniques and transformations.

Building Towards Geometry and Calculus

In addition to algebra, the concepts covered here also lay the groundwork for geometry and calculus. Future topics will rely heavily on the visualization and problem-solving skills developed in this section:

• Geometric Proofs: Logical reasoning and step-by-step analysis will be crucial when proving theorems and solving geometric problems.
• Rates of Change: Understanding fundamental concepts will make it easier to grasp concepts such as derivatives and rates of change in calculus.

By mastering the material in this section, students will build the skills necessary to handle increasingly complex mathematical topics, leading to a greater understanding of how different mathematical ideas interconnect and reinforce each other.

Time Management Tips for Completing Assignments

Effective time management is a key factor in successfully completing tasks and assignments. When students are able to organize their time well, they reduce stress and improve the quality of their work. This section will explore various strategies that can help manage time more efficiently, ensuring that deadlines are met without compromising the quality of the work.

Learning to balance study, personal time, and extracurricular activities is essential. Planning ahead and breaking down large tasks into smaller, more manageable steps can lead to a more structured and productive approach. By following these tips, students can create a clear path to success in their academic responsibilities.

Set Clear Goals and Prioritize Tasks

Before starting any assignment, it’s important to define clear goals and understand the priorities. This helps to maintain focus and ensures that essential tasks are completed first. Some helpful tips include:

• Break down larger assignments: Divide the task into smaller sections, focusing on one section at a time.
• Set realistic deadlines: Allocate specific time slots for each part of the task and stick to them.
• Identify urgent tasks: Prioritize tasks that have earlier deadlines or are more complex.

Use Tools and Techniques for Effective Scheduling

In addition to setting goals, using various scheduling tools can greatly enhance time management. Here are some methods to keep track of your progress:

• Use a planner or calendar: Write down important deadlines and review your schedule regularly.
• Time-blocking technique: Allocate fixed time periods for focused work, minimizing distractions.
• Set reminders: Use digital tools to set alerts for deadlines or upcoming tasks.

By managing time effectively and staying organized, students can stay on top of their assignments, avoid last-minute stress, and achieve better results. The key is to plan ahead, stay disciplined, and adjust the strategy as needed to accommodate changing schedules.

How to Prepare for Module 5 Assessments

Preparation for assessments is a critical part of the learning process. It requires both time management and strategic study techniques to ensure you are ready for the upcoming evaluation. This section will discuss practical steps to effectively prepare, allowing you to maximize your performance during assessments.

The key to successful preparation is understanding the scope of the material covered and focusing on areas that may require extra attention. By reviewing core concepts, practicing problem-solving techniques, and staying organized, you can approach your assessment with confidence and clarity.

Review Core Concepts and Key Skills

Before diving into practice questions, it is important to review the fundamental concepts and skills. Focus on understanding the key ideas, rather than memorizing information. Some tips to guide your review:

• Identify key topics: Highlight the most important concepts that are likely to appear on the assessment.
• Clarify doubts: If you encounter challenging concepts, seek help from teachers, tutors, or classmates.
• Summarize notes: Create concise summaries or mind maps to visualize important ideas.

Practice Regularly and Test Yourself

Consistent practice is essential to reinforce your understanding. The more you practice, the more confident you will feel in applying concepts during the assessment. Here’s how you can make the most of your practice time:

• Work through example problems: Solve a variety of problems to strengthen your problem-solving skills.
• Simulate exam conditions: Practice under timed conditions to get accustomed to the pace of the test.
• Review mistakes: After practicing, go over any errors you made to understand where you went wrong.

By reviewing the content thoroughly, practicing consistently, and focusing on improving areas of weakness, you will be well-prepared to perform at your best during the assessment. Effective preparation will not only enhance your knowledge but also build confidence in applying what you’ve learned.