Algebra 2 Test 2 Answers and Solutions Guide

In this section, we focus on breaking down the crucial elements that will help you grasp the core principles of advanced mathematical problems. Whether you’re reviewing for an upcoming assessment or aiming to deepen your understanding, it’s essential to approach each topic methodically and with clear strategies.

Mastering the techniques requires not just memorization but an understanding of how various concepts interconnect. By studying examples and practicing step-by-step methods, you can unlock the process behind solving complex problems.

In this guide, we will explore the different types of challenges typically encountered, offering solutions that highlight the best approaches to tackle each one. The goal is to build both confidence and expertise, making your journey through higher-level mathematics smoother and more intuitive.

Algebra 2 Test 2 Answers Overview

This section provides a comprehensive look at the solutions to common mathematical challenges found in higher-level assessments. It aims to guide you through the problem-solving process, offering a deeper understanding of how to approach and solve different types of questions effectively.

By reviewing these solutions, you will gain insight into the methods used to tackle various problem types, from equations to graphing. The goal is to demonstrate not only how to arrive at the correct solution but also to show the underlying principles that make the process work. This overview highlights key strategies for successfully navigating complex problems and reinforces important concepts that will help you build a stronger foundation for future studies.

Key Concepts Covered in Test 2

This section focuses on the core ideas and principles typically examined in more advanced problem-solving exercises. Understanding these concepts is crucial for mastering the techniques needed to solve complex problems and build a solid foundation in mathematics.

The key concepts covered in this assessment include:

• Quadratic Equations: Identifying solutions and understanding the relationships between roots and coefficients.
• Rational Expressions: Simplifying and solving problems involving fractions with polynomials.
• Systems of Equations: Solving linear and nonlinear systems using various methods such as substitution and elimination.
• Exponential and Logarithmic Functions: Understanding their properties and applying them in various contexts.
• Polynomial Functions: Analyzing the behavior of higher-degree functions and their graphs.

These topics form the backbone of more advanced studies, and having a solid grasp of these concepts will significantly improve your problem-solving skills and prepare you for more challenging material in the future.

Common Mistakes in Algebra 2

In the study of advanced mathematical concepts, certain errors tend to recur. These mistakes often arise from misunderstandings of key principles or from rushing through calculations without proper attention to detail. Identifying and correcting these common pitfalls is essential for improving accuracy and mastering the material.

Some of the most frequent mistakes include:

• Sign errors: Failing to correctly handle positive and negative signs, especially when simplifying expressions or solving equations.
• Incorrect factoring: Not properly factoring quadratics or higher-degree polynomials, leading to wrong solutions.
• Misapplying formulas: Using the wrong formula for a given problem or incorrectly substituting values.
• Skipping steps: Rushing through problems and skipping intermediate steps, which can lead to overlooked mistakes.
• Not checking solutions: Failing to verify solutions by substituting them back into the original equation or problem.

By being aware of these common mistakes and taking extra care in your approach, you can avoid these errors and improve both your problem-solving speed and accuracy.

Step-by-Step Solutions for Algebra 2

Breaking down complex problems into manageable steps is essential for understanding the solution process and achieving success. By following a clear sequence of logical steps, you can simplify even the most challenging exercises and ensure accuracy in your results.

Here’s how to approach a typical problem, step by step:

1. Read the Problem Carefully: Understand what is being asked before starting the solution process. Identify the key elements such as variables, coefficients, and operations.
2. Set Up the Equation: Express the problem mathematically by writing out an equation or system of equations that represents the situation.
3. Simplify the Expression: Combine like terms and reduce any complex expressions to their simplest form.
4. Apply the Appropriate Method: Choose the best technique for solving, whether it’s substitution, elimination, or factoring.
5. Check Your Work: Substitute the solution back into the original equation to verify its correctness.

By following these steps consistently, you’ll build confidence in solving problems and improve your overall problem-solving skills. Each solution is an opportunity to strengthen your understanding and approach to different mathematical challenges.

Understanding Quadratic Functions

Quadratic functions play a central role in advanced mathematics, representing relationships where the highest power of the variable is squared. These functions model a wide range of real-world situations, from projectile motion to profit maximization, and understanding their properties is key to solving many types of problems.

At the core of quadratic functions is the equation in the form of ( y = ax^2 + bx + c ), where ( a ), ( b ), and ( c ) are constants. The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the sign of ( a ). Key features of the graph include the vertex, the axis of symmetry, and the x-intercepts, which are often referred to as the roots or solutions of the equation.

By mastering the techniques for analyzing and graphing quadratic functions, you will gain the ability to solve a wide variety of mathematical problems. Understanding how the values of ( a ), ( b ), and ( c ) affect the graph’s shape and position is essential for both solving equations and interpreting real-world scenarios accurately.

Solving Systems of Equations

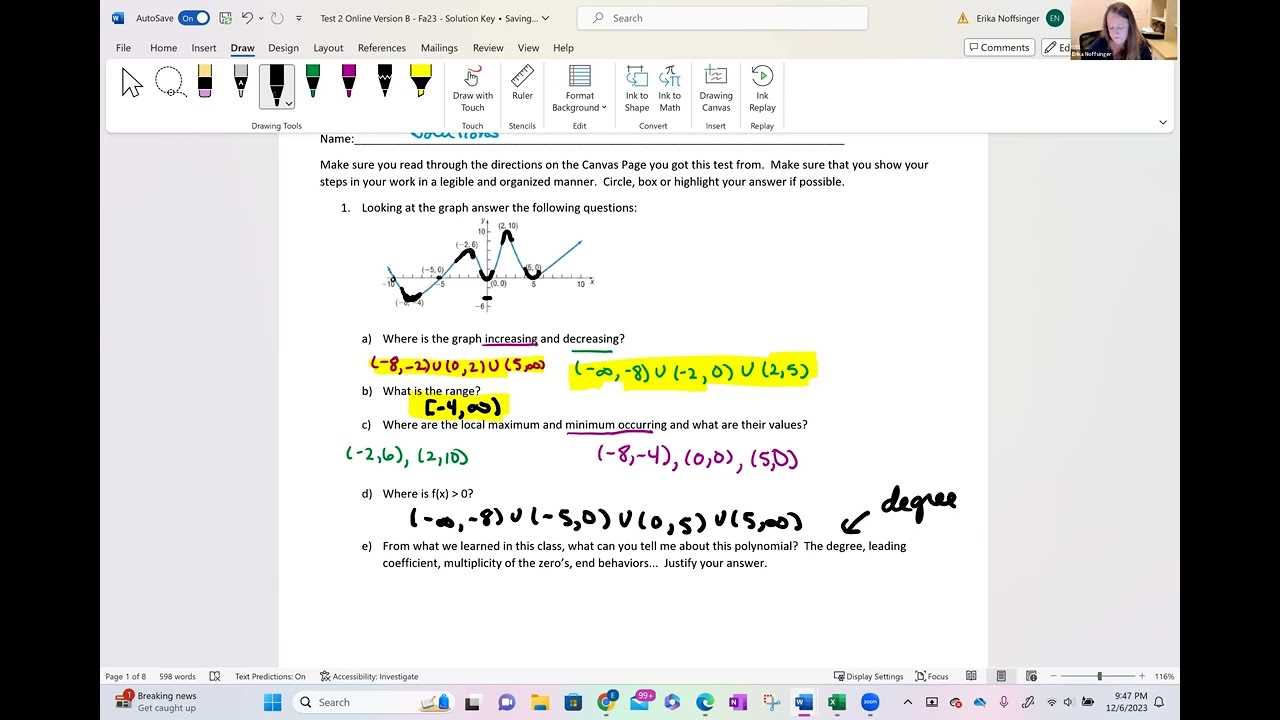
Solving systems of equations involves finding the values of variables that satisfy multiple equations simultaneously. These problems are essential in modeling situations where more than one relationship needs to be considered at the same time, such as in business, physics, and engineering scenarios. Understanding how to solve them efficiently is key to solving more complex problems in advanced mathematics.

Methods for Solving Systems

There are several methods for solving systems of equations, each suited to different types of problems. The most common methods include:

• Substitution Method: This involves solving one equation for one variable and then substituting that expression into the other equation to find the second variable.
• Elimination Method: Here, you add or subtract the equations to eliminate one variable, making it easier to solve for the remaining variable.
• Graphing Method: By graphing both equations on the same coordinate plane, the solution is the point where the two lines intersect.

Checking the Solution

After finding the solution using any of these methods, it’s important to substitute the values back into the original system of equations to verify that they satisfy both equations. This step ensures the solution is correct and that no mistakes were made during the solving process.

Working with Rational Expressions

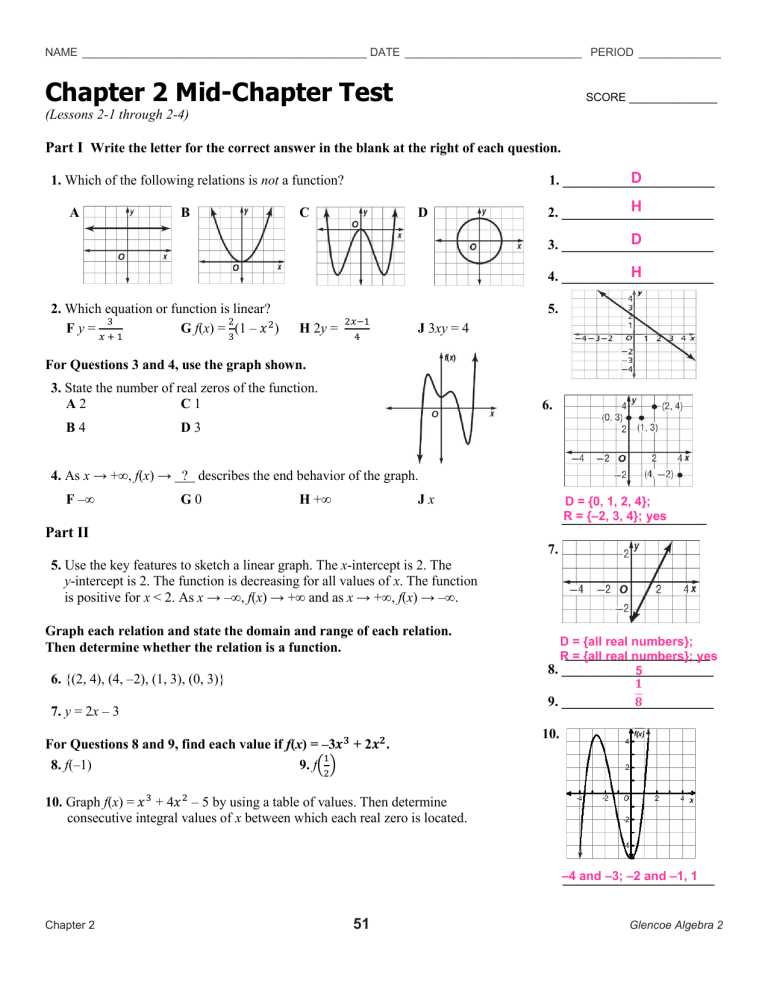
Rational expressions involve ratios of polynomials and can be found in various real-world problems, such as calculating rates, solving for unknowns in scientific contexts, and optimizing functions in engineering. Working with these expressions requires understanding how to simplify, multiply, divide, add, and subtract them while being mindful of restrictions such as denominators becoming zero.

Simplifying Rational Expressions

To simplify a rational expression, follow these steps:

1. Factor the numerator and denominator: Look for common factors that can be canceled out to simplify the expression.
2. Cancel common factors: After factoring, cancel out any factors that appear in both the numerator and denominator, reducing the expression to its simplest form.
3. Check for restrictions: Ensure that the values which make the denominator zero are excluded from the solution, as division by zero is undefined.

Operations with Rational Expressions

Performing arithmetic operations with rational expressions involves similar steps to working with fractions. Here’s a quick guide for each operation:

• Addition and Subtraction: To add or subtract, first find a common denominator. Then, combine the numerators and simplify the resulting expression.
• Multiplication: Multiply the numerators and denominators separately, then simplify by canceling common factors.
• Division: Multiply the first fraction by the reciprocal of the second, and then simplify the result.

By mastering these operations, you can handle rational expressions effectively, making them a powerful tool in solving more complex mathematical problems.

Tips for Preparing for Algebra 2

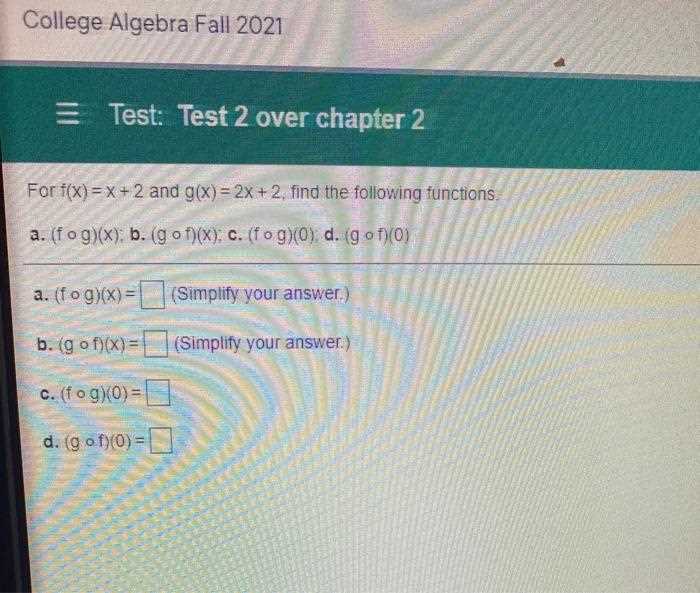
Success in advanced mathematics requires both consistent practice and a clear understanding of foundational concepts. Preparing effectively can make a significant difference in mastering complex problems and building confidence for exams. The following strategies will help you stay on track and improve your skills.

Key Strategies for Effective Preparation

• Review Core Concepts: Make sure you have a strong grasp of basic principles from previous levels. This includes operations with equations, factoring, and working with fractions.
• Practice Regularly: The more problems you solve, the more confident you’ll become. Practice a variety of problems to improve your speed and accuracy.
• Focus on Problem Areas: Identify the concepts that challenge you the most and dedicate extra time to understanding them. Don’t hesitate to ask for help if needed.
• Use Study Aids: Utilize textbooks, online resources, or study groups to reinforce what you’ve learned. Videos, tutorials, and interactive exercises can provide additional explanations.

Test-Taking Tips

• Understand the Format: Familiarize yourself with the types of questions and the format of any upcoming assessments. This will help you feel more prepared and less anxious.
• Manage Your Time: During an exam, allocate your time wisely. Start with questions that you find easier, and save more challenging ones for later.
• Double-Check Your Work: Always review your answers before submitting. Small mistakes can be easily overlooked, but taking a few extra minutes to check your work can prevent errors.

By incorporating these strategies into your preparation routine, you’ll be better equipped to handle more advanced material and perform well in your assessments.

Strategies for Time Management on Tests

Effective time management during assessments is crucial for completing all sections and ensuring the best possible results. It’s not just about how much time you spend on each question, but also about staying calm, focused, and organized throughout the exam. Proper planning and strategic thinking can help you navigate through the most challenging tasks with confidence.

Effective Time Allocation

One of the most important aspects of time management is understanding how to allocate your time appropriately. You don’t want to spend too much time on a single question while neglecting others. Here’s a general guide on how to divide your time:

Section	Time Allocation	Strategy
Easy Questions	30-40%	Start with questions you are confident about to build momentum and gain quick points.
Moderate Questions	40-50%	Allocate more time to these questions, but avoid spending too long on any single one.
Challenging Questions	10-20%	Work through these towards the end. If time runs out, leave them for review and move on.

Staying Focused and Organized

Another key element of time management is staying organized throughout the assessment. Prioritize questions, maintain focus, and keep track of the clock to avoid rushing through the final sections. Here are a few more tips:

• Read through the entire exam: Before starting, quickly skim through all the questions to understand the layout and where to focus your time.
• Mark difficult questions: If a question is challenging, don’t spend excessive time on it. Move on and come back to it later if you have time.
• Use the clock: Keep an eye on the time, and periodically check your progress to ensure you’re on track to finish everything.

By following these time management strategies, you’ll be able to approach your assessment more efficiently, reduce stress, and improve your performance overall.

Graphing Techniques for Algebra 2

Understanding how to graph equations is an essential skill in advanced mathematics. Graphing allows you to visually interpret relationships between variables and make sense of complex functions. By mastering different techniques, you can accurately plot various types of equations and gain insights that help solve problems more effectively.

There are several methods you can use to graph equations, each depending on the type of function you are working with. Whether it’s linear, quadratic, or rational functions, knowing how to approach each graphing task will help you get the right results.

Key Graphing Techniques:

• Identifying Key Points: Before plotting any function, it’s essential to find critical points such as intercepts, maxima, minima, or asymptotes. These points act as anchors for your graph.
• Using Table of Values: A helpful method for graphing is to create a table of values, where you substitute different x-values into the equation and solve for corresponding y-values. This gives you a set of points to plot on your graph.
• Intercepts and Symmetry: Recognizing where the graph crosses the x-axis (x-intercepts) or the y-axis (y-intercepts) is crucial. Additionally, certain functions have symmetry, such as parabolas, which can simplify the graphing process.
• Graphing Special Functions: For functions like parabolas or rational expressions, you should understand their unique characteristics. Parabolas have vertex points that dictate their shape, while rational functions might have asymptotes that guide your graphing technique.

Tools to Enhance Your Graphing Skills:

• Graphing Calculators: These tools can save you time and help you visualize complex equations quickly. However, it’s important to understand the underlying principles before relying too heavily on technology.
• Graphing Software: Programs like Desmos or GeoGebra allow you to input equations and immediately see the results, which is excellent for learning and verification.

By practicing these graphing techniques, you’ll develop a stronger understanding of functions and their behavior. This will not only help you in assessments but also improve your ability to solve real-world problems that involve mathematical modeling.

Using the Quadratic Formula

The quadratic formula is one of the most powerful tools in solving equations that involve squared terms. It provides a systematic method to find the solutions, or roots, of any quadratic equation, regardless of the coefficients. By using this formula, you can determine the values of x that satisfy the equation, which can then be interpreted in terms of real-world problems or mathematical models.

Quadratic Formula Explained

The quadratic formula is derived from the general form of a quadratic equation, which is written as:

ax² + bx + c = 0

To solve for x, the quadratic formula is expressed as:

x = (-b ± √(b² – 4ac)) / 2a

In this formula:

• a is the coefficient of x²,
• b is the coefficient of x,
• c is the constant term,
• ± indicates there are two possible solutions (a positive and a negative value),
• √(b² – 4ac) is called the discriminant, which tells us the nature of the roots (real or complex).

Step-by-Step Application

To apply the quadratic formula, follow these steps:

1. Identify the coefficients: From the equation ax² + bx + c = 0, determine the values of a, b, and c.
2. Calculate the discriminant: Compute the value of b² – 4ac. This will tell you whether the solutions are real or complex.
3. Substitute into the formula: Plug the values of a, b, and c into the quadratic formula.
4. Solve for x: Simplify the equation to find the two possible solutions for x.

Using the quadratic formula is an efficient way to solve for the roots of quadratic equations, especially when factoring is difficult or not possible. It is important to carefully check your discriminant to determine whether you should expect real or complex solutions.

Understanding Exponential Functions

Exponential functions are an essential class of mathematical relationships that describe processes involving growth or decay. These functions are characterized by a constant rate of change, where the variable is raised to a power. Understanding how these functions behave allows you to model real-world situations like population growth, compound interest, and radioactive decay.

Key Characteristics of Exponential Functions

Exponential functions have a distinct form, usually written as:

f(x) = a * b^x

Where:

• a is the initial value or coefficient,
• b is the base, which determines the rate of growth or decay,
• x is the exponent, which is the independent variable.

The behavior of the function depends largely on the value of b. When b > 1, the function models growth, increasing as x increases. Conversely, when 0 , the function models decay, decreasing as x increases.

Applications of Exponential Functions

Exponential functions appear frequently in various fields, particularly when modeling phenomena that change rapidly over time. Some common examples include:

• Population Growth: Many biological populations grow exponentially under ideal conditions, where the number of individuals increases at a constant percentage rate.
• Compound Interest: Financial investments often grow exponentially, with interest being added to the principal at regular intervals, leading to growth on top of growth.
• Radioactive Decay: The decay of radioactive substances follows an exponential model, with the substance decreasing at a consistent rate over time.

By understanding the fundamental characteristics of exponential functions, you can better interpret and solve real-world problems that involve rapid changes in quantities.

How to Approach Word Problems

Word problems often present real-world scenarios that require mathematical solutions. The key to solving these problems is breaking down the information provided and translating it into a format you can work with. By following a step-by-step approach, you can simplify complex situations and find the solution effectively.

Steps to Solve Word Problems

To approach word problems systematically, follow these steps:

1. Read the Problem Carefully: Make sure to read the problem multiple times to fully understand what is being asked. Pay close attention to details, such as units of measurement and specific conditions.
2. Identify the Known and Unknown: Write down the information provided and what you need to find. Label the known quantities and let variables represent unknowns.
3. Set Up an Equation: Based on the information provided, translate the words into an equation or mathematical expression. Use appropriate formulas or relationships to form this equation.
4. Solve the Equation: Perform the necessary algebraic operations to solve for the unknowns. Check your work as you go to avoid simple mistakes.
5. Interpret the Solution: Once you have found the solution, make sure it answers the question posed in the problem. Ensure the units are correct, and verify if the solution makes sense in the context of the problem.

Common Strategies for Word Problems

Here are some helpful strategies to keep in mind when solving word problems:

• Draw a Diagram: Visual aids such as graphs, charts, or drawings can help clarify the problem and guide you toward the correct solution.
• Look for Keywords: Certain words or phrases in the problem can indicate specific mathematical operations, such as “sum” for addition or “difference” for subtraction.
• Break the Problem into Parts: If the problem involves multiple steps or conditions, break it into smaller, manageable pieces. Solve each part step by step before combining the results.
• Check for Special Conditions: Sometimes, problems include special instructions, such as “round to the nearest tenth” or “find the maximum value.” Make sure to follow these instructions carefully.

By following these strategies, you can approach word problems with confidence and systematically work through them to find accurate solutions.

Analyzing Algebraic Expressions

When dealing with mathematical expressions, it is essential to understand their structure and components. By breaking down an expression into its parts, you can more easily identify the relationships between variables, constants, and operators. This process not only helps simplify the expression but also enables you to apply the correct mathematical techniques for solving or manipulating it.

To effectively analyze an expression, follow these key steps:

• Identify the Terms: Each part of an expression separated by addition or subtraction is called a term. Understanding the individual terms is crucial for simplifying or factoring the expression.
• Understand the Operations: Pay attention to the operations between terms, such as addition, subtraction, multiplication, or division. The order of operations is vital to solving the expression correctly.
• Recognize Like Terms: Like terms are terms that have the same variable raised to the same power. These can be combined through addition or subtraction, which simplifies the expression.
• Look for Exponents and Powers: Expressions often include powers or exponents. Understanding the rules of exponents allows you to simplify these parts efficiently, such as multiplying or dividing powers of the same base.

Once you have analyzed the components of the expression, you can apply various techniques, such as factoring or expanding, depending on what you need to achieve. This analysis forms the foundation for working through more complex problems and solving for unknowns.

Test 2 Frequently Asked Questions

When preparing for any assessment, it’s common to have several questions or concerns regarding the structure, content, or strategies for success. In this section, we address the most frequently asked questions to help clarify any doubts and ensure you are well-prepared for the upcoming evaluation. Whether you are curious about specific topics or the format of the assessment, this guide will offer valuable insights to ease your preparation process.

Common Concerns Before the Assessment

Many students have similar questions leading up to an evaluation, often revolving around study strategies and common challenges. Below are some of the most asked questions regarding the preparation process:

Question	Answer
What topics should I focus on?	Focus on the key concepts covered in the course, including equations, functions, and graphing. Make sure you review any challenging areas where you feel less confident.
How long should I spend studying each day?	Studying consistently over several days is more effective than cramming. Aim for 1-2 hours a day leading up to the evaluation, focusing on different areas each session.
Should I practice with past problems?	Yes! Practicing with previous problems helps you get familiar with the format and improves your problem-solving skills under timed conditions.

During the Assessment

Understanding what to expect during the actual assessment is just as important as preparing for it. Here are some common questions about the experience:

Question	Answer
How should I manage my time?	Allocate a specific amount of time to each section, leaving some extra time at the end for review. Prioritize easier questions first and tackle more challenging ones later.
Can I skip difficult questions?	Yes, if a question is taking too long, move on to the next one and return to it later. This strategy ensures you don’t waste too much time on one problem.

By understanding these frequently asked questions, you can approach your preparation and the assessment itself with greater confidence, ensuring a smoother and more successful experience.

Reviewing Algebra 2 Test 1 Answers

Reviewing previous assessments is an essential part of preparing for future evaluations. By reflecting on the problems and solutions from earlier evaluations, you can identify areas of strength as well as concepts that need further attention. This section provides an overview of key questions and detailed solutions from the first evaluation, helping you understand where you may have made mistakes and how to correct them moving forward.

Question	Solution
1. Solve for x: 3x + 5 = 20	Subtract 5 from both sides: 3x = 15. Divide both sides by 3: x = 5.
2. Simplify the expression: 2(x + 4) – 3(x – 2)	Distribute: 2x + 8 – 3x + 6. Combine like terms: -x + 14.
3. Solve for y: 4y – 6 = 18	Add 6 to both sides: 4y = 24. Divide both sides by 4: y = 6.
4. Find the value of the quadratic expression: x² + 4x + 4	This is a perfect square trinomial, which factors as (x + 2)².
5. Simplify the rational expression: (x² – 4) / (x – 2)	Factor the numerator: (x – 2)(x + 2). Cancel out the (x – 2) terms, leaving x + 2.

By working through these solutions, you can better understand how to approach similar problems in the future and avoid common pitfalls. Make sure to focus on the steps taken to arrive at the solution, as these processes are often key to solving more complex problems.

Practice Resources for Algebra 2

To strengthen your understanding and mastery of mathematical concepts, practicing regularly is essential. Utilizing various resources can significantly improve your problem-solving skills and boost your confidence. This section provides a collection of helpful materials, including online tools, worksheets, and textbooks, to guide you through the practice process.

Online platforms offer interactive exercises where you can receive immediate feedback, allowing you to track your progress. Additionally, many websites provide step-by-step tutorials to break down complex topics. These resources are ideal for reinforcing your knowledge and tackling challenging problems.

Textbooks and practice books can serve as excellent resources, offering a wide range of problems with varying levels of difficulty. These allow you to practice under timed conditions, simulating real assessment scenarios. Worksheets focused on specific topics also allow you to zero in on areas where you need more attention.

Lastly, group study sessions or tutoring can provide valuable collaborative learning opportunities. Discussing solutions with peers or instructors can often lead to a deeper understanding of difficult concepts and help you refine your approach to problem-solving.