Multiplying and Dividing Rational Expressions Worksheet Answers

In algebra, handling complex fractions involves a variety of techniques that simplify problems and make calculations more manageable. These skills are essential when solving equations that involve numerical ratios with variables. Understanding how to manipulate these forms helps students grasp more advanced concepts and apply them in real-life situations.
When it comes to solving these types of problems, learning the correct steps for combining or separating terms is crucial. Simplifying such fractions requires careful attention to detail, ensuring all parts of the problem are properly handled. By mastering these methods, learners can efficiently solve a wide range of mathematical challenges.
By practicing these strategies regularly, students can build confidence in their ability to work with complex fractions. Whether simplifying or solving equations, the goal is to develop a deeper understanding of how these forms behave and how best to manipulate them in various scenarios. Step-by-step practice helps reinforce these skills and prepares students for more advanced topics in algebra.
Multiplying and Dividing Rational Expressions Worksheet Answers
In algebra, working with fractions that include variables requires a clear understanding of the rules for combining and separating terms. This section will guide you through the essential steps to successfully solve problems involving fractional forms. Mastering these processes is key to simplifying and manipulating algebraic ratios in various equations.
Understanding Key Principles
Before diving into the problems, it’s important to review the basic principles. When working with fractional forms that include variables, always follow these key guidelines:
- Identify the numerator and denominator clearly in each term.
- Factor both the numerators and denominators when possible.
- Cancel out any common factors between the numerator and denominator.
- Apply the rules of operations carefully, ensuring that the numerator is multiplied or divided by the numerator, and the denominator by the denominator.
Step-by-Step Process
Follow these steps for solving problems that involve combining or separating terms:
- Start by factoring both the numerator and denominator of each fraction.
- Look for common factors that can be canceled out. This simplifies the equation.
- Perform the multiplication or division of the remaining terms, remembering that the operation applies to both the numerator and the denominator.
- Simplify the resulting fraction to its lowest terms, if possible.
- Double-check your final result to ensure no mistakes were made during cancellation or simplification.
By practicing these steps, students will be able to efficiently solve complex algebraic problems, gaining confidence in handling more advanced concepts. Whether simplifying a complex fraction or solving an equation, these methods are essential for success in algebra. Keep practicing with different examples to reinforce your understanding and improve your problem-solving skills.
Understanding Rational Expressions Basics
Algebraic fractions involve two key components: a numerator and a denominator, each containing one or more variables. The ability to simplify and manipulate these types of fractions is crucial for solving equations that include such forms. Understanding the core principles behind these fractions helps build a foundation for more complex algebraic operations.
Components of Algebraic Fractions
Every algebraic fraction consists of two parts: the numerator, which is the term above the fraction bar, and the denominator, which is the term below the bar. Both parts may contain constants, variables, or even other fractions. By understanding how to factor and simplify each part, the entire fraction becomes easier to work with.
- The numerator represents the “top” portion of the fraction.
- The denominator represents the “bottom” portion of the fraction.
- Both parts can include variables, constants, or expressions.
Core Operations with Algebraic Fractions
To solve equations with algebraic fractions, it is essential to know how to perform the basic operations. These operations may include factoring, canceling common terms, or simplifying fractions. The rules for working with such forms are similar to those for regular fractions, but with the added complexity of variables.
- Factor both the numerator and the denominator to identify common factors.
- Cancel out any matching terms between the top and bottom.
- Simplify the result as much as possible by reducing terms.
Mastering these techniques is a fundamental step toward solving more advanced algebraic problems. A solid understanding of these basics will allow students to approach algebraic fractions with confidence and clarity.
Step-by-Step Guide to Multiplying Expressions
When working with algebraic fractions, it is essential to understand the process of combining two separate fractions into one. The goal is to create a single fraction by multiplying the numerators and denominators of the given terms. This method helps simplify the problem and make the calculations easier to handle.
Follow these steps to successfully combine terms:
- Factor both the numerator and the denominator: Before multiplying, check if any terms in the numerator or denominator can be factored. This can make the next steps easier.
- Multiply the numerators: Multiply the top parts of both fractions together. Ensure to multiply each term in the first fraction by each term in the second fraction.
- Multiply the denominators: Repeat the process for the bottom parts of the fractions. This step will give you the denominator of the resulting fraction.
- Simplify the fraction: After multiplying, always check for any common factors in the numerator and denominator that can be canceled out to simplify the result.
- Final check: Ensure that the resulting fraction is in its simplest form. If needed, factor and reduce the terms again for clarity.
By following these steps carefully, you can handle more complex problems involving algebraic fractions and arrive at the correct solution with ease.
How to Simplify Rational Expressions
Simplifying algebraic fractions is a crucial skill in solving more complex problems. The main goal is to reduce the fraction to its simplest form by factoring and canceling out common factors between the numerator and the denominator. This process makes it easier to perform operations and solve equations involving these types of fractions.
Steps for Simplification
Follow these key steps to simplify algebraic fractions:
- Factor both parts: Start by factoring both the numerator and denominator completely. Look for common factors, and if possible, break down complex terms into simpler components.
- Cancel common factors: Once both parts are factored, identify any common terms in the numerator and denominator. These can be canceled out to simplify the fraction.
- Reduce the fraction: After canceling, make sure that the resulting terms are in their simplest form, with no further factors that can be divided out.
- Double-check: Always verify your result by checking that no further reduction is possible, and ensure the final fraction is simplified to its most basic form.
Common Mistakes to Avoid
- Not factoring completely: Incomplete factoring can lead to incorrect simplifications, so ensure all terms are fully factored.
- Canceling terms incorrectly: Only cancel out terms that appear in both the numerator and denominator. Don’t cancel terms across addition or subtraction.
- Leaving fractions unsimplified: After canceling common factors, make sure the fraction is reduced as much as possible before finalizing the solution.
By following these steps, you can confidently simplify even the most complicated algebraic fractions and make solving equations much more straightforward.
Key Rules for Dividing Rational Expressions
When working with algebraic fractions, it’s essential to understand the fundamental principles of handling division between them. Dividing involves flipping the second fraction (the divisor) and changing the operation to multiplication. This rule is crucial for simplifying complex problems and solving equations involving fractional terms.
Important Rules to Follow
Before proceeding with division, be sure to follow these key rules:
| Step | Action |
|---|---|
| 1 | Flip the divisor: Invert the second fraction so that the numerator becomes the denominator, and the denominator becomes the numerator. |
| 2 | Change the operation: After flipping, change the operation from division to multiplication. |
| 3 | Factor both fractions: Factor both the numerator and denominator of both fractions before performing any operations. This step is essential to simplify the terms. |
| 4 | Cancel common factors: Look for common factors between the numerators and denominators. Cancel them out to simplify the equation. |
| 5 | Simplify: After canceling out any common terms, simplify the resulting fraction as much as possible. |
Common Pitfalls to Avoid
To avoid errors when dividing algebraic fractions, here are some common mistakes to watch out for:
- Forgetting to flip: Remember to invert the second fraction before changing the operation to multiplication.
- Canceling terms incorrectly: Only cancel out common factors between the numerator and denominator, and never cancel terms that are not common across both fractions.
- Not factoring fully: Make sure all terms are factored completely before simplifying the fraction. This ensures you don’t miss any common factors.
By mastering these rules, you’ll be able to confidently handle the division of algebraic fractions and solve more complex mathematical problems effectively.
Common Mistakes in Multiplication
When working with algebraic fractions, errors can easily occur during the process of combining terms. These mistakes often arise from misunderstandings of the rules or skipping essential steps. Recognizing and avoiding these common errors is key to successfully solving problems and simplifying expressions.
Typical Mistakes to Avoid
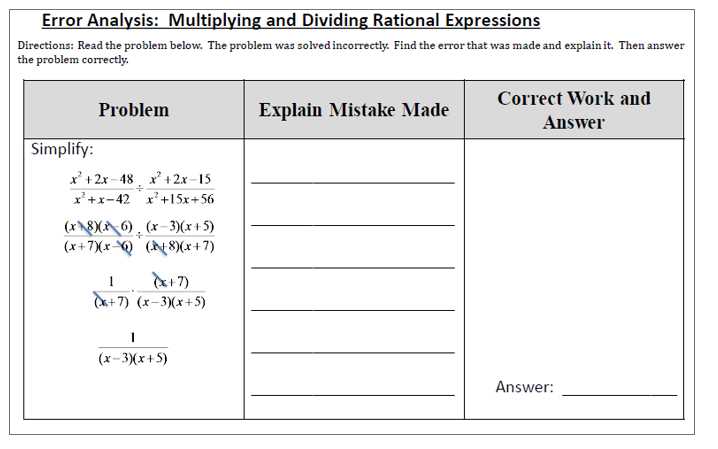
- Failing to Factor Completely: One of the most frequent errors is neglecting to fully factor the numerator and denominator before performing any operation. This leads to missed opportunities for simplification.
- Incorrectly Multiplying Across: It’s essential to multiply the terms in the numerator of one fraction with the terms in the numerator of the other, and the same for the denominators. Failing to do so can lead to incorrect results.
- Skipping Simplification: After multiplying, many forget to simplify the resulting fraction. Always look for common factors that can be canceled to make the fraction as simple as possible.
- Overlooking Negative Signs: Misplacing or neglecting negative signs during multiplication can drastically change the outcome. Always keep track of signs in both the numerator and denominator.
- Not Checking for Common Factors: Before multiplying, it’s essential to check if any common factors exist between the numerator and denominator that can be canceled out. Skipping this step leads to unnecessary complexity.
How to Prevent These Mistakes

- Factor everything: Always factor both the numerators and denominators completely before proceeding with multiplication.
- Multiply carefully: Take your time and make sure you multiply each term in the numerator with each term in the denominator, following the correct order of operations.
- Double-check your work: After multiplying, check for any common factors between the numerator and denominator, and simplify the fraction as much as possible.
- Track signs: Keep a close eye on the signs throughout the process to avoid incorrect results due to sign errors.
By being aware of these common mistakes and taking extra care in each step, you can improve your accuracy and ensure that your solutions are correct.
Techniques for Dividing Complex Fractions
Handling complicated fractions can be challenging, especially when they involve other fractions within the numerator or denominator. To simplify such problems, it’s important to understand the systematic approach required to break down and solve them effectively. By applying a series of well-established techniques, you can transform complex fractions into simpler, more manageable forms.
Step-by-Step Process
Here is an outline of the steps you can follow to handle division involving complex fractions:
- Identify the complex fraction: Look for fractions within the numerator or denominator that need to be addressed separately.
- Multiply by the reciprocal: The key to simplifying complex fractions is to rewrite the division problem as multiplication by the reciprocal of the divisor.
- Simplify the fractions: Before performing any multiplication, ensure that both the numerator and denominator of each fraction are fully simplified and factored where possible.
- Multiply the fractions: Now that you’ve changed the division to multiplication, proceed by multiplying the numerators and denominators together.
- Cancel common factors: After multiplication, check for common factors between the numerator and the denominator and cancel them out to simplify the result.
- Final simplification: Once the fractions are multiplied and common factors canceled, simplify the expression to its simplest form.
Common Strategies for Simplification
In addition to the basic steps, here are some strategies to help streamline the process:
- Factor wherever possible: Factoring both the numerators and denominators can help identify common factors that may be canceled out later.
- Use parentheses to clarify: When dealing with multiple fractions within a fraction, using parentheses can help clarify the structure of the problem and avoid mistakes during calculations.
- Check for hidden common factors: Sometimes, common factors may not be immediately obvious. Always double-check for factors that might simplify the problem further.
By following these steps and strategies, you can confidently tackle division problems involving complex fractions and arrive at a simplified, correct solution with ease.
Examples of Multiplying Rational Expressions
To gain a deeper understanding of how to handle fractions involving algebraic terms, it’s essential to explore some practical examples. By working through specific problems, we can break down the process into manageable steps, ensuring we apply the correct methods for simplifying the resulting fractions.
Example 1: Simple Fraction Multiplication
Consider the following problem:
Problem: Multiply the following fractions:
(3x / 4) * (8 / 5x)
Solution:
- First, multiply the numerators: 3x * 8 = 24x.
- Next, multiply the denominators: 4 * 5x = 20x.
- Now, the new fraction is: 24x / 20x.
- Cancel the common factor of x, simplifying the fraction to: 24 / 20.
- Finally, simplify the numbers: 24 ÷ 4 = 6 and 20 ÷ 4 = 5, so the final answer is: 6 / 5.
Example 2: Multiplying with Factoring
Consider this more complex example:
Problem: Multiply the following fractions:
(x^2 – 9) / (x^2 – 4) * (x + 3) / (x – 2)
Solution:
- Factor the quadratic terms in both the numerator and denominator where possible:
x² – 9 = (x + 3)(x – 3)
x² – 4 = (x + 2)(x – 2).
- The new expression becomes:
[(x + 3)(x – 3)] / [(x + 2)(x – 2)] * (x + 3) / (x – 2). - Now, cancel the common factors (x + 3) and (x – 2) from the numerator and denominator:
- After canceling, the remaining terms are: (x – 3) / (x + 2).
Example 3: Complex Fractions with Negative Exponents
Problem: Multiply the following fractions:
(2x⁻²) * (3x²)
Solution:
- Multiply the terms in the numerators: 2x⁻² * 3x² = 6x⁰.
- Since x⁰ = 1, the simplified result is just 6.
By following these examples, you can become proficient in working with fractions involving algebraic terms and simplify your calculations effectively. Always remember to factor where possible, cancel common terms, and simplify the resulting expressions.
Solving Real-Life Problems with Rational Expressions
Mathematical problems often arise in everyday situations, where we need to simplify fractions or combine terms involving variables. By applying the concepts learned from algebraic fractions, we can solve real-life issues in various fields, such as finance, engineering, or even cooking. Understanding how to manipulate these terms allows us to create models and make accurate predictions based on the given information.
Example 1: Budgeting for a Group Event
Imagine you are organizing a group event and need to calculate the cost per person when sharing a total amount among multiple participants. You can use algebraic fractions to model the situation effectively.
Problem: Suppose the total cost for a party with fixed charges is $600, and the cost depends on the number of people attending. If each person’s share is represented as 600 / x, where x is the number of people attending, how much will each person pay if 30 people attend?
Solution:
Substitute the number of attendees into the equation:
| Expression | Value |
|---|---|
| 600 / x | 600 / 30 = 20 |
Thus, each person would pay $20 if 30 people attend the event.
Example 2: Construction and Material Costs
In construction, you might need to determine the amount of material required for a specific project, where the quantity depends on the area to be covered.
Problem: A construction company is building a rectangular floor that is 12 meters long and 8 meters wide. If the cost to cover one square meter is $5, how much will it cost to cover the entire floor?
Solution:
First, find the area of the floor:
| Expression | Value |
|---|---|
| Area = length × width | Area = 12 × 8 = 96 square meters |
| Cost = area × cost per square meter | Cost = 96 × 5 = $480 |
The total cost to cover the floor will be $480.
These examples show how algebraic fractions can be applied to everyday scenarios. By learning to manipulate and solve these types of problems, you can make informed decisions in various practical situations.
Finding the Greatest Common Factor
When working with algebraic terms, it is often necessary to simplify or reduce fractions by finding the largest number or expression that can evenly divide both the numerator and the denominator. This is known as the greatest common factor (GCF). Identifying the GCF helps streamline expressions, making them easier to work with and solve. Whether dealing with numbers or variables, this process can significantly simplify complex problems.
Step 1: Factor Each Term
To begin finding the GCF, you must first factor each term involved. This step involves breaking down the terms into their prime factors or simplest algebraic components. For example, if you’re working with the terms 12x² and 18x, you would start by factoring these numbers:
| Term | Factoring |
|---|---|
| 12x² | 2² × 3 × x² |
| 18x | 2 × 3² × x |
Step 2: Identify Common Factors
Next, identify the factors that are common to both terms. These are the components that appear in both factorizations. In the case of 12x² and 18x, the common factors are 2, 3, and x.
Therefore, the GCF of 12x² and 18x is:
GCF = 2 × 3 × x = 6x.
By finding the greatest common factor, you can now simplify fractions or perform further algebraic operations with greater ease. This method is particularly useful when working with polynomial fractions or solving equations involving multiple terms.
Reducing Fractions in Rational Expressions
When working with algebraic terms, one of the key steps in simplifying complex formulas involves reducing fractions. This process ensures that the numbers or variables in both the numerator and denominator are expressed in their simplest form. By identifying common factors and canceling them out, you can make the fraction easier to work with and solve.
Step 1: Factor Both the Numerator and Denominator
To begin reducing a fraction, start by factoring both the numerator and the denominator into their simplest components. For example, if you’re working with the fraction 12x² / 18x, you would factor both terms:
| Term | Factoring |
|---|---|
| 12x² | 2² × 3 × x² |
| 18x | 2 × 3² × x |
Step 2: Cancel Common Factors
Once the numerator and denominator are factored, identify the common factors between them. These factors can be canceled out from both parts of the fraction. In our example, both terms share the factors 2, 3, and x, so we can cancel them:
After canceling:
The fraction becomes:
12x² / 18x = 2x
By reducing the fraction to its simplest form, the expression becomes easier to understand and work with in further calculations or problem-solving.
When to Cancel Terms in Multiplication
When working with algebraic fractions, canceling terms can simplify calculations. This step is essential in reducing the complexity of an equation, but it’s important to know when to cancel. The process should only be applied when common factors appear in both the numerator and the denominator. Canceling terms incorrectly can lead to errors and incorrect results.
Key Guidelines for Canceling
Here are the key points to remember when determining when to cancel terms:
- Both Numerator and Denominator: Only cancel terms that appear in both the numerator and the denominator.
- Factor First: Always factor the terms fully before canceling. You cannot cancel terms that are not factored into their simplest components.
- Cancel Only Common Factors: Ensure that the terms you’re canceling are factors, not parts of larger terms. For example, you can cancel 3 from both the numerator and denominator if both contain 3, but you cannot cancel 3x with 3 unless it’s factored properly.
Example of Correct Cancellation
Let’s say you have the fraction 8x / 12x². To simplify this, follow these steps:
- Factor both terms: 8x = 2³ × x and 12x² = 2² × 3 × x²
- Cancel the common factors: 2² × x are common to both terms, so cancel them.
- The simplified fraction is 2 / 3x.
By applying these guidelines, you can confidently simplify algebraic fractions and make calculations more manageable.
Identifying Undefined Expressions in Division
When working with algebraic calculations involving fractions, it’s crucial to recognize when a given problem is undefined. This typically occurs when division involves a denominator that equals zero. Since division by zero is mathematically impossible, such expressions do not yield valid results. Identifying and avoiding these cases is essential for accurate problem-solving.
Key Conditions for Undefined Terms
There are several conditions to check for when determining if an expression is undefined:
- Zero in the Denominator: If the denominator contains a value or variable that can become zero, the expression is undefined. For example, if the denominator is x – 5, setting x = 5 makes the denominator zero, thus making the expression undefined.
- Variable Restrictions: Be mindful of variable restrictions that could lead to division by zero. For example, in an expression like 1 / (x + 3), x = -3 would make the denominator zero, creating an undefined situation.
- Factoring Considerations: Before canceling terms, ensure that no variable is inadvertently being canceled with a zero denominator. Check for undefined values before simplifying the equation.
Example of Identifying Undefined Expressions
Consider the following expression:
1 / (x² – 9)
To identify if this expression is undefined, factor the denominator:
- x² – 9 = (x – 3)(x + 3)
Now, set each factor equal to zero:
- x – 3 = 0 ⟶ x = 3
- x + 3 = 0 ⟶ x = -3
Thus, the expression is undefined when x = 3 or x = -3, as these values make the denominator zero.
By following these steps, you can easily identify when an algebraic fraction becomes undefined and avoid incorrect calculations.
Multiplication of Polynomials in Rational Expressions
When working with algebraic fractions that involve polynomials, the process of combining terms can be crucial for simplifying the overall expression. In such cases, multiplying the polynomials in the numerator and denominator follows a set of rules that ensure accuracy. The key is understanding how to distribute each term properly, ensuring that no terms are missed during the multiplication process.
The general approach to handling these operations involves using the distributive property (also known as the FOIL method when dealing with binomials) to ensure that every term in the first polynomial is multiplied by every term in the second polynomial. By carefully applying this method, the resulting products can then be combined to form a simpler expression, often with fewer terms.
Steps for Multiplying Polynomials
Follow these steps to multiply polynomials effectively:
- Distribute Each Term: Begin by multiplying each term in the first polynomial with each term in the second polynomial. This ensures that no term is left out.
- Combine Like Terms: After performing the multiplications, combine any like terms that appear in the resulting polynomial. This helps to simplify the expression further.
- Check for Factoring Opportunities: In some cases, after the multiplication is complete, you may notice that factoring can simplify the expression even more.
Example of Polynomial Multiplication
Let’s consider the following two polynomials:
(x + 2)(x – 3)
To multiply these, apply the distributive property:
- x * x = x²
- x * -3 = -3x
- 2 * x = 2x
- 2 * -3 = -6
The resulting product is:
x² – 3x + 2x – 6
Now, combine the like terms:
x² – x – 6
This is the simplified form of the product.
By following these steps, you can effectively multiply polynomials and simplify complex algebraic expressions, which is essential for solving more complicated problems involving algebraic fractions.
Division and Its Impact on Numerators
When performing operations that involve fractions, the effect of the operation on the numerator is critical to understand. The numerator plays a central role in determining the overall value of the fraction. When one quantity is placed in the numerator and another in the denominator, the impact of reducing or increasing these values can significantly alter the outcome of the expression. This is particularly relevant when the numerator is affected by division.
In fractional calculations, if the numerator is divided by a number, it can either decrease or simplify the expression, depending on the values involved. Understanding how to properly manage these changes in the numerator allows for the simplification of expressions, making it easier to perform further calculations or solve problems.
How Division Affects the Numerator
To better understand how the numerator is influenced, let’s consider an example:
| Initial Expression | Numerator After Division |
|---|---|
| 4x / 2 | 2x |
| (x + 3) / 5 | (x + 3)/5 (no change) |
| 6a / 3b | 2a / b |
As shown, when division occurs, the numerator’s value is altered. In the first example, 4x / 2 becomes 2x. In the second example, (x + 3) / 5 remains the same, showing no change in the numerator. The third example illustrates how both the numerator and denominator can be reduced in a way that simplifies the fraction.
By understanding the impact of division on the numerator, it becomes easier to simplify fractions, allowing for more efficient problem-solving. Each operation must be approached with care to ensure that the fraction is simplified to its lowest terms.
Practice Problems with Step-by-Step Solutions
To master any mathematical concept, practicing various problems with clear solutions is essential. In this section, we will explore a series of examples that demonstrate how to work through each problem in a logical, systematic manner. By breaking down each step, you will gain a deeper understanding of how operations interact within fractional forms and how to simplify or manipulate them effectively.
Problem 1: Simplifying a Fraction
Let’s begin with a simple fraction and simplify it step by step:
Problem: Simplify the fraction 8x / 4.
- Start by examining the numerator and the denominator.
- Identify that both 8 and 4 can be divided by 4.
- Divide both the numerator and the denominator by 4.
- The simplified form of 8x / 4 becomes 2x.
Thus, the simplified fraction is 2x.
Problem 2: Handling a Complex Fraction
Now let’s tackle a more complex problem involving both a numerator and denominator with additional terms:
Problem: Simplify (6x + 3) / 3.
- Observe that both terms in the numerator, 6x and 3, have a common factor of 3.
- Factor out 3 from the numerator: 3(2x + 1) / 3.
- Now, cancel the common factor of 3 from the numerator and the denominator.
- The simplified fraction is 2x + 1.
So, the result is 2x + 1.
By following step-by-step solutions like these, you can gain confidence in handling various problems involving fractions and their simplification. The key is to break down each step, making sure each operation is performed correctly to achieve the simplest possible result.