Lesson 6.2 Practice Properties of Parallelograms Answer Key
In this section, we will delve into the essential aspects of a special class of quadrilaterals, focusing on their defining features and how to solve related problems. By studying these figures, you will gain a deeper understanding of their characteristics and how they relate to other shapes in geometry.
As we explore the relationships between sides, angles, and diagonals, this guide will provide step-by-step solutions to help you master the concepts. The aim is to offer clear, structured explanations and techniques that will support your learning and enhance your problem-solving skills in geometry.
Lesson 6.2 Practice Answer Key Overview
This section provides a comprehensive guide to solving problems related to a specific type of quadrilateral. By reviewing the solutions, you will gain clarity on key geometric principles and how to apply them effectively. The goal is to enhance your understanding of the fundamental concepts that govern the relationships between sides, angles, and diagonals.
Understanding the Key Concepts

To successfully navigate through the challenges, it’s important to grasp the main characteristics that define these geometric figures. This includes understanding how their sides and angles behave under certain conditions, as well as recognizing how to manipulate coordinates and apply formulas correctly. The practice problems are designed to reinforce these concepts and improve your problem-solving abilities.
Step-by-Step Solution Breakdown
The solutions are structured to provide a clear, logical progression through each problem. Starting with identifying known variables and applying the correct geometric principles, you will move toward solving the problem with precision. By following this approach, you will not only find the correct solutions but also strengthen your overall grasp of geometric reasoning.
Understanding Parallelogram Properties

In this section, we focus on the fundamental characteristics of a specific type of quadrilateral, emphasizing how its sides, angles, and diagonals interact. Mastering these key aspects is essential for solving related geometric problems effectively. By recognizing these features, you can apply various geometric principles to analyze and work with these shapes.
Key Characteristics of the Shape
The defining features of this geometric figure include the relationships between its opposite sides and angles. Understanding these connections is crucial for solving problems accurately. The main attributes to keep in mind are:
- Opposite sides are equal in length – This means both pairs of opposing sides are congruent, providing a balanced structure.
- Opposite angles are equal – The angles opposite each other are always of the same measure.
- Consecutive angles are supplementary – Any two adjacent angles will add up to 180 degrees.
- Diagonals bisect each other – The diagonals intersect at their midpoints, dividing each into two equal parts.
How to Apply These Concepts
Now that you are familiar with the key features, it is essential to understand how to use them in problem-solving scenarios. Here are a few tips:
- Start by identifying pairs of opposite sides and angles when given a figure.
- Use the properties of supplementary angles to find unknown angles in the shape.
- Leverage the diagonal bisection property to find midpoints and calculate lengths.
- Apply these relationships to solve for missing variables and verify geometric solutions.
Mastering these core characteristics will help you approach any related geometry problem with confidence and accuracy.
Key Concepts in Parallelogram Practice

In this section, we will focus on the essential concepts needed to solve problems related to a specific type of quadrilateral. These concepts will guide you through various challenges and help you understand how different geometric properties are interrelated. Mastery of these principles will provide you with the necessary tools to approach problems confidently and accurately.
Core Geometric Ideas
To work effectively with this particular shape, it’s important to understand the core geometric properties that define it. The following concepts are essential:
- Side Relationships – Opposite sides are congruent, which means they are equal in length.
- Angle Relationships – Opposite angles are equal, while consecutive angles are supplementary, adding up to 180 degrees.
- Diagonal Interactions – The diagonals bisect each other, meaning they intersect at their midpoints and divide the shape into smaller, congruent triangles.
- Symmetry and Balance – The shape maintains symmetry, where each half is a mirror image of the other.
Practical Applications and Problem-Solving
Once you grasp these concepts, the next step is applying them to solve specific problems. Here are some useful strategies:
- Identify the parallel sides and angles in any given figure.
- Use the property of congruent sides to find missing lengths.
- Leverage angle relationships to calculate unknown angles within the shape.
- Apply diagonal bisection to find the midpoints and solve for unknown distances.
These strategies will enable you to approach various problems more systematically and effectively, ensuring a deeper understanding of the figure’s properties and their applications in geometry.
Step-by-Step Solutions for Lesson 6.2
This section provides a detailed breakdown of solving problems related to a specific quadrilateral. By following each step carefully, you can better understand how geometric properties are applied to find solutions. The goal is to walk you through the process, highlighting key concepts and offering clear guidance on how to approach similar problems independently.
The solutions provided here follow a logical sequence, starting with the identification of known values and moving toward solving for unknown variables. Each step is explained thoroughly to ensure clarity and to help reinforce important geometric principles.
Start by reviewing the figure and noting all given information. Next, apply the relevant properties of the shape to determine relationships between sides, angles, and diagonals. Finally, solve the equations or use geometric formulas to find missing values. By practicing these steps, you’ll become more comfortable with the process and improve your problem-solving skills.
What Are Parallelogram Sides?
The sides of a specific type of quadrilateral play a crucial role in defining its shape and structure. Understanding the relationships between these sides is key to solving geometric problems involving this figure. These sides are not just simple line segments; they have particular characteristics that distinguish them from other shapes.
In this shape, opposite sides are congruent, meaning they have equal length. Additionally, these sides are parallel, which means they never meet, no matter how far they are extended. This parallelism creates a balance and symmetry within the figure that is essential for its geometric properties.
Recognizing these fundamental characteristics allows you to use them effectively in solving for unknown side lengths or angles. By applying these principles, you can easily navigate through problems that involve the sides of this quadrilateral and gain a deeper understanding of its structure.
Angles in Parallelograms Explained
The angles within a particular type of quadrilateral are integral to understanding its geometry and solving related problems. These angles exhibit specific relationships that can be used to determine unknown values, making them a key element in solving geometric equations involving this shape.
Opposite Angles Are Equal
One of the fundamental properties of this figure is that opposite angles are always equal in measure. This means that when you identify one angle, you automatically know the value of its opposite angle. For example, if one angle is 70°, the angle directly opposite it will also be 70°.
Consecutive Angles Are Supplementary
Another important rule is that consecutive angles, or angles that share a side, are supplementary. This means that the sum of two adjacent angles is always 180°. If you know the measure of one angle, you can easily find the other by subtracting from 180°. For example, if one angle is 120°, the adjacent angle must be 60° to satisfy this condition.
Understanding these relationships helps you work through geometric problems more effectively, especially when you are tasked with finding missing angle measures or solving for other unknown variables within the figure.
Using Coordinates to Identify Parallelograms

In this section, we will explore how to use coordinates to determine whether a given quadrilateral is of a specific type. By analyzing the positions of the vertices on the coordinate plane, you can apply geometric principles to verify if the shape exhibits the characteristics needed for identification.
One of the most effective ways to identify this type of quadrilateral is by checking the slopes of its sides. If both pairs of opposite sides have equal slopes, the shape is guaranteed to be the figure we are focusing on. Additionally, you can calculate the lengths of these sides using the distance formula to confirm that the opposite sides are congruent.
To apply this method, follow these steps:
- Plot the coordinates of the vertices on the graph.
- Use the slope formula to find the slopes of the sides.
- If opposite sides have the same slope, they are parallel.
- Use the distance formula to ensure opposite sides have equal length.
By using these coordinate-based methods, you can confidently determine if a quadrilateral meets the criteria for the shape you’re examining.
How to Prove Parallelogram Properties
Proving the characteristics of a specific type of quadrilateral requires a systematic approach that involves understanding its geometric relationships. There are several methods to demonstrate these properties, from using basic principles of parallel lines to leveraging congruency and symmetry in the shape’s sides and angles. By proving these properties, you can establish the validity of the figure’s classification and solve related problems effectively.
One common technique is to use congruence and parallelism properties to show that opposite sides are equal and parallel. Additionally, proving that diagonals bisect each other can also be a powerful tool in confirming the shape’s properties. Each method uses logical steps to connect the figure’s features and provide mathematical justification for its classification.
Here are some key steps to prove these properties:
- Step 1: Show that opposite sides are congruent. Use the distance formula to measure and compare side lengths.
- Step 2: Prove that opposite sides are parallel. Use the slope formula to compare the slopes of opposite sides.
- Step 3: Demonstrate that the diagonals bisect each other. Calculate the midpoints of both diagonals and verify they are the same point.
- Step 4: Show that consecutive angles are supplementary. Measure angles using geometric properties and verify their sum equals 180°.
By following these steps, you can systematically prove the key features of the figure and deepen your understanding of its geometric nature.
Common Mistakes in Parallelogram Problems
When solving problems related to a specific type of quadrilateral, it’s easy to make mistakes, especially if you’re not careful with certain geometric properties. Understanding the common pitfalls can help you avoid errors and solve problems more efficiently. Below, we outline some of the most frequent mistakes students make and provide tips on how to avoid them.
| Common Mistake | Explanation | How to Avoid |
|---|---|---|
| Incorrectly assuming all sides are equal | Not all sides of the figure are necessarily congruent, only opposite sides. Confusing this can lead to incorrect conclusions about side lengths. | Remember, only opposite sides are equal in length, not adjacent sides. |
| Forgetting to check parallelism | Some students forget that opposite sides must be parallel to classify the shape correctly. Simply knowing the side lengths is not enough. | Always check the slopes of opposite sides to ensure they are parallel. |
| Confusing diagonals | Diagonals in this figure bisect each other, but they are not necessarily equal in length. Mistaking this property can lead to incorrect conclusions. | Be sure to distinguish between bisected diagonals and those that are equal in length. |
| Ignoring angle relationships | Consecutive angles in this quadrilateral are supplementary, but students may forget to account for this when solving for unknown angles. | Remember that consecutive angles add up to 180°, so always check the sum of adjacent angles. |
By staying mindful of these common mistakes and applying the correct principles, you can enhance your problem-solving skills and approach geometric challenges with confidence.
How to Find Missing Angles

In geometry, solving for unknown angles is a common task, especially when working with shapes that have specific properties, such as parallel sides and equal angles. Finding missing angles typically involves understanding the relationships between adjacent and opposite angles. By applying basic geometric principles, such as the angle sum of a triangle or the fact that consecutive angles in certain figures are supplementary, you can easily calculate the unknown values.
Here’s a step-by-step guide on how to approach finding missing angles:
Step 1: Use Supplementary Angles
When two angles are adjacent to each other and share a common side, they are supplementary, meaning their sum is 180°. This property can help you find missing angles when only one angle is known.
Step 2: Use Opposite Angles
When dealing with intersecting lines or diagonals, opposite angles (also known as vertical angles) are always congruent. If one angle is known, the opposite angle is always the same.
| Known Angles | Formula | Missing Angle |
|---|---|---|
| Adjacent angles (sum = 180°) | Angle 1 + Angle 2 = 180° | Angle 2 = 180° – Angle 1 |
| Opposite angles (congruent) | Angle 1 = Angle 2 | Angle 2 = Angle 1 |
By using these relationships, you can systematically solve for missing angles in a variety of geometric problems. Ensure that you double-check the angle types and the relationships between them before applying any formulas.
Perimeter and Area of Parallelograms
Calculating the perimeter and area of quadrilaterals with specific geometric properties is essential in understanding their size and shape. The formulas for finding the perimeter and area of this particular type of quadrilateral are straightforward but require careful attention to the dimensions. These measurements are based on the lengths of the sides and the height, which are key components in the formula derivation.
Perimeter Calculation
The perimeter of a quadrilateral is the total length of all its sides. For figures with opposite sides that are equal, the perimeter is simply the sum of the lengths of all four sides. The formula for the perimeter can be expressed as:
- Perimeter = 2 × (Base + Side)
In this case, the “Base” refers to the length of one side, and the “Side” refers to the length of the other adjacent side. Since the opposite sides are congruent, this formula is enough to find the perimeter.
Area Calculation

To find the area of a quadrilateral, the formula involves the base and the height, where the height is the perpendicular distance from one side to the opposite side. The formula for area is:
- Area = Base × Height
Here, the “Base” is any one of the sides, and the “Height” is the vertical distance from that base to the opposite side. It’s important to use the perpendicular height, not the slant height, to ensure an accurate calculation of the area.
By understanding and applying these formulas, you can easily calculate the perimeter and area for any quadrilateral with these specific characteristics. Make sure to correctly identify the base and height, and use consistent units of measurement throughout the calculations.
Visualizing Parallelograms with Diagrams
Understanding geometric shapes can be greatly enhanced through visual representation. Diagrams offer a clear way to understand the relationships between the sides, angles, and other features of these shapes. Visualizing geometric figures helps break down complex problems and simplifies the process of solving them. By observing a diagram, you can immediately see how specific attributes like side lengths and angle measures relate to each other, aiding in faster and more accurate solutions.
For example, when working with figures where opposite sides are equal and parallel, a diagram can help you see the symmetry and properties that are essential for solving various types of problems. Below is a diagram showing some key features of a shape that meets these conditions:
| Feature | Explanation |
|---|---|
| Opposite sides | Equal in length and parallel |
| Angles | Opposite angles are equal; adjacent angles are supplementary |
| Diagonals | They bisect each other, but are not necessarily of equal length |
Diagrams help you better understand how these features work together to form the overall shape. By drawing or reviewing such illustrations, you gain a clearer, more intuitive understanding of the geometric principles at play, making it easier to solve related problems.
Advanced Techniques for Solving Problems
To master geometric challenges, it is essential to develop advanced problem-solving strategies that go beyond basic formulas and principles. These techniques involve a deeper understanding of relationships between different elements of shapes, as well as the ability to manipulate and combine various concepts to find solutions. By utilizing these methods, you can tackle more complex problems with confidence and precision.
One effective strategy is the use of coordinate geometry, which allows you to approach shape-related questions algebraically. By assigning coordinates to the vertices of a figure, you can apply distance, slope, and midpoint formulas to determine key properties such as side lengths and angles. This method is especially helpful for analyzing irregular shapes and deriving unknown values.
Another powerful technique is the use of transformations, such as rotation, reflection, and translation, to simplify problems. By applying these transformations to a given figure, you can gain insights into its symmetry and properties, making it easier to solve problems related to congruence, similarity, and parallelism.
In addition, breaking down complex problems into smaller, manageable parts is crucial. This method involves identifying sub-problems within the larger context and solving them step-by-step. This approach helps in avoiding errors and ensures that each part of the problem is addressed thoroughly, leading to a more accurate and efficient solution.
Relationship Between Diagonals and Angles
The connection between the diagonals of a shape and its internal angles is fundamental to understanding its geometry. Diagonals are line segments that connect non-adjacent vertices, and their behavior reveals key information about the shape’s structure. By studying how the diagonals interact with each other and with the angles of the figure, we can uncover properties that are crucial for solving geometric problems.
When diagonals intersect, they often create specific angle relationships. For example, in certain quadrilaterals, the diagonals may bisect each other at right angles, forming pairs of congruent angles. In other cases, the diagonals might not be perpendicular but still influence the interior angles in distinct ways. Understanding these relationships helps in solving for unknown angles or proving the congruence of certain parts of the shape.
- Congruence of Opposite Angles: In many shapes, the angles on either side of an intersecting diagonal are congruent. This symmetry can simplify calculations and proofs.
- Diagonal Bisection: Some figures, such as rectangles and rhombuses, have diagonals that bisect each other. This division can be used to find missing angle measures.
- Angle Sum Property: The sum of the interior angles of a shape remains constant, and the diagonals can help in identifying specific angle values by breaking the shape into smaller, more manageable parts.
Overall, understanding how diagonals relate to the angles of a figure is a key aspect of geometry, aiding in both theoretical exploration and practical problem-solving.
Real-World Applications of Parallelograms
The shape of parallelograms appears frequently in everyday life, often in areas where precise geometry is needed. These shapes, which have opposite sides parallel and equal in length, are more than just mathematical abstractions–they have practical applications across various fields. Understanding how these geometric figures are used in real-world situations can help us appreciate their value beyond the classroom.
Engineering and Architecture
In construction and design, parallelograms are often used to create stable and efficient structures. For example, trusses, which are used to support bridges and roofs, often rely on parallelogram-shaped elements. These shapes provide both strength and stability while allowing for efficient material use. Additionally, many architectural features, such as windows and door frames, may include parallelogram shapes for aesthetic appeal and structural integrity.
Art and Design
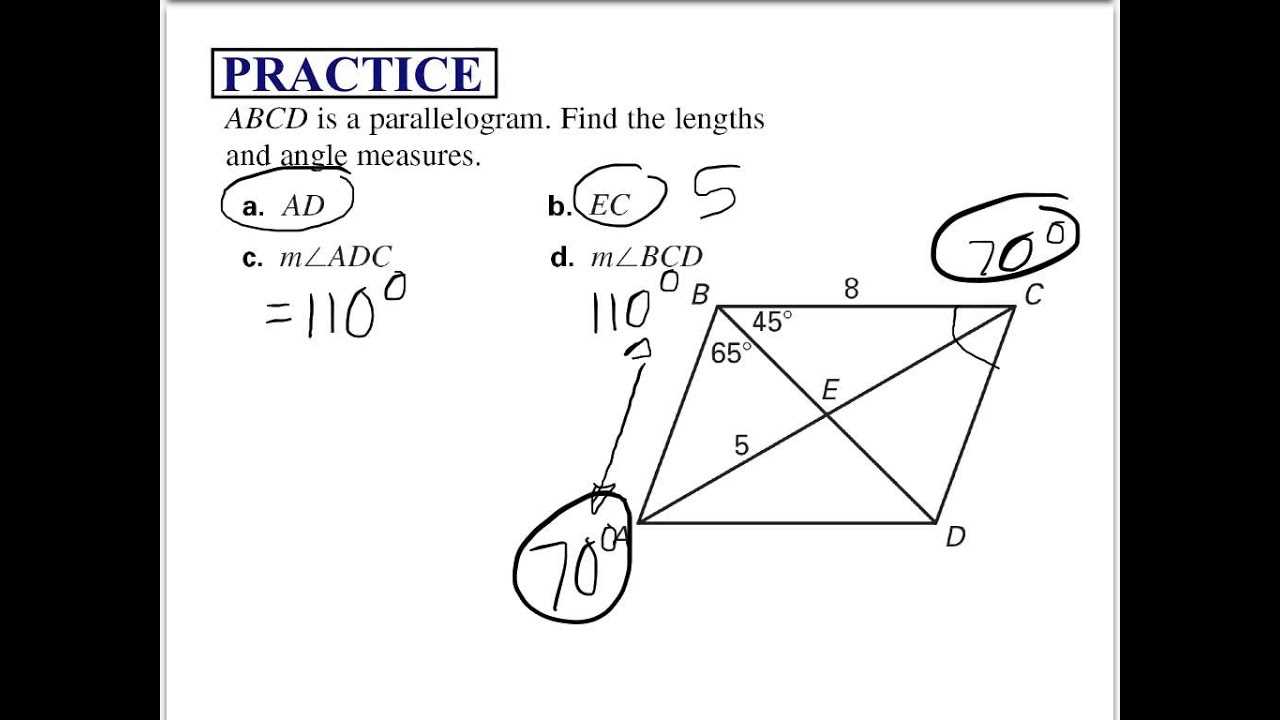
In the world of art and design, parallelograms help create visual balance and symmetry. Artists and designers often use these shapes to create patterns, textures, and structures that are both aesthetically pleasing and functional. Whether in graphic design, textiles, or even landscape planning, the properties of parallelograms help in achieving desired visual effects and spatial organization.
These real-world examples show how important the understanding of geometric shapes like parallelograms is in both practical and creative fields. The ability to recognize and apply their properties can lead to more efficient designs, better structures, and visually engaging creations.
Tips for Mastering Parallelogram Practice
Mastering the skills related to geometric shapes that feature opposite sides in parallel and equal lengths requires both understanding and consistent application. Success comes through focusing on key concepts and practicing regularly. Below are some essential tips to help you improve your ability to solve problems involving these shapes effectively.
Understand the Core Principles
Before diving into complex problems, make sure you fully understand the fundamental principles that govern the shape. This includes knowing the relationships between angles, side lengths, and diagonals. Here are a few things to keep in mind:
- Opposite sides are equal in length and parallel.
- Adjacent angles are supplementary, meaning their sum is 180°.
- Diagonals bisect each other, creating two equal parts.
Practice with Diagrams
Working with visual aids can significantly enhance your understanding. Try sketching out various figures and identifying key properties such as angles and side lengths. Some tips for better diagramming include:
- Label all angles and sides to avoid confusion.
- Use a protractor or ruler to ensure accuracy when drawing the shapes.
- Practice drawing the diagonals and measuring their lengths.
By integrating these techniques into your study routine, you will be able to confidently approach problems and improve your problem-solving skills over time.
Preparing for Parallelogram Geometry Tests
When preparing for exams focused on shapes with opposite sides equal and parallel, it’s crucial to master both theoretical concepts and practical problem-solving techniques. To ensure success, a strategic approach is needed, combining study, practice, and review of key principles related to these geometric figures. Below are some essential tips to help you efficiently prepare for your upcoming geometry test.
Focus on Key Concepts
Start by reviewing the fundamental properties of the shape. Understanding the relationships between angles, side lengths, and diagonals is essential for solving problems accurately. Pay close attention to the following:
- How opposite sides are congruent and parallel.
- The concept of supplementary adjacent angles.
- How the diagonals bisect each other and the impact this has on the shape’s symmetry.
Practice with Sample Problems
Work through a variety of example problems, focusing on both simple and complex scenarios. Ensure that you can apply the core principles to different situations. Some methods to improve your problem-solving skills include:
- Solving multiple practice tests to simulate the exam environment.
- Working on problems with varying levels of difficulty to build confidence and proficiency.
- Revisiting areas where you struggled, and practicing those concepts more intensively.
By following a consistent study routine and practicing regularly, you’ll be well-prepared to tackle any geometry test related to these specific shapes and their characteristics. Stay organized, focus on the basics, and continue honing your skills through repetition and review.