Algebra Chapter 6 Test Answers and Solutions

In this section, we dive into essential concepts and techniques that will help you navigate through complex mathematical problems. By understanding the core principles, you can approach challenges with greater confidence and efficiency. Whether you are dealing with equations, expressions, or word problems, knowing how to break down each part is crucial for success.

Comprehensive practice is an important tool in mastering these skills. Working through various exercises allows you to apply what you’ve learned, identify areas for improvement, and ultimately sharpen your problem-solving abilities. By reviewing step-by-step solutions, you can gain a deeper understanding of the methods used to arrive at the correct results.

In the following sections, we will explore practical tips and strategies to improve your performance. With consistent effort and the right approach, achieving mastery in this area is within your reach.

Algebra Chapter 6 Test Answers

In this section, we explore various solutions and methods to help you tackle the more challenging aspects of the mathematical problems you will encounter. By breaking down the steps, you can better understand how to approach and solve each problem. This will help build your confidence and sharpen your skills for similar exercises.

Key Problem-Solving Techniques

To succeed in solving these problems, it’s important to recognize patterns and apply the right formulas. Some problems may require rearranging terms or simplifying expressions, while others may need specific methods like substitution or factoring. By practicing a variety of problem types, you can develop a systematic approach that works for you.

Step-by-Step Solutions

Working through each solution step-by-step allows for better comprehension and retention of the material. Below is an example breakdown of typical problems and their corresponding solutions.

Problem	Step 1	Step 2	Solution
Example 1: Solve for x	Isolate the variable	Simplify the equation	x = 5
Example 2: Factor the expression	Identify common factors	Factor into binomials	(x – 2)(x + 3)
Example 3: Solve the system of equations	Use substitution method	Substitute values to find x and y	x = 3, y = 4

By following these steps and reviewing examples like the ones shown, you can refine your problem-solving process and be better prepared for future exercises.

Understanding Key Concepts in Chapter 6

Grasping the core ideas presented in this section is essential for tackling the more complex problems. By mastering the fundamentals, you can approach a wide range of exercises with confidence and clarity. These concepts are building blocks that will help you not only solve individual problems but also understand the broader mathematical relationships at play.

Throughout this section, we focus on understanding essential techniques such as manipulation of expressions, simplifying terms, and applying rules to different problem types. Mastering these areas will allow you to address problems efficiently and accurately.

Concept	Description	Application
Factoring	Breaking down expressions into simpler terms	Used to simplify equations and solve for variables
Equations	Mathematical statements showing equality	Finding unknown values by balancing both sides
Substitution	Replacing one variable with its equivalent	Used in solving systems of equations
Exponents	Representing repeated multiplication	Applied to simplify expressions and solve problems

By familiarizing yourself with these key concepts, you can begin to see patterns and develop a systematic approach to solving problems. Understanding the relationships between these ideas will allow for more efficient problem-solving in future exercises.

Common Mistakes in Algebra Tests

When solving mathematical problems, many learners make similar errors that can affect their results. Recognizing these common mistakes can help you avoid them in future exercises and improve your overall understanding of the material. By being mindful of these pitfalls, you can approach problems more strategically and reduce the chance of errors.

Some common mistakes often arise from misunderstanding basic principles or rushing through calculations without verifying the work. Below are several mistakes that frequently occur:

• Misunderstanding Order of Operations: Failing to follow the correct sequence when simplifying expressions can lead to incorrect results.
• Incorrectly Handling Negative Signs: Neglecting to distribute negative signs properly can cause sign errors in terms and final answers.
• Not Checking Solutions: Skipping the verification step after solving a problem can allow small errors to go unnoticed.
• Overlooking Special Cases: Certain problems may have exceptions, such as when dividing by zero or dealing with square roots of negative numbers.
• Misplacing Parentheses: Incorrect placement or omission of parentheses can drastically change the meaning of an equation or expression.

Being aware of these mistakes will help you focus on accuracy and clarity during problem-solving. By taking extra care with each step, you can minimize errors and improve your performance in similar exercises.

Step-by-Step Solutions for Practice Problems

To truly master mathematical concepts, it’s crucial to break down each problem into manageable steps. By carefully working through each stage, you not only arrive at the correct answer but also gain a deeper understanding of the methods used. This approach builds a solid foundation that helps with solving more complex problems in the future.

Below is an example of how to approach a typical problem. Each step is explained in detail to ensure clarity and comprehension, showing how to handle different aspects of the problem.

Example Problem: Solve for x: 3(x + 4) = 18

Step 1: Begin by expanding the equation. Use the distributive property to multiply 3 by both terms inside the parentheses.

3 * x + 3 * 4 = 18

This simplifies to: 3x + 12 = 18

Step 2: Next, isolate the variable by subtracting 12 from both sides of the equation.

3x + 12 – 12 = 18 – 12

This simplifies to: 3x = 6

Step 3: Finally, divide both sides by 3 to solve for x.

3x / 3 = 6 / 3

This gives: x = 2

By following each step carefully, we find that the solution to the equation is x = 2. Practicing this approach with various problems will help you develop a reliable method for solving similar equations in the future.

How to Tackle Word Problems Effectively

Word problems can often seem overwhelming due to their complex nature and the need to translate real-world situations into mathematical expressions. However, by breaking the problem down into smaller, more manageable parts, you can approach these types of questions with clarity and confidence. The key is to identify the relevant information and translate it into a form that you can work with.

Step 1: Read the problem carefully. It’s essential to understand the context and what the problem is asking. Look for key terms such as “total,” “difference,” “product,” and “quotient,” which can guide you toward the right operations.

Step 2: Identify the variables. Determine what the unknowns are in the problem and assign a letter or symbol to represent them. This helps in organizing the information and forming the equation.

Step 3: Translate the words into an equation. Take the information you’ve gathered and express it mathematically. This might involve addition, subtraction, multiplication, or division, depending on the problem.

Step 4: Solve the equation. Once you have your equation, proceed with solving it as you would with any other mathematical problem. Be sure to check your work at each step to ensure accuracy.

Step 5: Interpret the result. After solving the equation, make sure the answer makes sense in the context of the problem. If necessary, review the question again to confirm that you have answered what was asked.

By following these steps, you can simplify complex word problems and approach them with a clear strategy. Practice is essential in becoming proficient, so regularly working through different types of word problems will increase your confidence and skill in tackling them effectively.

Test Strategies for Algebra Chapter 6

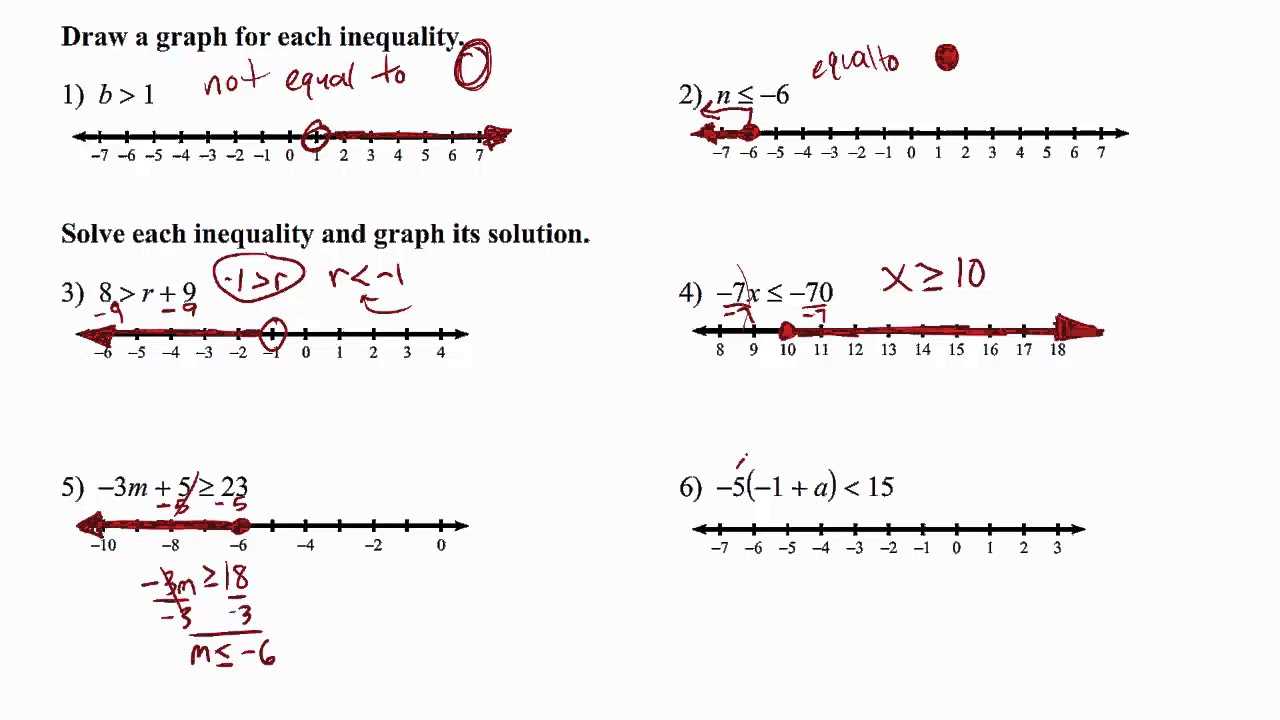
Approaching an exam with a well-thought-out strategy can significantly improve your performance. Knowing how to prioritize, manage time, and tackle different types of problems will help you maximize your results. In this section, we’ll explore effective methods to enhance your approach when facing similar exercises.

By adopting the right strategies, you can approach each problem more efficiently, ensuring that you spend your time wisely and avoid unnecessary mistakes. Here are some key strategies to keep in mind:

• Understand the Structure: Familiarize yourself with the types of questions likely to appear. This allows you to mentally prepare and know what to expect.
• Start with Familiar Problems: Begin with problems that you feel confident about. This helps build momentum and can give you a quick win before tackling more complex questions.
• Use Process of Elimination: If faced with multiple-choice questions, eliminate clearly incorrect answers first. This increases the chances of selecting the correct option.
• Break Down Complex Problems: For more challenging exercises, break them into smaller steps. This makes it easier to manage and ensures you don’t miss any critical parts.
• Check Your Work: If time allows, go back and double-check your solutions. Small errors in calculations or signs can lead to incorrect answers.

With practice, these strategies will become second nature. Regularly reviewing key concepts, working through sample problems, and using time management techniques will help you approach any exercise with confidence and efficiency.

Tips for Reviewing Chapter 6 Material

Effective revision is crucial for reinforcing the concepts learned and ensuring that you are fully prepared for any upcoming exercises. Instead of passively reading through the material, engaging with it actively will help you retain key information and solve problems with greater accuracy. The goal is to revisit and practice critical topics in a way that solidifies your understanding.

Here are some practical tips for reviewing the material efficiently:

• Summarize Key Concepts: Create brief notes or flashcards highlighting important rules, methods, and formulas. Reviewing these will help you recall essential information quickly during problem-solving.
• Practice with Examples: Solve a variety of practice problems, especially those you found challenging. This helps reinforce your knowledge and identify areas that may need further attention.
• Teach What You’ve Learned: Explaining concepts to someone else, or even to yourself, can deepen your understanding. It forces you to organize your thoughts and clarify any areas of confusion.
• Use Visual Aids: Diagrams, charts, and graphs can help visualize abstract concepts and improve comprehension. They are especially useful for problems involving geometry or relationships between variables.
• Review Mistakes: Look over your past errors and try to understand why you made them. This will prevent you from repeating the same mistakes and help you recognize similar patterns in future problems.

By following these review strategies, you can approach your studies with purpose and maximize your retention. Consistency and active engagement with the material are key to mastering the content effectively.

Mastering Algebraic Equations and Expressions

To become proficient in solving mathematical problems, it’s essential to fully understand the structure and manipulation of equations and expressions. These tools form the foundation for solving a wide range of problems, from basic calculations to more complex applications. Mastery over these concepts allows you to work through equations more efficiently and with greater confidence.

Step 1: Begin by familiarizing yourself with the different forms of equations and expressions. An equation often involves variables and constants set equal to one another, while an expression includes terms that can be simplified or evaluated without an equality sign.

Step 2: Understand the operations involved. The basic operations–addition, subtraction, multiplication, and division–are often the building blocks for simplifying expressions or solving equations. Recognizing when and how to apply each operation is crucial to progressing through the problem.

Step 3: Master the art of balancing equations. This involves isolating the variable by performing inverse operations on both sides of the equation. Each step should maintain the equality, ensuring the equation remains balanced while you solve for the unknown.

Step 4: Practice simplifying complex expressions. This includes combining like terms, using distributive properties, and factoring when necessary. By recognizing common patterns, you can simplify problems and make the solving process much easier.

Step 5: Work with word problems that require translating real-life situations into mathematical language. These problems help strengthen your ability to set up the correct equations and identify which operations to use in each scenario.

With consistent practice and a clear understanding of these steps, you will develop a strong command over equations and expressions. This will serve as the foundation for solving more advanced problems with ease and accuracy.

Improving Problem Solving Skills

Enhancing your problem-solving abilities is key to mastering any type of mathematical challenge. Whether you’re faced with simple calculations or more intricate scenarios, refining your approach will help you find solutions more effectively. By developing a systematic process, you can tackle problems with confidence and precision.

Build a Strong Foundation

Before attempting any problem, ensure that you have a solid understanding of the basic concepts involved. A clear grasp of foundational principles allows you to recognize patterns and apply the right techniques when needed. Review essential rules and operations to strengthen your overall knowledge.

Follow a Structured Approach

Step 1: Identify the problem and gather all necessary information. Carefully read through the question to understand what is being asked. It’s important to break the problem into smaller parts and address each one individually.

Step 2: Choose the appropriate strategy. Depending on the type of problem, decide whether you need to simplify expressions, isolate variables, or apply specific mathematical operations. Try multiple methods if necessary to find the most efficient solution.

Step 3: Implement your strategy and solve the problem step by step. Keep your work organized, and show each intermediate step to avoid mistakes. This makes it easier to check your work later on and track down any errors.

Step 4: Review your solution. After finding an answer, take the time to verify its accuracy. Ask yourself if the result makes sense in the context of the problem and if all steps were followed correctly.

By practicing these strategies consistently, you will develop the skills necessary to approach problems systematically, leading to quicker and more reliable solutions. Strengthening these skills over time will make problem-solving more intuitive and efficient.

How to Handle Multiple Choice Questions

Multiple-choice questions can be challenging, but with the right approach, you can effectively increase your chances of selecting the correct answer. These questions often offer a set of possible answers, and your task is to identify the best choice. Understanding how to navigate these questions will help you think critically and use your time efficiently during assessments.

Key Strategies for Answering

One of the first things to remember when approaching multiple-choice questions is to carefully read both the question and all the options. Rushing through these questions can lead to simple mistakes. Here are some strategies to help you:

• Eliminate Clearly Wrong Options: Start by eliminating answers that are obviously incorrect. This increases your odds of choosing the correct one from the remaining options.
• Look for Clues in the Question: Often, the question itself contains hints that can help you narrow down the choices. Pay close attention to keywords or numbers that might guide you to the right answer.
• Consider All Options: Even if you think you know the answer right away, make sure to review all the choices. There may be more than one seemingly correct option, and a deeper analysis can reveal the best one.
• Check for Similar Answers: Sometimes, multiple answers will appear similar but with slight differences. Compare these options carefully to choose the one that fits best.
• Don’t Overthink: Trust your initial instincts. If you’re unsure between two answers, and one of them is a more straightforward choice, go with that one.

Example Question Breakdown

Let’s apply these strategies to an example question:

Question	Choices
What is the value of x in the equation 2x + 5 = 15?	A) 2 B) 5 C) 10 D) 7

First, eliminate any obviously incorrect choices. In this case, options A and D are unlikely to be correct, given the equation. After simplifying the equation, you’ll find that the correct value for x is 5, so the answer is B.

By following these strategies, you can approach multiple-choice questions more confidently and efficiently, improving your chances of selecting the right answers. Practice with a variety of problems, and over time, you’ll develop a sharper, more systematic approach to these questions.

Breaking Down Complex Algebraic Steps

When solving intricate mathematical problems, it’s easy to feel overwhelmed by the complexity of the steps involved. However, breaking down these steps into smaller, manageable parts can help you approach the problem with clarity and confidence. By understanding the logic behind each operation and following a structured process, you can simplify even the most challenging problems.

Step-by-Step Approach

To effectively tackle complex problems, it’s important to break them down into smaller, sequential tasks. This approach allows you to focus on one part of the problem at a time and reduces the risk of errors. Here’s how to start:

• Identify the goal: Before jumping into calculations, clearly define what you’re trying to solve. Understanding the end goal ensures you stay focused on the right approach.
• Isolate the variable: If the problem involves solving for a specific unknown, begin by isolating the variable. This often involves applying inverse operations to both sides of the equation.
• Simplify expressions: Break down more complicated expressions step by step. Combine like terms, distribute constants, or factor expressions where applicable.
• Apply the appropriate operations: Based on the problem, choose the right operations (such as addition, multiplication, or factoring) and apply them systematically to each part of the equation.

Practice Example

Consider the following problem: Solve for x in the equation 3x + 5 = 20.

• Step 1: Subtract 5 from both sides: 3x = 15.
• Step 2: Divide both sides by 3: x = 5.

By breaking down the problem into smaller, logical steps, you can more easily understand the underlying principles and reach the correct solution.

With practice, this method of dividing problems into smaller steps becomes second nature, enabling you to tackle even the most complex problems with confidence.

Identifying Key Topics for Your Test

When preparing for any assessment, focusing on the most important concepts is crucial for efficient study. Identifying the key topics ensures that you’re not overwhelmed by irrelevant material and can target your efforts where they will have the most impact. By recognizing patterns in the types of questions asked and the areas covered, you can better allocate your time and energy to the most critical parts of your preparation.

Focus on Commonly Tested Concepts

In most cases, exams tend to emphasize certain topics over others. By reviewing past assessments and identifying which areas were frequently covered, you can prioritize these for your study sessions. Some key topics to look out for include:

• Fundamental operations: These often serve as the building blocks for more complex problems. Ensuring you have a solid grasp on basic operations will help you solve more advanced questions with ease.
• Word problems: These types of questions require you to apply your knowledge to real-life scenarios, testing your ability to interpret and solve practical challenges.
• Equations and inequalities: Being comfortable with setting up, solving, and interpreting different types of equations is essential for success.
• Graphing skills: Understanding how to plot and interpret graphs is frequently tested, particularly in problems involving linear relationships and patterns.

Use Study Resources Wisely

In addition to reviewing previous exams, make use of study guides, practice problems, and textbooks that cover the key topics you’re most likely to encounter. These resources will not only reinforce your understanding of critical concepts but also help you identify any areas where you may need additional practice.

By focusing your attention on the most frequently tested concepts and utilizing available resources, you can approach your preparation more effectively and enter the assessment with confidence.

Best Resources for Algebra Chapter 6

When preparing for a challenging set of mathematical problems, selecting the right study resources can make all the difference. From interactive online platforms to comprehensive textbooks, there are numerous tools available to help solidify your understanding of key concepts. By using a variety of materials that suit your learning style, you can improve both your comprehension and problem-solving abilities.

Online Platforms and Tutorials

Interactive websites and online tutorials offer a dynamic way to review material and practice solving problems. These platforms often provide step-by-step solutions, quizzes, and video lessons that allow for a more engaging learning experience. Some of the best options include:

• Khan Academy: Known for its free, high-quality video tutorials and practice exercises, Khan Academy covers a wide range of topics and offers in-depth explanations.
• Wolfram Alpha: This computational engine allows you to input problems and receive detailed solutions, showing the steps involved in arriving at the answer.
• Brilliant: Brilliant offers interactive courses that focus on problem-solving and understanding concepts through real-world applications.

Textbooks and Study Guides

Textbooks remain one of the most reliable resources for in-depth explanations of concepts. They often provide a structured approach to learning, with plenty of examples and practice problems. Some popular options include:

• “Precalculus” by James Stewart: This textbook covers a wide array of topics and offers clear explanations, along with plenty of exercises to reinforce your learning.
• Study.com Guides: These concise study guides offer quick summaries of concepts, along with practice questions to test your knowledge.
• Scholastic Math Workbooks: Scholastic offers targeted workbooks for various skill levels, with practice questions designed to help you hone your problem-solving techniques.

Using a combination of these resources can help you better understand the material, practice consistently, and feel more confident heading into your assessment.

How to Manage Test Time Efficiently

Effective time management during assessments is crucial to ensure you complete all the questions within the given time frame while maintaining accuracy. With proper planning and strategy, you can maximize your performance and avoid rushing through problems. Developing a systematic approach helps reduce anxiety and increases your ability to focus on solving each question carefully.

Pre-Test Preparation

Before the assessment begins, it’s essential to set yourself up for success. Proper preparation can significantly influence how you approach the time constraints during the test:

• Familiarize Yourself with the Format: Know the types of questions (multiple choice, short answer, long problems) so you can allocate time accordingly.
• Practice Time Management: Complete practice questions under timed conditions to get used to the pressure of answering quickly yet accurately.
• Plan for Difficult Sections: If certain sections tend to be more challenging, plan to spend slightly more time on them, but avoid overthinking.

During the Test

Once the assessment begins, managing your time effectively is essential to ensure you get through all questions without rushing at the end:

• Start with What You Know: Begin with the questions you feel most confident about. This builds momentum and boosts your confidence.
• Use the Process of Elimination: For multiple-choice questions, eliminate obviously incorrect answers to increase your chances of selecting the correct one quickly.
• Set Time Limits for Each Section: Give yourself a specific amount of time for each section and stick to it. If a question is taking too long, move on and return to it later.
• Review Your Work: If time permits, quickly review your answers to catch any errors or missed questions.

By using these time-management strategies, you can approach your assessments with a clear plan, avoid unnecessary stress, and ensure that you give yourself the best chance to perform well.

Common Algebraic Terms to Know

In mathematics, understanding the terminology is crucial for solving equations and interpreting problems accurately. Familiarizing yourself with key terms will help you navigate through complex problems with confidence. Below are some fundamental concepts that you should be comfortable with, as they are often used across various types of questions.

Key Terms for Equations

When working with mathematical expressions and operations, recognizing and understanding certain terms can simplify the problem-solving process:

• Variable: A symbol (often a letter) that represents an unknown value in an equation or expression, such as x or y.
• Constant: A fixed value that does not change. It is usually represented by a number, such as 5 or -3.
• Coefficient: A numerical factor that multiplies the variable in a term, such as the 3 in 3x.
• Expression: A mathematical phrase that can contain variables, constants, and operators, but does not have an equality sign. For example, 2x + 5.

Operations and Relationships

Along with understanding individual terms, it is important to grasp the fundamental operations and relationships between them:

• Equation: A mathematical statement that shows two expressions are equal, typically involving an unknown variable. An example is 2x + 3 = 7.
• Expression Simplification: The process of reducing an expression to its simplest form, such as combining like terms or factoring.
• Exponents: The operation of raising a number to a certain power, indicated by a superscript, such as 2^3 = 8.
• Linear Equation: An equation that represents a straight line when graphed, typically in the form y = mx + b.

By mastering these terms and their meanings, you’ll be better equipped to approach problems and develop a solid understanding of mathematical concepts. Regular practice with these key ideas will significantly improve your ability to solve a wide range of problems efficiently and accurately.

Using Practice Tests for Preparation

Engaging in simulated assessments is an excellent way to assess your readiness and identify areas where improvement is needed. By completing practice exercises, you can build confidence, become familiar with the format of questions, and sharpen your problem-solving skills. These activities serve as a valuable tool for reinforcing your knowledge and fine-tuning your approach to various types of problems.

Benefits of Practice Exercises

Utilizing practice materials provides several advantages that enhance your preparation:

• Familiarity with Question Format: Practice assessments often mimic the actual exam structure, helping you become accustomed to the types of questions you will face.
• Time Management: Practicing under timed conditions helps you develop strategies to manage your time effectively during the actual evaluation.
• Identifying Weak Areas: Regular practice enables you to pinpoint specific topics or concepts that require further attention, allowing you to focus on your weaker points.
• Building Confidence: Completing practice exercises boosts your confidence and reduces anxiety, ensuring you’re mentally prepared for the real assessment.

How to Maximize the Use of Practice Tests

To get the most out of practice sessions, follow these strategies:

• Start Early: Begin practicing well in advance to give yourself enough time to address challenging areas and reinforce key concepts.
• Review Mistakes: After completing each practice set, take time to thoroughly review your errors. Understanding why you got a question wrong is essential to improving your skills.
• Simulate Real Conditions: Try to replicate actual testing conditions by setting a timer and eliminating distractions. This will help you get comfortable with the pressure of completing tasks within a set time.
• Track Progress: Keep a record of your practice sessions and results to track your improvement over time. This will give you insight into your readiness and highlight areas needing more focus.

By consistently using practice materials, you can enhance your problem-solving abilities, build stronger retention, and approach your upcoming evaluation with greater assurance.

Boosting Confidence Before the Test

Preparing for an important evaluation can often cause feelings of stress and self-doubt. However, building confidence in your abilities is crucial for performing at your best. By employing strategies that focus on mental preparation, you can approach the assessment with a positive mindset and a calm demeanor. Confidence not only improves performance but also reduces anxiety, allowing you to tackle challenges with clarity and focus.

Effective Techniques to Build Confidence

Here are some practical steps to help you enhance your confidence before the big day:

• Positive Visualization: Spend a few minutes visualizing yourself successfully completing the evaluation. This mental exercise can help set a confident tone and reduce nervousness.
• Practice Self-Affirmations: Remind yourself of your strengths and past successes. Repeating positive statements like “I am well-prepared” can help shift your mindset towards success.
• Review Your Progress: Take a moment to reflect on how much you’ve learned and the progress you’ve made. Acknowledging your hard work reinforces your belief in your abilities.
• Rest and Relaxation: Ensure you get a good night’s sleep before the evaluation. Rest is crucial for both mental clarity and emotional balance, helping you to perform at your peak.

Maintaining Calm and Focus During the Assessment

Once the evaluation begins, staying calm and focused is key to success. Here are some tips to keep your nerves in check:

• Stay Positive: If you encounter a difficult question, don’t panic. Approach it with a problem-solving mindset and remind yourself that you’ve prepared for this.
• Control Your Breathing: Deep breathing exercises can help calm your nerves and refocus your mind. Taking slow, deliberate breaths can help reduce anxiety and maintain concentration.
• Trust Your Preparation: Remember, the work you’ve put in leading up to this point has equipped you with the skills needed to succeed. Trust yourself and your abilities.

By using these techniques, you can boost your confidence, reduce stress, and approach the evaluation with a clear, focused mind. Confidence is key, and with the right mindset, you will be able to perform to the best of your ability.

Final Review Tips for Chapter 6

As the evaluation approaches, it’s essential to ensure your preparation is solid and that you’re ready to approach the material with confidence. A final review can help consolidate your understanding and sharpen your problem-solving abilities. This is your chance to go over key concepts, practice application, and address any lingering uncertainties before the big day. With a strategic approach, you can maximize your retention and tackle the assessment with clarity.

Key Focus Areas

During the final review, it’s important to revisit the main concepts and formulas that you’ll likely encounter. Here are some focal points to guide your last-minute preparations:

• Review Core Concepts: Go over the foundational principles that were covered throughout the material. Ensure you understand the basic formulas and how they apply in different scenarios.
• Practice with Examples: Work through sample problems and exercises. This not only reinforces what you’ve learned but also boosts your confidence in applying the concepts to real-life problems.
• Identify Weak Areas: Focus on sections that you found more challenging. Take extra time to work through any difficulties to ensure you’re comfortable with all material.
• Review Mistakes: Go over any errors you made in previous exercises or practice sessions. Understanding why you got something wrong is often just as valuable as practicing the right solutions.

Practical Strategies for the Final Hours

In the last few hours before the evaluation, adopting efficient study strategies can help you stay focused and relaxed:

• Do a Quick Overview: Skim through your notes or key sections, focusing on summaries and highlighted material. This refreshes your memory on essential topics.
• Stay Organized: Make sure all your materials–notes, formulas, practice questions–are neatly organized. A clutter-free study environment helps maintain focus.
• Practice Time Management: During your final review, simulate the timing of the evaluation. Practice solving problems within the set time frame to ensure you’re not rushed during the real thing.
• Stay Calm and Confident: Confidence plays a major role in your performance. Believe in the preparation you’ve done and stay positive. Stressing out will only hinder your ability to recall information clearly.

By focusing on these strategies and giving yourself a solid final review, you can enter the evaluation feeling prepared and confident. Trust in your preparation, and you’ll be able to perform at your best.