Springboard Algebra 1 Answer Key for All Levels

For students navigating through introductory mathematical courses, having access to a reliable resource for checking and understanding solutions is crucial. This guide provides a thorough overview of various problem-solving techniques and strategies designed to clarify complex concepts. Whether you’re tackling simple equations or more intricate functions, this collection of solutions serves as an invaluable tool for enhancing comprehension.
Effective study tools are essential for mastering the challenges presented in any curriculum. With clear explanations and step-by-step breakdowns, learners can gain confidence in their abilities. By reviewing each solution carefully, students can better grasp the underlying principles, making it easier to apply these concepts in future problems.
Building a strong foundation in basic mathematical principles is the key to success in higher-level topics. This resource is intended not only to provide answers but also to facilitate deeper understanding and promote independent problem-solving skills.
Springboard Algebra 1 Answer Key Overview
This section provides a comprehensive review of the solutions for the exercises in a foundational mathematics course. Designed to support students in reviewing their work, the guide helps ensure that learners can verify their answers and understand the reasoning behind each solution. With a clear breakdown of methods and results, this resource serves as a crucial aid for those looking to strengthen their problem-solving skills.
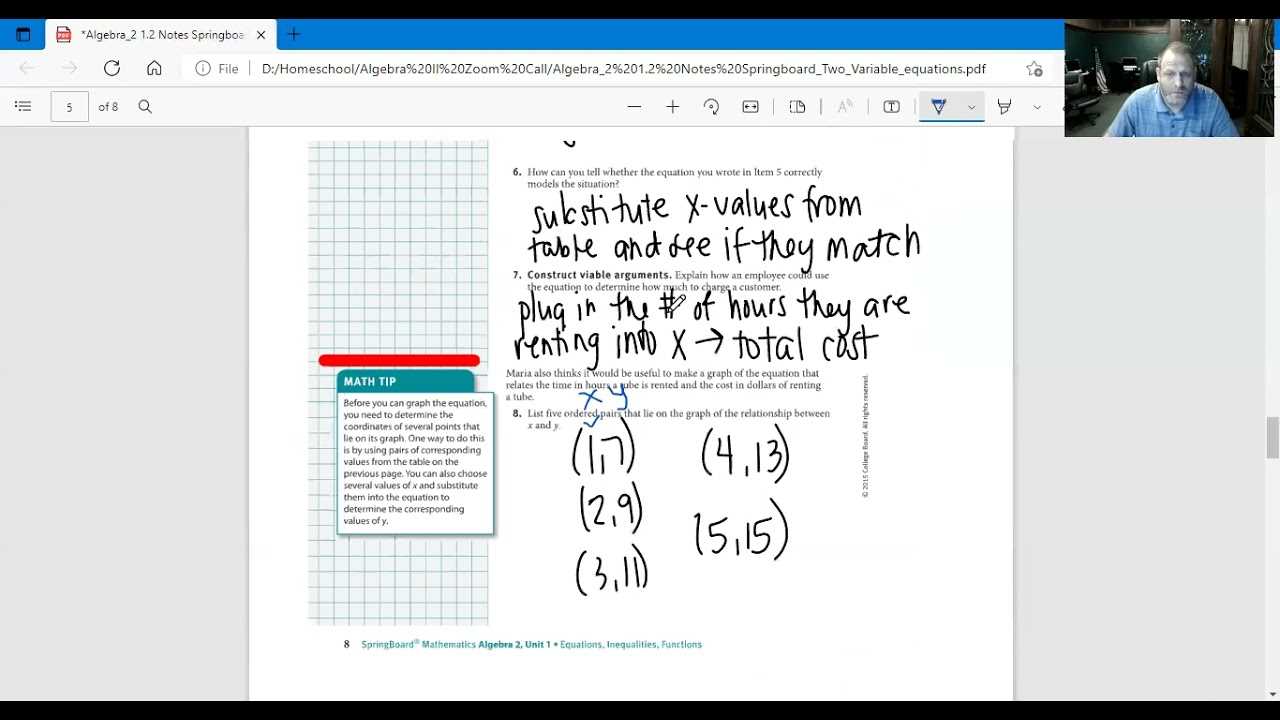
Utilizing the Guide for Success
By consulting this resource, students can identify correct steps and learn how to approach similar problems in the future. Whether tackling linear equations, quadratic functions, or other fundamental topics, the solutions offered allow for a better understanding of how to apply various mathematical principles. Effective use of this guide can enhance retention and improve performance on assignments and tests.
Understanding the Solution Process
The solutions provided are not merely answers but come with detailed explanations and logical steps. Each response is accompanied by a clear outline of how to approach the problem, ensuring that students are not just memorizing results but also learning the process. Mastering these techniques is essential for building confidence and competence in mathematics.
Understanding Algebra 1 Curriculum
The curriculum of an introductory mathematics course is designed to establish a strong foundation in key mathematical concepts. It focuses on various principles that are essential for solving problems, developing critical thinking skills, and preparing for more advanced topics in mathematics. The material covered progresses logically, building on previous knowledge to create a comprehensive understanding of the subject.
Key Topics Covered in the Curriculum
Throughout the course, students explore a range of concepts that are fundamental to higher-level mathematics. Some of the major topics include:
- Equations and inequalities
- Graphing linear functions and relationships
- Quadratic expressions and solving techniques
- Systems of equations
- Exponents and their properties
Course Structure and Approach
The structure of the curriculum is designed to encourage students to gradually build their skills and understanding. It emphasizes problem-solving and applying mathematical methods to real-world scenarios. The course typically includes a combination of theoretical lessons, practice exercises, and assessments to help students master each concept before moving on to more complex topics.
How to Use the Answer Key Effectively
Using a solution guide effectively goes beyond simply checking your work. It’s about understanding the steps involved and learning from the methods used to reach the correct results. A well-organized resource can help you identify errors, improve your problem-solving techniques, and deepen your understanding of mathematical concepts.
Review Step-by-Step Solutions
Instead of just looking at the final answer, take time to review each step of the solution process. By following the logic and reasoning behind each step, you’ll gain insight into the methods used, which will help you solve similar problems independently in the future. Understanding the process is just as important as getting the right result.
Identify and Learn from Mistakes
If your solution differs from the one in the guide, it’s essential to analyze where the mistake occurred. Identify the exact step where the error was made and revisit that part of the problem. This reflection can reveal gaps in understanding and give you the opportunity to reinforce your knowledge.
Key Concepts in Algebra 1 Explained
Understanding the foundational concepts in mathematics is crucial for mastering more advanced topics. This section focuses on essential principles that students must grasp in order to solve problems and develop a solid understanding of mathematical reasoning. Each topic is fundamental to solving equations, working with functions, and applying various techniques to real-life scenarios.
Essential Concepts for Success
Here are some of the core topics covered in the course:
- Linear Equations: Solving equations with variables on both sides.
- Quadratic Functions: Understanding how to solve for unknowns in quadratic equations.
- Exponents: Mastering the rules of exponents and how they are applied in expressions.
- Systems of Equations: Solving multiple equations simultaneously to find common solutions.
- Inequalities: Working with inequalities and understanding their graphical representations.
Building a Strong Foundation
These core concepts are interlinked, and a strong grasp of each one will make it easier to understand more complex ideas. Mastering the basics is the key to advancing in mathematics, and with practice, students will be able to apply these skills to a wide range of problems.
Solving Linear Equations Step-by-Step
Solving linear equations involves isolating the variable to determine its value. By following a structured approach, you can systematically eliminate terms and simplify the equation until the solution is clear. This process requires careful attention to each step to ensure accuracy in the final result.
Steps for Solving Linear Equations
Here’s a general outline for solving a typical linear equation:
- Identify the equation: Start by writing the equation clearly and identifying the variable.
- Combine like terms: Simplify both sides of the equation by adding or subtracting similar terms.
- Isolate the variable: Use inverse operations (addition, subtraction, multiplication, or division) to move terms away from the variable.
- Solve for the variable: Perform the final operation to find the value of the variable.
- Check the solution: Substitute the value of the variable back into the original equation to verify it satisfies the equation.
Example of a Linear Equation
Consider the equation:
2x + 5 = 15
- First, subtract 5 from both sides: 2x = 10.
- Next, divide both sides by 2: x = 5.
- Finally, check by substituting x = 5 back into the original equation: 2(5) + 5 = 15, which is true.
Mastering Quadratic Equations Solutions
Solving quadratic equations requires a clear understanding of the different methods available to find the unknowns. These equations often involve variables raised to the second power, and the solutions can be determined using techniques such as factoring, completing the square, or applying the quadratic formula. Mastery of these methods is essential for tackling more complex problems in higher-level mathematics.
Methods for Solving Quadratic Equations
There are several ways to solve quadratic equations, each with its own set of advantages depending on the problem’s structure. Below is a comparison of the most common methods:
| Method | When to Use | Steps Involved |
|---|---|---|
| Factoring | When the equation can be factored easily. | 1. Write the equation in standard form. 2. Factor the quadratic expression. 3. Set each factor equal to zero and solve. |
| Completing the Square | When the equation is not easily factorable, but can be rewritten as a perfect square. | 1. Rewrite the equation so that the constant term is on the right. 2. Add the square of half the coefficient of x to both sides. 3. Solve by taking the square root of both sides. |
| Quadratic Formula | When other methods are too complex or impossible. | 1. Write the equation in standard form. 2. Use the formula x = (-b ± √(b² – 4ac)) / 2a. 3. Simplify the expression to find the values of x. |
Each of these methods requires practice to be mastered, but with time and experience, solving quadratic equations becomes a straightforward process.
Tips for Tackling Word Problems
Word problems can often seem intimidating, but with the right approach, they become manageable challenges. These problems require translating real-world situations into mathematical expressions, which can then be solved using familiar techniques. The key to success is breaking the problem down into smaller, more manageable steps and understanding the context behind the numbers.
Step-by-Step Approach
Here are some tips to help you approach word problems with confidence:
- Read Carefully: Carefully read the problem more than once to ensure you fully understand what is being asked.
- Identify Known and Unknown Values: Highlight or write down the given information and the unknowns you need to solve for.
- Translate Words into Math: Convert the key phrases or relationships into mathematical expressions or equations.
- Draw a Diagram: For problems involving geometry or movement, drawing a visual representation can make the situation clearer.
- Check Units and Accuracy: Ensure that you are using the correct units and that the numbers make sense in the context of the problem.
- Review the Solution: Once you have found a solution, review the problem again to make sure your answer is logical and satisfies all conditions.
By following these steps, you can break down even the most complex word problems and find the correct solution with ease.
Common Mistakes to Avoid in Algebra 1
When learning mathematical concepts, it’s easy to make errors that can lead to incorrect results. Identifying and understanding these mistakes is an important step in improving problem-solving skills. By recognizing common pitfalls, students can avoid them and approach problems with more confidence and accuracy.
Common Errors and How to Avoid Them
- Incorrectly Simplifying Expressions: Failing to combine like terms or applying incorrect order of operations can lead to mistakes. Always remember to simplify step by step and follow PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).
- Forgetting to Distribute: When multiplying a term across parentheses, be sure to distribute the term to every part of the expression inside. Neglecting this can result in incomplete equations.
- Sign Mistakes: Adding or subtracting with incorrect signs, especially when dealing with negative numbers, is a common mistake. Carefully check the signs before performing calculations.
- Incorrectly Solving for Variables: When solving equations, make sure to isolate the variable correctly. Missteps like dividing or multiplying by the wrong terms can lead to incorrect solutions.
- Overlooking Units: Always keep track of units, especially when dealing with word problems. Ignoring or mismatching units can lead to meaningless answers.
By staying mindful of these frequent errors, you can approach problems more effectively and avoid unnecessary setbacks in your mathematical journey.
How to Prepare for Algebra 1 Tests
Effective preparation is essential to succeed in any mathematics exam. Understanding the material, practicing key concepts, and managing your time are all crucial elements of test readiness. By focusing on the right strategies, you can boost your confidence and improve your performance on test day.
Study Strategies for Success
- Review Class Notes Regularly: Consistently going over notes helps reinforce concepts and makes it easier to identify areas where you need extra practice.
- Practice Problems: Solving a variety of problems is one of the best ways to test your understanding. Focus on problems that challenge you and review those you find difficult.
- Understand Key Concepts: Make sure you understand the fundamental principles behind the problems, such as solving for variables, simplifying expressions, or working with equations. Don’t just memorize steps–comprehend why they work.
- Use Practice Tests: Take mock exams under timed conditions to simulate the test environment. This helps you get comfortable with the format and improves time management.
Effective Time Management
- Create a Study Schedule: Allocate specific times each day to focus on different topics. Spread out your studying to avoid cramming.
- Break It Down: Break complex topics into smaller sections and focus on mastering each one before moving on to the next.
- Take Breaks: Avoid burnout by taking short breaks during study sessions to refresh your mind and maintain focus.
By consistently following these strategies and preparing well in advance, you can approach your tests with confidence and achieve the results you want.
Reviewing Functions and Their Properties
Understanding the concept of functions is central to mastering mathematical relationships. A function describes how one quantity depends on another, where each input is related to exactly one output. In this section, we will explore the key characteristics that define a function and how to analyze these relationships effectively.
Key Characteristics of Functions
- Domain and Range: The domain represents all possible input values, while the range consists of all possible output values. Identifying the domain and range is crucial in understanding the behavior of a function.
- One-to-One and Many-to-One: In a one-to-one function, each input has a unique output, while in a many-to-one function, multiple inputs can produce the same output.
- Increasing and Decreasing Functions: A function is increasing when the output grows as the input increases, and decreasing when the output decreases as the input increases.
- Even and Odd Functions: Even functions are symmetric about the y-axis, while odd functions are symmetric about the origin. Recognizing this symmetry can help simplify problems.
Analyzing Function Graphs
- Intercepts: The x-intercepts and y-intercepts of a function can provide key insights into its behavior and location on the coordinate plane.
- Asymptotes: Some functions have asymptotes, which are lines that the function approaches but never touches. Understanding vertical, horizontal, and oblique asymptotes is vital for graphing complex functions.
- Slope and Curvature: The slope of a function indicates its steepness, while the curvature describes whether the function is concave up or down. These properties help in sketching accurate graphs.
By understanding these properties, you can more effectively analyze and graph different types of functions, laying a strong foundation for tackling more advanced mathematical topics.
Exploring Inequalities and Solutions
Understanding inequalities is an essential part of solving real-world mathematical problems. Unlike equations, inequalities describe relationships where one quantity is not necessarily equal to another but may be greater or smaller. The goal is to find the range of values that satisfy these relationships, which is crucial for analyzing situations involving constraints, such as budgets, measurements, or comparisons.
Types of Inequalities
- Linear Inequalities: These involve variables raised to the first power and express relationships like “greater than” or “less than.” The solution is typically a range of values.
- Quadratic Inequalities: These inequalities involve squared variables and can produce solutions that are ranges or intervals on the number line.
- Absolute Value Inequalities: These involve expressions with absolute values and represent situations where the distance of a number from zero is within a certain range.
Graphing Solutions
Visualizing the solutions to inequalities is often done on a number line or coordinate plane. The key is to understand how to represent the range of possible values and whether the endpoints are included or excluded from the solution.
| Inequality | Graph Representation | Solution Description |
|---|---|---|
| x ≥ 2 | Closed circle at 2, shaded to the right | The solution includes 2 and all numbers greater than 2. |
| x | Open circle at 4, shaded to the left | The solution includes all numbers less than 4 but not 4 itself. |
| |x| | Shaded region between -3 and 3 | The solution includes all numbers whose distance from zero is less than 3. |
By understanding the different types of inequalities and how to represent their solutions, you can better approach problems that involve restrictions or comparisons between values.
Graphing Linear Equations and Functions
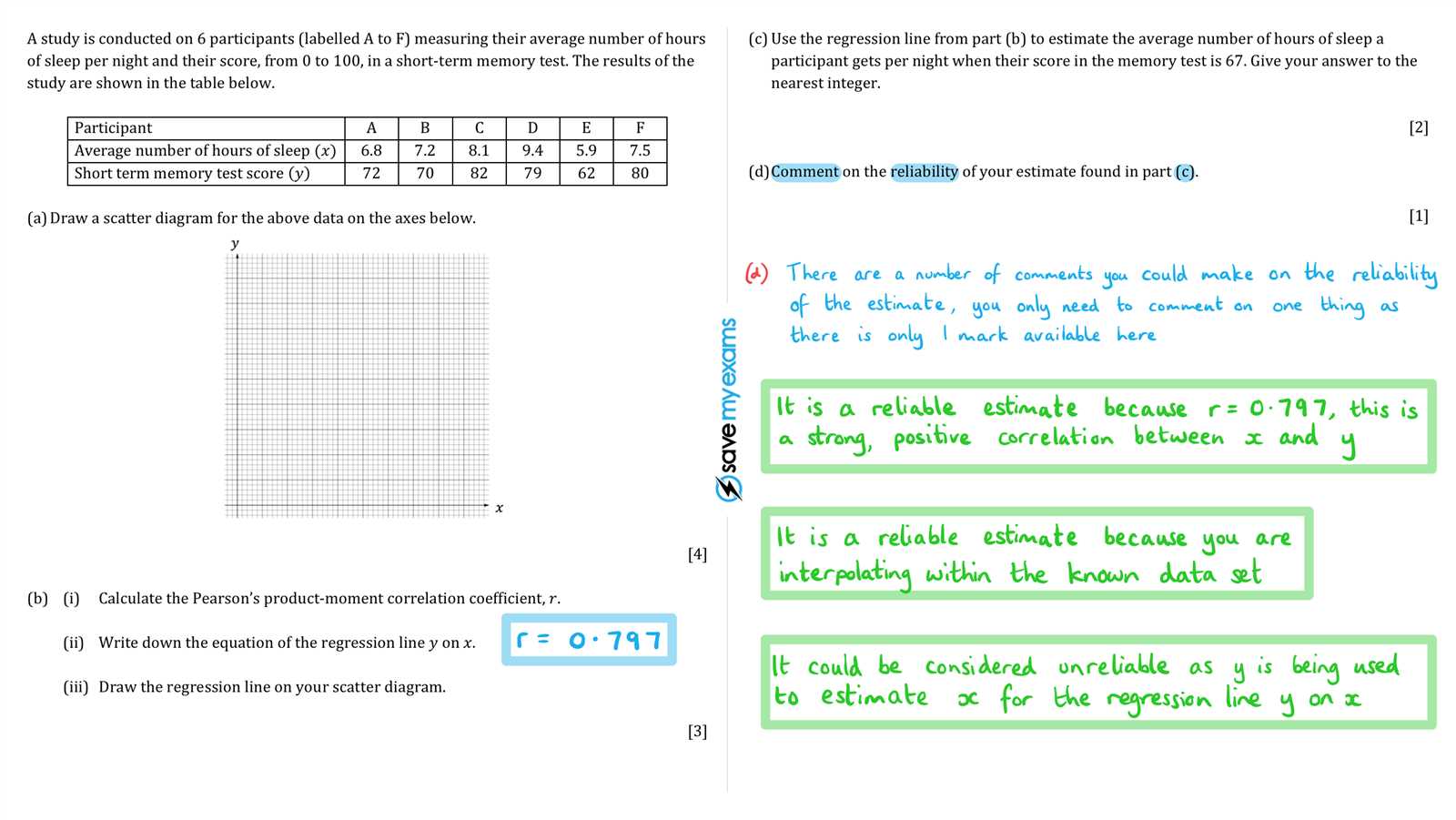
Graphing linear equations and functions is a fundamental skill in mathematics. It allows us to visually represent relationships between variables, helping to better understand patterns and solutions. In this section, we will explore how to graph lines and analyze their properties based on different forms of equations.
Understanding the Slope-Intercept Form
One of the most common forms for representing linear relationships is the slope-intercept form. The general equation is written as:
y = mx + b
- m: The slope of the line, indicating its steepness. It is calculated as the change in y divided by the change in x (rise over run).
- b: The y-intercept, which is the point where the line crosses the y-axis. This represents the value of y when x equals zero.
Steps to Graph a Line
- Find the y-intercept: Start by plotting the y-intercept (b) on the graph.
- Use the slope: From the y-intercept, use the slope (m) to find another point on the line. For example, if the slope is 2/3, rise 2 units and run 3 units to the right.
- Draw the line: Connect the two points and extend the line in both directions, making sure it is straight.
By following these steps, you can graph any linear equation that is given in slope-intercept form. The process helps visualize the relationship between the variables and provides insight into how the values change in relation to each other.
Graphing with Other Forms

While the slope-intercept form is popular, linear equations can also be written in other forms, such as the point-slope form or standard form. Each of these forms offers a different approach for graphing, but the underlying principle remains the same: to represent a straight line on a coordinate plane.
Understanding Polynomials and Factoring

Polynomials are expressions that involve sums and differences of terms, where each term consists of a variable raised to a power and multiplied by a constant. The ability to simplify and manipulate polynomials is a crucial skill in mathematics. One important technique for simplifying polynomials is factoring, which helps break down complex expressions into simpler, more manageable parts.
What Are Polynomials?
A polynomial is an expression made up of variables, coefficients, and exponents, combined using addition, subtraction, and multiplication. Polynomials can have one or more terms and may involve different degrees, which correspond to the highest exponent of the variable in the expression. For example:
- Linear Polynomial: 2x + 3
- Quadratic Polynomial: x² + 5x + 6
- Cubic Polynomial: x³ – 2x² + 3x – 4
Each type of polynomial follows its own set of rules for solving, graphing, and factoring.
Factoring Polynomials
Factoring involves finding the components or factors that, when multiplied together, give the original polynomial. This technique is valuable because it simplifies expressions and makes solving equations easier. Common methods of factoring include:
- Greatest Common Factor (GCF): The first step in factoring is often to find the greatest common factor of the terms in the polynomial and factor it out.
- Factoring Trinomials: This involves breaking a quadratic polynomial into two binomials, often using trial and error or the ac-method.
- Difference of Squares: This special case applies when the polynomial is a difference between two perfect squares, such as x² – 9, which factors to (x + 3)(x – 3).
Mastering factoring techniques enables you to solve polynomial equations and simplify expressions, making them much easier to work with in higher-level mathematics.
Exponents and Exponential Functions Guide
Exponents and exponential functions are essential concepts in mathematics that help simplify complex expressions and model real-world phenomena. An exponent indicates how many times a number, known as the base, is multiplied by itself. Exponential functions, on the other hand, involve variables in the exponent, which can model growth and decay in a wide range of disciplines, from finance to biology.
Understanding Exponents
An exponent refers to the number that tells you how many times the base number is used as a factor. For example, in the expression 34, 3 is the base and 4 is the exponent, meaning 3 is multiplied by itself four times (3 × 3 × 3 × 3). Here are some key rules to remember:
- Product of Powers: When multiplying two expressions with the same base, add the exponents: am × an = am+n.
- Power of a Power: When raising a power to another power, multiply the exponents: (am)n = am×n.
- Zero Exponent: Any nonzero number raised to the power of zero equals one: a0 = 1.
- Negative Exponent: A negative exponent indicates the reciprocal of the base raised to the positive exponent: a-n = 1/an.
Exploring Exponential Functions
An exponential function is a type of function where the variable appears in the exponent. The general form is f(x) = a × bx, where “a” is a constant, “b” is the base, and “x” is the exponent. These functions are used to describe processes that grow or decay at a constant rate, such as population growth, compound interest, or radioactive decay.
- Exponential Growth: When the base “b” is greater than 1, the function represents growth, with values increasing rapidly as “x” increases.
- Exponential Decay: When the base “b” is between 0 and 1, the function represents decay, with values decreasing over time.
Exponential functions have important properties, such as a horizontal asymptote and rapid growth or decay. Understanding these functions allows for modeling and solving real-world problems involving rates of change.
Fraction Operations in Algebra 1
Working with fractions is a crucial skill in mathematics that extends into many areas of study. Understanding how to manipulate fractions–whether through addition, subtraction, multiplication, or division–lays the foundation for solving more complex problems. Fractions can represent parts of a whole and appear in various forms across equations and expressions. Mastering fraction operations is essential for simplifying expressions and solving equations effectively.
Adding and Subtracting Fractions
Adding and subtracting fractions requires finding a common denominator. This ensures that the fractions are in a comparable form and allows for straightforward addition or subtraction. The steps for adding or subtracting fractions are:
- Find the least common denominator (LCD) of the fractions.
- Rewrite each fraction with the LCD as the denominator.
- Add or subtract the numerators, keeping the denominator the same.
- Simplify the fraction if possible.
Multiplying and Dividing Fractions
Multiplying and dividing fractions is simpler than adding or subtracting, as these operations do not require a common denominator. Here’s how to perform them:
- Multiplying: Multiply the numerators and denominators separately. For example, (a/b) × (c/d) = (a × c) / (b × d).
- Dividing: To divide fractions, multiply the first fraction by the reciprocal of the second. For example, (a/b) ÷ (c/d) = (a/b) × (d/c).
Example of Fraction Operations
Below is a table showing an example of each operation with fractions:
| Operation | Example | Result |
|---|---|---|
| Addition | 1/4 + 2/4 | 3/4 |
| Subtraction | 3/5 – 1/5 | 2/5 |
| Multiplication | 2/3 × 3/4 | 6/12 (or 1/2) |
| Division | 4/7 ÷ 2/5 | 4/7 × 5/2 = 20/14 (or 10/7) |
By understanding and practicing these basic operations, you can confidently handle fractions in more advanced problems, simplifying expressions and solving equations with ease.
Helpful Resources for Algebra 1 Students
Success in mathematics requires access to the right tools and materials. A variety of resources can support students in mastering fundamental concepts and improving their problem-solving skills. These resources range from online platforms and interactive tools to textbooks and practice exercises, providing different approaches to learning. With the right support, students can deepen their understanding and approach each topic with confidence.
Online Learning Platforms
Online resources can be a game-changer, offering flexibility and interactive experiences for students. Some popular platforms for reinforcing key topics include:
- Khan Academy: Offers comprehensive lessons and practice exercises on a wide range of topics, from basic operations to complex equations.
- IXL: A personalized learning platform with skills-based practice, progress tracking, and real-time feedback to help students improve.
- Desmos: An interactive graphing calculator and learning tool that helps students visualize mathematical concepts and solve problems efficiently.
Textbooks and Reference Materials
Books remain a valuable resource for students looking for in-depth explanations and structured problem sets. Some recommended textbooks and guides include:
- Pre-Algebra and Algebra 1 Workbooks: These workbooks offer a variety of practice questions and step-by-step solutions to reinforce learning.
- Schaum’s Outline Series: Known for its clear explanations and large number of practice problems, perfect for exam preparation.
- College Board’s SAT Prep Book: This resource is useful for students looking to prepare for standardized tests while reinforcing mathematical concepts.
By utilizing these resources, students can enhance their understanding of mathematical principles, build their problem-solving skills, and achieve success in their coursework.
How to Check Your Answers Accurately
Verifying the correctness of your solutions is an essential step in problem-solving. By carefully reviewing your work, you can identify mistakes, ensure precision, and reinforce your understanding of the process. There are several effective methods to confirm that your solutions are accurate, from retracing your steps to utilizing alternative techniques for validation.
One of the most important approaches is to substitute your results back into the original equation or problem. This allows you to see if the solution satisfies the given conditions. Additionally, it’s useful to break down complex problems into smaller, more manageable parts, checking each step as you go. By doing so, you can spot errors early in the process and avoid carrying them through to the final solution.
Another strategy is to use different methods to solve the same problem. For example, if you’re working with equations, try solving them using both algebraic manipulations and graphical methods. Comparing the results from different approaches can provide greater confidence in the correctness of your solution.
Finally, practice plays a crucial role in enhancing accuracy. As you gain more experience with various types of problems, your ability to spot errors and verify answers will improve over time, leading to greater confidence in your work.
Improving Your Mathematical Skills Over Time
Mastering mathematical concepts takes time, practice, and dedication. Whether you’re just beginning or seeking to enhance your existing skills, consistent effort can lead to significant improvement. There are various strategies that can help you build a strong foundation and progressively advance in your understanding of mathematical principles.
Here are some practical tips for improving your skills:
- Practice Regularly: The more you engage with problems, the better you will become at identifying patterns and applying techniques. Daily practice helps solidify your knowledge and boosts your problem-solving abilities.
- Focus on Conceptual Understanding: Rather than memorizing formulas or procedures, strive to understand the reasoning behind them. Grasping the “why” behind the steps you take will make it easier to apply these concepts to various problems.
- Break Down Complex Problems: When faced with challenging problems, break them into smaller, more manageable parts. Solving each part step by step can make the overall task seem less daunting and more approachable.
- Review and Reflect: After solving a problem, go back and review your work. Reflect on the methods you used, check for mistakes, and consider alternative solutions. This helps reinforce learning and prevents the repetition of errors.
- Seek Help When Needed: Don’t hesitate to ask for assistance if you encounter difficult concepts. Discussing problems with teachers, peers, or using online resources can provide fresh perspectives and new strategies.
Incorporating these habits into your routine will help you gradually build confidence and competence in mathematics. Over time, your skills will improve, allowing you to tackle more advanced topics with ease.