Geometry Practice Test Answers and Detailed Solutions

Success in solving mathematical problems requires a deep understanding of core principles and the ability to apply them to various situations. With consistent practice, students can sharpen their skills and gain confidence in their ability to tackle complex questions. This section aims to provide a comprehensive guide to help you improve problem-solving techniques and deepen your knowledge of key concepts.

Through clear, step-by-step solutions and expert tips, you will be able to navigate through challenging exercises and identify common pitfalls. Understanding the logic behind each solution will not only enhance your problem-solving abilities but also help you approach each task with a strategic mindset.

Effective preparation is crucial for achieving mastery. By reviewing different types of exercises and focusing on areas of difficulty, you can progressively build your skills. Embracing various strategies will enable you to perform efficiently and accurately in any given scenario.

Mathematical Problem Solutions Explained

Mastering problem-solving in mathematics requires more than just knowing formulas. It involves understanding the logic and reasoning behind each solution, allowing you to apply techniques to a wide range of scenarios. In this section, we break down common exercises to provide clear explanations, making complex concepts more approachable and easier to grasp.

Breaking Down Each Step

Each problem requires a series of logical steps to arrive at the correct result. By analyzing each stage of the process, we can pinpoint key concepts and techniques that lead to a solution. Understanding these individual steps helps reinforce the core principles, ensuring that similar problems can be solved efficiently in the future.

Common Pitfalls and How to Avoid Them

Even the most experienced learners can fall into traps while solving mathematical problems. Misinterpreting a question or overlooking important details can lead to errors. By identifying these common mistakes and learning how to avoid them, you can approach each challenge with greater confidence and accuracy.

Understanding Key Mathematical Concepts

To excel in solving complex problems, it is essential to grasp the fundamental ideas that underpin each exercise. A solid understanding of the core principles not only helps in deriving the correct solutions but also enables you to approach new challenges with clarity and confidence. In this section, we explore the critical concepts that form the foundation of problem-solving strategies.

Each principle serves as a building block, helping to connect seemingly unrelated topics and offering insights into more advanced techniques. By focusing on the underlying theories and their practical applications, you can develop a more intuitive understanding of how to approach problems and find effective solutions.

How to Approach Mathematical Problems

When facing any challenging problem, a structured approach can make all the difference. Knowing how to break down a question, analyze the information provided, and select the best strategy is key to finding the correct solution. In this section, we’ll explore a step-by-step method for tackling questions effectively and efficiently.

Step 1: Understand the Problem

Before jumping into solving a problem, it’s crucial to fully understand what’s being asked. Take a moment to read through the problem carefully and identify the key elements. Ask yourself:

• What is the problem asking for?
• What information is given?
• Are there any conditions or restrictions to consider?

Identifying these details early on will help you avoid confusion as you work through the problem.

Step 2: Plan Your Approach

Once you have a clear understanding, it’s time to plan how to approach the solution. Consider the following strategies:

1. Look for patterns or relationships between the elements.
2. Decide which formulas or concepts might apply.
3. Break the problem into smaller, manageable parts.
4. Consider visual aids, such as diagrams, if applicable.

Having a strategy in place will ensure that your approach is logical and efficient, reducing the chances of errors along the way.

Common Mistakes in Mathematical Assessments

Even experienced individuals can make errors when solving complex problems. Often, these mistakes are not due to a lack of knowledge but rather result from oversights or misunderstandings during the problem-solving process. Identifying common pitfalls can help prevent them and improve accuracy in future exercises.

Some of the most frequent mistakes include misinterpreting the question, neglecting to apply the correct formula, or overlooking important details in the problem statement. These errors can lead to incorrect solutions, even when the approach appears sound at first glance.

Another common issue is rushing through the calculations without double-checking steps or final results. Taking the time to carefully review each part of the process can prevent small mistakes from having a big impact on the overall outcome.

Step-by-Step Solutions for Mathematical Problems

Approaching a problem with a clear, structured method can lead to a correct and efficient solution. Breaking down the problem into smaller, manageable steps ensures that nothing is overlooked and makes it easier to spot any errors. In this section, we provide a detailed guide on how to work through complex exercises step by step.

Step 1: Identify Key Information

The first step in solving any problem is to extract all the relevant data from the question. This means identifying known values, variables, and relationships that will guide your solution. You can organize this information in a table for clarity.

Given Information	Required Solution
Side lengths of a triangle	Find the area
Angles of a polygon	Calculate the sum of the interior angles

Step 2: Apply the Correct Method

Once the necessary details are identified, it’s time to apply the appropriate methods or formulas to solve the problem. Ensure that you are using the correct approach based on the given information. If applicable, draw diagrams or visualize the situation to help you better understand the relationships at play.

Mastering Mathematical Theorems and Postulates

To solve complex mathematical problems, a deep understanding of the fundamental principles and logical rules is essential. Theorems and postulates form the backbone of many solutions, providing a framework for proving relationships between different elements. Mastering these concepts is key to building a strong foundation for more advanced problem-solving.

Theorems are statements that have been proven based on earlier established principles, while postulates are accepted as true without the need for proof. Understanding how to apply these ideas effectively allows you to navigate a wide variety of challenges and derive conclusions based on solid reasoning.

By familiarizing yourself with the most important theorems and postulates, and regularly practicing their application, you can significantly enhance your problem-solving skills and approach each question with confidence.

Tips for Effective Mathematical Assessment Preparation

Preparing for any type of assessment requires focus, organization, and strategic planning. To perform at your best, it’s essential to develop a clear study plan, practice consistently, and understand the core concepts that will be tested. In this section, we provide practical tips to help you get ready and improve your performance.

Start by reviewing key concepts and focusing on areas where you feel least confident. Make a list of essential formulas and theorems, and spend time understanding their applications. The more familiar you become with these building blocks, the quicker you’ll be able to solve problems during the actual assessment.

Practice regularly with a variety of problems to build confidence and speed. Work through both simple and complex examples to reinforce your skills. Simulate testing conditions by timing yourself and avoiding distractions during practice sessions. This will help you manage time effectively on the day of the assessment.

Improving Speed and Accuracy in Mathematical Problem Solving

In mathematics, being both quick and precise is crucial for success. While solving problems efficiently, it’s important to avoid rushing through steps that could lead to mistakes. Striking the right balance between speed and accuracy comes with practice and the development of effective strategies. In this section, we discuss how to enhance both aspects for better performance.

Time Management Strategies

To improve speed, it’s essential to practice time management during exercises. Set specific time limits for each problem to simulate real assessment conditions. Focusing on speed will help you learn to identify shortcuts and more efficient methods to reach a solution.

• Break down each problem into smaller, manageable steps.
• Focus on using memorized formulas and techniques to avoid wasting time.
• Prioritize problems you find easier to solve first, then tackle the harder ones.

Maintaining Accuracy While Speeding Up

While it’s tempting to rush through problems, maintaining accuracy is just as important as improving speed. Rechecking your work after completing a solution can catch small errors and ensure that you’ve used the right methods. Over time, as you become more familiar with the concepts, accuracy will naturally improve as well.

• Double-check your calculations before finalizing your answer.
• Review the question to make sure you’ve interpreted it correctly.
• Keep practicing to improve both your speed and the precision of your solutions.

Mathematical Word Problems Solved

Word problems can be some of the most challenging types of exercises, as they require not only an understanding of mathematical concepts but also the ability to translate real-world scenarios into solvable equations. In this section, we explore how to approach and solve these types of problems by breaking them down into clear steps.

The key to solving word problems is identifying the relevant information, forming the correct equation, and applying the appropriate methods. By following a structured approach, you can simplify complex problems and reach the correct solution more efficiently.

Problem	Approach	Solution
A car travels 60 miles in 1 hour. How far will it travel in 3 hours?	Use the formula: Distance = Speed × Time	Distance = 60 × 3 = 180 miles
The area of a rectangle is 48 square units. If the length is 8 units, what is the width?	Use the formula: Area = Length × Width	Width = 48 ÷ 8 = 6 units

Using Diagrams to Solve Mathematical Problems

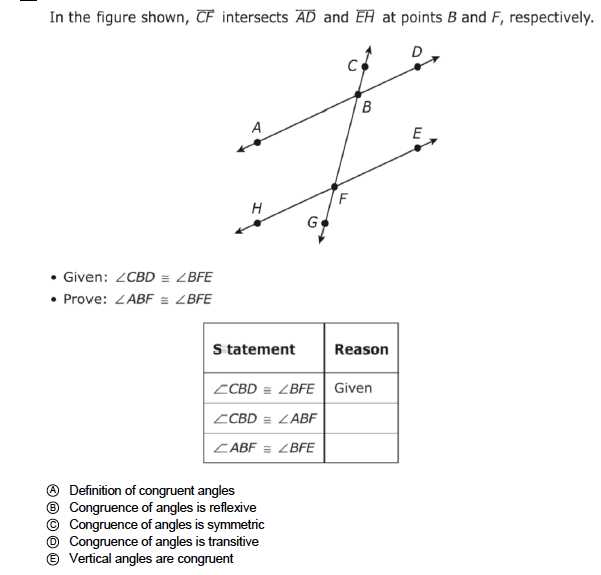
Visual aids, such as diagrams, are powerful tools when solving complex problems. By converting abstract concepts into clear, tangible images, diagrams allow you to better understand relationships and find solutions more efficiently. In this section, we discuss how diagrams can be used to simplify problem-solving and clarify key ideas.

When faced with a problem, drawing a diagram can help you organize the given information and visualize the connections between different elements. This step is especially useful for problems involving shapes, angles, or spatial reasoning. Understanding the problem visually can often provide insights that may not be immediately obvious through words alone.

Whether it’s labeling sides of a figure or marking key angles, diagrams can guide you through the logical steps of a solution. The more practice you get with visualizing problems, the easier it becomes to see patterns and determine the correct approach.

Mathematical Proofs and Logical Reasoning

In mathematics, proving statements requires a systematic application of logical reasoning. Proofs are used to demonstrate the truth of a given assertion, and they rely on established principles, facts, and step-by-step logical deductions. This section focuses on how to approach and construct proofs by following a clear logical framework.

When working through a proof, it’s essential to use a structured approach, starting with known facts and working towards the conclusion. Logical reasoning helps ensure that each step is valid and leads to a sound conclusion. Below are some key elements to keep in mind when constructing proofs:

• Clearly define known information: Start by listing all given facts and assumptions.
• Use logical steps: Apply known theorems, properties, and postulates to move towards the conclusion.
• Ensure every step follows logically: Make sure each statement follows from the previous one.
• Draw conclusions from evidence: Conclude only after all necessary steps have been taken and all conditions have been met.

By practicing logical reasoning and developing the ability to build coherent arguments, you’ll gain confidence in tackling more complex proofs and enhance your overall problem-solving skills.

Assessment Preparation Strategies for Mathematical Problem Solving

Effective preparation for any assessment involves more than just reviewing concepts. To perform well under exam conditions, it’s crucial to develop specific strategies that allow you to approach problems efficiently and minimize mistakes. This section explores key techniques to improve your readiness and maximize your performance when facing complex exercises.

Time Management Techniques

One of the most important strategies for any assessment is managing your time wisely. It’s essential to allocate sufficient time for each question while also allowing some moments to revisit any challenging problems. Time management ensures that you can complete the entire assessment without rushing at the end, and also gives you time to review your work for potential errors.

• Set a fixed time limit for each problem based on its complexity.
• Skip over questions that are too time-consuming and return to them later.
• Practice solving problems within a time frame to build speed without sacrificing quality.

Strategic Problem-Solving Approaches

Not all problems should be approached in the same way. Analyzing the structure of the question and identifying patterns can lead to quicker solutions. Start with easier questions to build momentum and leave more complex problems for later, once you’ve warmed up. Focus on applying the most efficient methods to solve each question while keeping an eye on accuracy.

• Read each problem carefully to understand exactly what’s being asked.
• Use diagrams or visual aids whenever possible to simplify the problem.
• Break down complex questions into smaller, manageable parts.

Calculating Angles and Distances in Mathematical Problems

In mathematical problem-solving, determining angles and distances is a fundamental skill that is often required to solve complex scenarios. These calculations are essential for understanding the relationships between different elements in a figure and help in deriving accurate solutions. In this section, we will explore how to effectively calculate angles and distances and apply these techniques in various exercises.

Finding Angles in Various Figures

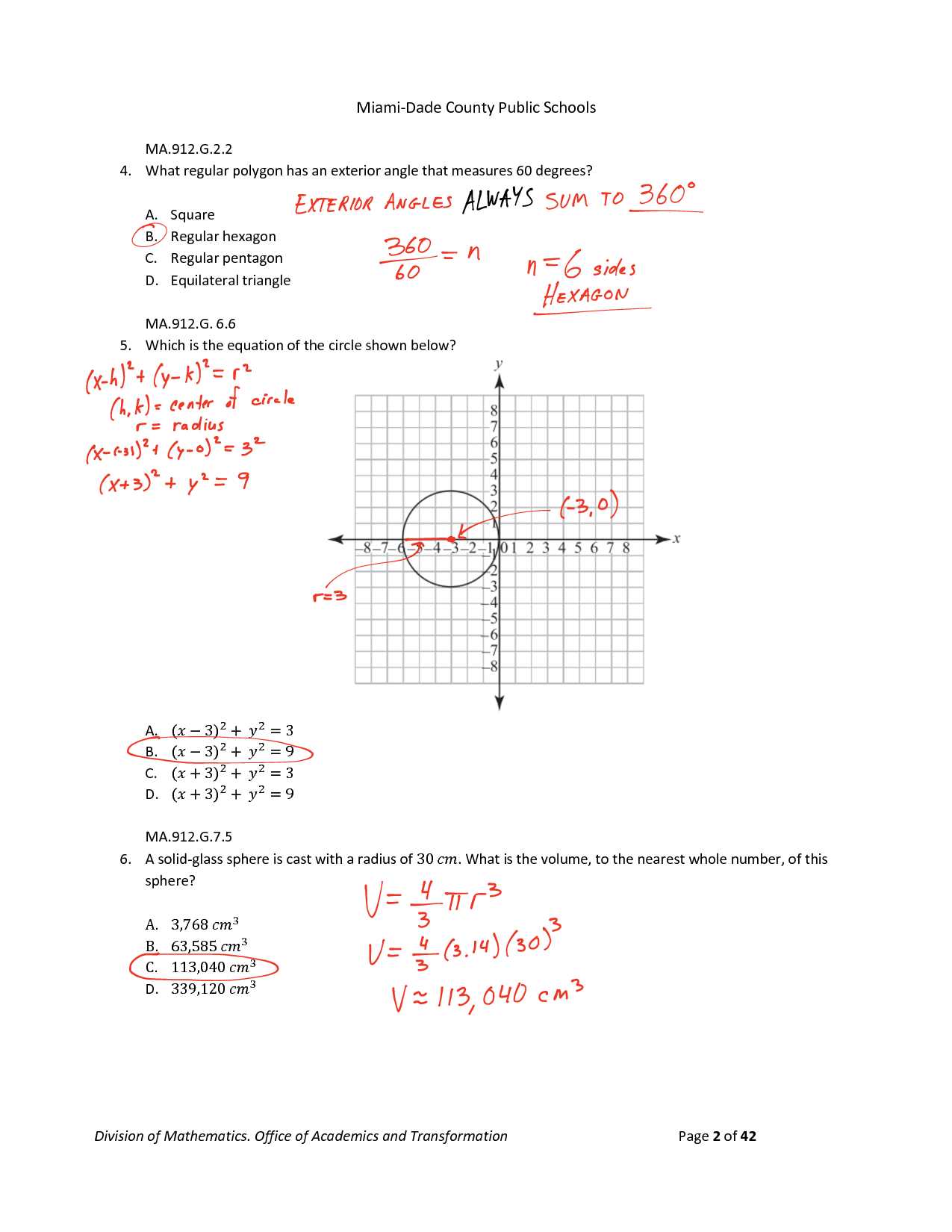
Angles are key components in many problems, and calculating them accurately is crucial. Different types of angles, such as complementary, supplementary, and vertical angles, follow specific rules that can simplify the process. By understanding the relationships between angles in a given figure, you can solve for unknowns and develop a clearer understanding of the problem.

• Complementary Angles: Two angles that add up to 90°.
• Supplementary Angles: Two angles that add up to 180°.
• Vertical Angles: Angles formed by two intersecting lines, always equal to each other.

Measuring Distances Using Formulas

Accurate distance calculations are equally important in solving problems involving figures. Distances between points can be calculated using various methods, such as the distance formula in a coordinate plane. Whether you’re working with straight lines or curves, using the correct formula is essential for obtaining precise results.

• Distance Formula: For two points (x₁, y₁) and (x₂, y₂), the distance is calculated as √[(x₂ – x₁)² + (y₂ – y₁)²].
• Pythagorean Theorem: Used to find the length of a side in a right triangle, a² + b² = c².

Solving for Area and Volume in Mathematical Problems

Understanding how to calculate the area and volume of various shapes is essential for solving a wide range of mathematical problems. These calculations allow you to determine the size of two-dimensional surfaces and the capacity of three-dimensional objects. In this section, we will explore the formulas and methods used to calculate area and volume for different figures, and how these concepts are applied in problem-solving.

Calculating Area of Two-Dimensional Shapes

To solve for the area of a shape, it’s important to use the correct formula based on the type of figure involved. The area represents the amount of space enclosed within a boundary. Each shape has its own specific formula, and understanding how to apply these is key to solving related problems.

• Square: Area = side²
• Rectangle: Area = length × width
• Circle: Area = π × radius²
• Triangle: Area = ½ × base × height

Determining Volume of Three-Dimensional Objects

Volume is a measure of the space occupied by a three-dimensional object. To solve for volume, you must use the appropriate formula for the shape in question. The volume calculation can often be more complex than area but follows the same principle of multiplying measurements of the object’s dimensions.

• Cube: Volume = side³
• Rectangular Prism: Volume = length × width × height
• Cylinder: Volume = π × radius² × height
• Sphere: Volume = (4/3) × π × radius³

Essential Formulas You Must Remember

Mastering key formulas is crucial for solving a wide variety of mathematical problems. These formulas serve as the foundation for determining properties of different shapes, from basic areas to complex volume calculations. Knowing these formulas by heart can save you time and help you approach problems with confidence. Below are some of the most important formulas that you should remember for successful problem-solving.

Important Area Formulas

Calculating the area of two-dimensional figures is fundamental in many exercises. The area represents the amount of space enclosed within the boundaries of a figure, and each shape has a unique formula for finding it.

• Square: Area = side²
• Rectangle: Area = length × width
• Triangle: Area = ½ × base × height
• Circle: Area = π × radius²

Essential Volume Formulas

For three-dimensional figures, volume determines the amount of space the object occupies. Understanding how to calculate volume is necessary for solving problems related to solids.

• Cube: Volume = side³
• Rectangular Prism: Volume = length × width × height
• Cylinder: Volume = π × radius² × height
• Sphere: Volume = (4/3) × π × radius³

How to Review Practice Assessments

Reviewing completed assessments is an essential part of the learning process, as it allows you to identify mistakes and areas for improvement. Instead of simply checking your results, it’s important to reflect on the reasoning behind each question and understand where errors may have occurred. This process helps reinforce concepts and prepares you for similar challenges in the future. Here’s how to approach the review of these exercises effectively.

Step-by-Step Review Process

Follow these steps to thoroughly review your completed assessments and ensure you learn from every mistake:

1. Start with the questions you got wrong: Focus on understanding why your answers were incorrect. Did you misinterpret the question, make a calculation error, or forget a crucial concept?
2. Check the solution method: Compare your solution to the correct approach. Were there any steps you skipped or misunderstood?
3. Understand the correct reasoning: Break down the correct steps and ensure you grasp the logic behind the solution.

Key Strategies for Effective Review

Using effective strategies will help you make the most out of your review session:

• Practice similar problems: After reviewing, practice with similar questions to strengthen your understanding and test your ability to apply concepts.
• Write down key takeaways: Note the concepts or techniques that you struggled with so that you can revisit them later.
• Seek help when necessary: If a particular problem or concept is still unclear, don’t hesitate to ask for assistance from a tutor or peer.

Advanced Techniques for Test Success

Mastering advanced strategies can significantly improve your performance when tackling complex problems. These techniques go beyond basic formulas and help you develop a deeper understanding of the relationships between different shapes, angles, and measurements. By incorporating these methods into your preparation, you can enhance your ability to approach and solve challenging problems with confidence.

Key Advanced Strategies

To increase your chances of success, apply the following strategies to enhance your problem-solving abilities:

Technique	Description
Coordinate Geometry	Use the coordinate plane to calculate distances, midpoints, and slopes. This method is particularly useful for analyzing geometric figures that are represented algebraically.
Transformation Geometry	Understand how shapes can be moved, rotated, or reflected. This helps in identifying symmetries and simplifying complex figures for easier calculation.
Trigonometry	Apply trigonometric ratios such as sine, cosine, and tangent to solve for unknown sides or angles in right-angled triangles. This technique is vital for working with non-rectangular shapes.
Proof Techniques	Develop strong logical reasoning skills to prove geometric relationships. Mastering indirect and direct proof methods will help you justify your solutions clearly and concisely.

Additional Tips for Advanced Problem Solving

Along with advanced strategies, these additional tips can further optimize your approach:

• Visualize the problem: Drawing diagrams and labeling key elements can help you better understand the relationships between various components.
• Break down complex problems: Divide large problems into smaller, more manageable parts to simplify the process and reduce the chance of mistakes.
• Double-check your work: Revisit the steps you’ve taken to ensure there are no errors in your calculations or reasoning.