Core Connections Algebra Chapter 9 Answers

In this section, we delve into the fundamental concepts and techniques essential for tackling complex mathematical challenges. Whether you’re working with equations, inequalities, or functions, a clear understanding of the methods presented will help you navigate through a variety of problems efficiently. This guide is designed to provide clarity and practical solutions to enhance your problem-solving skills.
Mastering the essential methods is crucial for developing a deeper understanding of mathematics. With the right strategies, even the most intricate problems can be simplified. By breaking down concepts step by step, you can build a solid foundation that will not only help you solve similar problems but also prepare you for more advanced topics in the future.
Throughout this material, you’ll encounter a range of exercises and explanations, each crafted to reinforce your learning. The goal is not only to provide correct solutions but also to highlight the thought process behind each step. This approach ensures that you grasp the logic behind mathematical procedures, empowering you to apply these skills in various real-world situations.
Mathematical Problem Solutions for Chapter 9
This section focuses on providing solutions and insights to the problems found in the ninth unit of the course. It covers a variety of essential techniques and methodologies for solving different types of exercises. Whether you’re facing challenges with equations, expressions, or real-world applications, this guide is designed to give you a thorough understanding of the necessary steps to find accurate solutions.
To assist in mastering these concepts, we present the solutions in a clear and structured manner. Each step is explained logically, allowing you to follow the process easily and gain a deeper understanding of the underlying principles. This approach not only helps you solve the current set of problems but also prepares you for future challenges.
- Understanding the basics: Begin with the foundational concepts that underpin the mathematical operations and procedures used in the problems.
- Breaking down complex problems: Learn how to simplify complicated scenarios into manageable steps, ensuring clarity throughout the solving process.
- Applying techniques to different scenarios: Use the strategies learned to tackle various types of problems with confidence, whether linear equations, inequalities, or functions.
By reviewing each problem and its corresponding solution, you will develop a clearer perspective on how to approach similar exercises in the future. Consistent practice and understanding the logic behind each step are key to mastering these mathematical techniques.
Understanding Key Mathematical Concepts
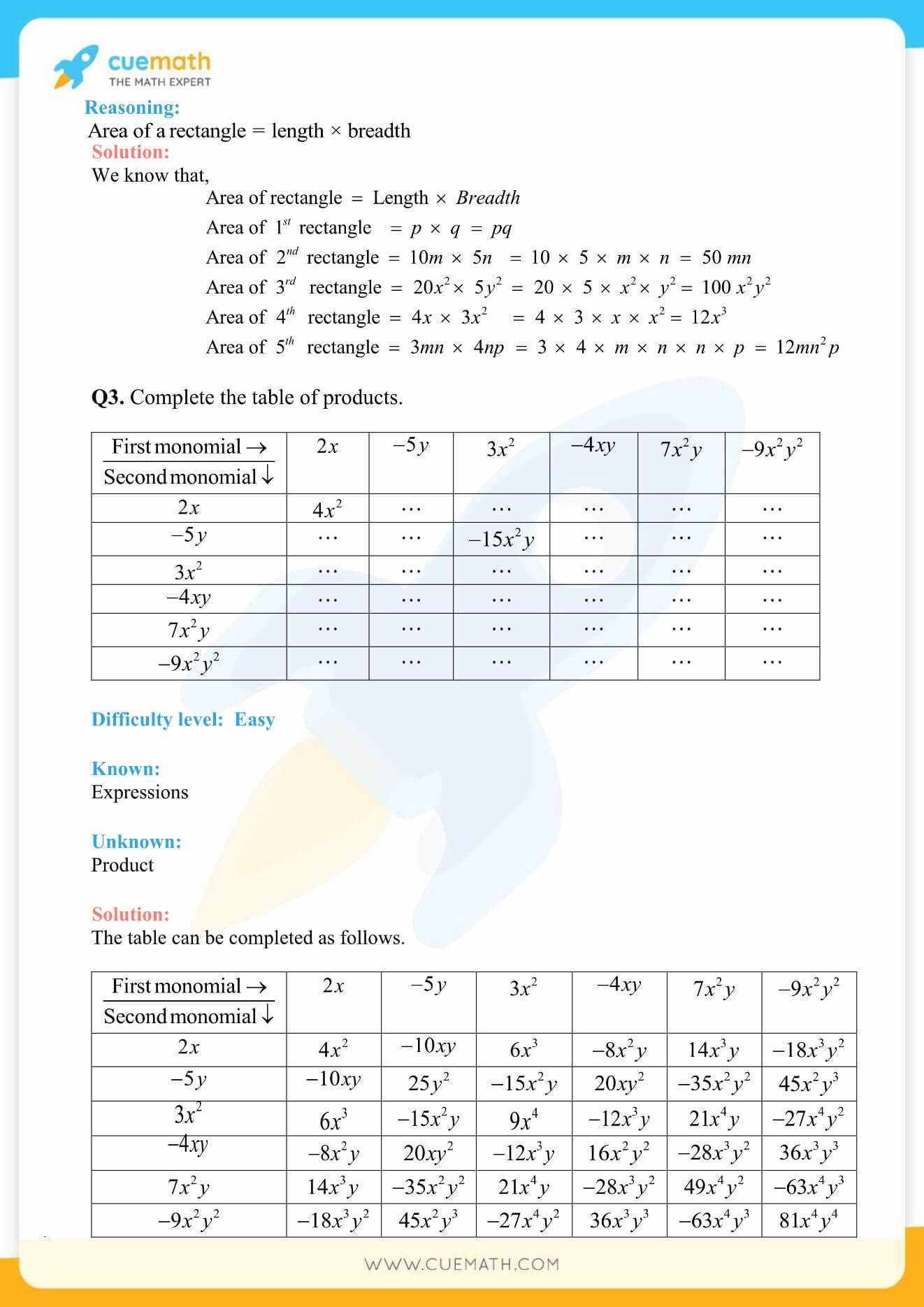
Grasping the essential principles of mathematics is crucial for solving a variety of problems effectively. At the heart of most exercises lies a set of fundamental rules that guide the solving process. By mastering these core ideas, you’ll be able to approach complex equations and scenarios with greater confidence and accuracy.
Throughout this section, the focus is on the fundamental techniques that form the basis for more advanced topics. From working with variables to solving for unknowns, understanding how these core concepts interrelate will provide a solid foundation for tackling a wide range of mathematical challenges.
Once you have a firm grasp on these basic ideas, you’ll be better equipped to navigate more complex situations. The key is not just memorizing formulas, but understanding the logic behind each step and knowing how to apply them in various contexts.
Step-by-Step Solution Guide
In this section, we will walk you through the process of solving mathematical problems by breaking down each step into manageable parts. The goal is to provide clarity and ensure that you understand the logic behind every action taken to reach the solution. By following this methodical approach, you will be able to tackle a wide variety of problems with confidence.
Breaking Down the Problem
The first step in solving any problem is understanding its structure. Start by identifying the given information and the desired outcome. Carefully read through the problem to recognize what you are being asked to find. This will help you determine which methods or operations are necessary for solving it.
Applying Mathematical Operations
Once the problem is broken down, proceed by applying the appropriate mathematical operations. Whether it’s simplifying expressions, solving for variables, or finding solutions to equations, each operation should be performed systematically. Take your time with each step to ensure accuracy and prevent mistakes.
By following this step-by-step approach, you’ll develop a clearer understanding of how to solve similar problems in the future. Practice and consistency are key to mastering any mathematical concept.
Common Mistakes to Avoid
While solving mathematical problems, it’s easy to make errors that can lead to incorrect results. Recognizing and avoiding these common mistakes is essential for improving accuracy and developing stronger problem-solving skills. By being mindful of these pitfalls, you can significantly reduce the likelihood of making these errors and enhance your overall understanding of the material.
Rushing Through Steps
One of the most frequent mistakes is moving too quickly through the process. Skipping steps or failing to double-check calculations can lead to overlooked errors. It’s important to work through each stage carefully, ensuring that every operation is completed properly. Take your time to check each solution before moving on to the next part of the problem.
Misinterpreting the Problem

Another common issue arises from misreading or misinterpreting the problem. Ensure you fully understand what is being asked before you begin solving. Pay attention to details such as negative signs, fractions, or specific instructions, as these can significantly impact the approach you need to take. Clarifying the question will help you avoid unnecessary confusion during the solving process.
By being aware of these typical mistakes and taking steps to avoid them, you can improve your problem-solving accuracy and increase your overall performance.
Strategies for Mathematical Problem Solving
When tackling mathematical challenges, having a set of effective strategies can make a significant difference in your ability to find solutions. These techniques help organize your thinking, simplify complex problems, and ensure that each step is completed correctly. By applying the right methods, you can approach any problem with confidence and accuracy.
- Understand the Problem: Start by carefully reading the question. Identify the known values and what you are trying to find. A clear understanding of the problem is essential to determine which methods to apply.
- Break Down Complex Problems: If a problem seems overwhelming, break it into smaller, manageable parts. Solve each part step by step, then combine the results for the final solution.
- Use Logical Operations: Apply basic mathematical operations systematically. Whether simplifying expressions, isolating variables, or working through equations, maintaining logical consistency is key to achieving accurate results.
- Check Your Work: After completing a solution, always revisit each step. Verifying your calculations ensures that no mistakes have been made, helping you arrive at the correct final answer.
By following these strategies, you will improve your ability to solve problems more efficiently, building a solid foundation for both simple and complex mathematical tasks.
Tips for Mastering Mathematical Concepts
Mastering key mathematical principles requires dedication and the right approach. By focusing on essential strategies and techniques, you can build a strong understanding of the material, making it easier to solve problems and apply concepts effectively. These tips will help you improve your skills and deepen your grasp of the subject.
- Practice Regularly: Consistent practice is crucial for reinforcing your understanding. The more you practice, the more comfortable you will become with different problem types and mathematical methods.
- Focus on Conceptual Understanding: Rather than just memorizing formulas or steps, aim to understand the logic behind each process. This deeper comprehension will make it easier to apply techniques in new situations.
- Work on Example Problems: Review solved examples and work through them step by step. This helps you see how different techniques are applied and provides insight into the problem-solving process.
- Seek Help When Needed: Don’t hesitate to ask for assistance if you’re struggling with certain concepts. Whether through a tutor, classmate, or online resources, getting help can clarify complex ideas and prevent confusion.
By integrating these tips into your study routine, you’ll gradually build the skills needed to excel in mathematics. With time and persistence, mastering these concepts will become a more attainable goal.
How to Approach Word Problems
Word problems can seem daunting at first, but with the right approach, they can be tackled efficiently. The key is to break down the information, identify what is being asked, and apply the appropriate mathematical methods step by step. By following a structured approach, you’ll be able to turn complex word problems into manageable tasks.
Here is a general strategy for solving word problems:
| Step | Description |
|---|---|
| Read the Problem Carefully | Understand the scenario presented. Identify the key details, such as quantities, relationships, and what is being asked for. |
| Identify Variables | Assign symbols to unknown values. This helps in translating the word problem into a mathematical equation. |
| Set Up the Equation | Based on the information given, create an equation or system of equations that represents the problem. |
| Solve the Equation | Use appropriate mathematical operations to solve the equation for the unknown variable(s). |
| Check the Solution | Verify that the solution makes sense in the context of the problem and satisfies all conditions. |
By following these steps, you can break down any word problem into smaller, more manageable parts, making it easier to solve and ensuring that you arrive at the correct answer.
Exploring Algebraic Expressions
Mathematical expressions are fundamental building blocks for solving a wide range of problems. These expressions combine numbers, variables, and mathematical operations to represent relationships or quantities. By learning how to work with these expressions, you gain the ability to simplify, evaluate, and manipulate them to solve various types of problems effectively.
Understanding Variables and Constants
In any expression, you will encounter variables and constants. Variables are symbols that stand for unknown values, while constants are fixed numbers. Understanding the role of each component helps in interpreting the meaning behind an expression. For example, in the expression 3x + 5, “x” is the variable, while “3” and “5” are constants that help determine the value of the expression when the variable is known.
Operations Within Expressions

Mathematical operations such as addition, subtraction, multiplication, and division are the fundamental processes used within expressions. These operations determine how the values and variables are combined. It’s essential to follow the correct order of operations (often remembered by the acronym PEMDAS) to ensure that expressions are simplified correctly and accurately.
By gaining a deeper understanding of algebraic expressions, you’ll be better equipped to handle more complex problems and solve them step by step. This foundational knowledge is critical for success in a wide range of mathematical topics.
Practice Exercises for Chapter 9

Practicing mathematical problems is essential for reinforcing the concepts you’ve learned and improving your problem-solving skills. By working through various exercises, you can test your understanding, identify areas that need further review, and build confidence in applying the techniques to new problems. These exercises are designed to challenge your knowledge and help you master the material.
- Exercise 1: Simplify the expression 5x + 3y – 2x + 7y.
- Exercise 2: Solve the equation 3(2x – 4) = 18 for x.
- Exercise 3: Expand the expression (x + 5)(x – 3).
- Exercise 4: Factor the quadratic expression x² + 7x + 12.
- Exercise 5: Solve the system of equations:
- x + y = 10
- 2x – y = 4
These practice problems will help solidify your understanding and prepare you for more complex topics. Be sure to take your time with each exercise, checking your work as you go along to ensure accuracy.
Key Formulas to Remember
Formulas are essential tools for solving a wide variety of mathematical problems. Memorizing key formulas allows you to quickly apply them when needed, making problem-solving faster and more efficient. Below are some of the fundamental formulas that are often used in mathematical tasks. Understanding and remembering these will help you tackle problems with greater ease.
Basic Arithmetic and Operations
- Distributive Property: a(b + c) = ab + ac – This property allows you to distribute a multiplier across a sum or difference.
- Commutative Property of Addition: a + b = b + a – The order of addition does not affect the result.
- Commutative Property of Multiplication: ab = ba – The order of multiplication does not affect the result.
- Associative Property: (a + b) + c = a + (b + c) – Grouping does not affect the result for addition or multiplication.
Quadratic Equations and Factoring

- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a – Use this formula to solve any quadratic equation of the form ax² + bx + c = 0.
- Factoring of a Quadratic Expression: ax² + bx + c = (px + q)(rx + s) – This is the process of finding two binomials whose product gives the quadratic expression.
- Difference of Squares: a² – b² = (a – b)(a + b) – This formula is used to factor the difference between two squares.
By familiarizing yourself with these formulas, you’ll have a solid foundation for solving a wide range of problems. Be sure to review and practice them regularly to enhance your problem-solving skills.
Algebraic Techniques for Success
Mastering mathematical methods is key to solving complex problems efficiently. By applying systematic approaches and utilizing various strategies, you can simplify difficult tasks and gain clarity in solving equations, expressions, and systems. Whether you’re tackling linear equations, quadratic expressions, or systems of equations, using the right techniques will significantly improve your problem-solving abilities.
Effective Strategies for Simplifying Equations
- Isolate the Variable: Focus on getting the variable alone on one side of the equation. This simplifies the process and helps identify the solution more clearly.
- Combine Like Terms: Group terms that have the same variable or constant to make the equation simpler and more manageable.
- Use Substitution: For systems of equations, substitute one equation into another to eliminate one variable, making it easier to solve for the remaining variable.
Advanced Techniques for Solving Complex Problems
- Factoring: Factoring expressions, such as quadratics, helps simplify them into products of binomials, which are easier to solve.
- Quadratic Formula: For more complex quadratic equations, the quadratic formula is a reliable tool to find the solutions when factoring is difficult.
- Graphing: Plotting equations on a graph can give a visual representation of their solutions, making it easier to identify intersections and understand the behavior of the function.
By consistently practicing these techniques, you’ll not only improve your mathematical skills but also develop a deeper understanding of problem-solving strategies. Keep refining these methods to tackle even more challenging problems with confidence.
Understanding Linear Equations

Linear equations are fundamental in mathematics, as they represent relationships between variables in a straight-line format. These equations describe how one quantity changes with respect to another, and they are typically expressed in the form of a constant rate of change. Understanding how to manipulate and solve these equations is crucial for solving more complex mathematical problems.
A linear equation typically involves two variables, with the highest exponent of the variables being one. This makes the graph of the equation a straight line when plotted on a coordinate plane. The main goal when solving a linear equation is to find the value of the unknown variable, usually represented by x or y.
For example, the equation 3x + 5 = 11 is a simple linear equation. To solve for x, one must isolate the variable by performing inverse operations:
- Subtract 5 from both sides: 3x = 6
- Divide both sides by 3: x = 2
By following these steps, you can solve any linear equation and determine the value of the unknown variable. Mastery of linear equations is essential for tackling more advanced topics such as systems of equations, inequalities, and graphing linear functions.
Solving Inequalities with Ease
Solving inequalities is a critical skill that allows you to understand relationships where one quantity is greater than, less than, or not equal to another. Unlike equations, inequalities do not have a single solution but instead represent a range of possible values. By learning the proper techniques, solving these can be just as straightforward as solving equations.
Key Techniques for Solving Inequalities
When solving inequalities, the goal is to isolate the variable just like in equations. However, there is one important distinction: when multiplying or dividing both sides of an inequality by a negative number, you must reverse the inequality sign. Keeping this rule in mind ensures accuracy in finding the solution set.
- Addition or Subtraction: You can add or subtract the same number from both sides of the inequality without changing the inequality’s direction.
- Multiplication or Division: Be cautious when multiplying or dividing by negative numbers, as this will flip the inequality sign.
Example of Solving an Inequality
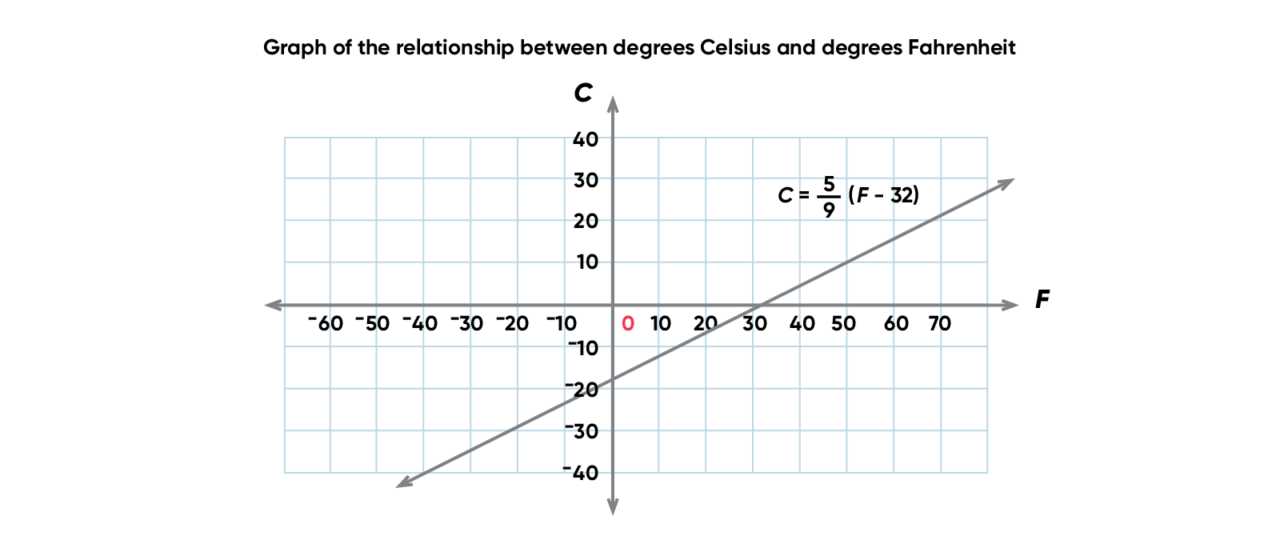
Consider the inequality -2x + 5 > 11. To solve for x, follow these steps:
- Subtract 5 from both sides: -2x > 6
- Divide both sides by -2 (and reverse the inequality): x
Thus, the solution to the inequality is x , meaning any value less than -3 satisfies the inequality.
By practicing these steps, you’ll be able to solve inequalities quickly and efficiently, gaining a deeper understanding of their applications in real-world problems.
Graphing Algebraic Functions
Graphing mathematical functions is an essential skill for visualizing relationships between variables. By plotting a function on a coordinate plane, you can better understand how different values of one variable affect another. This process is useful not only for simple equations but also for more complex relationships, helping to uncover patterns and trends.
To graph a function, it is important to first identify key elements such as the domain, range, and any intercepts. These features provide valuable information about the shape and behavior of the graph. Once these components are understood, plotting points and drawing the function’s curve becomes a systematic process.
Steps for Graphing a Basic Function
Here’s a general approach for graphing basic functions:
- Identify the function: Determine the type of function you are working with (linear, quadratic, etc.) and the variables involved.
- Find key points: Start by calculating a few points that satisfy the function. For example, choose values for x and solve for y to generate ordered pairs.
- Plot the points: Once you have a set of points, plot them on the coordinate grid.
- Draw the graph: Connect the points, considering the function’s general behavior (e.g., straight line, curve).
For example, consider the function y = 2x + 3. To graph this, choose values for x, such as -2, 0, and 2, and solve for y. This will give you the points (-2, -1), (0, 3), and (2, 7). Plotting these points on the coordinate plane and drawing a straight line through them will yield the graph of the function.
Example Table for Plotting
| x | y = 2x + 3 |
|---|---|
| -2 | -1 |
| 0 | 3 |
| 2 | 7 |
By following these steps and using the table to organize data, you can graph a wide variety of functions and gain a deeper understanding of their behavior.
Using Real-World Applications
Mathematical concepts extend beyond the classroom and can be applied to everyday situations, providing solutions to real-world problems. By understanding the principles of mathematical equations, individuals can make informed decisions in a variety of fields, such as finance, engineering, and even daily life tasks. Applying these skills in practical scenarios helps to see the true value of abstract concepts and strengthens problem-solving abilities.
Whether calculating expenses, determining travel time, or optimizing resources, math allows us to model and solve many problems effectively. The key is to identify the relevant variables and construct the correct equations or models to represent the situation.
Examples of Real-World Problems
- Budgeting and Finance: By using simple equations, one can calculate income, expenses, and savings. For example, setting up an equation to determine how much money remains after monthly expenses.
- Speed and Distance: When planning a trip, it’s essential to calculate travel time based on speed and distance. Using the relationship between these variables can help predict arrival times accurately.
- Construction and Design: Engineers and architects use mathematical formulas to design buildings, calculate areas, or estimate the amount of materials needed for a project.
Practical Example: Budgeting for a Trip
Imagine you’re planning a weekend getaway. You have a budget and need to figure out how much you can spend on travel, accommodation, and activities. The equation might look like:
Total Budget = Travel Cost + Accommodation Cost + Activity Cost
If your total budget is $500, the travel cost is $150, and you plan to spend $100 on accommodation, the remaining budget for activities can be calculated as:
Remaining Budget = $500 – ($150 + $100) = $250
This simple calculation helps ensure that you stay within your budget, allowing for a more enjoyable and stress-free trip.
Reviewing Key Concepts and Techniques
Revisiting important ideas and methods from earlier lessons is crucial for reinforcing understanding and ensuring mastery of the material. This section focuses on the main strategies and skills that have been introduced, providing a comprehensive review to help solidify foundational knowledge. Whether you’re preparing for an assessment or simply looking to enhance your grasp of the subject, reviewing key concepts can significantly boost confidence and problem-solving abilities.
Throughout this review, we will revisit various problem-solving techniques, simplify complex topics, and highlight the most important formulas and methods used. By revisiting these areas, you will be able to approach similar problems with greater ease and precision.
Key Methods and Strategies
- Understanding Variables and Expressions: It’s essential to identify variables and understand how they relate to each other in an equation. This allows for the proper manipulation and simplification of expressions.
- Solving Equations: Mastering the techniques for isolating variables and solving for unknowns is a fundamental skill that applies to a wide range of problems. This includes both linear and non-linear equations.
- Graphing Functions: A visual representation of mathematical relationships can provide additional insight. Understanding how to graph equations, identify key points, and interpret slopes is vital for deeper comprehension.
Common Challenges and Solutions
Some common difficulties students face include managing multiple variables, recognizing patterns, and accurately solving for unknowns. However, these challenges can often be overcome by practicing basic techniques, breaking down problems into smaller steps, and double-checking work to ensure accuracy.
By practicing regularly and reviewing key strategies, you can develop stronger problem-solving skills and achieve greater success in tackling complex problems.
Preparing for Assessments in Mathematical Concepts
Effective preparation is essential for excelling in assessments that evaluate mathematical understanding and problem-solving abilities. To achieve the best possible results, it is important to approach your preparation with a structured plan. This section highlights key steps and strategies for preparing for tests focused on various mathematical topics, from equations and functions to graphing and transformations.
Successful test preparation involves not only reviewing material but also practicing different types of problems, familiarizing yourself with the test format, and developing strong time-management skills. Below are some of the most effective approaches to prepare thoroughly for any assessment.
Key Steps for Effective Preparation
- Review Key Concepts: Go over the main concepts, focusing on the topics that you find most challenging. Reinforce your understanding of essential principles and make sure you understand the logic behind each method.
- Practice Problem Solving: Regularly solving practice problems is crucial. This will help you become familiar with the types of questions likely to appear and improve your problem-solving speed and accuracy.
- Understand Common Mistakes: Identify common pitfalls in solving mathematical problems. By learning from your mistakes, you can avoid them on test day and improve your overall performance.
- Review Past Tests: If available, review any previous tests or practice assessments. This allows you to understand the test structure and gain insight into which types of problems are frequently tested.
- Ask for Help: Don’t hesitate to ask for assistance from a tutor or peers if you’re struggling with a particular concept. Collaboration and discussion often lead to deeper understanding.
Time Management Strategies for Test Day
On the day of the test, managing your time efficiently is essential. Below are some tips to help you stay on track:
| Strategy | Description |
|---|---|
| Prioritize Easy Questions | Start with the questions you find easiest to build confidence and secure quick points. |
| Time Allocation | Divide your time evenly among all sections, ensuring you have time to answer every question. |
| Review Your Work | Leave time at the end to go over your answers and double-check for errors or missed questions. |
By following these steps and strategies, you will be well-equipped to tackle any mathematical assessment with confidence and precision.