Solving Equations with Variables on Both Sides Answers
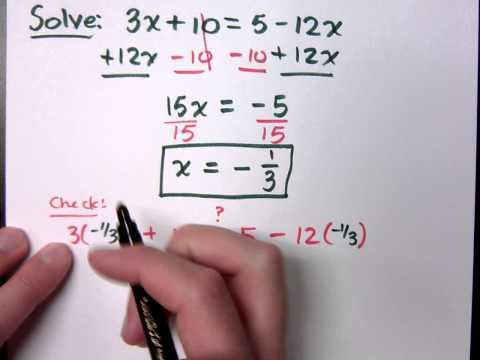
In mathematics, the process of working through problems that involve unknown quantities on different parts of an expression is an essential skill. It requires a clear understanding of how to manipulate terms and simplify expressions until the unknowns are isolated. This ability is fundamental not only in academic studies but also in real-world problem solving, from budgeting to engineering designs.
The key to mastering these problems lies in understanding the principles of balancing both ends of the expression. Whether adding, subtracting, multiplying, or dividing, each operation brings us closer to a solution. The goal is to work systematically and avoid common pitfalls, ensuring the result is both accurate and meaningful.
By following a structured approach and applying various techniques, such as combining like terms or using inverse operations, anyone can learn to handle such challenges with confidence. This guide will walk you through the steps needed to solve these types of problems effectively, providing clear explanations and practical examples.
Solving Equations with Variables on Both Sides Answers
When working on problems involving unknown quantities positioned in different parts of a mathematical expression, the goal is to isolate the unknown while maintaining balance. This task requires a series of logical steps, where each operation plays a crucial role in simplifying the expression until the solution is clear. Here are the steps to follow when handling such problems:
- Step 1: Simplify each part of the expression by combining like terms and removing any unnecessary parentheses.
- Step 2: Move the unknowns to one side by using addition or subtraction, ensuring both sides remain balanced.
- Step 3: Perform operations such as multiplication or division to isolate the unknown quantity.
- Step 4: Verify the solution by substituting the value of the unknown back into the original expression to check for consistency.
For better understanding, consider the following example:
- Expression: 3x + 5 = 2x + 9
- Step 1: Subtract 2x from both sides: x + 5 = 9
- Step 2: Subtract 5 from both sides: x = 4
In this example, the solution is x = 4. By applying these steps, you can confidently approach problems of this nature and ensure your solutions are correct. With practice, these methods will become second nature, allowing for faster and more accurate results in similar situations.
Understanding the Basics of Equations
At the heart of algebra lies the concept of balancing mathematical expressions. The objective is to find the unknowns, which are typically represented by letters, by performing operations that maintain equality. Each operation applied to one part of the expression must also be applied to the other side to keep both parts equivalent. The idea is simple: whatever you do to one side of an expression, you must do to the other to preserve the relationship between the two parts.
Key Components of an Expression
An expression consists of constants, unknowns, and operations that link them. The unknowns are the values you aim to determine, while constants are fixed numbers. Operations like addition, subtraction, multiplication, and division are the tools used to manipulate these elements to reveal the unknowns.
| Term Type | Example |
|---|---|
| Constant | 5, -3, 8 |
| Unknown | x, y, z |
| Operation | +, -, ×, ÷ |
The Concept of Balance
Think of a mathematical expression as a scale, where both sides must be equal for the statement to hold true. If you adjust one side by adding or subtracting a number, the same change must be made to the other side. This balance is crucial for finding the value of the unknowns accurately.
Grasping these foundational principles is essential for progressing to more complex tasks. As you begin to manipulate expressions, maintaining equality through each step becomes your primary focus, allowing you to uncover the unknowns with precision.
Identifying Variables in an Expression
In many mathematical problems, there are unknown quantities that we need to determine. These unknowns are represented by symbols, typically letters, within the expression. Recognizing these symbols is the first step in solving such problems. By identifying the unknowns, you can focus on the necessary steps to find their values and work toward a solution.
The unknowns are usually the parts of the expression that change based on the conditions of the problem. In some cases, there may be more than one unknown, and it becomes important to track them accurately to avoid confusion. These symbols often appear alongside constants, which are fixed numbers.
For example, in an expression like 3x + 5 = 14, the symbol x is the unknown, which we are trying to determine. The constants in this case are the numbers 3, 5, and 14. Recognizing this distinction helps simplify the process of isolating the unknown and finding its value.
When looking at more complex expressions, you may encounter several unknowns. In such cases, it’s important to carefully identify each one and keep track of them as you manipulate the expression to solve for their values.
Step-by-Step Approach to Solving
When tackling mathematical problems involving unknowns, following a clear, logical sequence of steps is crucial for finding the solution. Breaking the task into manageable parts allows you to handle each operation systematically while ensuring the integrity of the expression. This approach helps in simplifying the process and avoiding common mistakes.
General Steps to Follow
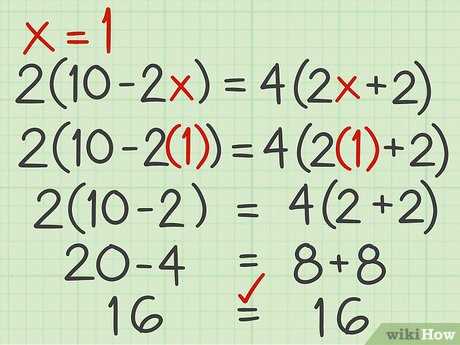
Here’s a step-by-step guide to approaching problems where unknowns are present on both ends of an expression:
- Step 1: Simplify each part of the expression by combining like terms and removing unnecessary parentheses.
- Step 2: Move all the terms containing unknowns to one side by using addition or subtraction. This will help in isolating the unknown.
- Step 3: Perform operations like multiplication or division to simplify further and isolate the unknown value.
- Step 4: Check the solution by substituting the value of the unknown back into the original expression to ensure both sides are balanced.
Example Problem
Consider the following problem:
- Expression: 4x + 7 = 3x + 10
- Step 1: Subtract 3x from both sides: 4x – 3x + 7 = 10
- Step 2: Combine like terms: x + 7 = 10
- Step 3: Subtract 7 from both sides: x = 3
By following this structured approach, you can solve similar problems with confidence and accuracy. Each step builds on the previous one, bringing you closer to isolating the unknown and finding the correct value.
Isolating Variables on One Side

One of the key steps in working with mathematical expressions involving unknowns is to isolate the unknown on one part of the expression. This makes it easier to solve for the unknown and determine its value. The process involves moving all terms related to the unknown to one side, while keeping constants on the other side, using operations that maintain balance in the expression.
Steps for Isolating the Unknown
Here is a general method to isolate the unknown in a given expression:
- Step 1: Eliminate any terms involving the unknown on the side where they do not belong by adding or subtracting.
- Step 2: Once the unknown is on one side, eliminate any constants by performing inverse operations such as adding or subtracting them.
- Step 3: If necessary, simplify the remaining expression by multiplying or dividing both sides by the same factor to isolate the unknown completely.
Example Problem
For instance, consider the expression:
- Expression: 5x + 8 = 3x + 12
- Step 1: Subtract 3x from both parts: 5x – 3x + 8 = 12
- Step 2: Combine like terms: 2x + 8 = 12
- Step 3: Subtract 8 from both parts: 2x = 4
- Step 4: Divide by 2: x = 2
In this example, we successfully isolated the unknown x on one side, and through systematic steps, determined its value to be 2. This approach ensures clarity and accuracy when handling more complex expressions involving unknowns.
Combining Like Terms Effectively
When simplifying expressions, one of the most important steps is combining like terms. This process involves grouping together terms that have the same type of components, such as constants or terms involving the same unknown. By combining these terms, you can reduce the complexity of the expression and make it easier to solve or manipulate.
Efficiently combining like terms is essential for simplifying an expression and preparing it for further steps. It reduces the number of terms, making the problem more manageable and straightforward to solve.
Understanding Like Terms

Like terms are terms that share the same variable raised to the same power. The coefficients of these terms can differ, but the variable part must be identical. For example, 3x and 5x are like terms, while 3x and 5y are not.
| Term Type | Example | Can Be Combined? |
|---|---|---|
| Constant | 7, -4, 9 | Yes |
| Linear Term | 5x, -2x, 3x | Yes |
| Different Variable Terms | 3x, 4y, -x | No |
How to Combine Like Terms
To combine like terms, follow these steps:
- Step 1: Identify terms that contain the same variables and powers.
- Step 2: Add or subtract the coefficients of those terms.
- Step 3: Rewrite the expression with the simplified terms.
For example, in the expression 4x + 7 + 3x – 5, we combine the like terms 4x and 3x, resulting in 7x. The constants 7 and -5 combine to give 2. The simplified expression is 7x + 2.
By mastering the process of combining like terms, you can effectively simplify expressions and move closer to finding the solution to the problem at hand.
Using Addition and Subtraction in Solving
In many mathematical problems, addition and subtraction are the foundational operations used to simplify and manipulate expressions. These operations help in isolating unknowns by moving terms from one part of the expression to another while maintaining the balance of the entire system. Understanding when and how to apply these operations is crucial for progressing toward a solution.
Using Addition to Simplify Expressions
One of the primary ways to simplify an expression is by using addition. When an unknown is being added to a constant, you can remove that constant by subtracting it from both parts of the expression. This keeps the equation balanced and allows you to isolate the unknown more easily.
- Example: In x + 5 = 10, subtract 5 from both parts to isolate x: x = 5
- Example: In 3x + 8 = 14, subtract 8 from both parts to simplify: 3x = 6
Using Subtraction to Move Terms
Subtraction is equally important when dealing with expressions involving unknowns. It allows you to remove terms from one part of the equation, effectively simplifying it and bringing you closer to isolating the unknown. By subtracting appropriate terms from both parts, you ensure the equation remains balanced and the unknown is isolated on one side.
- Example: In x – 7 = 5, add 7 to both parts to solve for x: x = 12
- Example: In 2x – 4 = 6, add 4 to both parts to simplify: 2x = 10
Both addition and subtraction are essential tools in simplifying and isolating terms in an expression. Mastering these operations is critical for solving problems that involve unknowns, as they help manipulate and simplify the expression into a manageable form.
Multiplying and Dividing Both Sides
When working with expressions that contain unknowns, multiplication and division are powerful tools for manipulating and simplifying the equation. These operations help balance both parts of an expression, allowing us to isolate the unknown and make it easier to find its value. By multiplying or dividing both parts by the same number, we maintain the equality of the expression while getting closer to the solution.
Using Multiplication to Simplify
Multiplying both parts of an expression by the same number can help eliminate fractions or scale terms to make the expression simpler. This step is especially useful when dealing with fractions or coefficients that need to be adjusted to isolate the unknown.
- Example: In 1/2 x = 4, multiply both parts by 2 to eliminate the fraction: x = 8
- Example: In 3/4 x = 6, multiply both parts by 4 to clear the fraction: 3x = 24
Using Division to Simplify
Division is often used to isolate the unknown when it is multiplied by a coefficient. By dividing both parts of the expression by the same number, we can simplify the equation and isolate the unknown.
- Example: In 5x = 20, divide both parts by 5 to find x = 4
- Example: In 4x = 24, divide both parts by 4 to find x = 6
Multiplying and dividing are essential techniques for manipulating expressions and simplifying problems involving unknowns. By applying these operations correctly, we can move through the problem-solving process more efficiently and effectively isolate the unknown to find its value.
Checking Solutions for Accuracy
Once you have found a potential solution, it is crucial to verify its correctness. This step ensures that the value you have found satisfies the original problem and that no mistakes were made during the process. Checking the solution is an essential part of problem-solving, as it confirms the validity of your work and guarantees that your answer is accurate.
Steps to Verify the Solution
To confirm that a solution is correct, follow these steps:
- Step 1: Substitute the found value back into the original expression.
- Step 2: Perform the necessary calculations to check if both parts of the expression are equal.
- Step 3: If both sides are equal, the solution is correct; if not, revisit the problem-solving steps.
Examples of Checking Solutions
Let’s look at a couple of examples to illustrate how to check solutions:
- Example 1: If the solution is x = 3 for the expression 2x + 4 = 10, substitute 3 for x:
- 2(3) + 4 = 6 + 4 = 10, which is correct.
- Example 2: If the solution is x = 5 for the expression 3x – 2 = 13, substitute 5 for x:
- 3(5) – 2 = 15 – 2 = 13, which is correct.
By verifying solutions in this way, you ensure the reliability of your work and avoid errors that could lead to incorrect conclusions. This final step is vital for confidence in the accuracy of your solution and the overall problem-solving process.
Dealing with Fractions in Equations
Fractions in mathematical problems can add complexity, but with the right approach, they can be managed effectively. When fractions appear in an expression, they often need to be eliminated or simplified to make the process of finding the unknown more straightforward. Understanding how to manipulate fractions within an expression is essential for reaching a correct solution.
Eliminating Fractions
One of the most common methods for handling fractions is to eliminate them entirely. This can be done by multiplying both parts of the expression by the denominator of any fraction present. By doing this, fractions are cleared, and the expression becomes easier to manage.
- Example: In 1/3x = 4, multiply both parts by 3 to eliminate the fraction: x = 12
- Example: In 5/8x = 10, multiply both parts by 8: 5x = 80, then solve for x.
Working with Mixed Fractions
When dealing with mixed fractions, it is often useful to first convert them to improper fractions before proceeding. This step simplifies the operations and makes the expressions easier to manipulate.
- Example: In 2 1/2x = 5, first convert 2 1/2 to an improper fraction, 5/2, resulting in 5/2x = 5. Then multiply both parts by 2 to eliminate the fraction: 5x = 10.
By carefully managing fractions and using techniques to eliminate or simplify them, it becomes much easier to work with and solve problems involving fractions. This approach streamlines the process, ensuring more efficient problem-solving and clearer solutions.
Working with Negative Numbers
Negative numbers are a common aspect of many mathematical problems, and knowing how to handle them is essential for obtaining correct results. Whether they appear as part of a larger expression or as the result of an operation, negative values require careful attention. Understanding the rules for adding, subtracting, multiplying, and dividing negative numbers helps to avoid mistakes and ensures accurate solutions.
When performing basic operations with negative numbers, it is important to follow the correct rules. For instance, adding a negative number is the same as subtracting its positive counterpart, while multiplying or dividing two negative numbers results in a positive value. These principles allow for consistent results in a wide variety of problems.
Working with negative numbers requires practice, especially when they are part of more complex problems. By applying the right operations and staying aware of how negative values interact, you can solve problems involving negative numbers with confidence and accuracy.
Solving Equations with Parentheses
Parentheses often appear in mathematical problems, and handling them correctly is essential for achieving accurate results. These symbols indicate that the terms inside need to be simplified or calculated first before proceeding with other operations. Understanding how to deal with parentheses is a key skill in tackling more complex problems.
Distributing to Remove Parentheses

One common method for simplifying expressions involving parentheses is distribution. This involves multiplying each term inside the parentheses by the term outside. By distributing correctly, you can eliminate the parentheses and simplify the expression for easier manipulation.
- Example: In 2(x + 3), multiply both terms inside the parentheses by 2: 2x + 6.
- Example: In 3(2x – 4), distribute 3 to both terms inside: 6x – 12.
Handling Parentheses in Complex Problems
In more complex problems, you may encounter multiple sets of parentheses or need to apply other operations before removing the parentheses. In these cases, it’s important to follow the order of operations–often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction)–to ensure you simplify the expression correctly.
- Example: In 2(3x + 4) + 5, first distribute to get 6x + 8 + 5, then simplify to 6x + 13.
By applying the correct distribution techniques and following the order of operations, you can effectively handle problems that involve parentheses, simplifying them step by step to reveal the solution.
Handling Equations with Decimal Numbers
Decimal numbers often appear in problems that require precise calculations. When dealing with such numbers, it’s crucial to follow the correct steps to ensure accuracy. Whether adding, subtracting, multiplying, or dividing, decimal values can introduce complexity, but with proper techniques, these problems can be solved effectively.
Managing Decimal Addition and Subtraction
When adding or subtracting decimals, alignment is key. Make sure the decimal points are lined up correctly to prevent errors. After placing the decimal points in the same column, proceed with the operation just as you would with whole numbers, ensuring to keep the decimal point in place in the final result.
- Example: 4.5 + 2.75 → Align the decimals: 4.50 + 2.75 = 7.25.
- Example: 8.2 – 3.6 → Align the decimals: 8.20 – 3.60 = 4.60.
Multiplying and Dividing Decimals
For multiplication and division, decimal numbers require a careful approach. When multiplying, count the total number of decimal places in both numbers, and after multiplying the digits, move the decimal point to the left based on the total number of decimal places counted. For division, you may need to adjust the divisor or dividend to eliminate the decimal point before proceeding.
- Example: 3.6 × 2.5 → Multiply as whole numbers: 36 × 25 = 900. The total number of decimal places is 2, so the final result is 9.00.
- Example: 7.2 ÷ 0.4 → Move the decimal to eliminate the fraction: 72 ÷ 4 = 18.
By following these guidelines for decimal operations, you can navigate problems involving decimal numbers with confidence and accuracy, ensuring that your results are both precise and correct.
Solving for More Than One Variable
When dealing with multiple unknowns, the process becomes slightly more intricate. Instead of isolating a single unknown, you need to work with more than one and often require additional steps. This typically involves creating a system of relationships between the different unknowns. Understanding how to manipulate these relationships is essential for finding solutions that satisfy all the conditions in the problem.
To approach problems involving multiple unknowns, start by isolating one unknown at a time. Often, you can express one unknown in terms of the others and then substitute it into another equation. This method allows for step-by-step elimination or substitution, leading to a solution for each unknown.
For example, in a system of two unknowns, you could use substitution or elimination methods to reduce the system to a single equation with one unknown. This allows you to solve for one unknown, then backtrack to find the others. It is important to double-check all steps to ensure the final results are consistent across all equations involved.
Tips for Avoiding Common Mistakes
When working through mathematical problems that involve multiple unknowns, it’s easy to make errors that can lead to incorrect solutions. Being aware of common pitfalls and knowing how to avoid them is crucial for achieving accurate results. Here are some key tips to help minimize mistakes and ensure that your steps lead to the correct solution.
1. Double-Check Your Arithmetic
One of the most frequent mistakes involves simple arithmetic errors. Always check your addition, subtraction, multiplication, and division as you go. A minor miscalculation can throw off the entire process. It’s also helpful to revisit each calculation after completing a few steps to ensure consistency.
2. Keep Track of Negative Signs
Negative numbers are often a source of confusion. Pay close attention to the signs when adding or subtracting terms. Make sure that you’re properly handling negative signs, especially when multiplying or dividing. Misplacing a negative sign can completely change the outcome.
3. Avoid Premature Simplification
Rushing to simplify terms too early can lead to mistakes, especially when dealing with complex expressions. Instead, focus on isolating unknowns and managing each term carefully. Simplify step-by-step to avoid skipping over important calculations.
4. Organize Your Work
Clear organization is key. Write each step methodically and maintain a structured approach. If you find yourself getting stuck or confused, going back to review your work in an organized manner will help you identify where things went wrong.
5. Verify Solutions
After you have determined a solution, always verify it by substituting it back into the original expression. If it doesn’t satisfy the problem, retrace your steps and see where the error might have occurred.
By staying mindful of these tips, you can significantly reduce the likelihood of common errors and ensure that your approach remains logical and methodical throughout the problem-solving process.
Practice Problems for Mastery
To truly master any mathematical skill, consistent practice is essential. Working through problems regularly helps reinforce the concepts, making it easier to spot patterns and apply techniques efficiently. In this section, we will provide a series of practice challenges to help you hone your problem-solving abilities and gain confidence in tackling complex tasks.
Problem 1: Basic Operations with Unknowns

Simplify the following expression and find the unknown:
3x + 4 = 10
Step-by-step, isolate the unknown to determine its value. Double-check each operation to ensure accuracy in your calculations.
Problem 2: Complex Expressions Involving Fractions
Work through this problem involving fractions and solve for the unknown:
1/2x + 3 = 7
Carefully handle the fractions and apply the appropriate operations to isolate the unknown. Don’t forget to check your final result for correctness.
Problem 3: Multiple Terms with Unknowns
In this challenge, you will deal with multiple terms that contain unknowns:
2x + 3 = 4x – 6
Work through the steps of simplifying and isolating the unknown. Remember to keep track of negative numbers and combine like terms where possible.
Problem 4: Parentheses and Distribution
Test your skills with this problem involving parentheses:
3(x + 2) = 18
Use the distributive property to eliminate the parentheses and proceed with solving for the unknown.
Problem 5: Decimal Numbers
This problem involves decimal numbers:
0.5x – 2.3 = 3.7
Handle the decimals carefully and work through the steps to isolate the unknown and solve the problem.
These practice problems are designed to challenge different aspects of the problem-solving process. Work through each one carefully, and remember that mastery comes with repetition and understanding the underlying principles behind each technique.
Real-World Applications of These Equations
The principles used to manipulate and solve algebraic expressions extend far beyond the classroom. In everyday life, many situations require the ability to set up and work through mathematical challenges that involve unknown quantities. By understanding how to manipulate these types of problems, individuals can better navigate a wide range of practical tasks, from budgeting and home improvement to business and engineering. In this section, we will explore how these skills are applied in real-world scenarios.
Financial Planning and Budgeting
One of the most common applications involves managing personal finances. People frequently encounter situations where they need to solve for an unknown value in order to balance their budget, track expenses, or plan for future savings. For example:
- If you know how much you want to save for a specific goal, you might need to calculate how much to save each month given certain interest rates or income constraints.
- Business owners often need to calculate profits or losses by balancing revenue and costs to ensure their companies remain profitable.
Construction and Design Projects
In the field of construction, accurate calculations are vital for designing and building structures. When planning a project, engineers and architects often have to figure out unknown dimensions, materials, or costs. For example:
- Determining how much material is needed to cover a given area, such as flooring or paint, based on dimensions and unit costs.
- Calculating the total structural load by balancing forces applied on various components of the structure.
Engineering and Technology
Engineers rely heavily on mathematical principles when designing products and systems. Whether developing new technologies or improving existing ones, professionals must manipulate complex formulas that involve unknowns. For instance:
- In electrical engineering, calculating the resistance, current, and voltage in circuits requires balancing and simplifying various formulas.
- Mechanical engineers may need to determine the optimal strength-to-weight ratio of materials used in vehicles, aircraft, or machinery.
Understanding and applying mathematical principles like these in the real world help individuals make more informed decisions, improve their work processes, and solve problems efficiently. With practice, these skills can be applied to virtually any field, contributing to both personal and professional success.