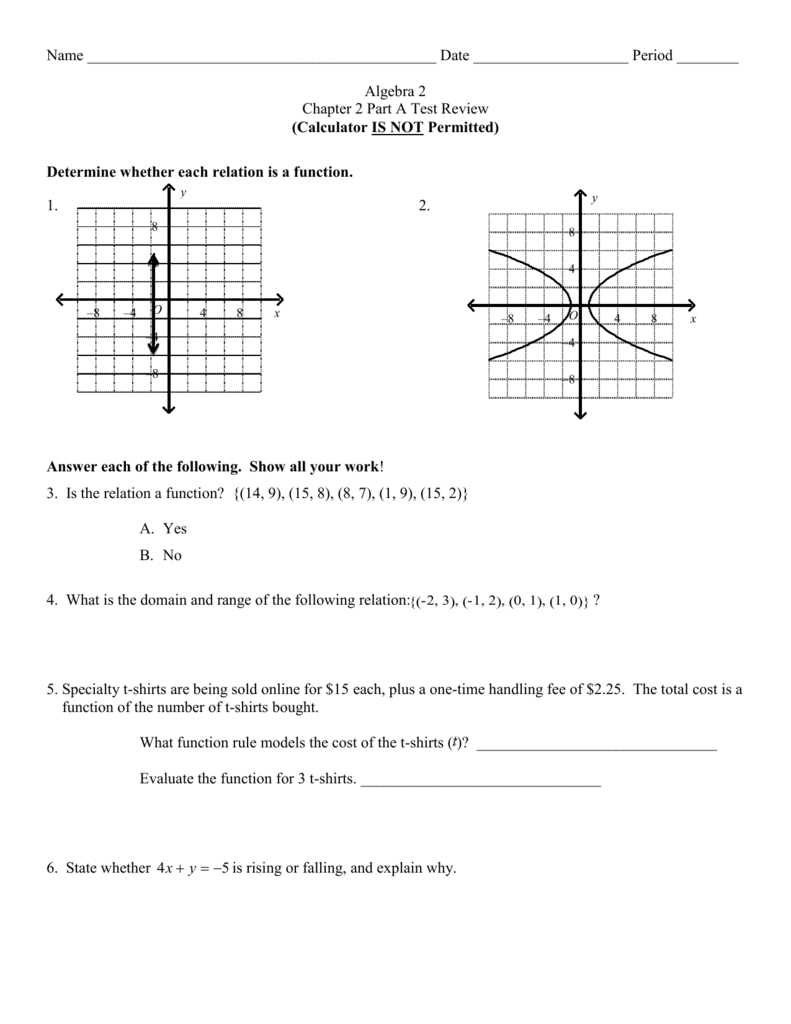
Algebra 2 Chapter 2 Test Review Answers

Mastering advanced mathematical principles can seem challenging, but with a focused approach, you can build a strong foundation. The section ahead will guide you through essential concepts and techniques that are crucial for solving complex problems efficiently.

Focus on core strategies to approach equations, functions, and graphs, ensuring you have a clear understanding of how different topics interconnect. By the end of this guide, you’ll be prepared to tackle even the most demanding problems with confidence.

Explore methods for simplifying expressions, solving systems, and interpreting mathematical models. Each concept is explained with clarity, helping you grasp the underlying principles without feeling overwhelmed. Confidence in these areas is key to succeeding in more advanced topics.

Algebra 2 Chapter 2 Test Review Answers

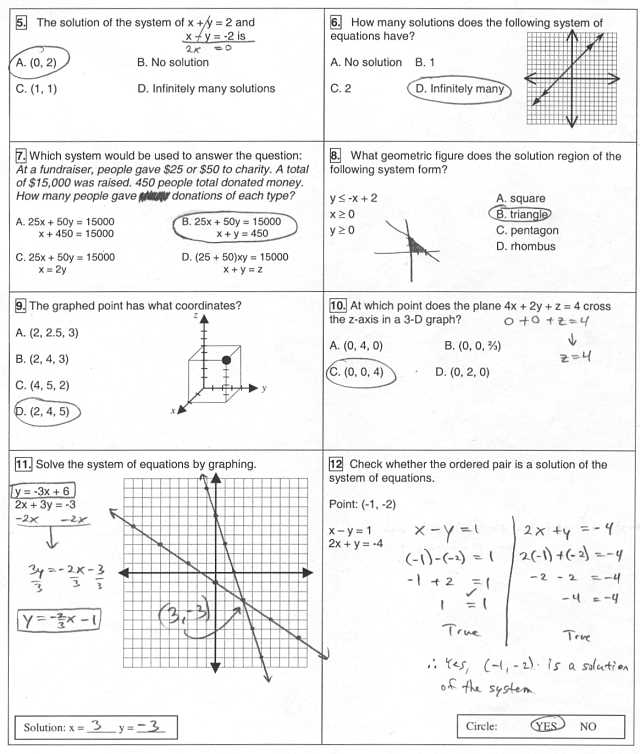
This section focuses on the core methods and techniques necessary for solving a variety of mathematical problems encountered in the second unit. Understanding these methods will allow you to approach different types of equations and expressions with confidence and precision.

In this guide, we break down key strategies for simplifying complex equations, solving systems, and working with functions. Each topic will be explored step by step to ensure clarity and comprehension. Here’s what you’ll learn:

• How to identify and solve quadratic equations effectively
• Key approaches for factoring polynomials and expressions
• Strategies for solving systems of linear equations
• Methods for simplifying rational and radical expressions
• Understanding the graphical representation of equations

By reviewing these strategies and techniques, you will gain the confidence to tackle a variety of problems and achieve success. Let’s dive deeper into each concept and build a solid understanding that will help you solve more challenging problems in the future.

Key Concepts in Chapter 2

In this section, we focus on the fundamental ideas and techniques that are essential for understanding more advanced mathematical topics. Mastery of these concepts is crucial for solving a wide range of problems efficiently and accurately. The core principles covered here lay the foundation for tackling various types of equations and functions.

Understanding Equations and Expressions

One of the main focuses is on recognizing different types of equations and learning effective methods for solving them. You will be introduced to:

• Identifying linear and quadratic relationships
• Solving simple and complex equations through substitution or elimination
• Factoring techniques for simplifying expressions

Working with Functions and Graphs

Another key aspect involves exploring how mathematical functions behave and are represented visually. Understanding how to:

• Graph different types of functions such as parabolas and lines
• Interpret and analyze the properties of graphs, including intercepts and slopes
• Use transformations to manipulate graphs and understand shifts

Grasping these concepts is essential for moving forward in more advanced mathematical studies and applying these techniques to real-world problems.

Understanding Quadratic Functions

Quadratic functions are essential in mathematics and are widely used in various applications. These functions represent relationships that form a U-shaped curve when graphed, called a parabola. Understanding their structure and behavior is crucial for solving many types of problems, from simple equations to more complex applications in physics and economics.

Key Features of Quadratic Functions

When studying quadratic functions, it is important to recognize their key features and how to manipulate them. The main aspects to focus on include:

• The vertex: The highest or lowest point of the parabola, depending on the orientation of the curve.
• The axis of symmetry: A vertical line that divides the parabola into two identical halves.
• The y-intercept: The point where the graph crosses the y-axis.
• The roots or solutions: The x-values where the function equals zero, representing the points where the graph intersects the x-axis.

Graphing and Solving Quadratic Equations

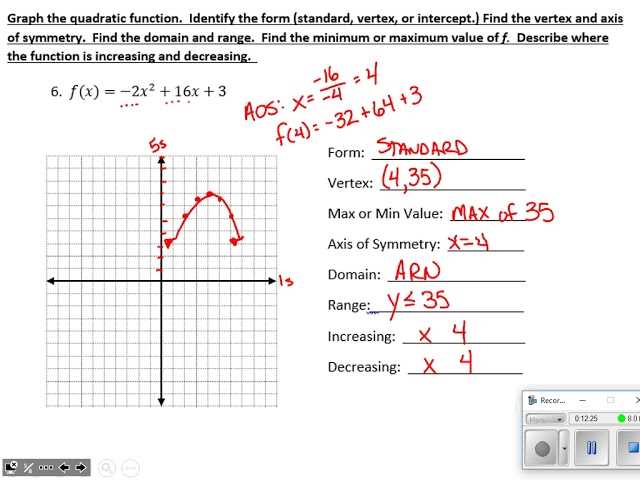
Once the key features are understood, the next step is graphing and solving quadratic equations. Here are the main methods used:

• Factoring: Breaking down the quadratic expression into simpler binomials to find the roots.
• Using the quadratic formula: A formula that provides the solutions to any quadratic equation, even when factoring is not possible.
• Completing the square: A method that involves manipulating the equation to create a perfect square trinomial, making it easier to solve.

Mastering these techniques will enable you to graph quadratic functions and solve equations with ease, paving the way for more advanced studies in mathematics and other fields.

Solving Systems of Equations

Solving systems of equations involves finding the values of variables that satisfy multiple equations simultaneously. These problems are common in various fields, such as economics and engineering, where multiple conditions must be met at the same time. Understanding how to solve these systems effectively is key to solving real-world problems.

There are several methods for solving systems of equations, each with its strengths depending on the type of problem you encounter. The primary techniques include:

• Graphing: This method involves plotting both equations on the same coordinate plane and finding their point of intersection. It’s especially useful for visualizing the solution.
• Substitution: In this approach, you solve one equation for a variable and substitute that expression into the other equation to solve for the remaining variable.
• Elimination: This technique involves adding or subtracting the equations to eliminate one of the variables, making it easier to solve for the other variable.

Each method has its applications depending on the given problem, and mastering them will give you the flexibility to approach different systems confidently and efficiently.

Factoring Polynomials Effectively

Factoring polynomials is a critical skill for simplifying expressions and solving equations. It involves breaking down complex expressions into simpler components, making them easier to work with. Mastering this technique allows you to solve problems more efficiently and uncover solutions that might otherwise be hidden within the complexity of the original equation.

To factor polynomials effectively, it’s important to recognize common patterns and apply appropriate methods. Some key strategies include:

• Greatest Common Factor (GCF): Always begin by identifying and factoring out the greatest common factor from all terms in the polynomial.
• Factoring by Grouping: This method works well when the polynomial has four terms, allowing you to group terms in pairs and factor out common factors from each group.
• Trinomial Factoring: This involves factoring quadratics of the form ax² + bx + c, often using the middle-term factorization method to find two binomials.
• Difference of Squares: Polynomials of the form a² – b² can be factored into (a + b)(a – b), which simplifies the expression significantly.

By practicing these strategies, you can develop a strong understanding of how to break down complex expressions and solve problems with greater ease and accuracy.

Exploring Rational Expressions

Rational expressions involve fractions where both the numerator and denominator are polynomials. Understanding how to simplify, manipulate, and solve these types of expressions is essential for solving more advanced problems in mathematics. Mastering rational expressions allows you to deal with equations involving fractions efficiently and ensures accuracy in solving real-world problems that require such equations.

When working with rational expressions, it is crucial to know how to:

• Simplify: Cancel out common factors in the numerator and denominator to reduce the expression to its simplest form.
• Multiply and divide: When performing these operations, treat the rational expressions like regular fractions by multiplying or dividing the numerators and denominators.
• Add and subtract: Find a common denominator before combining the terms in the numerator.
• Identify restrictions: Be aware of any values that would cause division by zero in the denominator, as these are not allowed.

By learning these techniques, you will be able to approach problems involving rational expressions with confidence and solve them quickly and accurately.

Working with Radical Expressions

Radical expressions involve roots, such as square roots or cube roots, and are a common part of many mathematical problems. Understanding how to simplify and manipulate these expressions is essential for solving equations that involve irrational numbers. Mastery of radical expressions opens the door to tackling more complex problems and ensures accuracy when working with functions that include roots.

Simplifying Radical Expressions

One of the first steps in working with radical expressions is simplifying them. To do this effectively, you need to:

• Factor the radicand: Break down the expression under the root (called the radicand) into its prime factors, then simplify the root by pulling out square numbers or perfect cubes.
• Rationalize the denominator: When a radical expression appears in the denominator, multiply both the numerator and denominator by a suitable radical to eliminate the root from the denominator.

Operations with Radical Expressions

In addition to simplifying, you must also know how to perform various operations with radical expressions:

• Add and subtract: Combine like terms, meaning radicals that have the same index and radicand.
• Multiply and divide: When multiplying, multiply the radicands together. When dividing, divide the radicands, simplifying where possible.

By practicing these techniques, you will be able to handle more complex radical expressions and solve related problems with confidence and precision.

Graphing Parabolas and Their Properties

Graphing parabolas involves plotting U-shaped curves that represent quadratic functions. These curves are symmetrical and have distinct features that make them unique. Understanding how to graph them and identify their key properties is essential for solving a variety of mathematical problems involving quadratic relationships.

Key Features of Parabolas

When graphing a parabola, there are several important characteristics to identify. These include:

• Vertex: The highest or lowest point on the parabola, depending on its orientation.
• Axis of Symmetry: A vertical line that divides the parabola into two mirror-image halves, passing through the vertex.
• Direction of Opening: Parabolas can open upward or downward, which is determined by the sign of the leading coefficient in the quadratic equation.
• Intercepts: The points where the graph intersects the x-axis and y-axis, known as the x-intercepts (roots) and y-intercept.

Graphing Techniques

To graph a parabola accurately, follow these steps:

• Find the vertex: Use the formula x = -b / 2a to find the x-coordinate, and substitute it into the equation to find the y-coordinate.
• Plot the axis of symmetry: Draw a vertical line through the vertex to help visualize the parabola’s symmetry.
• Determine the direction of opening: Check the coefficient of the squared term in the quadratic equation. If positive, the parabola opens upwards; if negative, it opens downwards.
• Identify intercepts: Solve for the values where the function equals zero to find the x-intercepts, and set x = 0 to find the y-intercept.

By understanding these fundamental concepts and techniques, you can graph parabolas and analyze their properties with greater ease and precision.

Identifying Roots of Equations

Identifying the roots of an equation is crucial for understanding the solutions to that equation. These roots are the values that satisfy the equation, making them essential for solving problems in various mathematical contexts. By finding the roots, you uncover the points where the equation equals zero, helping to solve and interpret the underlying relationships in the problem.

Methods for Finding Roots

There are several methods for identifying the roots of an equation, depending on the form of the equation. The primary techniques include:

• Factoring: Break the equation into simpler terms, allowing you to solve for the roots by setting each factor equal to zero.
• Quadratic Formula: For quadratic equations, use the formula x = (-b ± √(b² – 4ac)) / 2a to calculate the roots.
• Graphing: Plot the equation on a coordinate plane and identify the x-intercepts, which represent the roots of the equation.
• Completing the Square: This method involves manipulating the equation to form a perfect square trinomial, making it easier to solve for the roots.

Example of Finding Roots

Let’s consider a simple quadratic equation and demonstrate the process of finding its roots using different methods:

Method	Steps	Solution
Factoring	Factor the equation into two binomials, then set each factor equal to zero.	For x² – 5x + 6 = 0, the roots are x = 2 and x = 3.
Quadratic Formula	Use the quadratic formula: x = (-(-5) ± √((-5)² – 4(1)(6))) / 2(1).	For x² – 5x + 6 = 0, the roots are x = 2 and x = 3.
Graphing	Plot the equation y = x² – 5x + 6 and find the x-intercepts.	The x-intercepts are x = 2 and x = 3.

By using the appropriate method, you can easily identify the roots of an equation, which is a fundamental step in solving many mathematical problems.

Solving Inequalities in Algebra

Solving inequalities involves determining the set of values that satisfy a given relationship between variables. Unlike equations, inequalities express a range of possible solutions rather than a single value. Mastering how to manipulate inequalities is essential for understanding and solving many types of mathematical problems that describe real-world situations, such as limits, constraints, or comparisons between quantities.

To solve an inequality, you follow similar steps to those used for equations, with a few key differences. When you multiply or divide both sides of an inequality by a negative number, you must reverse the direction of the inequality symbol. Understanding this concept is crucial to ensuring the correct solution set.

Common methods for solving inequalities include:

• Isolation of the variable: Like solving equations, the goal is to isolate the variable on one side of the inequality, simplifying the expression step by step.
• Combining like terms: You may need to combine like terms to reduce the inequality to a simpler form, making it easier to solve.
• Graphical representation: For certain inequalities, graphing can help visualize the solution set, especially when working with linear or quadratic inequalities.

By understanding these techniques and applying them correctly, you can efficiently solve inequalities and interpret their solutions in various contexts.

Quadratic Formula and Its Use

The quadratic formula is a powerful tool for solving certain types of equations. It allows you to find the solutions to equations that involve squared terms, regardless of whether the equation factors neatly. This formula provides an efficient way to solve for the variable when other methods, such as factoring or completing the square, are difficult or impossible to apply.

Understanding the Formula

The general form of the quadratic formula is:

x = (-b ± √(b² – 4ac)) / 2a

In this equation, a, b, and c represent the coefficients of the quadratic equation ax² + bx + c = 0. By substituting the values of a, b, and c into the formula, you can calculate the solutions for x.

When to Use the Quadratic Formula

This formula is especially useful when the quadratic equation does not factor easily. It is also the go-to method for solving equations with complex or irrational solutions. By applying the quadratic formula, you can find one or two solutions, depending on the value of the discriminant (b² – 4ac), which determines whether the solutions are real or complex.

When the discriminant is:

• Positive: Two distinct real solutions exist.
• Zero: One real solution exists.
• Negative: Two complex (non-real) solutions exist.

By understanding how to use the quadratic formula, you can confidently solve equations that might otherwise seem challenging.

Operations with Complex Numbers

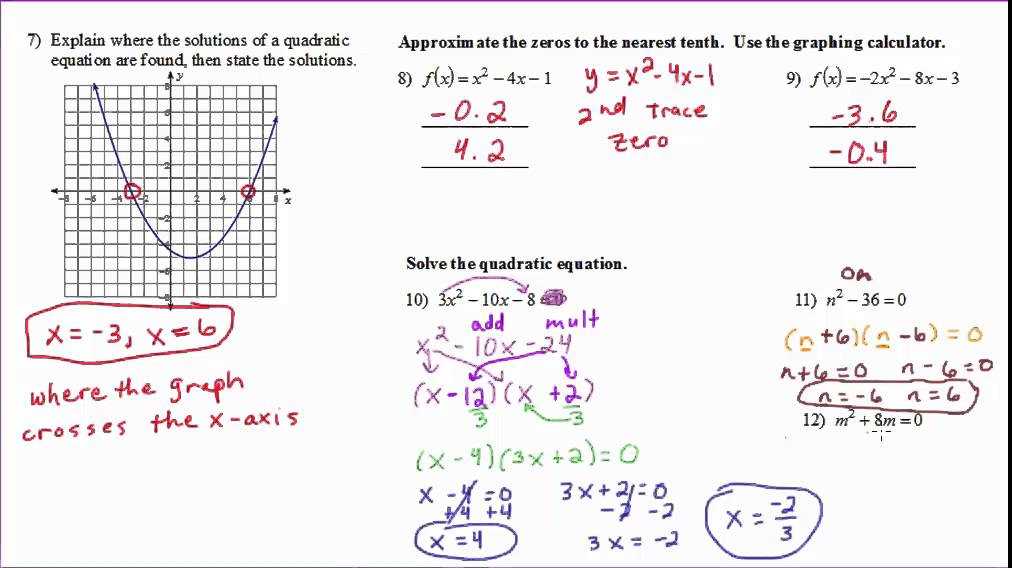
Working with complex numbers involves performing various mathematical operations such as addition, subtraction, multiplication, and division. These numbers include both real and imaginary components, which require different rules compared to regular numbers. Understanding how to handle these operations is crucial for solving problems that involve quantities beyond the real number line.

When adding or subtracting complex numbers, you combine the real parts and the imaginary parts separately. This process is similar to working with polynomials, where like terms are grouped together.

For multiplication, the distributive property is used, but there is a special rule: when multiplying the imaginary unit (often denoted as i), you remember that i² = -1. This rule helps simplify expressions and avoid confusion when working with powers of i.

Division of complex numbers requires a method called “multiplying by the conjugate.” This technique eliminates the imaginary part in the denominator, simplifying the expression. The conjugate of a complex number a + bi is a – bi.

By mastering these basic operations, you can confidently manipulate complex numbers in various mathematical and real-world applications.

Reviewing Absolute Value Functions

Absolute value functions are essential tools in mathematics, providing a way to measure distance from zero on a number line, regardless of direction. These functions involve expressions that transform any negative values into their positive counterparts, making them useful in various real-world scenarios where only the magnitude of a quantity matters, not its sign.

Key Features of Absolute Value Functions

An absolute value function typically takes the form f(x) = |x|, where x is the variable. The graph of such a function is always V-shaped, with the vertex at the origin if there are no transformations. The function is symmetric about the vertical line through the vertex and increases as you move away from the origin in either direction.

Transformations of Absolute Value Functions

When transformations are applied to the basic absolute value function, they alter its graph in different ways. These transformations can include shifts, stretches, and reflections:

• Vertical Shifts: Adding or subtracting a constant to the function will shift the graph up or down.
• Horizontal Shifts: Adding or subtracting inside the absolute value expression will shift the graph left or right.
• Reflections: A negative coefficient in front of the absolute value will reflect the graph over the x-axis.
• Stretching and Compressing: Multiplying the entire function by a constant greater than one stretches the graph, while multiplying by a constant between zero and one compresses it.

By understanding these properties and transformations, one can work with absolute value functions to model and solve a wide range of mathematical problems.

Understanding Functions and Their Graphs

Functions are fundamental in mathematics, providing a relationship between two sets where each input corresponds to exactly one output. The graph of a function visually represents this relationship, showing how the output changes as the input varies. By understanding functions and interpreting their graphs, you gain valuable insight into how different mathematical models behave in various contexts.

Key Characteristics of Functions

When examining a function, it’s important to focus on several key aspects:

• Domain: The set of all possible inputs (x-values) for which the function is defined.
• Range: The set of all possible outputs (y-values) the function can produce.
• Continuity: Whether the function’s graph is unbroken, meaning there are no gaps, jumps, or holes in the graph.
• Increasing and Decreasing Intervals: Sections of the graph where the function’s value increases or decreases as the input increases.

Interpreting Graphs of Functions

Graphs of functions provide a powerful visual representation of how the function behaves. Here are some key features to look for:

• Intercepts: The points where the graph crosses the x-axis (x-intercepts) and the y-axis (y-intercepts).
• Slope: The steepness of the graph, indicating how rapidly the output changes as the input changes.
• Symmetry: Some functions, such as even and odd functions, exhibit symmetry about specific axes, which can provide insights into their behavior.
• Asymptotes: Lines that the graph approaches but never reaches, often found in rational functions or logarithmic graphs.

By studying both the properties of functions and their graphical representations, you can solve a wide range of mathematical problems and better understand how different types of functions behave.

Converting Between Different Forms

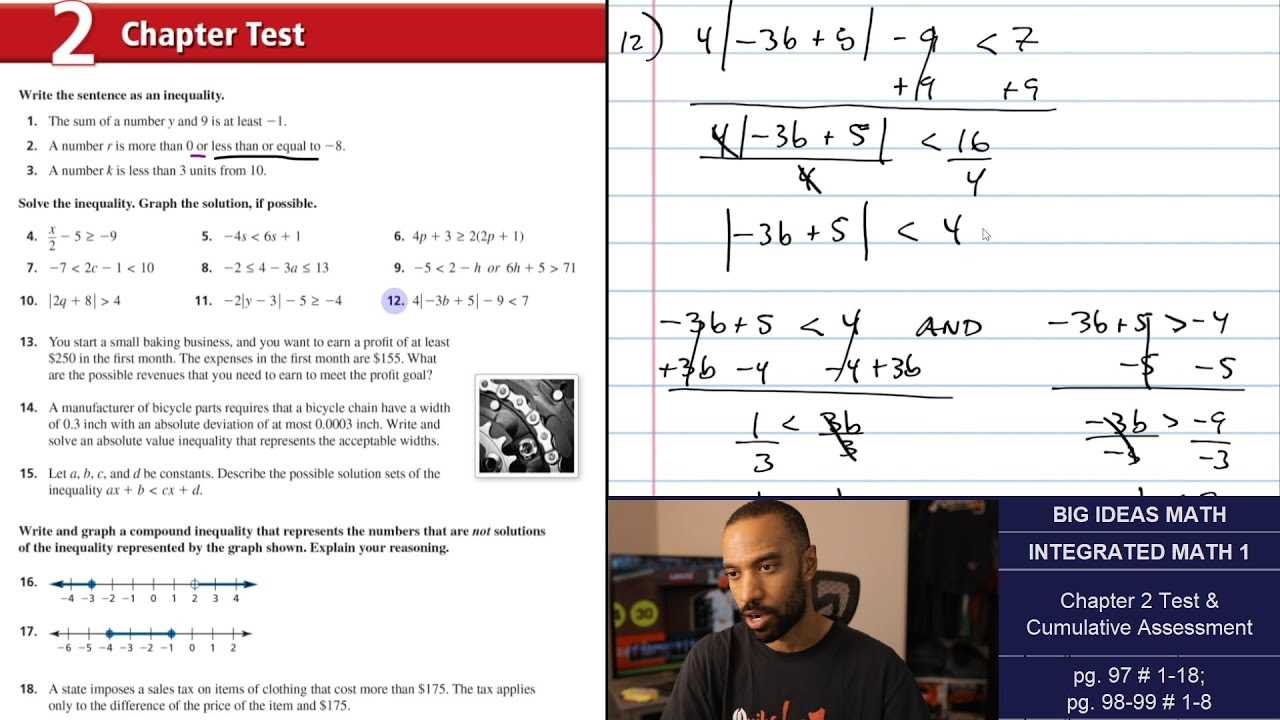
Mathematical expressions can often be represented in various ways, and understanding how to convert between different forms is an essential skill. Whether it’s rewriting an equation in standard or vertex form, or simplifying a rational expression, mastering these transformations helps in solving problems more efficiently and understanding the underlying relationships. The ability to switch between forms offers flexibility in tackling complex mathematical tasks and provides deeper insight into the structure of equations.

Key Forms of Equations

Common types of equations that require conversions include quadratic equations, linear equations, and rational expressions. The most frequently used forms include:

• Standard Form: Often used for linear and quadratic equations, where the highest degree term is first, followed by the others in descending order.
• Vertex Form: A more useful form for graphing, as it highlights the vertex of a parabola.
• Factored Form: Often used in quadratic equations to find roots or zeros of the function.
• Intercept Form: Focuses on the x-intercepts of a function, providing useful information about the solutions.

Converting Quadratic Equations

Converting quadratic equations between different forms is particularly useful for solving them in the most efficient way. Below is a general overview of how to convert a quadratic equation from standard form to vertex form, and vice versa.

Standard Form	Vertex Form
y = ax² + bx + c	y = a(x – h)² + k
To convert from standard form to vertex form, use the method of completing the square. This involves manipulating the equation to create a perfect square trinomial and isolating the constant term.

Similarly, understanding how to convert between other forms of equations–such as from factored form to standard form–can simplify solving for variables, graphing, or finding intercepts. The process of converting forms is a useful tool in algebraic manipulation that ensures you can approach problems from multiple angles.

Mastering Word Problems in Algebra

Word problems can often feel daunting, but with the right approach, they can be broken down into manageable steps. The key is to translate the written description into a mathematical equation that can be solved. By identifying the variables, understanding the relationships between them, and using appropriate operations, you can solve these problems efficiently. Mastering this skill not only enhances problem-solving abilities but also strengthens overall mathematical reasoning.

To tackle word problems effectively, follow these steps:

• Read Carefully: Start by reading the problem thoroughly. Pay attention to the details, especially the units and conditions given in the question.
• Define Variables: Assign variables to the unknowns in the problem. This makes it easier to formulate an equation that represents the situation.
• Set Up an Equation: Translate the relationships described in the problem into a mathematical expression or equation. Look for keywords like “sum,” “difference,” “product,” or “ratio” to guide you.
• Solve the Equation: Use the appropriate methods, whether it’s solving linear equations, working with quadratic expressions, or applying other techniques, to find the value of the variable.
• Check the Solution: After finding a solution, revisit the problem to ensure that your answer makes sense in the context of the real-world scenario.

With practice, you’ll be able to approach word problems with confidence, quickly identifying the necessary steps and solving them with ease. This ability to translate real-life situations into mathematical expressions is not only useful in academic settings but also in everyday decision-making and analysis.

Test Taking Strategies for Success

Successfully navigating an assessment requires more than just knowledge of the subject matter. It involves preparation, time management, and strategic thinking to maximize performance. By applying effective techniques, you can approach the exam with confidence and increase the likelihood of achieving your best results. Here are some key strategies to help you succeed in any evaluative situation.

One of the most important aspects of performing well is proper preparation. This means reviewing all relevant material well in advance, practicing problem-solving, and understanding the format of the assessment. However, equally important is how you handle the actual exam day. Below are some useful tips to optimize your performance:

Strategy	Tips
Time Management	Divide your time according to the number of questions. Start with the ones you are most confident in to build momentum.
Read Instructions Carefully	Ensure you understand what each question is asking before beginning. Misinterpreting instructions can lead to avoidable mistakes.
Prioritize Easy Questions	Answer the questions you find easiest first, then move on to more difficult ones. This helps build confidence and saves time for more complex problems.
Stay Calm	If you encounter a difficult problem, take a deep breath, and move on to the next one. Come back later with a clear mind.
Review Your Work	If time allows, go over your answers at the end. Double-check for any careless mistakes or missed questions.

By incorporating these strategies into your study and test-taking habits, you can reduce stress, improve focus, and increase your chances of performing well. Whether you’re taking a quiz, a final exam, or any other form of assessment, having a clear approach will ensure you’re ready for any challenge that comes your way.