CPM Algebra 2 Textbook Answers and Solutions

Understanding complex mathematical principles is essential for academic success. In this section, we will explore effective strategies to tackle various problems found in intermediate-level math courses. With detailed methods and solutions, you can deepen your comprehension and sharpen your problem-solving skills.

By following a structured approach to solving equations, you will develop a clear understanding of the key ideas that govern mathematical reasoning. This guide provides valuable techniques that simplify difficult topics, enabling students to gain confidence and achieve better results in their studies.

CPM Algebra 2 Textbook Overview

This section provides a comprehensive guide to the structure and key components of an intermediate-level mathematics course. It focuses on critical topics that challenge students, offering insights into the logical flow and connections between concepts. Understanding these core ideas is essential for mastering the subject and applying them effectively to solve various types of problems.

Core Structure of the Course

The course is designed to build on foundational mathematical skills while introducing more complex ideas. Each unit is carefully structured to help students progress from basic to advanced techniques, with the goal of fostering both conceptual understanding and practical application. Throughout the course, students encounter a mix of problem-solving exercises, real-world examples, and theoretical lessons.

Key Topics Covered

Throughout the lessons, students will explore a wide array of subjects, from equations and functions to graphing and advanced problem-solving strategies. Below is a table summarizing some of the primary topics covered in the course:

Topic	Description
Equations and Inequalities	Focus on solving linear and quadratic equations and inequalities, providing essential tools for more complex problems.
Functions	Introduction to different types of functions, their properties, and how they relate to real-world applications.
Graphing	Techniques for graphing functions and interpreting data, a critical skill for visualizing mathematical concepts.
Word Problems	Practical exercises that apply mathematical theory to solve real-life scenarios.
Polynomials and Rational Expressions	In-depth exploration of polynomial functions, factoring, and rational expressions.

These key topics form the backbone of the course, allowing students to gradually expand their knowledge and refine their mathematical skills. With a structured approach and consistent practice, students can achieve a deep understanding of the material.

Key Concepts in Algebra 2

At the heart of this course are several fundamental principles that form the basis of more complex mathematical reasoning. These concepts are designed to challenge and develop students’ critical thinking skills, enabling them to approach problems from various angles. Mastering these key ideas is crucial for building a strong mathematical foundation that can be applied across a wide range of subjects.

One of the central themes is the understanding of functions, which describe relationships between variables and are essential for solving many types of equations. The ability to manipulate and graph these functions is a vital skill. Another major focus is on polynomials and their properties, including how to factor and solve higher-degree equations. Students also delve into rational expressions, learning to simplify and perform operations involving fractions with algebraic terms.

Another important area covered is the study of systems of equations, where multiple equations are solved simultaneously to find a common solution. This concept is fundamental in both theoretical and applied mathematics. Furthermore, students are introduced to more advanced techniques for solving quadratic equations, which have widespread applications in fields such as physics and engineering.

Understanding CPM Algebra 2 Format

The structure of this course is designed to promote both independent learning and collaborative problem solving. Students are encouraged to engage with the material not only through individual practice but also by discussing and sharing ideas with peers. This approach helps reinforce understanding and allows for a deeper grasp of complex mathematical concepts.

Each lesson is carefully crafted to introduce new ideas in a progressive manner, starting with simpler topics and gradually moving toward more advanced material. The format emphasizes the importance of understanding the process behind problem-solving rather than just memorizing formulas. As a result, students are trained to think critically and apply mathematical concepts in a variety of contexts.

Additionally, the course often includes group activities and discussions, providing students with opportunities to learn from each other and clarify difficult concepts. This collaborative learning model is an essential part of the format, encouraging students to explain their reasoning and approach problems from multiple perspectives.

How to Use Textbook Answers Effectively

Utilizing solutions from your course material can be a powerful tool for reinforcing your understanding, but it’s essential to approach them in the right way. Simply copying the steps or results won’t help in the long run. Instead, focus on understanding the reasoning behind each solution and the steps taken to reach the conclusion.

Start by attempting to solve a problem on your own first. If you get stuck, consult the solution for guidance. Pay close attention to how each part of the problem is broken down, and identify the key concepts used in the solution. This will help you recognize patterns and methods that can be applied to similar problems.

Next, use the solutions as a way to check your work. After completing a problem, compare your method with the provided solution. If your approach differs, examine why the given solution works better and how you can adjust your method in future problems. It’s important to view solutions not just as a way to get the right answer, but as a learning tool that helps you refine your problem-solving process.

Finally, practice consistently by working on additional problems. The more you practice, the more you’ll internalize the methods and strategies required to solve complex problems independently. Use the provided solutions to clarify doubts, but always strive to enhance your critical thinking and analytical skills.

Common Algebra 2 Problem Types Explained

In this section, we will explore the most common types of problems you will encounter in intermediate-level math. Understanding these problem types will help you develop strategies for solving them effectively. By recognizing the structure and methods used to tackle these problems, you can improve your approach and achieve better results in your studies.

1. Solving Equations

Equations are at the core of many problems in this course. They can vary in complexity, from simple linear equations to more intricate quadratic and higher-order expressions. The key to solving these equations lies in understanding the properties of operations and applying the correct methods for isolating variables.

• Linear Equations: Solving for a variable in equations like 2x + 5 = 15.
• Quadratic Equations: Using factoring, completing the square, or the quadratic formula to solve equations like x² + 5x + 6 = 0.
• Rational Equations: Solving equations that involve fractions, such as (2/x) + 3 = 5.

2. Graphing Functions

Graphing functions helps visualize mathematical relationships between variables. By plotting equations on a coordinate plane, you can identify key features such as intercepts, slopes, and behavior at different points.

• Linear Graphs: Plotting straight lines based on equations like y = 2x + 3.
• Quadratic Graphs: Identifying the shape of parabolas from equations like y = x² – 4x + 3.
• Exponential Graphs: Understanding exponential growth or decay, for example y = 2^x.

3. Word Problems

Word problems require you to translate real-life situations into mathematical expressions. This often involves setting up equations based on the information given and solving for the unknown values.

• Cost and Revenue Problems: Solving problems that involve profit, cost, and revenue, such as calculating the break-even point.
• Distance, Rate, and Time: Problems involving the relationship between speed, time, and distance.
• Mixture Problems: Finding the concentration of mixtures, like determining the ratio of two substances in a solution.

Step-by-Step Solutions for Algebra 2

Understanding the process behind solving complex problems is essential for mastering intermediate mathematics. By breaking down problems into smaller, manageable steps, students can gain a clearer understanding of the methods used to reach a solution. This structured approach allows for more efficient learning and ensures that students build a strong foundation in problem-solving techniques.

General Problem-Solving Approach

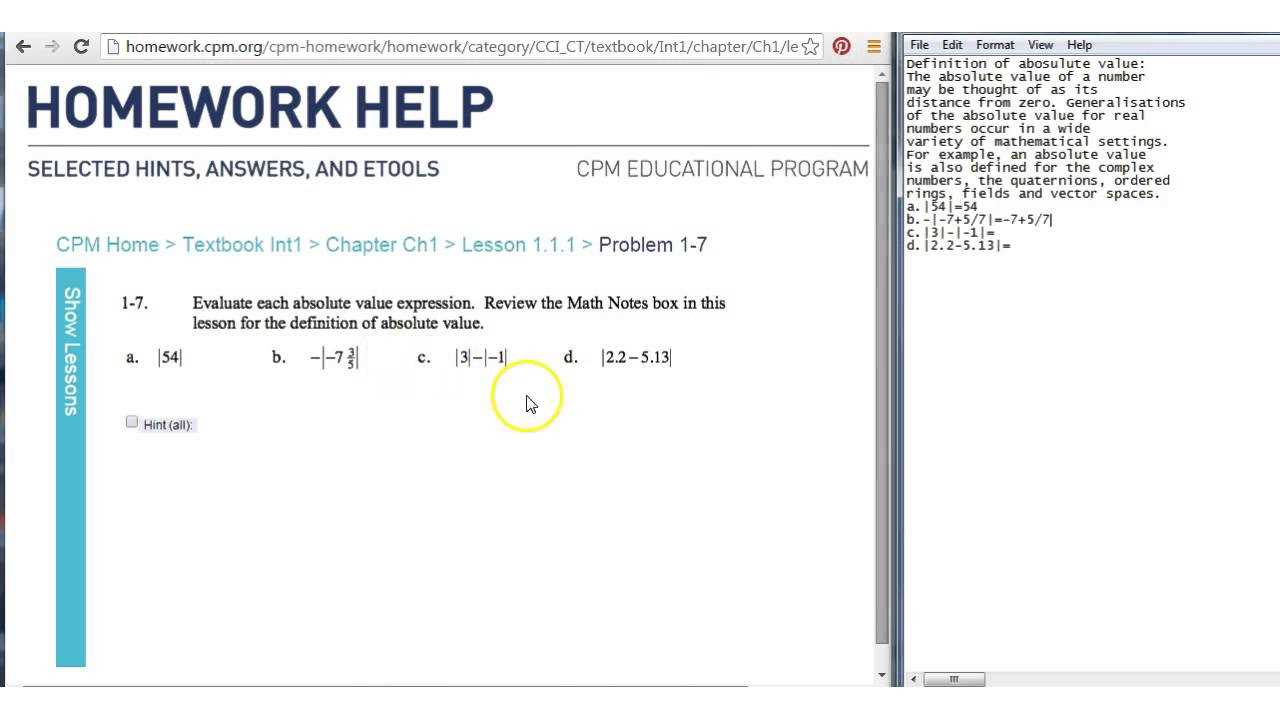
The first step in solving any problem is to carefully analyze the given information. Identifying the type of problem will guide the methods you need to apply. From there, you will systematically work through each stage of the solution, applying the appropriate operations and checking your work along the way.

Step	Action
Step 1	Read and understand the problem. Identify the given variables and what is being asked.
Step 2	Set up an equation or expression based on the information provided.
Step 3	Apply appropriate methods to solve the equation, such as factoring, substitution, or using formulas.
Step 4	Verify the solution by substituting it back into the original problem to check for correctness.
Step 5	Review the process to ensure there are no errors and that the solution makes sense in the context of the problem.

Example Problem and Solution

Let’s go through a step-by-step example of solving a quadratic equation:

Problem: Solve for x in the equation x² – 5x + 6 = 0.

Step 1: Identify the equation type. This is a quadratic equation, which can be factored.

Step 2: Factor the quadratic expression: (x – 2)(x – 3) = 0.

Step 3: Set each factor equal to zero: x – 2 = 0 or x – 3 = 0.

Step 4: Solve each equation: x = 2 or x = 3.

Step 5: Verify the solutions by substituting them back into the original equation. Both solutions satisfy the equation, so x = 2 and x = 3 are correct.

Mastering Word Problems in Algebra

Word problems often seem challenging, but with the right approach, they can become an opportunity to apply mathematical concepts in real-life scenarios. The key to solving these problems effectively lies in translating the language of the problem into mathematical expressions. By carefully breaking down the given information and identifying the relationships between variables, you can develop a strategy to find the solution.

The first step in tackling a word problem is to thoroughly read the question and understand what is being asked. Pay attention to key phrases and numbers, as these will guide you in forming an equation or expression. Next, define your variables–assign symbols to the unknowns you need to solve for. This helps in organizing the information and clarifying the problem.

Once you’ve set up the variables, the next step is to form an equation or a system of equations based on the problem’s conditions. After that, apply the appropriate mathematical techniques to solve the equation, such as simplifying, factoring, or using formulas. Lastly, always check your solution by substituting it back into the original problem to ensure it makes sense in the given context.

Tips for Success:

• Break it down: Separate the problem into smaller, more manageable parts.
• Look for patterns: Identify familiar structures, such as rate problems or mixtures, to apply known techniques.
• Draw diagrams: Visualizing the problem can often make relationships clearer, especially in geometry-based word problems.
• Check units: Always ensure that your units are consistent throughout the problem.

With practice, solving word problems becomes easier and more intuitive. As you gain confidence in translating verbal descriptions into mathematical expressions, you’ll improve both your problem-solving skills and your ability to understand complex real-world scenarios.

Understanding Functions in Algebra 2

In intermediate mathematics, functions are a fundamental concept that connects inputs to outputs through a defined rule. Functions are used to model relationships between variables and help describe patterns, behaviors, and changes in various contexts. Mastering functions is key to solving many types of problems and understanding how different quantities interact.

A function can be thought of as a machine: you input a value (often represented by x), and the function produces an output (represented by y) based on a specific rule. The relationship between these inputs and outputs is the core concept of a function.

Key Characteristics of Functions

• Domain: The set of all possible input values for which the function is defined.
• Range: The set of all possible output values produced by the function.
• Function Notation: Functions are typically written in the form f(x) = y, where f represents the function, and x is the input.
• One-to-One Function: A function where each input maps to a unique output, and each output has one corresponding input.

Types of Functions

There are several types of functions that you will encounter, each with its own set of rules and characteristics. Here are some of the most common ones:

• Linear Functions: Represented by equations of the form y = mx + b, where m is the slope and b is the y-intercept. These functions graph as straight lines.
• Quadratic Functions: Represented by equations like y = ax² + bx + c, these functions graph as parabolas, either opening upwards or downwards.
• Exponential Functions: Functions of the form y = ab^x, where b is a constant. These functions model rapid growth or decay.
• Rational Functions: Functions involving fractions, where the numerator and denominator are both polynomials, such as f(x) = (p(x))/(q(x)).

Understanding these types of functions, their properties, and how to manipulate them is essential for solving more complex problems and building a strong foundation in mathematics.

Graphing and Analyzing Equations

Graphing equations is an essential skill in mathematics that allows you to visualize relationships between variables. By plotting the equation on a coordinate plane, you can gain insights into the behavior of the function, identify key features such as intercepts, slopes, and asymptotes, and understand how changes in the equation affect the graph. Analyzing these graphs helps you interpret and solve real-world problems more effectively.

To graph an equation, it’s important to understand its structure and what each term represents. The graph provides a visual representation of the mathematical relationship, which can be analyzed to uncover key characteristics. Whether you’re working with linear, quadratic, or more complex equations, the graph will offer a valuable perspective on how the equation behaves across different values of the independent variable.

Key Steps in Graphing Equations

• Identify the equation type: Determine if the equation is linear, quadratic, or another type. This will guide the approach to graphing.
• Calculate key points: For many functions, begin by calculating points that are easy to plot, such as intercepts or known values of the function.
• Plot the points: Mark the points on the coordinate plane, paying attention to the scale and accuracy of the plot.
• Draw the graph: Connect the points smoothly, following the shape of the curve or line that best represents the equation.

Analyzing Graphs of Equations

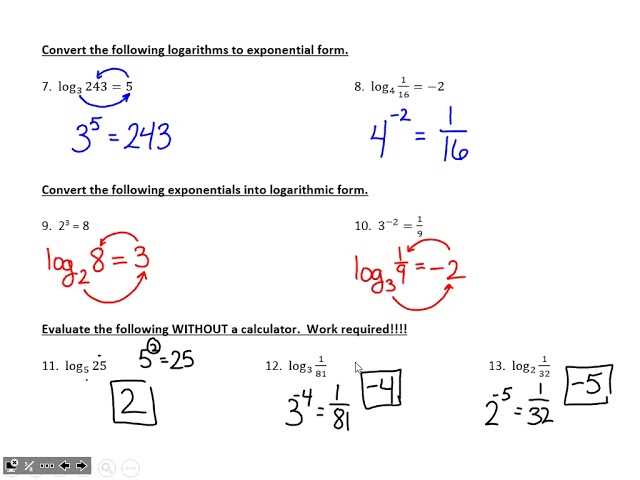
Once you’ve graphed the equation, the next step is to analyze its key features. Some important elements to look for include:

• Intercepts: The points where the graph crosses the x-axis and y-axis are crucial for understanding the solutions to the equation.
• Slopes and Curvature: For linear equations, the slope indicates the steepness of the line, while for quadratic and other curves, the curvature provides information about how the graph behaves.
• Asymptotes: For certain types of functions, such as rational functions, analyzing asymptotes helps in understanding the function’s behavior at extreme values.
• Symmetry: Many functions have symmetry, which can be used to simplify the graphing process and make predictions about the behavior of the function.

By carefully analyzing the graph, you can interpret the equation’s behavior, make predictions, and solve problems more efficiently. This process is vital in both theoretical mathematics and practical applications.

Algebra 2 Word Problem Strategies

Word problems often present challenges by requiring the translation of a real-life situation into a mathematical equation. These types of problems test your ability to interpret the information given, identify relevant variables, and apply the appropriate techniques to find a solution. Effective strategies can help break down these complex problems into manageable steps and ensure a clear approach to finding the correct answer.

Approaching word problems requires patience and practice, as well as a logical step-by-step method. By following certain strategies, you can better understand the problem’s requirements, set up equations correctly, and interpret the results in a meaningful way. This section outlines key strategies for solving word problems in an organized and efficient manner.

Steps for Solving Word Problems

• Read the problem carefully: Start by reading the problem multiple times to ensure you fully understand what is being asked.
• Identify the variables: Determine which quantities in the problem are unknown and assign variables to them, such as x, y, or other appropriate symbols.
• Translate into an equation: Convert the words into mathematical expressions, making sure the relationship between the variables reflects the situation described in the problem.
• Set up and solve the equation: Solve the equation for the unknown variable using appropriate techniques, such as substitution, elimination, or factoring.
• Check the solution: After solving, plug the solution back into the original context to ensure it makes sense and satisfies the conditions of the problem.

Common Strategies for Word Problems

• Draw a diagram or chart: For problems involving geometric shapes or comparisons, drawing a visual representation can help clarify relationships and make it easier to set up the equation.
• Use logical assumptions: In some cases, making reasonable assumptions based on the context can simplify the problem. For example, assume the total number of items is consistent if the problem doesn’t specify otherwise.
• Look for keywords: Certain words, like “total,” “difference,” or “product,” often indicate specific operations (addition, subtraction, multiplication, etc.), which can guide the equation setup.
• Work backward: If the problem is complex, sometimes working backward from the desired outcome can be an effective approach to solving it.

Mastering these strategies will increase confidence and efficiency when tackling word problems, helping you approach each one with a systematic and methodical mindset.

Common Mistakes in Algebra 2

Mathematical problems often come with their own set of challenges, and errors can occur at various stages of solving an equation. Recognizing and understanding the common pitfalls can significantly improve problem-solving skills. By identifying frequent mistakes, students can learn how to avoid them and develop a more effective approach to solving equations.

In many cases, mistakes are made during the interpretation of the problem, the setup of the equation, or in the arithmetic operations themselves. Understanding these common errors and knowing how to address them is crucial for success in more advanced topics. Below are some of the most frequent errors encountered and how to avoid them.

Common Mistakes	How to Avoid Them
Incorrectly simplifying expressions: Often, students mistakenly combine terms incorrectly, leading to wrong results.	Carefully check each step of the simplification process and ensure that like terms are combined properly.
Sign errors: Incorrectly handling positive and negative signs, especially during multiplication or division, can lead to incorrect solutions.	Always double-check sign operations, and use parentheses where needed to avoid confusion.
Forgetting to distribute: Failing to apply the distributive property correctly is a common mistake, especially in binomial expressions.	Ensure to distribute each term through the parentheses correctly and check each multiplication carefully.
Misunderstanding variable relationships: Not properly understanding how variables relate to each other within an equation can lead to incorrect assumptions.	Take time to interpret word problems accurately and assign variables correctly before proceeding with the calculations.
Skipping steps: Rushing through problems and skipping intermediary steps may result in missing crucial information.	Work through problems systematically and write out every step, no matter how simple it seems.

By recognizing these common mistakes and taking steps to avoid them, students can improve their mathematical skills and become more confident in their ability to solve problems accurately.

Tips for Solving Complex Equations

Solving intricate mathematical equations can often feel overwhelming, especially when they involve multiple variables or advanced operations. However, by following a strategic approach and applying key problem-solving techniques, you can simplify even the most complex expressions. Understanding how to break down these equations into smaller, manageable steps is crucial to finding the correct solution efficiently.

In this section, we will explore several tips and methods to help you navigate through complex problems. Whether dealing with higher-degree polynomials, systems of equations, or irrational numbers, these strategies will guide you in applying the right techniques to achieve accurate results.

• Break the problem into smaller parts: For complex equations, it’s helpful to divide the problem into simpler sub-problems. Solve each part step by step to avoid being overwhelmed.
• Isolate the variable: In many cases, isolating the variable on one side of the equation can make it easier to solve. Use algebraic manipulation to simplify the expression before solving.
• Check for common factors: Before proceeding with more complicated operations, see if you can factor out common terms. This often makes solving the equation easier.
• Use substitution or elimination: For systems of equations, substitution and elimination methods can help you eliminate variables and solve the equations more efficiently.
• Consider the order of operations: Always follow the correct order of operations (PEMDAS) when solving. This ensures that each step is performed in the correct sequence, reducing the chance of errors.
• Look for patterns: In some cases, recognizing patterns in the equation can help you identify shortcuts or identify specific strategies for solving.
• Work with equivalent forms: Sometimes, rewriting the equation in a different form–such as converting a radical to an exponent or factoring a quadratic–can make the solution process smoother.

By consistently applying these strategies, you can tackle even the most challenging problems with confidence, leading to more accurate and efficient solutions.

How to Check Your Answers

Once you’ve worked through a problem, it’s essential to verify that your solution is correct. Double-checking your results helps ensure accuracy and prevents mistakes from going unnoticed. Whether you are solving an equation, graphing a function, or analyzing a word problem, a few key strategies can help you confirm that your solution is reliable.

In this section, we will explore several methods for reviewing your work to ensure that you’ve arrived at the correct result. These techniques will help you avoid common pitfalls and increase your confidence in your solutions.

• Substitute the solution back into the original equation: This is one of the most straightforward ways to check your answer. If the original equation holds true when you plug in your solution, then it’s likely correct.
• Use estimation: If the problem involves large numbers or complex calculations, approximate the solution to see if it aligns with your final answer. Estimation can help catch obvious errors.
• Cross-check with a different method: If you solved the problem using a particular approach, try using a different method to verify your result. For example, if you solved using substitution, try elimination or vice versa.
• Check for consistency: Ensure that your solution makes sense within the context of the problem. If the answer seems unreasonable or doesn’t fit the parameters of the problem, go back and review your steps.
• Review your work step by step: Go through each step you took in solving the problem. Check for calculation errors, missed signs, or incorrect assumptions that may have led to an incorrect solution.
• Graph your solution: For problems involving equations of lines, curves, or inequalities, graphing your solution can visually confirm whether your answer is correct. If the graph matches your expectations, your solution is likely accurate.

By applying these verification techniques, you can ensure that your solutions are correct and gain greater confidence in your mathematical skills.

Additional Resources for Mastery

To further improve your skills and deepen your understanding of complex mathematical concepts, there are numerous resources available. These tools can provide you with extra practice, different approaches, and expert explanations that will help you solidify your knowledge. Whether you prefer online platforms, textbooks, or interactive tools, there are plenty of options to support your learning journey.

Here are some helpful resources to enhance your mastery of mathematical topics:

• Online Courses: Websites like Khan Academy and Coursera offer free and paid courses that cover a wide range of topics, from basic equations to advanced problem-solving techniques.
• Tutoring Services: If you need personalized guidance, consider reaching out to online tutoring platforms such as Chegg or Wyzant. A tutor can help clarify difficult concepts and provide one-on-one assistance.
• Interactive Tools: Graphing calculators, such as GeoGebra or Desmos, can help you visualize equations, explore functions, and better understand the relationships between variables.
• Practice Problem Websites: Platforms like IXL or Brilliant offer interactive practice problems that help reinforce key concepts. These sites often provide immediate feedback, allowing you to track your progress and identify areas for improvement.
• Math Forums and Communities: Engage with others in online forums like Stack Exchange or Reddit’s math communities. These forums are great for asking questions, exploring different problem-solving techniques, and learning from experienced individuals.
• Study Guides and Workbooks: Investing in comprehensive study guides or workbooks, such as those from Barron’s or The Princeton Review, can provide additional explanations and practice exercises to enhance your skills.

By utilizing these resources, you can access a variety of learning methods and further develop your problem-solving abilities. Combining different tools and strategies will help you build confidence and improve your overall mathematical proficiency.

Practice Exercises for Mastery

Practicing mathematical problems regularly is essential to mastering any subject. By working through a variety of exercises, you can enhance your understanding, build problem-solving skills, and prepare for more advanced topics. Consistent practice allows you to become familiar with different problem types and reinforces key concepts.

Here are some effective practice exercises that will help improve your skills and deepen your knowledge:

• Equation Solving: Focus on solving linear, quadratic, and rational equations. This will help you become proficient in isolating variables and simplifying expressions.
• Function Evaluation: Work on evaluating different types of functions. This will improve your understanding of function notation, domain, range, and transformations.
• Graphing Exercises: Practice plotting equations and analyzing their graphs. Focus on identifying key features such as intercepts, slopes, and asymptotes.
• Word Problems: Solve real-world problems that require the application of mathematical principles. Word problems test your ability to translate a situation into a mathematical equation.
• Factoring Problems: Work on factoring polynomials and solving problems that involve factoring, such as solving quadratic equations by factoring or using the difference of squares.
• Systems of Equations: Practice solving systems of equations using various methods, including substitution, elimination, and graphing.
• Inequalities: Focus on solving and graphing inequalities. Understanding how to work with inequalities is crucial for analyzing mathematical relationships.
• Exponential and Logarithmic Functions: Practice solving exponential and logarithmic equations to strengthen your understanding of these important concepts.

By working through these exercises, you can build a strong foundation and improve your mathematical abilities. The key is consistency–make sure to practice regularly and challenge yourself with a variety of problems to continue progressing.

Preparing for Algebra 2 Exams

Effective preparation for exams requires a strategic approach to ensure a deep understanding of the material. By reviewing key concepts, practicing problem-solving techniques, and identifying areas that need further attention, you can increase your confidence and performance on the test. Structured revision and targeted practice are essential to mastering the material and achieving success.

Here are some practical strategies to help you prepare for your exams:

• Create a Study Schedule: Organize your study time to cover all the key topics systematically. Allocate more time to areas where you feel less confident and allow for regular breaks to avoid burnout.
• Review Past Assignments: Going over previous assignments, quizzes, and practice problems can help reinforce what you have already learned and highlight any gaps in understanding.
• Focus on Key Concepts: Prioritize reviewing important topics such as functions, equations, graphing, and inequalities. These concepts are likely to appear frequently on exams.
• Practice Problem-Solving: Regularly work through a variety of practice problems, especially those that are similar to what you might encounter on the exam. This will help reinforce your problem-solving skills and improve your speed.
• Use Study Groups: Collaborating with peers can provide different perspectives and enhance understanding. You can quiz each other, explain difficult concepts, and clarify any doubts.
• Test Yourself: Simulate exam conditions by taking timed practice tests. This will help you get used to managing your time during the exam and reduce anxiety.
• Review Mistakes: After completing practice problems, make sure to review any mistakes carefully. Understanding where you went wrong is crucial for improving and avoiding the same errors in the future.
• Stay Organized: Keep your notes, formulas, and key concepts neatly organized for easy reference. This will help you quickly find important information when reviewing or practicing.
• Relax and Stay Positive: While it’s important to study diligently, it’s equally essential to stay calm and positive. Take time for relaxation and ensure you’re well-rested before the exam day.

By following these strategies and staying consistent with your preparation, you can approach your exam with greater confidence and perform to the best of your ability. Good preparation is key to mastering the material and achieving your academic goals.