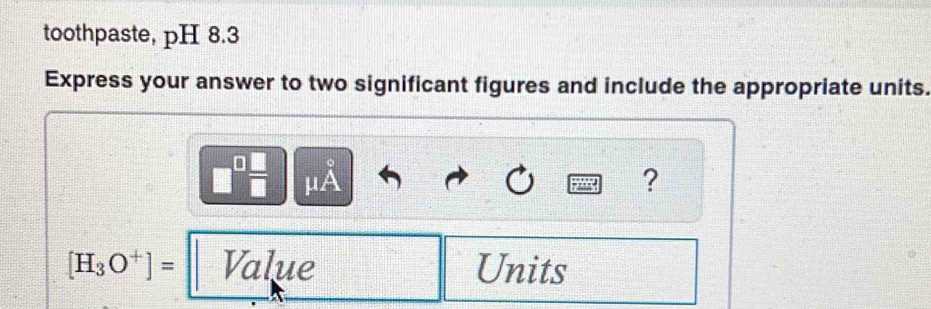
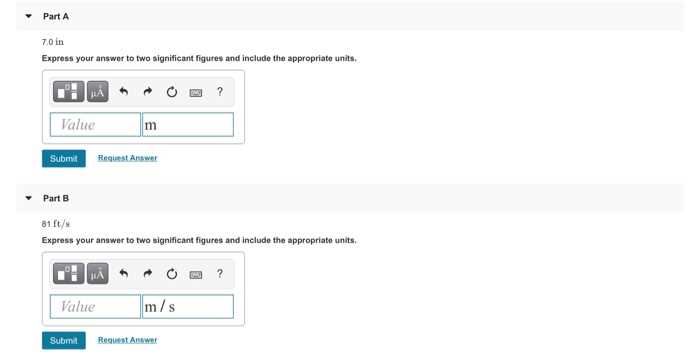
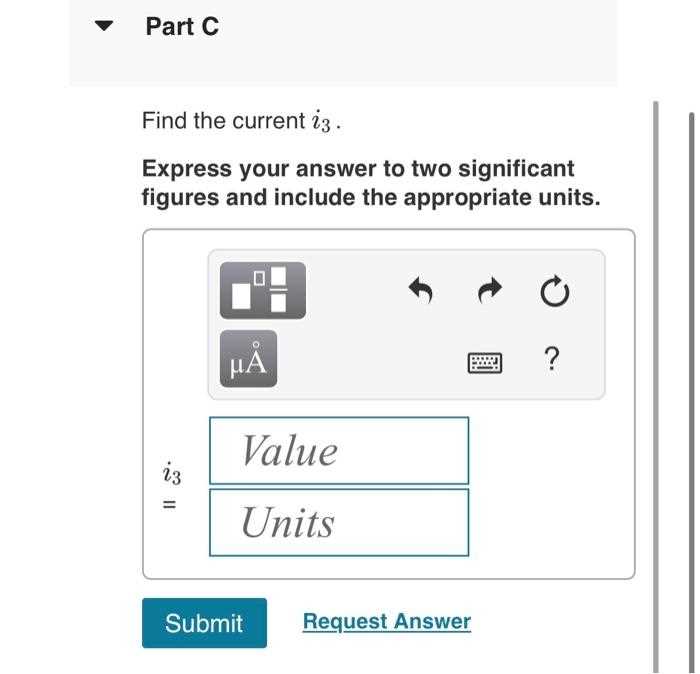
Express Answer to Two Significant Figures and Include Units
When dealing with numerical results, it is essential to represent them with precision while ensuring they are easily understood. This involves rounding numbers to a specified level of precision and using measurement labels correctly. The way results are presented can significantly affect how they are interpreted in scientific and technical fields.
Clarity is a crucial factor in any calculation, especially when discussing values derived from measurements. Whether working with basic arithmetic or complex scientific data, ensuring that the numbers reflect the desired level of accuracy is vital. Furthermore, indicating the right measurement labels allows others to understand the scale or magnitude of the values provided.
By adhering to established practices for rounding and labeling, individuals can communicate their results with confidence, avoiding confusion and promoting reliability in their work. Precision in these areas also supports consistency across various disciplines, ensuring that all calculations are both correct and meaningful.
Understanding Significant Figures in Measurements
When working with numerical data, it’s crucial to convey not only the raw value but also the level of precision of that value. Precision refers to how exact a measurement is, reflecting the limitations of the tools used and the method of obtaining data. It’s essential to determine the correct degree of detail to present in a result, especially when the value might have implications for further calculations or scientific analysis.
What Determines Precision in Measurements?
Several factors influence how much detail should be included in a number. These factors include:
- The resolution of the measuring instrument.
- The method of measurement used and the consistency of results.
- Any conventions or rules established in the specific field of study.
Why Precision Matters
Maintaining consistent accuracy in numerical results prevents misinterpretations and ensures that calculations are reliable. Whether conducting experiments or analyzing statistical data, knowing how to round numbers correctly and communicate their precision helps avoid errors in further work. In many cases, overstating the precision could imply a false level of accuracy, while understating it might not reflect the actual reliability of the data.
What Are Significant Figures and Why They Matter?
In any scientific or technical measurement, it is important to understand how much precision is reflected in the result. Not all numbers are created with the same level of accuracy, and knowing how to convey that difference is essential. Properly presenting values ensures that they accurately represent the precision of the measurements from which they were derived.
Understanding Precision in Measurements
When we perform any calculation, we must consider how much we can trust the numbers involved. Precision is often limited by the measuring tools or techniques, which means that some digits in a result are more reliable than others. These reliable digits, along with their associated uncertainty, form the core of how we communicate data effectively.
Why Correct Representation Matters
Accurately reflecting precision prevents confusion in scientific work, ensuring that others can replicate experiments or calculations with the same expectations. Misrepresenting the level of precision can lead to incorrect conclusions or decisions. It is important to follow established rules for rounding and reporting data, particularly when values play a role in further analysis or calculations.
How to Round Numbers to Two Significant Figures
Rounding values to a specified level of precision is an essential skill in both everyday calculations and scientific work. In many cases, it’s necessary to reduce a number to just the most important digits while maintaining its accuracy as much as possible. This process helps simplify numbers, making them easier to work with while ensuring they still reflect the underlying measurement’s reliability.
Steps for Rounding to the Correct Precision
To round any number, begin by identifying the digits that carry the most meaningful information. These are typically the first non-zero digits in the value. From there, follow these steps:
- Locate the first two non-zero digits in the number.
- Look at the next digit to determine whether to round up or leave it unchanged.
- If the next digit is 5 or higher, increase the last retained digit by one.
- If the next digit is less than 5, leave the retained digits as they are.
Examples of Rounding in Practice
For instance, rounding 0.04356 to two meaningful digits results in 0.044. Meanwhile, rounding 135.789 to the same level of precision would yield 140. These examples show how rounding simplifies numbers without introducing unnecessary detail, yet still keeps the core information intact.
Importance of Correct Units in Scientific Answers
In any scientific or mathematical context, it is essential to communicate not just the raw numbers but also the scale or measurement system they represent. Without proper measurement labels, even the most accurate data can become misleading or confusing. These labels provide context, helping to ensure that results are understood clearly and used correctly in further analysis.
Why Measurement Labels Are Crucial
Correctly indicating measurement labels is vital for a number of reasons:
- They prevent confusion about the scale of the result (e.g., meters versus kilometers).
- They ensure consistency in scientific communication, allowing others to replicate experiments or calculations accurately.
- They highlight the precision of the measurement, helping others understand the reliability of the data.
Common Mistakes in Labeling Measurements
Failure to include or misrepresent measurement labels can lead to significant errors, such as:
- Incorrect conversions between measurement systems (e.g., mixing inches with centimeters).
- Misinterpretation of the size or scale of values, leading to erroneous conclusions.
- Confusion between quantities that share similar numerical values but differ in units, such as weight versus mass.
Ensuring correct labeling of measurements is a simple yet crucial step that supports clarity, accuracy, and proper interpretation of scientific data.
Common Mistakes in Using Significant Figures
When working with numerical data, it’s easy to make errors in how precision is conveyed, especially when rounding or performing calculations. These mistakes can lead to inaccurate results and misunderstandings in scientific and technical contexts. Being aware of common pitfalls helps ensure that numbers are represented correctly, with the appropriate level of detail and accuracy.
Overstating or Understating Precision
One of the most frequent errors is either overstating or understating the level of accuracy. Some common mistakes include:
- Adding unnecessary digits that imply a higher precision than what was originally measured.
- Removing digits from a value, which can suggest a lack of precision when it’s not warranted.
Incorrect Application of Rounding Rules
Rounding numbers can be tricky, and applying the wrong rules leads to imprecise results. Common issues include:
- Rounding too early in a calculation, which can propagate errors throughout the process.
- Using improper rounding methods, such as rounding up when it should be down, or vice versa.
- Failing to adjust numbers based on the correct place value when rounding.
These mistakes can significantly affect the reliability of results, especially when the numbers are used in further calculations or comparisons. Ensuring that rounding is done correctly and consistently is crucial to maintaining the integrity of data.
How to Handle Zeros in Significant Figures

Zeros can be tricky when determining the level of precision in a number. They can either be part of the meaningful digits or serve as placeholders depending on their position within the value. Understanding how to treat zeros correctly is essential for presenting numbers with the right level of detail.
Leading Zeros
Leading zeros are zeros that appear before the first non-zero digit in a number. These digits are not considered significant because they do not affect the value of the number. For example, in the number 0.00456, the leading zeros do not contribute to the precision and are ignored when determining the meaningful digits.
Captive Zeros
Captive zeros, which appear between non-zero digits, are always significant. For instance, in the number 2003, the zero is significant because it falls between the digits “2” and “3,” making it an integral part of the value. It reflects the precision of the measurement.
Trailing Zeros
Trailing zeros, or zeros that appear after non-zero digits, have different significance depending on the presence of a decimal point. If there is a decimal point, trailing zeros are considered significant. For example, in 45.00, the trailing zeros are meaningful and indicate that the number is accurate to two decimal places. However, in a number like 4500, the zeros may not be considered significant unless specifically indicated by a decimal point or other notation.
Correctly interpreting zeros ensures that numbers accurately reflect their level of precision, preventing confusion or misrepresentation of data.
Significant Figures in Different Mathematical Operations
When performing mathematical calculations, the precision of the result depends on the precision of the numbers involved. Each type of operation, whether it’s addition, subtraction, multiplication, or division, affects how the final result should be rounded or presented. Understanding the rules for handling precision during each type of calculation ensures that the outcome reflects the correct degree of certainty.
Rules for Operations
In general, the number of meaningful digits in the result of an operation is determined by the precision of the numbers used. Here’s a brief overview of how precision is handled in various operations:
| Operation | Rule |
|---|---|
| Multiplication or Division | The result should have the same number of meaningful digits as the number with the least precision in the operation. |
| Addition or Subtraction | The result should have the same number of decimal places as the number with the least precision in the operation. |
Examples of Operations
To illustrate the rules, consider the following examples:
- Multiplying 4.56 × 1.4 gives a result of 6.38, but since 1.4 has only two meaningful digits, the answer should be rounded to 6.4.
- Adding 23.456 + 1.2 gives 24.656, but since 1.2 has only one decimal place, the final result should be rounded to 24.7.
Following these rules ensures that calculations are consistent with the precision of the data and accurately reflect the degree of uncertainty inherent in the original measurements.
Why Accuracy in Units Is Crucial
When working with numerical data, measurement labels are as important as the values themselves. Whether dealing with length, mass, time, or any other physical quantity, using the correct measurement system ensures that results are both interpretable and reliable. Inaccurate or inconsistent labeling can lead to serious errors, misinterpretations, and even incorrect conclusions.
Consequences of Incorrect Measurement Labels
Incorrect or inconsistent measurement labels can have far-reaching consequences. Some of the issues include:
- Confusion in communication, especially when sharing results across different fields or countries with varying standards.
- Calculation errors due to incompatible measurement systems, leading to discrepancies between results.
- Loss of precision in scientific experiments, where even small differences in units can yield vastly different outcomes.
Ensuring Consistency in Scientific Work
In any scientific or technical field, maintaining consistent measurement labels is essential for ensuring the accuracy and credibility of the work. This can be achieved by:
- Double-checking units in every calculation or experiment.
- Using international standards or clearly stated conventions for measurements.
- Including clear documentation of the units used, particularly in collaborative work or published research.
Accurate labeling reinforces the integrity of scientific data, enabling others to understand, replicate, and trust the findings. Whether in the laboratory, the field, or in mathematical models, precision in units is not just a technical requirement, but a fundamental aspect of clear communication and sound reasoning.
Scientific Notation and Significant Figures
Scientific notation is a method of expressing very large or very small numbers in a more compact form. This technique is particularly useful when dealing with measurements that span a wide range of magnitudes, such as in scientific research or engineering. It allows for easier comparison and manipulation of numbers, while also preserving the precision of the data through a standardized format.
In scientific notation, numbers are expressed as a product of a coefficient and a power of 10. The coefficient typically contains the meaningful digits of the value, while the exponent indicates the magnitude or scale. When using this notation, it’s crucial to maintain the same level of precision, ensuring that the digits presented are consistent with the level of certainty of the original measurements.
The number of digits included in the coefficient reflects the accuracy of the measurement. For example, a value written as 3.45 × 104 implies that only two digits are reliable and should be considered when performing calculations or comparisons. In this way, scientific notation provides a clear and concise way to handle numbers, while ensuring that their precision is accurately communicated.
How to Express Precision with Units
In scientific and technical contexts, conveying the precision of a measurement is just as important as the measurement itself. The level of certainty associated with a value is often indicated by the number of digits used, as well as the measurement label that accompanies it. Precision is not only about how exact a number is, but also how clearly the measurement is communicated through its corresponding unit.
To effectively communicate precision, it is essential to match the number of decimal places or digits to the measurement’s reliability. For example, a length measurement given as 4.56 meters is more precise than 4 meters, as it indicates a greater level of detail. Similarly, the unit plays a crucial role in conveying the context of the measurement. Without the correct unit, even the most precise number can lose its meaning, leading to confusion or misinterpretation.
When working with measurements, it’s important to ensure that both the value and the unit reflect the same level of accuracy. For instance, if a temperature is measured to the nearest degree, the value should not be extended beyond its reliable range. This careful alignment between number and unit ensures that the measurement is communicated clearly and accurately.
Understanding the Rules for Rounding Numbers
Rounding is a key process in simplifying numerical data while maintaining its relevance. Whether you’re working with measurements, financial data, or scientific calculations, rounding ensures that the values are concise and manageable without sacrificing necessary precision. However, it’s important to follow certain rules to ensure consistency and accuracy when reducing the number of digits in a value.
In most cases, rounding involves looking at the digit immediately following the last one you wish to keep. If this digit is 5 or higher, you round the last kept digit up. If it’s lower than 5, you leave the last kept digit unchanged. This basic rule helps standardize results across different contexts, ensuring clarity and comparability.
It’s also essential to consider how many digits should remain after rounding. In some cases, rounding may be necessary to reflect the precision of the measurement or to fit the context of the problem. For example, in scientific work, it’s crucial to round in a way that reflects the accuracy of the instruments used for measurement.
What Units Should Be Used in Calculations?
Choosing the correct unit for calculations is a fundamental aspect of any scientific or mathematical work. The unit of measurement reflects the nature of the quantity being measured and determines how values are interpreted, compared, and used in equations. Using inconsistent or incorrect units can lead to errors and miscalculations, affecting the accuracy of results.
When performing calculations, it’s essential to first ensure that all values are expressed in compatible units. For example, if you’re working with measurements of length, time, or mass, the units must align across the entire equation. This ensures that the final result makes sense and retains the correct meaning.
Common Units in Scientific Calculations
- Length: Meters (m), centimeters (cm), kilometers (km)
- Mass: Kilograms (kg), grams (g), milligrams (mg)
- Time: Seconds (s), minutes (min), hours (h)
- Temperature: Celsius (°C), Kelvin (K), Fahrenheit (°F)
Converting Between Units
Often, different units are used in the same calculation, so it’s necessary to convert between them. For example, converting kilometers to meters or grams to kilograms allows for accurate comparison and computation. Conversion factors, such as 1 kilometer = 1000 meters or 1 kilogram = 1000 grams, are essential tools in ensuring that calculations are correct.
How to Convert Units While Maintaining Precision
When converting between different systems of measurement, it is crucial to ensure that the resulting value retains the same level of accuracy as the original. A unit conversion is not just about changing one measurement to another but also about understanding how that change affects the overall precision of the data. Without proper handling, converting units could lead to loss of significant information or introduce unnecessary errors.
To maintain precision, the conversion factor must be carefully selected, and the number of decimal places or significant digits must be consistent throughout the process. By following proper methods, it is possible to convert values without compromising on their accuracy, ensuring that every step aligns with the intended measurement’s degree of certainty.
Steps for Accurate Unit Conversion
- Identify the units you need to convert and the corresponding conversion factor.
- Use the conversion factor to adjust the value, ensuring that the measurement is expressed in the correct units.
- Round the result to match the required precision, ensuring that no more digits are added than necessary.
- Always check the conversion by performing a reverse conversion to verify the accuracy of the result.
Common Conversion Mistakes to Avoid
- Using incorrect conversion factors: Always ensure that the conversion factor is correct for the units involved.
- Over-rounding: Avoid rounding too early in the process, as this can cause inaccuracies in the final result.
- Not adjusting for significant digits: Ensure that the precision is preserved after converting to the new unit.
Significant Figures in Complex Calculations
When dealing with multi-step mathematical operations, maintaining precision throughout the process is essential. Complex calculations often involve a series of additions, subtractions, multiplications, and divisions, each of which can affect the precision of the final result. The challenge lies in ensuring that each intermediate step preserves the correct level of certainty, which in turn guarantees that the final result is as accurate as possible.
In these scenarios, it is crucial to apply the correct rules for rounding at each step to prevent the propagation of errors. This is particularly important when working with large datasets or performing scientific measurements, where even small inaccuracies can lead to significant deviations in outcomes. Therefore, understanding how to apply rounding rules effectively is key to maintaining reliable results in complex calculations.
Impact of Significant Figures in Engineering
In engineering, precision is a cornerstone of design, analysis, and problem-solving. Whether developing new materials, designing structural components, or conducting simulations, maintaining the correct level of precision throughout calculations is vital for ensuring the reliability and safety of projects. Even minor errors in measurement or calculation can lead to major discrepancies in results, affecting everything from efficiency to structural integrity.
Engineers must be diligent in managing the precision of their data, especially when converting between different measurement systems or combining various calculations. An improper application of precision could result in unsafe designs, costly errors, or faulty systems. This makes understanding how to correctly use precision in calculations a critical skill for engineers across all fields.
Key Considerations in Engineering Calculations
- Ensuring that precision is maintained during each stage of design and testing.
- Adhering to industry standards for measurement accuracy to ensure compatibility across various components and systems.
- Using rounding techniques that reflect the limitations of the tools and methods used in data collection.
Applications of Precision in Engineering Projects
- Creating accurate blueprints and technical specifications for construction and manufacturing.
- Modeling and simulating system behaviors to predict performance under various conditions.
- Optimizing resource use in projects to minimize waste and reduce costs.
How to Check Your Work for Accuracy
Ensuring that calculations and measurements are accurate is an essential step in any technical or scientific task. Without verifying that all steps have been completed correctly, there is a risk of making costly mistakes that could lead to incorrect conclusions or unsafe results. Taking the time to carefully review each step of a process can prevent errors and improve the overall quality of work.
One of the most effective methods for ensuring accuracy is to recheck calculations and measurements after they have been completed. This includes verifying the consistency of units, reviewing intermediate steps, and confirming that all relevant factors have been taken into account. Additionally, cross-referencing results with established standards or known values can help identify discrepancies early in the process.
Methods for Verifying Accuracy
- Double-check calculations: Recalculate important steps to confirm that the results are consistent.
- Review unit conversions: Ensure that all measurements have been converted correctly between different systems.
- Compare with known values: Cross-check results against accepted values or benchmarks to see if they align.
Tips for Improving Precision
- Use tools effectively: Rely on accurate instruments and tools to measure or perform calculations.
- Be systematic: Follow a structured approach to avoid overlooking important details.
- Seek feedback: Have peers or colleagues review your work for additional insight and verification.
Best Practices for Presenting Scientific Answers
When sharing results in scientific or technical contexts, clarity, precision, and consistency are crucial for effective communication. Whether presenting findings in written reports, oral presentations, or digital formats, adhering to established guidelines ensures that information is conveyed accurately and comprehensively. It is essential to make sure that the data provided is understandable to the intended audience, whether they are experts or those with less specialized knowledge.
A key aspect of presenting results is maintaining consistency in how measurements are represented. This includes following standard conventions for rounding, formatting, and using measurements. In addition, explanations should be clear and supported by well-organized evidence to avoid confusion and to enhance the credibility of the work.
Guidelines for Clear Presentation
- Use consistent notation: Stick to widely accepted symbols and formatting rules for clarity and ease of understanding.
- Be mindful of rounding: Avoid over-precision, ensuring that only relevant digits are shown based on the level of confidence in the data.
- Clarify units: Always specify the measurement system (e.g., metric, imperial) and ensure that conversions are accurate when needed.
Improving Communication with Visuals
- Use graphs and charts: Visual aids can make complex data easier to understand and compare.
- Label everything clearly: Every figure, table, and diagram should have appropriate titles and axes labels to prevent ambiguity.
- Provide context: Explain the relevance of data within the broader scope of the research to help the audience grasp its significance.
Tools for Rounding and Converting Units
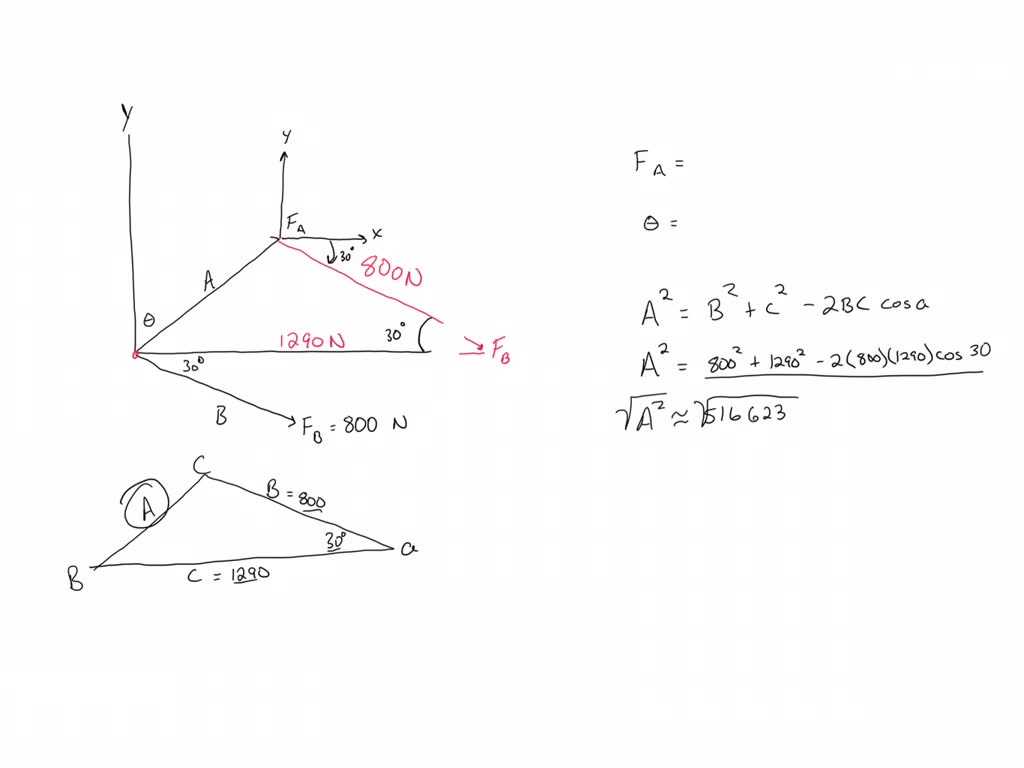
Accurate calculations often require precise rounding and unit conversions. To achieve this, there are a variety of tools available that can help simplify and automate the process. These tools ensure that measurements are expressed correctly, maintaining consistency and precision in scientific, engineering, or everyday applications. Whether using online converters or specialized software, these resources save time and reduce errors in manual calculations.
Rounding tools typically allow users to define how many digits to keep, automatically adjusting the number as needed. Unit conversion tools can handle a wide range of measurement systems, converting everything from length and mass to temperature and time, ensuring that no information is lost during the process.
Commonly Used Tools
| Tool Type | Function | Example Tools |
|---|---|---|
| Rounding Calculators | Helps round numbers to a specified number of decimal places or significant digits. | Online rounding calculators, Excel ROUND function |
| Unit Converters | Converts values between different measurement systems, such as metric to imperial. | UnitConverters.net, Google search (e.g., “5 inches to cm”) |
| Scientific Software | Used for advanced calculations, including automatic rounding and conversion based on specific needs. | MATLAB, Wolfram Alpha |
These tools make it easier to work with complex calculations and ensure that the final results are both accurate and consistent with the required standards.