Algebra Connections Chapter 2 Answers and Solutions

In this section, we delve into the core principles that form the foundation of higher-level problem-solving techniques. These ideas are essential for building a strong mathematical understanding and developing the skills necessary for tackling complex equations and scenarios. With the right approach, even the most challenging problems can be broken down into manageable steps.

We will explore methods for simplifying intricate tasks, focusing on practical applications and strategies that will help you think critically and efficiently. Whether you’re looking to enhance your problem-solving abilities or refine your understanding of various mathematical operations, this guide provides valuable insights into overcoming common obstacles.

Through detailed explanations and examples, you’ll be equipped with the tools to handle a variety of exercises, ensuring a comprehensive grasp of the material. By mastering these techniques, you will gain confidence in your ability to apply these skills in different contexts, setting the stage for continued success in more advanced topics.

Algebra Connections Chapter 2 Overview

This section introduces essential techniques for solving complex problems that rely on fundamental mathematical concepts. It emphasizes understanding the relationships between various elements and how they interact to form solutions. By mastering these core principles, learners are equipped to approach more advanced challenges with greater ease.

Throughout this guide, key strategies for problem breakdown and simplification are highlighted. You will gain insight into how abstract ideas can be translated into clear steps, making seemingly difficult tasks more manageable. This approach not only enhances understanding but also builds confidence in tackling a wide range of mathematical situations.

Core Concepts Covered

The following table summarizes the primary topics and skills explored in this section:

Topic	Key Skills
Understanding Variables	Identifying and manipulating unknowns in equations
Equation Simplification	Breaking down complex expressions into simpler forms
Solving Linear Equations	Applying step-by-step methods to find solutions
Word Problems	Translating real-world scenarios into mathematical expressions

Problem-Solving Techniques

Key to mastering this material is the ability to break down and tackle problems logically. By applying systematic methods, students can efficiently navigate through even the most intricate exercises. This section will guide you through various strategies, ensuring you have the tools to approach new problems with confidence and clarity.

Key Concepts from Chapter 2

This section focuses on the fundamental principles that form the foundation of solving mathematical problems effectively. It explores the relationships between variables, operations, and equations, enabling learners to develop a deeper understanding of how to manipulate and solve different types of mathematical expressions. Mastering these core concepts is essential for progressing to more advanced problem-solving tasks.

Throughout this guide, particular attention is given to simplifying complex equations, recognizing patterns, and using logical reasoning to approach different types of exercises. The concepts introduced in this section are designed to enhance both analytical thinking and practical application, helping learners approach challenges with confidence and precision.

By grasping these fundamental ideas, you will build a solid base for tackling more intricate mathematical topics and problems, ensuring greater success in future learning. Whether you’re refining basic techniques or gaining insight into more complex methods, these core principles are indispensable for continued progress.

Understanding Problem-Solving Strategies

Effective problem-solving requires a clear approach to break down complex tasks into manageable steps. Understanding the underlying strategies is key to navigating through mathematical challenges efficiently. This section focuses on techniques that help identify the most effective methods for solving different types of problems, whether simple or intricate.

By following structured strategies, learners can develop a step-by-step process to approach exercises systematically. These strategies not only enhance your problem-solving skills but also foster a deeper understanding of mathematical relationships and operations.

Essential Problem-Solving Techniques

The following methods are crucial for solving various types of problems:

• Identify the problem: Carefully read and understand what is being asked before proceeding with any calculations.
• Break the problem into smaller steps: Divide complex problems into smaller, more manageable tasks to make the solution process clearer.
• Look for patterns: Recognize trends or common elements within the problem that can lead to a more efficient solution.
• Use logical reasoning: Apply logical steps based on known rules or principles to guide you toward the solution.
• Check your work: After solving, verify the solution by reviewing each step to ensure the answer is accurate and consistent.

Practical Tips for Success

In addition to following the core strategies, there are practical approaches that can further improve your problem-solving ability:

1. Practice regularly: The more problems you solve, the better you’ll get at recognizing patterns and applying strategies.
2. Stay organized: Keep your work neat and structured, as disorganized steps can lead to confusion and errors.
3. Ask for help when needed: Don’t hesitate to reach out to others if you’re stuck on a particular problem. Sometimes a fresh perspective can make all the difference.

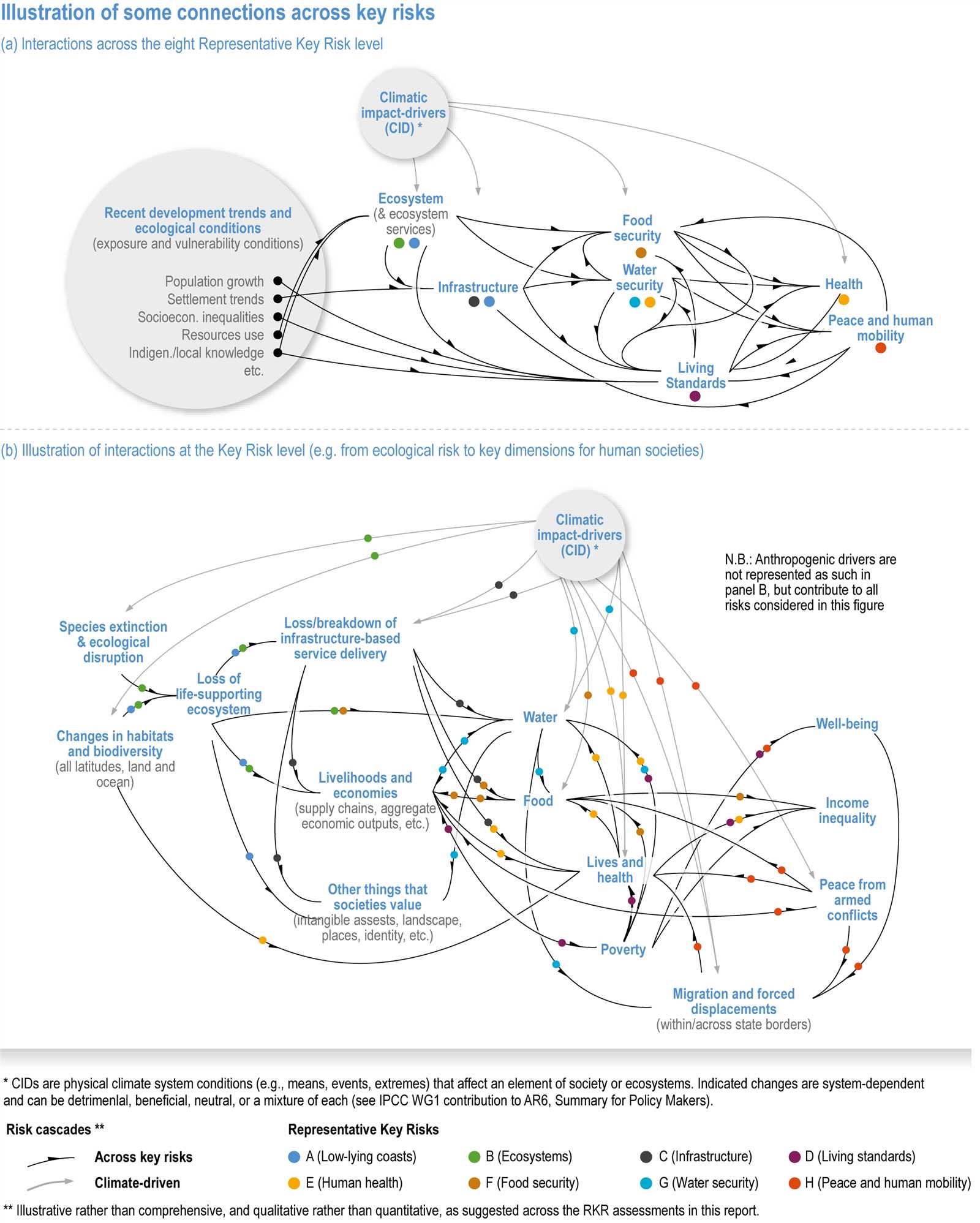
How to Approach Algebraic Equations

Approaching mathematical equations requires a systematic method to simplify and solve them effectively. Understanding the structure of an equation and recognizing the relationships between its components is essential for finding the solution. In this section, we will explore strategies for breaking down and solving various types of equations step by step.

Successful problem-solving begins with identifying the key elements of an equation, such as variables, constants, and operators. From there, it is important to apply logical steps to isolate the variable and simplify the equation. By following a clear and structured approach, even complex equations can be solved with ease.

Step-by-Step Approach

To solve an equation effectively, follow these general steps:

• Understand the equation: Carefully read through the equation to identify the components (variables, constants, coefficients, etc.).
• Isolate the variable: Start by getting the variable on one side of the equation. This can be done by adding, subtracting, multiplying, or dividing both sides of the equation.
• Simplify the equation: Combine like terms and perform operations that will simplify the equation as much as possible.
• Perform inverse operations: Use inverse operations to undo any actions applied to the variable (e.g., if the variable is multiplied by a number, divide both sides by that number).
• Check your solution: Once you’ve solved for the variable, substitute your solution back into the original equation to ensure it is correct.

Additional Tips for Success

Here are some additional tips to make solving equations more manageable:

1. Work methodically: Take your time to understand each step before moving forward. Rushing can lead to mistakes.
2. Practice regularly: The more equations you solve, the more comfortable you’ll become with different techniques and strategies.
3. Stay organized: Write out each step clearly to avoid confusion and ensure you’re following the correct process.

Step-by-Step Solutions for Exercises

Solving mathematical problems efficiently requires a clear, step-by-step approach. Breaking down each exercise into manageable stages helps to simplify the process and ensures accuracy. This section will provide a detailed guide to solving common types of problems, demonstrating how to apply the right techniques at every stage of the solution.

The key to mastering problem-solving is practicing each step in a logical order. By following a systematic approach, you will develop the ability to tackle increasingly complex problems with confidence. The examples provided will illustrate how to methodically apply strategies to reach the correct solution, making it easier to solve similar exercises independently.

Example Problem Solutions

Below is an example showing the step-by-step process for solving a typical problem:

Step	Action	Result
1	Write down the equation	x + 5 = 12
2	Subtract 5 from both sides	x = 7
3	Verify the solution by substituting x = 7	7 + 5 = 12, correct

This step-by-step process ensures clarity and avoids mistakes. Whether you’re solving linear equations or more complex expressions, following a structured approach will make problem-solving more manageable and accurate.

Breaking Down Complex Algebra Problems

When faced with intricate mathematical problems, it’s crucial to break them down into smaller, more manageable parts. By decomposing a complex problem into simpler components, you can solve each part step by step, which leads to a more straightforward and accurate solution. This approach not only makes the process more efficient but also helps in understanding the underlying principles that drive the solution.

The key to success in tackling complex problems lies in recognizing patterns, isolating variables, and applying appropriate operations to simplify the expression. Each problem can be approached methodically, ensuring that no detail is overlooked. As you break down a problem, consider using techniques like grouping like terms, applying the distributive property, or utilizing inverse operations to make the process smoother and more intuitive.

By following this structured approach, even the most challenging problems can be solved logically and efficiently. With practice, these techniques will become second nature, making complex problems much easier to navigate and understand.

Common Mistakes in Algebra

While solving mathematical problems, it’s easy to make mistakes that can throw off the entire solution. These errors often stem from misunderstandings of concepts or small miscalculations that, if not caught early, can lead to incorrect results. Recognizing common mistakes is crucial for improving problem-solving skills and ensuring accuracy.

One frequent error is overlooking the order of operations, which can lead to misinterpretations of an equation. Another common mistake involves failing to correctly simplify terms or distribute values properly, which may cause confusion during more complex steps. Carefully reviewing each step can help prevent these issues and ensure the final solution is correct.

Other errors might include misplacing negative signs, incorrectly combining like terms, or forgetting to check the solution. By staying organized and mindful of these typical mistakes, learners can improve their problem-solving approach and achieve more accurate results with each exercise.

Avoiding Errors in Chapter 2

When solving mathematical problems, it’s essential to stay attentive to detail in order to avoid common mistakes that can lead to incorrect results. These errors often arise from simple oversights, misunderstandings, or miscalculations that, if not caught early, can derail the entire process. To ensure accuracy and efficiency, it’s crucial to be aware of potential pitfalls and take steps to minimize them.

Key Strategies for Error Prevention

Several strategies can help you avoid mistakes and ensure accurate solutions:

• Follow the order of operations carefully: Always ensure that you’re performing mathematical operations in the correct sequence, starting with parentheses, exponents, multiplication and division, and finishing with addition and subtraction.
• Double-check your work: After completing each step, take a moment to review your calculations and make sure all terms have been correctly simplified and that no signs were overlooked.
• Understand the rules: Be sure you understand the rules of operations, such as distributing terms properly and handling negative signs accurately.

Common Mistakes to Watch Out For

Even experienced learners can make occasional errors. Here are some common mistakes to avoid:

• Overlooking negative signs: A small sign error can lead to an incorrect solution, so be careful when dealing with subtraction or negative numbers.
• Misapplying properties: Ensure that you are using the distributive and associative properties correctly when simplifying expressions.
• Skipping steps: Rushing through problems without fully working through each stage can result in missed details, leading to mistakes in the final answer.

By being mindful of these strategies and staying focused on the task at hand, you can minimize errors and improve your problem-solving accuracy in future exercises.

Tips for Mastering Algebra Skills

Mastering mathematical skills requires consistent practice and a deep understanding of fundamental concepts. By developing a strong foundation and applying effective strategies, you can tackle increasingly complex problems with confidence. This section outlines practical tips to help you strengthen your skills and improve your problem-solving abilities.

Success in mathematics is built on practice and persistence. The more problems you solve, the better you will become at recognizing patterns, applying formulas, and simplifying expressions. Below are several helpful tips to guide you through this process and make mastering the subject easier.

Effective Strategies for Improvement

• Practice regularly: The more problems you solve, the more familiar you’ll become with different techniques and strategies. Make solving math problems a daily habit to build confidence and fluency.
• Review core concepts: Ensure you have a solid grasp of the fundamental principles before moving on to more complex topics. Revisiting basic concepts will make learning advanced topics much easier.
• Work through examples: Studying solved examples helps you understand the step-by-step process and see how each technique is applied in context.

Additional Tips for Success

1. Stay organized: Break down problems into smaller, more manageable steps to avoid feeling overwhelmed. Keep your work neat and orderly to easily track your progress.
2. Don’t rush: Take your time with each problem. Rushing through solutions can lead to mistakes, especially with complex problems.
3. Seek help when needed: If you’re struggling with a concept, don’t hesitate to ask for clarification. Working with a tutor or studying with peers can help reinforce your understanding.

By following these tips and continuously applying yourself, you will steadily improve your skills and be able to solve even the most challenging problems with ease.

Effective Study Techniques for Algebra

To excel in solving mathematical problems, effective study techniques are crucial. Developing strong study habits not only improves understanding but also helps retain knowledge for future challenges. By approaching the subject with a well-structured plan, you can make learning more manageable and boost your confidence in tackling problems.

Studying mathematics requires both consistency and strategy. Focusing on key concepts, practicing regularly, and reviewing past work can significantly enhance your problem-solving skills. Below are several study techniques designed to optimize your learning experience and help you master essential skills.

Active Learning Strategies

Active learning encourages engagement with the material, which promotes better understanding and retention:

• Practice with purpose: Work through problems methodically, ensuring you understand each step. The more problems you solve, the more patterns and methods you’ll recognize.
• Teach what you’ve learned: Explaining concepts to someone else forces you to clarify your understanding and reinforces your own knowledge.
• Use a variety of resources: Supplement textbook problems with online tutorials, practice exercises, or video lessons to gain different perspectives on the material.

Time Management and Focus

Effective time management and concentration are vital for success:

• Break study sessions into intervals: Work in short bursts with breaks in between. This method, often called the Pomodoro Technique, helps maintain focus and reduces fatigue.
• Set achievable goals: Break down your study material into smaller sections and set clear, achievable goals for each session.
• Eliminate distractions: Create a quiet study environment free from distractions to ensure full focus during study time.

By incorporating these study techniques into your routine, you can enhance your learning experience, increase retention, and ultimately improve your ability to solve complex problems with confidence.

Real-World Applications of Algebra

Mathematics plays an essential role in many aspects of daily life, from simple tasks like budgeting to complex fields such as engineering and technology. The principles of solving equations and working with variables are not only theoretical but are applied in various real-world scenarios. Understanding how these skills are used outside the classroom can deepen your appreciation for their value and functionality.

In real-life situations, mathematical models help solve problems and make informed decisions. Whether it’s determining the optimal dimensions for a product, predicting future trends, or managing resources efficiently, the ability to work with equations is a powerful tool. Below are some of the many fields where these concepts are used daily.

Technology and Engineering

In the fields of technology and engineering, solving equations is crucial for designing and building new products, systems, and structures. Engineers rely on mathematical principles to:

• Design software: Programmers use algorithms, which often involve variables and functions, to develop applications and systems that perform specific tasks.
• Optimize structures: Engineers use equations to calculate the dimensions and materials needed for buildings, bridges, and machinery, ensuring they are both functional and safe.

Finance and Economics

Mathematics is also at the heart of finance and economics. It is used to:

• Calculate interest rates: Financial analysts use equations to determine how investments grow over time, factoring in rates of return, compound interest, and inflation.
• Budgeting and forecasting: Businesses and individuals apply mathematical models to predict future earnings, expenses, and investment returns.

As these examples show, the ability to work with equations is far from just an academic skill. It is a vital part of problem-solving and decision-making in the real world, affecting industries ranging from technology to economics and beyond.

Using Algebra in Everyday Life

Mathematical reasoning isn’t just for the classroom or specialized professions; it plays an essential role in many daily activities. Whether shopping for groceries, managing time, or making a home improvement project, mathematical principles help us make decisions and solve problems effectively. The ability to understand and apply these concepts enables better planning, organization, and optimization in everyday tasks.

By using variables and equations, we can approach a variety of real-life situations logically and with confidence. The following examples demonstrate how these skills come into play in common activities.

Personal Finance and Budgeting

One of the most practical applications of mathematical concepts is in personal finance. Whether it’s tracking expenses, planning for a trip, or saving for future goals, solving equations helps keep finances organized. For example, determining how much money you can save each month or predicting how long it will take to reach a savings goal involves basic arithmetic and problem-solving skills.

Expense	Cost	Total Savings Goal
Rent	$1,000	$5,000
Groceries	$300
Savings per month	$200

Home Improvement Projects

When undertaking a DIY project at home, mathematical skills help ensure accuracy. Whether measuring materials for a new piece of furniture or calculating the amount of paint needed for a room, solving problems related to dimensions, area, and volume is necessary. By using variables to represent unknown quantities, homeowners can make informed decisions about how much of each material to purchase, and how to use it efficiently.

In everyday life, problem-solving abilities allow us to approach tasks with greater efficiency and precision, saving time, effort, and resources.

Interactive Learning for Algebra

Incorporating interactive methods into education has proven to be highly effective in enhancing understanding and engagement. This approach allows learners to actively participate in the learning process rather than just passively receiving information. Interactive tools, such as online games, simulations, and real-time problem-solving exercises, enable students to experiment with concepts and receive immediate feedback, making learning more dynamic and engaging.

By using hands-on techniques, students can reinforce their understanding, correct mistakes, and solidify key principles. Interactive learning not only makes complex topics more accessible but also encourages curiosity and independent thinking. Here are some common interactive methods that can help boost learning:

• Interactive Simulations: Platforms that allow students to manipulate variables and observe outcomes in real time help to visualize abstract concepts.
• Online Problem Solvers: Websites and apps that offer step-by-step guidance help learners work through problems and instantly correct errors, building confidence along the way.
• Collaborative Learning: Group activities and peer discussions help students explain concepts to each other, reinforcing their own understanding and promoting teamwork.

These interactive learning methods encourage active involvement, making learning more personalized and effective. By using these tools, students can explore concepts at their own pace, reinforcing their skills and gaining a deeper understanding of the subject.

Online Resources for Algebra Students

The digital age has brought a wealth of educational tools and platforms that support learners in mastering complex subjects. For students looking to strengthen their understanding of mathematical concepts, online resources provide a variety of interactive lessons, tutorials, and practice problems. These platforms allow learners to study at their own pace and revisit difficult topics, helping them to build confidence and skill.

Here are some valuable online resources that can assist students in mastering key mathematical principles:

• Khan Academy: Offers free video lessons and practice exercises covering a wide range of topics, from basic equations to advanced problem-solving techniques.
• Wolfram Alpha: A powerful computational engine that helps students solve equations step by step, providing explanations and alternative solutions.
• IXL: A personalized learning platform that adapts to the learner’s level, offering practice problems and immediate feedback to help students improve their skills.
• PatrickJMT: Provides clear, concise math tutorials and examples, with a focus on helping students understand the steps involved in solving various problems.
• Desmos: An online graphing calculator that allows students to explore equations visually, making abstract concepts easier to understand.

Using these resources, students can access a wide range of materials tailored to different learning styles, helping them overcome challenges and excel in their studies. Whether through video tutorials, step-by-step problem solving, or interactive exercises, online tools make complex concepts more approachable and engaging.

Advanced Concepts in Chapter 2

As students progress in their studies, they are introduced to more intricate and abstract concepts that build upon foundational knowledge. These advanced ideas challenge learners to think critically and apply their understanding in more complex scenarios. In this section, we explore some of the key topics that form the core of advanced mathematical thinking, providing the necessary tools for solving sophisticated problems.

The following concepts represent the higher-level skills that students are expected to master:

• Systems of Equations: Understanding how to solve multiple equations simultaneously, finding common solutions, and interpreting the results in various contexts.
• Quadratic Functions: Delving into the properties and graphs of quadratic equations, including solving for unknowns and analyzing the vertex form.
• Exponents and Logarithms: Mastering the rules of exponents, and learning how to apply logarithmic functions to solve equations involving large or small numbers.
• Polynomials and Factoring: Exploring how to factor complex polynomial expressions and solve problems using different factoring techniques.
• Rational Expressions: Simplifying, multiplying, dividing, and solving equations with rational expressions, as well as understanding how to handle restrictions on variables.

These advanced topics form the foundation for solving more complicated mathematical problems, and mastering them is essential for success in higher-level courses. By strengthening their skills in these areas, students are able to approach challenging questions with greater confidence and clarity.

Exploring Complex Algebraic Ideas

As learners delve deeper into mathematical theory, they encounter more intricate and sophisticated concepts that push the boundaries of their understanding. These advanced ideas often involve abstract thinking, challenging students to apply their foundational knowledge in new and innovative ways. Exploring these concepts not only strengthens problem-solving skills but also helps to develop a deeper appreciation for the elegance of mathematics.

One of the most important areas of focus at this stage is understanding how to manipulate and work with expressions and equations that appear increasingly complex. Below, we explore some of the key topics that are essential for mastering these advanced mathematical challenges.

Working with Systems of Equations

Solving systems of equations is a crucial skill for handling multiple unknowns. At this level, students learn to apply different methods such as substitution, elimination, and matrix operations to find the solution set. These systems can be linear, nonlinear, or a combination of both, requiring different strategies and approaches depending on the situation.

Understanding Polynomial Expressions

Polynomials, which involve terms with varying powers of variables, are foundational to higher-level mathematics. In this section, students are tasked with factoring, expanding, and simplifying polynomial expressions. This includes working with special forms like the difference of squares, perfect square trinomials, and cubic equations. Mastery of these techniques is vital for solving more complex equations and understanding the behavior of polynomials in different contexts.

As students continue to explore these challenging topics, they gain the skills necessary to solve a broad range of complex problems, laying the groundwork for further study in advanced mathematics.

​

Improving Your Algebra Skills

Mastering mathematical concepts requires consistent practice and a deep understanding of the underlying principles. By strengthening your approach to problem-solving, you can enhance your proficiency in solving equations and tackling complex tasks with greater ease. In this section, we’ll explore strategies that can help you build a solid foundation and improve your mathematical thinking.

Effective Strategies for Mastery

To improve your skills, it is important to develop effective strategies that focus on both understanding and practice. These approaches include:

• Breaking down problems into smaller, manageable parts.
• Using different methods to solve the same problem for better insight.
• Practicing regularly to build muscle memory and speed.
• Seeking help when stuck and collaborating with others.

Focus Areas for Growth

To make significant progress, it is helpful to focus on key areas of study that often present challenges. These include:

1. Identifying patterns and understanding relationships between numbers.
2. Working with variables and simplifying expressions.
3. Learning how to manipulate and solve equations accurately.
4. Understanding functions and how they apply to real-world scenarios.

By honing in on these areas and practicing regularly, you’ll see gradual improvement and gain more confidence in your problem-solving abilities.