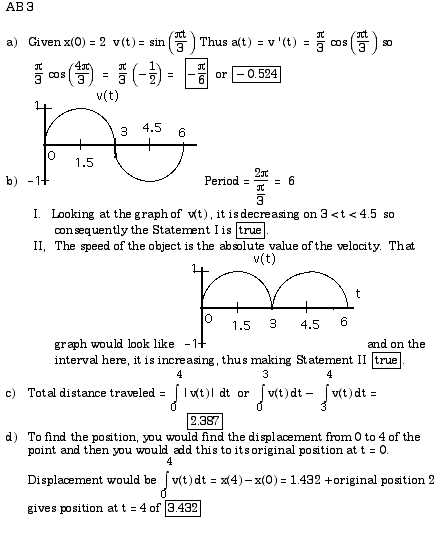
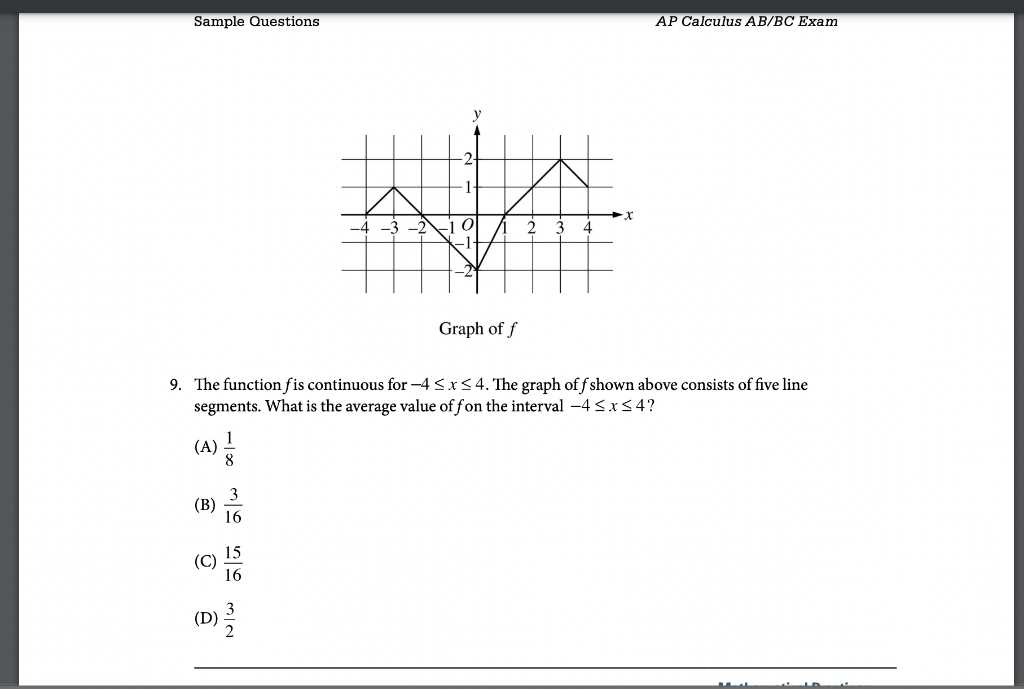
AP Calculus AB Sample Exam Questions for Practice

Preparing for advanced mathematics assessments requires a focused approach to mastering core concepts. In this section, we explore key areas of focus that will help strengthen your understanding and improve your performance. Whether you’re reviewing specific problems or tackling complex challenges, this resource will guide you through the essential steps needed to succeed.

Familiarity with the format is crucial for effective preparation. By working through various types of problems, you’ll become more confident in identifying patterns and applying the right methods. This will not only enhance your problem-solving abilities but also allow you to manage time efficiently during the actual assessment.

Through targeted practice, you can refine techniques for solving mathematical problems. The exercises here cover a wide range of topics, from basic principles to advanced applications. Engaging with these examples will allow you to strengthen key skills and identify areas for further review.

AP Calculus AB Practice Problems

Effective preparation for advanced mathematics assessments requires consistent practice with a variety of challenges. Working through problems designed to cover key concepts is an essential part of strengthening your understanding. This section provides carefully crafted exercises that mirror the format and difficulty level you can expect in the actual test.

Types of Problems to Focus On

These exercises range from fundamental to complex scenarios, each requiring a different approach. Emphasis is placed on understanding core principles such as limits, derivatives, and integrals. By practicing these, you’ll develop the ability to analyze and solve problems more efficiently.

Applying Techniques to Real-World Problems

The best way to grasp mathematical concepts is through real-world applications. Many of the problems in this section are rooted in practical situations where abstract theories are applied to solve tangible issues. Working through these examples will help you connect theory to practice and build confidence in your problem-solving abilities.

Overview of AP Calculus AB Exam

The AP assessment in advanced mathematics is designed to evaluate your understanding of key mathematical concepts and problem-solving skills. This test covers a wide range of topics that are fundamental to higher-level mathematics and sciences, providing an opportunity to showcase your ability to apply theoretical knowledge to complex problems.

Structure of the Assessment

The assessment is divided into two main sections: multiple-choice and free-response. The multiple-choice portion tests your ability to quickly analyze and solve problems, while the free-response section allows for a more in-depth demonstration of your understanding through detailed solutions and explanations.

Key Areas of Focus

Throughout the test, you will encounter problems related to differentiation, integration, limits, and series. It is essential to be familiar with each of these areas, as they form the foundation of many real-world applications. Mastery of these concepts will ensure that you can approach each question with confidence and accuracy.

Key Topics Covered in AP Calculus AB

The assessment focuses on a wide range of fundamental mathematical concepts that are essential for understanding advanced problem-solving techniques. Below are some of the key areas you’ll encounter, each critical to mastering the subject and performing well in the assessment.

• Limits and Continuity: Understanding the behavior of functions as they approach specific points and the concept of continuity.
• Derivatives: Techniques for finding the rate of change of functions and their applications in real-world problems.
• Applications of Derivatives: Using the derivative to solve problems involving motion, optimization, and related rates.
• Integrals: Methods for finding the area under curves and solving problems involving accumulation and area.
• Fundamental Theorem of Calculus: Connecting differentiation and integration to solve problems more effectively.
• Series: Working with sequences and series, including convergence tests and Taylor expansions.

Familiarizing yourself with these topics and practicing problems in each area will ensure you’re well-prepared to tackle the challenges of the test. Mastery of these concepts is crucial for success in both the assessment and future studies in related fields.

How to Approach AP Exam Questions

When tackling advanced mathematics assessments, it’s essential to have a clear strategy to ensure accuracy and efficiency. Approaching each problem with a structured method will help you identify the most effective solutions while managing your time effectively. Below are some key strategies to keep in mind as you work through the problems.

• Read Carefully: Ensure you understand the problem completely before beginning to solve it. Pay attention to any specific instructions or constraints given in the prompt.
• Identify Key Information: Highlight or underline important values, variables, and conditions that will guide your solution process.
• Break Down the Problem: If the problem seems complex, break it down into smaller, more manageable steps. Solve each part sequentially.
• Use the Appropriate Techniques: Recognize which mathematical tools or formulas are needed to address the specific type of problem. This will save time and reduce errors.
• Check Your Work: After solving a problem, quickly review your steps to ensure no mistakes were made, especially with calculations and logic.

By staying focused and organized, you can approach each challenge confidently, making the most of the time allotted and boosting your chances of success.

Practice Problems for Differentiation

Mastering the process of finding rates of change is fundamental to solving many advanced mathematical problems. This section provides a variety of practice problems that focus on differentiation techniques, helping you gain confidence in applying rules and solving real-world scenarios. By working through these exercises, you’ll enhance your ability to approach problems involving slopes, tangents, and rates of change.

These problems cover a wide range of functions, including polynomials, trigonometric expressions, and exponential functions. They will challenge you to use different rules, such as the power rule, product rule, quotient rule, and chain rule, to find derivatives efficiently.

As you work through the exercises, focus on simplifying expressions step-by-step and ensuring that you understand each transformation. This will not only improve your problem-solving skills but also prepare you for more complex applications in future challenges.

Understanding Integration Techniques

Integration is a fundamental process that allows you to find the accumulated quantity over a specific interval, whether it’s the area under a curve or the total accumulation of a rate. In this section, we’ll explore various methods used to solve integration problems, helping you to tackle a broad range of challenges effectively.

Basic Methods of Integration

The most common technique for integration is the antiderivative, which involves reversing the process of differentiation. Understanding how to find the antiderivative of basic functions such as polynomials, exponentials, and trigonometric expressions is essential. You will also need to be familiar with common integral rules like the constant multiple rule and the power rule for integration.

Advanced Integration Techniques

In more complex scenarios, additional techniques are needed to solve integrals that cannot be directly addressed by basic methods. These include integration by parts, trigonometric substitution, and partial fractions. Each of these methods allows you to break down complex integrals into simpler parts, making them easier to solve. Mastery of these advanced techniques is key for solving more difficult problems.

Through consistent practice and application of these techniques, you’ll build the skills necessary to solve integration problems efficiently and accurately.

Limits and Continuity Practice Questions

Understanding the behavior of functions as they approach specific points is essential in solving many mathematical problems. This section focuses on exercises designed to strengthen your grasp of the concepts of limits and continuity. By working through these problems, you’ll enhance your ability to analyze functions and determine their behavior under various conditions.

Evaluating Limits

When approaching limits, it is important to understand how a function behaves as it nears a particular value. This practice will help you apply techniques like direct substitution, factoring, and L’Hopital’s Rule to determine the limit of different functions. Below is a table summarizing some common methods for evaluating limits:

Method	Description	Example
Direct Substitution	Substitute the value of x directly into the function, provided the function is continuous at that point.	limx→2 (x² – 4) = 0
Factoring	Factor the function to simplify it and then substitute the value of x.	limx→3 (x² – 9)/(x – 3) = 6
L’Hopital’s Rule	Used for indeterminate forms like 0/0. Differentiate the numerator and denominator separately, then re-evaluate the limit.	limx→0 sin(x)/x = 1

Continuity of Functions

For a function to be continuous at a point, it must meet three conditions: it must be defined at that point, the limit must exist, and the limit must equal the function’s value at that point. Understanding these criteria is crucial for solving problems involving discontinuities and ensuring functions behave as expected. Below are a few examples of types of discontinuities:

• Removable Discontinuities: Occur when a function is not defined at a point but can be made continuous by filling in a single value.
• Jump Discontinuities: Occur when a function suddenly jumps from one value to another at a certain point.
• Infinite Discontinuities: Occur when a function approaches infinity at a particular point.

Practice solving problems involving these concepts to strengthen your ability to assess the limits and continuity of various functions.

Analysis of Derivative Word Problems

Word problems involving rates of change often require you to interpret real-world scenarios using mathematical principles. In this section, we’ll explore how to approach and solve problems that involve finding the rate of change of a quantity with respect to another. These types of problems can appear in various contexts, such as motion, growth, or optimization, and they typically require translating the information given into mathematical expressions before solving.

To successfully solve these problems, it’s essential to break the problem into smaller, manageable steps. Start by identifying the variables involved, then write down any equations or relationships that connect them. Next, use the derivative to determine the rate of change, paying careful attention to any units and interpreting the results in the context of the problem.

By practicing these types of problems, you’ll become more comfortable with applying differentiation to real-world situations, improving both your problem-solving skills and your understanding of how rates of change are used in various fields.

Exam Strategy for Related Rates

Related rates problems often require you to analyze how different quantities change over time and are linked through a common variable. These problems can be tricky, as they typically involve multiple variables and require you to differentiate implicitly. Having a solid strategy for approaching these types of problems will help you solve them accurately and efficiently during a time-constrained assessment.

Step-by-Step Approach

When tackling a related rates problem, follow these essential steps to ensure clarity and correctness in your solution:

• Identify the variables: Determine all the quantities that are changing and assign variables to each of them.
• Write down the equation: Find a relationship between the variables. This could be a geometric formula or a more general equation that relates the quantities.
• Differentiate with respect to time: Use implicit differentiation to find the derivatives of the equation. Be sure to apply the chain rule where necessary.
• Substitute known values: Plug in the given values for the variables and their rates of change. Solve for the unknown rate.

Practice Common Types of Problems

Familiarizing yourself with typical related rates problems will help you recognize common patterns. Some common scenarios include problems involving the rates of change of distances, areas, volumes, or even more abstract quantities. By practicing these problems, you’ll be able to quickly identify the key steps and avoid unnecessary mistakes when time is limited.

Incorporating this approach into your preparation will not only increase your efficiency but also help you feel confident when working through related rates problems in assessments.

Application of Mean Value Theorem

The Mean Value Theorem (MVT) is a powerful concept that connects the behavior of a function on an interval to the behavior of its derivative at a specific point. In essence, the theorem guarantees that under certain conditions, there is at least one point where the instantaneous rate of change equals the average rate of change over the interval. Understanding how to apply this theorem can help solve problems related to rates of change, motion, and optimization.

To effectively use the Mean Value Theorem, first ensure that the function meets the necessary conditions: it must be continuous on the closed interval and differentiable on the open interval. Once these conditions are satisfied, the theorem provides a means to find specific information about the function’s behavior, even if you don’t have the exact equation or value at a particular point.

In practical terms, the MVT can be used to estimate velocities in motion problems, verify function behavior, or prove the existence of certain points where certain conditions are met. By applying this theorem, you can gain insights into the function’s dynamics and make more informed conclusions about its overall behavior.

Sample Questions on Optimization

Optimization problems are essential in understanding how to find maximum or minimum values for various quantities, such as cost, area, or volume, in real-world situations. These problems often require you to find the optimal values that satisfy a given set of conditions. This section provides practice exercises that involve maximizing or minimizing certain functions, which are critical in fields like economics, physics, and engineering.

Problem 1: Maximizing Area

Consider a problem where you are tasked with finding the largest possible area of a rectangle inscribed within a circle of fixed radius. The goal is to determine the dimensions of the rectangle that will give the maximum area.

Problem 2: Minimizing Cost

In another scenario, you might be asked to minimize the cost of materials used to construct a box with a fixed volume. The task is to determine the dimensions of the box that will result in the least cost, given the price per square unit of surface area.

Optimization Problem Summary

Below is a summary of some common types of optimization problems that you might encounter. The table provides examples of problems and the approach to solving them:

Type of Problem	Description	Approach
Maximizing Area	Find the maximum area of a geometric figure under certain constraints.	Use derivative techniques to find critical points, then verify maxima or minima.
Minimizing Cost	Minimize the cost of materials given volume or surface area constraints.	Express the cost function, take the derivative, and find the minimum value.
Maximizing Revenue	Optimize revenue given price and quantity constraints.	Set up the revenue function, differentiate, and solve for the maximum.

By working through these optimization problems, you will develop a deeper understanding of how to use derivatives to solve real-world optimization scenarios effectively.

Integration by Parts Practice Problems

Integration by parts is a technique used to integrate the product of two functions. It is based on the product rule of differentiation and is particularly useful when one of the functions becomes simpler after differentiation. This method can be applied to a wide range of problems, especially when dealing with products of polynomials, exponentials, and trigonometric functions. Practicing this technique helps build confidence in solving more complex integrals.

Problem 1: Polynomial and Exponential Function

Integrate the following expression:

• ∫ x e^x dx

Solution: Choose u = x and dv = e^x dx, then proceed with the integration by parts formula.

Problem 2: Trigonometric and Exponential Functions

Integrate the following expression:

• ∫ e^x sin(x) dx

Solution: Use integration by parts twice, each time simplifying the result to eventually solve the integral.

Problem 3: Logarithmic and Polynomial Function

Integrate the following expression:

• ∫ ln(x) dx

Solution: Use integration by parts by letting u = ln(x) and dv = dx. This problem helps understand how logarithmic functions interact with integration techniques.

Additional Practice

For further practice, here are a few more integrals to solve using integration by parts:

• ∫ x cos(x) dx
• ∫ ln(x) e^x dx
• ∫ x^2 e^(-x) dx

These problems reinforce the application of the integration by parts technique and provide a solid foundation for tackling more challenging integrals. Regular practice will make this method more intuitive and easier to apply in various contexts.

Antiderivatives and Area Under Curve

Antiderivatives and the area under a curve are fundamental concepts in integral analysis. The process of finding an antiderivative involves determining the original function from its rate of change, while the area under a curve represents the accumulation of quantities over a given interval. These two ideas are closely related, as the area under a curve can often be computed using antiderivatives, particularly when dealing with definite integrals. Understanding both concepts is crucial for solving a wide range of problems in mathematics and applied fields.

Antiderivatives and Their Significance

An antiderivative is essentially the reverse process of differentiation. If a function has a known derivative, the antiderivative helps us recover the original function. In practical terms, this is useful for finding the accumulated total of a quantity, such as distance traveled over time or the total amount of material used in a project.

Finding the Area Under a Curve

To calculate the area under a curve between two points, we use the concept of integration. The integral of a function over an interval gives us the total accumulated area between the curve and the x-axis. This can be particularly useful when the exact value of the area is not easily calculated through geometric methods.

Practice Problems

Below are some common problems involving antiderivatives and area under the curve. These problems provide valuable practice for mastering these key concepts:

Problem	Antiderivative	Area Under Curve (Definite Integral)
∫ 3x^2 dx	Antiderivative: x^3 + C	Area: ∫ from 1 to 2 of 3x^2 dx = [x^3] from 1 to 2 = 8 – 1 = 7
∫ e^x dx	Antiderivative: e^x + C	Area: ∫ from 0 to 1 of e^x dx = [e^x] from 0 to 1 = e – 1 ≈ 1.718
∫ sin(x) dx	Antiderivative: -cos(x) + C	Area: ∫ from 0 to π of sin(x) dx = [ -cos(x) ] from 0 to π = 2

By solving these problems and applying the concept of antiderivatives, you will gain a deeper understanding of how to calculate the total area under a curve, which is a critical skill in a variety of mathematical and real-world applications.

Fundamental Theorem of Calculus Explained

The fundamental theorem is a key concept in mathematical analysis that establishes a direct connection between two core operations: finding the area under a curve and determining the rate of change of a function. This theorem bridges the gap between differentiation and integration, providing a way to evaluate the total accumulation of a function’s values over a specified interval. Understanding its two main parts is essential for solving complex problems in various fields of mathematics and science.

The First Part: Relationship Between Derivatives and Integrals

The first part of the theorem states that if a function is continuous over an interval, the integral of its derivative over that interval equals the difference between the function’s values at the endpoints. In simpler terms, it tells us that the process of finding an antiderivative (integral) and differentiating a function are inverses of each other.

• If ( f ) is a continuous function on an interval ( [a, b] ), and ( F ) is an antiderivative of ( f ), then:
• ( int_a^b f(x) , dx = F(b) – F(a) )

This means that to compute the area under the curve of ( f(x) ) from ( a ) to ( b ), we simply find an antiderivative of ( f(x) ) and evaluate it at the limits of integration. This part of the theorem allows for easy calculation of definite integrals.

The Second Part: Using Integrals to Find Derivatives

The second part of the fundamental theorem provides a way to find the derivative of an integral function. It tells us that if we define a function as the integral of another function over an interval that depends on the variable, we can differentiate that function with respect to the variable. This is particularly useful in problems involving changing limits of integration.

• If ( f ) is continuous on ( [a, x] ), and ( F(x) = int_a^x f(t) , dt ), then:
• ( F'(x) = f(x) )

Thus, by applying this part of the theorem, we can differentiate integral expressions, which simplifies the process of solving many real-world problems involving accumulation and rates of change.

By grasping both parts of the fundamental theorem, you gain a powerful tool for working with integrals and derivatives, which are central to understanding dynamic systems and modeling real-world phenomena.

Practice Questions on Differential Equations

In this section, we will explore problems involving rates of change and their applications. These types of mathematical models describe how quantities evolve over time or space. Solving these equations is key to understanding how systems behave in areas such as physics, biology, economics, and engineering. By practicing these problems, you will develop a deeper insight into the techniques used to analyze dynamic systems.

Example 1: Simple Growth Model

Consider a population of bacteria that grows at a rate proportional to its current size. If the rate of change of the population ( P ) is given by the equation:

( frac{dP}{dt} = kP ), where ( k ) is a constant, and ( P(0) = 100 ), find the general solution for ( P(t) ). How would the population behave as time progresses?

• Hint: This is a separable equation. Integrate both sides to find the solution.

Example 2: Radioactive Decay

A sample of a radioactive substance decays at a rate proportional to the amount remaining. The rate of decay is given by the equation:

( frac{dN}{dt} = -lambda N ), where ( lambda ) is a constant and ( N(t) ) represents the amount of substance at time ( t ). Given that the initial amount is ( N(0) = 500 ), determine the quantity ( N(t) ) at any time ( t ).

• Hint: Use separation of variables and apply the initial condition to solve for the constant of integration.

These problems demonstrate fundamental techniques for solving differential equations, such as separation of variables and applying initial conditions to find specific solutions. Mastery of these methods is crucial for addressing a wide range of real-world scenarios where change is continuous and dependent on the system’s current state.

Preparing for Multiple Choice Section

The multiple-choice portion of the assessment tests your ability to apply key concepts efficiently and accurately under time constraints. Each problem requires a quick analysis, applying various techniques to arrive at the correct answer. Understanding the format, common types of problems, and the strategies to approach them will give you a significant advantage in managing time and reducing errors.

Common Types of Problems

Here are some typical categories you will encounter in the multiple-choice section:

Topic	Description
Rates of Change	Questions that involve solving for rates of change in various contexts, such as motion or population growth.
Area Under Curves	Questions that require the calculation of areas or total quantities represented by a curve, using integration concepts.
Optimization Problems	Problems that ask you to find the maximum or minimum values of functions based on real-world scenarios.
Function Behavior	Questions that ask for the analysis of limits, continuity, and the overall behavior of a function.

Strategic Tips for Success

To excel in this section, consider the following strategies:

• Read carefully: Understand exactly what the problem is asking before jumping to solve it.
• Identify key information: Quickly highlight given values or conditions that will guide your solution.
• Eliminate obvious wrong answers: Often, you can rule out one or two choices immediately based on logic.
• Use estimation when necessary: If you are unsure, approximating can sometimes lead to narrowing down choices.
• Manage your time: Keep an eye on the clock, but don’t rush–accuracy is more important than speed.

With practice and preparation, you’ll become more adept at quickly identifying the right approach for each problem, ensuring that you maximize your performance in this section.

Free Response Question Tips

The free-response section presents an opportunity to showcase your problem-solving skills in a more comprehensive and detailed manner. Unlike multiple-choice problems, these require you to construct solutions step by step, demonstrating not only the final answer but also the reasoning behind it. Having a clear strategy for approaching these types of problems can significantly boost your performance.

Approach with Confidence

To effectively tackle free-response items, consider these key strategies:

• Read the Problem Thoroughly: Start by carefully reading the prompt to ensure you understand the task at hand. Take note of key terms and conditions.
• Plan Your Solution: Before diving into calculations, outline your approach. Identify the concepts or formulas that might apply to the problem.
• Show Your Work: Clearly label each step of your solution. Presenting a logical progression not only ensures clarity but also maximizes the chances of receiving partial credit.
• Stay Organized: Keep your work neat and orderly. This helps prevent mistakes and makes it easier for graders to follow your reasoning.
• Check for Accuracy: Always review your work if time allows. Double-check calculations and ensure that you have answered all parts of the problem.

Common Pitfalls to Avoid

While working through these problems, keep an eye out for common mistakes:

• Skipping Units: Always include units where applicable. Failing to do so may cost you valuable points.
• Missing Intermediate Steps: Even if you can solve the problem mentally, it’s important to show each step for full credit.
• Ignoring Special Conditions: Make sure to address any constraints or special instructions mentioned in the prompt.
• Rushing: Avoid the temptation to rush through the solution. Take your time to ensure clarity and accuracy in your work.

By following these tips and practicing regularly, you’ll develop the confidence and expertise necessary to perform well in the free-response section. The key is not only solving the problem but demonstrating your understanding in a structured and thoughtful way.

Time Management During AP Exam

Effective time management is a crucial aspect of achieving success in any timed assessment. When faced with a series of problems under time constraints, it is essential to allocate your time wisely, balancing between speed and accuracy. A well-structured approach can help you remain calm, focused, and ensure that all sections are completed thoroughly.

Here are some strategies to optimize your time:

• Familiarize Yourself with the Format: Knowing the structure of the assessment beforehand allows you to plan accordingly. You will have a clear idea of how much time to dedicate to each section.
• Prioritize Easy Problems: Start by tackling the problems you find most manageable. This builds confidence and ensures you accumulate easy points early on.
• Set Time Limits: Set specific time limits for each section or problem. Use a watch or timer to monitor your progress, making sure you stay on track.
• Don’t Get Stuck: If a problem is taking too long, move on to the next one. It’s better to complete all problems than to spend excessive time on a single question.
• Allocate Time for Review: Always leave some time at the end for reviewing your work. This helps catch errors and verify your answers.

By implementing these time management techniques, you can enhance your efficiency and increase your chances of performing well. With practice, these strategies will become second nature, allowing you to approach the assessment with a clear and calm mindset.