E2025 Algebra 2 Semester 1 Answers

Mathematics can be challenging, especially when faced with complex problems that require a deep understanding of various principles. Whether you are revisiting familiar concepts or tackling new material, grasping the core ideas is essential for progress. This section will guide you through the key topics covered in the first part of a higher-level math course, offering practical solutions and insights to help you navigate through difficult problems.

Throughout this journey, you will encounter several important techniques, such as solving equations, graphing functions, and applying advanced problem-solving strategies. The goal is to provide clear explanations and effective methods to ensure you can approach each task with confidence and precision. By focusing on the fundamental concepts and practicing regularly, you’ll develop a solid foundation to excel in more advanced topics.

Whether you’re looking to improve your grades or deepen your understanding, this guide offers the support you need to succeed in mathematical studies.

Understanding E2025 Algebra 2 Curriculum

The curriculum for this level of mathematics focuses on building a strong foundation in advanced problem-solving techniques. It is designed to challenge students and enhance their critical thinking skills, providing them with the tools necessary to tackle increasingly complex topics. The material is structured to promote both understanding and application of mathematical principles in various contexts.

Throughout the course, students will explore a variety of mathematical concepts, including the manipulation of polynomials, functions, and equations. Emphasis is placed on both theoretical understanding and practical problem-solving strategies. By mastering these key topics, learners can successfully apply their knowledge in real-world situations, strengthening their analytical abilities and preparing them for further academic pursuits.

Success in this course requires a strong commitment to practice and a thorough understanding of the key concepts, which will be developed throughout the lessons.

Key Concepts Covered in Algebra 2

This stage of mathematics introduces several foundational ideas that will be essential for tackling higher-level topics. Students will encounter a wide range of techniques aimed at enhancing their ability to solve complex equations and understand abstract concepts. The focus will be on developing a deeper understanding of the relationships between variables and how to manipulate these relationships effectively in different mathematical contexts.

Understanding Functions and Graphing

One of the core concepts involves mastering functions and their graphs. Students will learn to recognize and interpret different types of functions, such as linear, quadratic, and exponential. Emphasis is placed on graphing techniques, allowing students to visualize relationships between variables and understand how changes in one variable affect the other. This visual approach helps solidify abstract concepts and aids in problem-solving.

Advanced Equation Solving Techniques

Another key area is the mastery of advanced equation solving. Students will delve into solving systems of equations, both algebraically and graphically. They will explore methods like substitution, elimination, and matrix operations. These techniques are fundamental for understanding how multiple variables interact and how to find solutions that satisfy all given conditions. The goal is to foster a robust problem-solving skill set that can be applied in a variety of scenarios.

Solving Equations in Algebra 2

At this level of mathematics, solving equations becomes more intricate as students encounter a variety of problem types that require advanced methods. Understanding the process of finding unknown values by manipulating equations is essential for success. The focus is on applying these methods to more complex equations, where the relationships between variables may not be immediately obvious. Mastery of these techniques ensures that students can approach even the most challenging problems with confidence.

Linear and Quadratic Equations

Linear and quadratic equations are fundamental building blocks in equation solving. Students will refine their skills in solving both types by employing techniques such as factoring, completing the square, and using the quadratic formula. These methods provide systematic ways to find solutions and are crucial for understanding how equations evolve as their complexity increases.

Systems of Equations

In addition to individual equations, solving systems of equations plays a significant role in this stage of mathematics. Students will learn to solve multiple equations that share common variables. Methods such as substitution, elimination, and graphing will be explored to find the intersection points of the equations, providing solutions that satisfy all conditions simultaneously.

Method	Description	Example
Substitution	One equation is solved for one variable and then substituted into the other equation.	x = 2, y = 3
Elimination	Adding or subtracting equations to eliminate one variable, allowing for easier solving.	x = 5, y = -1
Graphing	Graph both equations and find the point(s) where they intersect.	(3, 4)

Tips for Mastering Polynomial Functions

Polynomial functions are a key aspect of advanced mathematics, offering a wide range of applications and problem-solving opportunities. To succeed in working with these functions, it’s important to develop a clear understanding of their structure and behavior. By mastering essential techniques and strategies, students can confidently handle tasks that involve graphing, simplifying, and solving polynomial equations.

Start by becoming familiar with the basic terms and components, such as coefficients, exponents, and terms. Recognizing the general form of a polynomial will make it easier to identify its degree, leading to a better understanding of its behavior. Practice simplifying polynomials by combining like terms, and focus on mastering factoring techniques, which are essential for solving polynomial equations.

Additionally, understanding how to graph polynomial functions is crucial. Pay attention to key features such as intercepts, turning points, and end behavior. Graphing by hand can strengthen your understanding of how changes in the equation affect the graph’s shape, and using technology can further refine this skill. Through consistent practice and application, you’ll gain confidence in navigating polynomial problems with ease.

Exploring Rational Expressions and Equations

Rational expressions and equations are an essential part of advanced mathematics, requiring students to manipulate ratios of polynomials. Understanding how to simplify, solve, and perform operations on these expressions is critical for solving more complex problems. The focus is on identifying common factors, reducing fractions, and applying algebraic techniques to find solutions to equations involving rational functions.

Simplifying Rational Expressions

One of the first steps in working with rational expressions is simplification. This involves factoring both the numerator and the denominator to cancel out any common factors. Mastery of factoring techniques is essential for reducing expressions to their simplest form, making subsequent steps easier to handle.

Solving Rational Equations

Solving equations that involve rational expressions requires a careful approach. First, students must identify and eliminate any denominators, often by multiplying both sides of the equation by the least common denominator (LCD). Once the denominators are removed, the equation becomes simpler to solve, but it’s important to check for any extraneous solutions that may arise from the initial denominators.

Step	Explanation	Example
Factor both numerator and denominator	Identify common factors to simplify the expression.	(x^2 – 4)/(x^2 – 2x) simplifies to (x+2)/x
Multiply by LCD	Eliminate denominators by multiplying through by the least common denominator.	(1/x) + (2/x^2) = 3 simplifies by multiplying both sides by x^2.
Check for extraneous solutions	Verify that any solutions found don’t result in division by zero.	For x = 0, check if it causes a denominator to become zero.

How to Tackle Quadratic Equations

Quadratic equations are a cornerstone of advanced mathematics, and solving them requires a deep understanding of the methods and strategies involved. These types of equations are typically represented in a standard form, and there are various techniques to find their solutions. By mastering these methods, students can confidently approach problems that involve unknowns squared, making it easier to identify the roots of an equation.

Using the Quadratic Formula

The quadratic formula is one of the most reliable methods for solving any quadratic equation. It allows students to find solutions by substituting the coefficients of the equation into the formula: x = (-b ± √(b² – 4ac)) / 2a. This approach works for all types of quadratic equations, whether they have real or complex solutions. Understanding how to apply the formula efficiently is crucial for solving more difficult problems.

Factoring Quadratics

Factoring is another powerful technique for solving quadratic equations. When the quadratic equation is factorable, it can be expressed as a product of two binomials. By setting each factor equal to zero, students can quickly find the solutions. This method is often quicker than using the quadratic formula, but it requires practice in recognizing when an equation is factorable.

Graphing Techniques for Algebra 2

Graphing is an essential skill in advanced mathematics, helping students visualize relationships between variables. Whether dealing with linear, quadratic, or more complex functions, understanding graphing techniques is crucial for interpreting equations and solving problems. A clear grasp of how to plot and analyze graphs enables students to draw meaningful conclusions about the data and relationships they are studying.

Graphing Linear Functions

When graphing linear functions, students must identify key components such as the slope and the y-intercept. These two elements determine the line’s direction and where it crosses the y-axis. By using the slope-intercept form y = mx + b, students can easily plot the line by starting at the y-intercept and using the slope to determine additional points along the line.

• Identify the y-intercept (b) and plot it on the graph.
• Use the slope (m) to find the next points.
• Draw a straight line through the points to complete the graph.

Graphing Quadratic Functions

Quadratic functions often form parabolic curves. To graph these functions, students must recognize the equation’s key features, including the vertex and axis of symmetry. The vertex provides the highest or lowest point on the graph, depending on whether the parabola opens upward or downward. The axis of symmetry divides the parabola into two symmetrical halves, helping in plotting the curve accurately.

1. Identify the vertex, either from the vertex form or by using the formula for the x-coordinate of the vertex.
2. Plot additional points using symmetry around the axis of symmetry.
3. Draw the parabola, ensuring it opens in the correct direction.

Explaining Exponential and Logarithmic Functions

Exponential and logarithmic functions are closely related concepts that form the foundation for understanding a wide range of real-world phenomena. These functions often model growth and decay, making them crucial in fields such as finance, biology, and physics. While exponential functions involve rapid increases or decreases, logarithmic functions help reverse these processes, providing a way to solve equations involving exponents. Understanding their relationship and properties is essential for solving complex mathematical problems.

Exponential Functions

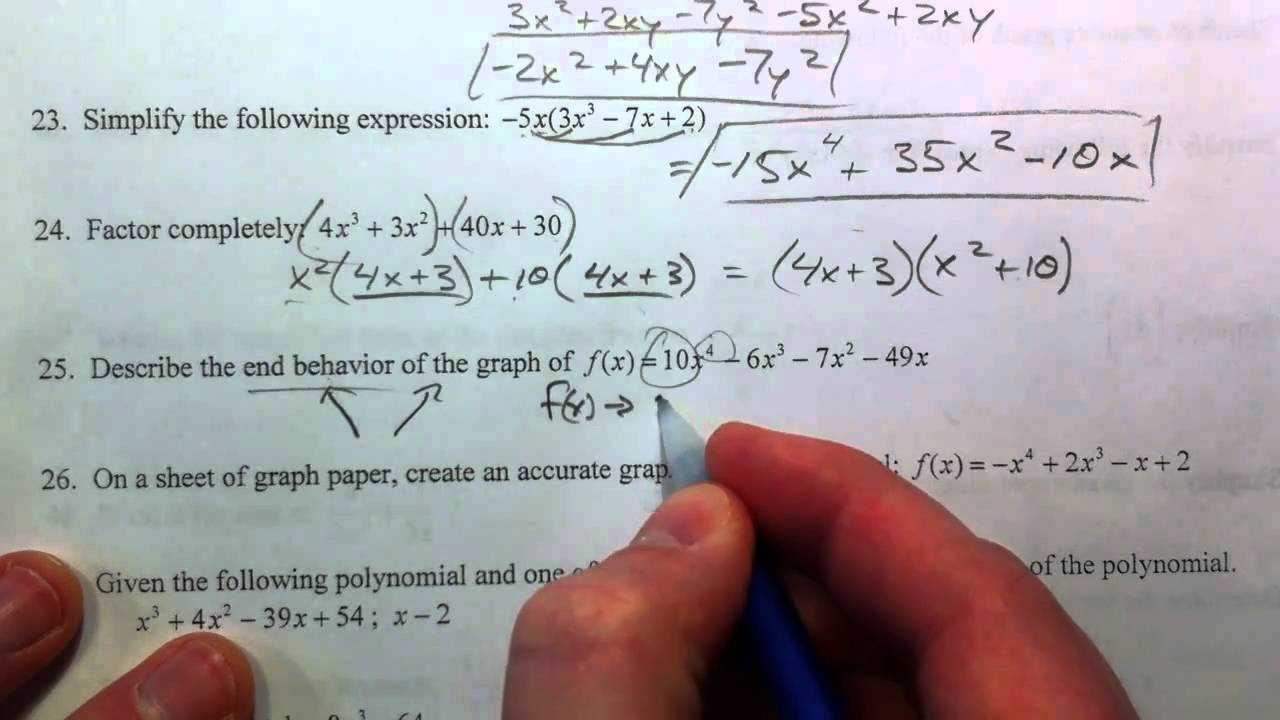
Exponential functions describe processes that grow or decay at a constant rate. They are typically represented in the form f(x) = a * b^x, where a is the initial value, b is the base, and x is the exponent. The base b determines the rate of growth or decay: if b is greater than 1, the function represents exponential growth, and if b is between 0 and 1, it represents exponential decay.

Logarithmic Functions

Logarithmic functions are the inverse of exponential functions. They help solve equations where the unknown is in the exponent. The general form of a logarithmic function is f(x) = log_b(x), where b is the base and x is the argument. By understanding logarithms, students can find solutions to equations like b^x = y, where the logarithm provides the value of x.

Factoring Techniques You Should Know

Factoring is a fundamental skill in mathematics that simplifies expressions and equations, making them easier to solve. The process involves breaking down complex polynomials into simpler factors, which can be multiplied to recreate the original expression. Mastering different factoring techniques is essential for solving a variety of problems, from solving equations to simplifying expressions. Understanding when and how to apply each method can make solving algebraic problems more efficient and less time-consuming.

There are several key factoring techniques that every student should be familiar with. These methods are designed to handle different types of polynomials, each with its own structure. Whether working with quadratic expressions or higher-degree polynomials, knowing how to recognize patterns and apply the correct technique is crucial for success.

Understanding Systems of Equations

Systems of equations involve multiple equations that share common variables. Solving these systems means finding the values of the variables that satisfy all the equations simultaneously. These problems often arise in real-world situations where multiple conditions must be met at the same time, such as determining the intersection points of two lines or balancing chemical reactions. Understanding how to solve these systems is crucial for tackling more complex problems in mathematics and applied sciences.

Solving by Substitution

The substitution method involves solving one equation for one variable and then substituting that expression into the other equation. This technique is particularly useful when one of the equations is already solved for one variable or can easily be rearranged. By replacing the variable in the second equation, it reduces the system to a simpler equation with one unknown, making it easier to find the solution.

Solving by Elimination

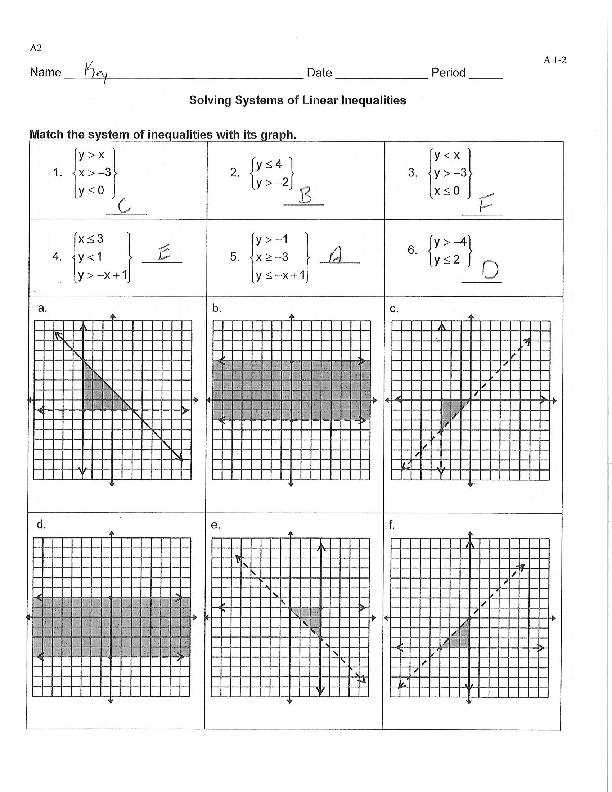
The elimination method focuses on adding or subtracting the equations in such a way that one of the variables cancels out. This approach is most effective when the coefficients of one variable are the same or opposites in both equations. Once one variable is eliminated, the system is reduced to a single equation that can be easily solved for the remaining variable.

Strategies for Solving Word Problems

Word problems can be some of the most challenging tasks in mathematics, as they require translating real-world situations into mathematical expressions. The key to solving these problems is to break them down step-by-step, carefully analyzing the information provided and identifying the relationships between variables. By employing a systematic approach, you can simplify even the most complex problems and find the solution with greater ease.

Understand the Problem

Before diving into calculations, it is essential to fully understand the problem. Read the problem carefully and identify the given information, as well as what you are asked to find. It’s often helpful to underline or highlight key data, such as numbers, units, or relationships between quantities. Once you have a clear picture of the problem, you can begin to decide what mathematical operations or methods are required to solve it.

Set Up an Equation

Once the problem is understood, the next step is to set up an equation that models the situation. Identify the variables that represent the unknowns and translate the relationships into mathematical terms. For example, if the problem involves rates, time, and distance, you might use a formula like distance = rate × time. Writing the equation is crucial for ensuring you stay on track as you work through the problem, and it helps clarify the connections between the quantities involved.

Real-World Applications of Algebra 2

The concepts learned in advanced mathematics are not just abstract ideas; they have practical applications in many fields. From engineering to economics, and from technology to healthcare, the principles explored in higher-level math are used to solve real-world problems. Understanding how to apply mathematical techniques, such as solving equations and analyzing functions, can make a significant impact in various industries and everyday life.

Engineering and Technology

In fields like engineering and technology, mathematical models are essential for designing systems, structures, and processes. Engineers often use equations to calculate stress and strain on materials, optimize production processes, or simulate real-world phenomena. For example, understanding quadratic functions is key when analyzing projectile motion, which is crucial in fields like aerospace engineering. Similarly, logarithmic functions are applied in electronics and signal processing.

Finance and Economics

In the world of finance, algebraic methods are used to calculate interest rates, analyze investments, and model financial growth. Economic models often rely on systems of equations to determine optimal resource allocation or predict future trends. Analyzing compound interest and understanding exponential growth is vital for investment strategies, while systems of equations are frequently used to model supply and demand curves in economics.

Application Area	Algebraic Concept Used	Example
Engineering	Quadratic Functions	Analyzing the trajectory of projectiles
Technology	Logarithmic Functions	Signal processing and data compression
Finance	Exponential Growth	Compound interest calculations
Economics	Systems of Equations	Modeling supply and demand

Common Mistakes in Algebra 2 and How to Avoid Them

While learning advanced mathematical concepts, students often make mistakes that can impede their understanding and progress. These errors usually stem from misinterpreting instructions, overlooking details, or failing to apply methods correctly. Recognizing these common pitfalls and learning how to avoid them can greatly improve performance and reduce frustration. Below are some frequent mistakes and tips on how to steer clear of them.

1. Misinterpreting Negative Signs

• When working with equations, it’s easy to forget the importance of negative signs, especially when dealing with subtraction or division.
• Always double-check that negative signs are correctly distributed and applied in your calculations.

2. Incorrectly Simplifying Expressions

• One of the most common mistakes is incorrectly simplifying expressions, particularly when dealing with fractions or powers.
• Be sure to follow the proper order of operations (PEMDAS) and simplify expressions step-by-step.

3. Forgetting to Check Solutions

• After solving an equation, many students fail to substitute their solutions back into the original equation to verify their correctness.
• Make it a habit to always check your solutions to ensure they satisfy the initial conditions of the problem.

4. Misapplying Formulas

• Sometimes, students apply the wrong formula or use a formula in the wrong context, especially when dealing with quadratic equations or functions.
• Ensure that you are using the appropriate formulas for the specific problem and understand how and when to apply them correctly.

5. Overlooking Domain and Range

• In some problems, especially with rational and exponential functions, the domain and range play a crucial role. Students often overlook restrictions on the variables.
• Always check for domain restrictions (e.g., denominators cannot be zero) and understand how they affect the solutions.

By being aware of these mistakes and practicing careful attention to detail, you can avoid unnecessary errors and improve your problem-solving skills.

Using Online Resources for Algebra 2

In today’s digital age, there is an abundance of online tools and resources that can enhance your understanding of complex mathematical concepts. These resources provide interactive learning experiences, tutorials, practice problems, and step-by-step solutions, making it easier for students to grasp difficult topics. By utilizing these platforms, learners can supplement their classroom instruction, engage in self-paced learning, and receive immediate feedback on their progress.

Online platforms also allow students to access a variety of learning materials, including video tutorials, quizzes, and forums where they can ask questions and discuss problems with peers or instructors. These resources are designed to support different learning styles, whether you are a visual learner, someone who benefits from hands-on practice, or you prefer detailed explanations. Additionally, they offer the flexibility to study at your own pace, anytime and anywhere.

Incorporating online resources into your study routine can not only reinforce what you’ve learned but also expose you to alternative methods of problem-solving and new strategies for tackling challenging problems. Whether you need help with understanding key concepts or preparing for exams, these tools can be incredibly useful in mastering advanced mathematical concepts.

Preparing for E2025 Algebra 2 Exams

Preparing for an advanced mathematics exam requires both careful planning and focused effort. The key to success is understanding the core concepts, practicing problem-solving techniques, and becoming familiar with the exam format. By reviewing course materials, practicing various types of problems, and managing your time effectively, you can boost your confidence and perform well during the test.

Effective Study Strategies

To ensure thorough preparation, here are some strategies to help you succeed:

• Review key concepts: Go over the fundamental principles you’ve learned throughout the course, focusing on areas that challenge you the most.
• Practice regularly: Complete practice problems daily, especially in areas where you need more improvement. This will build your confidence and sharpen your skills.
• Understand your mistakes: When you make an error, take time to review it. Understanding why you got a problem wrong helps you avoid similar mistakes in the future.
• Use available resources: Take advantage of online tutorials, videos, and practice exams. These tools can help reinforce your knowledge and provide alternate explanations.

Time Management Tips

Effective time management is crucial when preparing for exams. Here’s how to organize your study schedule:

• Create a study plan: Allocate specific time slots for studying each topic. Stick to this schedule and ensure you cover all the material before the exam date.
• Prioritize difficult topics: Focus on the areas that you find the most challenging. These might require more time and attention.
• Take breaks: Don’t forget to give yourself short breaks during study sessions. Resting your mind will help you stay focused and retain information better.
• Simulate exam conditions: Practice under timed conditions to get used to the pace of the exam and improve your time management skills.

With the right study strategies and time management, you can approach the exam with confidence and tackle each question effectively.

How to Review Algebra 2 Effectively

Effective review is essential for mastering mathematical concepts and ensuring success in exams. It involves more than just re-reading notes or doing a few practice problems. To truly understand the material and reinforce your skills, you must approach your review systematically. By focusing on key areas, practicing consistently, and using different methods of reinforcement, you can achieve a deeper understanding and prepare effectively for assessments.

Organize Your Review Materials

The first step in reviewing effectively is to organize your study materials. This allows you to know exactly what you need to focus on and track your progress:

• Gather notes and assignments: Collect all your class notes, homework assignments, and any handouts you’ve received. Having everything in one place helps you avoid wasting time searching for materials.
• Identify key concepts: Go through your notes and identify the main concepts and formulas you’ve covered. Make a list of these topics to guide your review.
• Highlight challenging areas: Mark areas where you’re struggling or that require more practice. Focus your efforts on these concepts to strengthen your weak points.

Practice and Reinforce Skills

Once you’ve organized your materials, it’s time to practice and reinforce your skills. Consistent practice is the key to improvement:

• Work through practice problems: Completing practice problems from textbooks, online resources, or past exams will test your understanding and improve your problem-solving speed.
• Review solutions: After solving practice problems, review the solutions carefully. Understand the steps and reasoning behind the answers to identify areas where you made mistakes.
• Use flashcards for formulas: Create flashcards with important formulas and concepts to help you memorize and quickly recall essential information during exams.

By organizing your study materials and engaging in focused practice, you will build confidence and improve your proficiency in mathematical topics. Regular review, along with consistent effort, will ultimately lead to success.

Tips for Improving Your Algebra 2 Skills

Mastering advanced mathematical concepts requires consistent practice, focus, and strategic learning. To improve your skills, it’s essential to break down the material, identify weak areas, and implement effective study techniques. Whether you’re struggling with specific topics or just looking to enhance your overall understanding, the following tips can help you build stronger problem-solving abilities and gain confidence in your studies.

1. Strengthen Your Foundation

Before diving into more complex topics, ensure that your foundational knowledge is solid. Many advanced concepts rely on understanding the basics, so make sure you have a strong grasp of earlier material:

• Review basic operations: Make sure you are comfortable with fundamental operations such as addition, subtraction, multiplication, and division of integers and fractions. These are the building blocks of more advanced topics.
• Understand key properties: Familiarize yourself with the properties of numbers, such as the distributive, associative, and commutative properties, which are often used in various equations and transformations.
• Practice factoring: Factorization is crucial for solving quadratic equations and simplifying expressions. Mastering this technique will be essential as you move forward.

2. Develop Problem-Solving Strategies

To become more proficient, it’s important to approach each problem with a clear strategy. Developing problem-solving skills will help you work through questions efficiently:

• Break down complex problems: Divide difficult problems into smaller, manageable steps. This will help you tackle each part of the problem without feeling overwhelmed.
• Practice regularly: The more problems you solve, the more familiar you’ll become with different types of questions and techniques. Set aside time each day to practice, even if it’s just for a few minutes.
• Learn from mistakes: Don’t be discouraged by errors. Instead, use them as learning opportunities. Review your mistakes, understand why they happened, and focus on how to avoid them next time.

Improving your skills requires time and dedication, but with consistent practice and a strategic approach, you can significantly boost your performance. Stay focused on mastering the fundamentals, and don’t hesitate to seek help when needed to ensure continued progress.