Geometry Semester 1 Exam Answers and Solutions

Preparing for a challenging assessment requires a strong grasp of key principles and the ability to apply them effectively. Whether you’re reviewing formulas, practicing techniques, or refining problem-solving skills, it’s important to approach the material systematically. A solid understanding will help you confidently navigate through complex questions and solve them with accuracy.
Effective study strategies are essential to achieving success. By focusing on the core topics, practicing frequently, and addressing any weak areas, you’ll be better prepared to handle any task that comes your way. Building confidence through repetition and understanding underlying concepts will significantly improve your performance.
In this section, we’ll guide you through crucial methods, offer tips for common challenges, and provide resources that will aid in mastering the material. Whether you’re tackling numerical problems or theoretical questions, a strategic approach can make all the difference in how you approach and complete your work.
Essential Solutions for Your Test Preparation
Successfully completing a challenging assessment relies on your ability to understand key concepts and apply them in various contexts. Knowing how to approach different types of questions and recognizing patterns within problems is crucial. This section provides essential strategies and step-by-step approaches to help you tackle any question confidently and efficiently.
Mastering Core Principles
At the heart of any rigorous test are the fundamental ideas that guide problem-solving. Whether you are dealing with calculations, proofs, or visual analysis, understanding core principles ensures that you can break down each challenge into manageable steps. Being familiar with essential formulas and theorems will make tackling questions faster and more accurate.
Strategic Problem-Solving Techniques
To maximize efficiency during the test, it’s important to implement strategic problem-solving techniques. Organizing your approach by first identifying the question type and then applying the most relevant method allows you to maintain focus. Time management is key, and by practicing regularly, you’ll develop the ability to quickly assess and solve problems with precision.
Key Concepts to Master Before the Test
Before tackling any challenging assessment, it is crucial to focus on mastering the core ideas that will guide your success. A strong understanding of these essential principles allows you to approach each question with confidence and clarity. Whether dealing with calculations or logical reasoning, these concepts are foundational for achieving accuracy and efficiency.
Core Areas to Focus On
To prepare effectively, focus on mastering the following key areas:
- Basic Theorems and Formulas: Familiarity with essential rules and equations is vital for quick problem-solving.
- Visual Representation: Understanding how to interpret and draw diagrams will aid in identifying relationships between elements.
- Logical Reasoning: Strengthening your ability to form clear, step-by-step solutions is crucial for complex tasks.
Practical Application and Techniques
Beyond theoretical knowledge, you must also practice applying these concepts in different scenarios. The following techniques are essential:
- Breaking Down Problems: Approach each question by separating the known and unknown variables to simplify the task.
- Using Visual Aids: Sketching diagrams or making charts can help clarify complex relationships between elements.
- Time Management: Practice solving problems within a set timeframe to develop speed and accuracy.
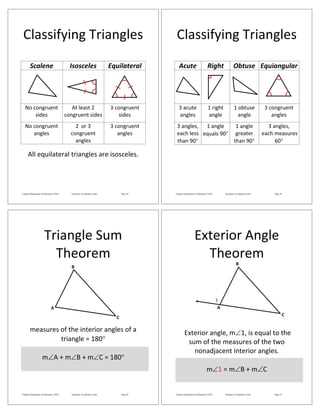
Important Theorems to Remember for Your Test
Mastering key theorems is essential for tackling a wide range of problems. These fundamental principles serve as the foundation for solving complex tasks and help you recognize patterns quickly. A solid understanding of the most important theorems will allow you to approach any challenge with greater confidence and precision.
Essential Theorems to Know
Focus on the following theorems, as they are frequently applied in various types of problems:
- Pythagorean Theorem: Relates the sides of a right triangle and is crucial for distance and area calculations.
- Triangle Sum Theorem: States that the interior angles of any triangle add up to 180 degrees.
- Congruence Postulates: Determine when two shapes are identical in size and shape, often used in proofs.
- Parallel Line Theorems: Involve the properties of angles formed by parallel lines and transversals.
- Angle Bisector Theorem: Helps find relationships between angles and side lengths when a bisector divides an angle.
How to Apply These Theorems
Understanding how and when to apply these theorems is equally important. Use the following strategies to integrate them effectively:
- Identify Relationships: Look for right angles, parallel lines, or congruent triangles in the problem to recognize applicable theorems.
- Use Theorems in Proofs: Applying these principles in logical sequences will help prove more complex results.
- Combine Theorems: Often, multiple theorems can be combined to solve a problem. Practice combining them for more advanced challenges.
Step-by-Step Guide to Solving Problems
When approaching complex tasks, a systematic approach is key to success. Breaking down a problem into smaller, more manageable steps helps clarify the process and ensures that no detail is overlooked. This guide will outline the essential steps for effectively solving challenges, allowing you to achieve accurate and reliable results.
Step 1: Understand the Problem
The first step in solving any problem is to fully understand what is being asked. Carefully read the question and identify the key elements involved, such as the shapes, angles, or measurements provided. Highlight the known information and mark what needs to be determined.
Step 2: Choose the Appropriate Strategy
Once you’ve identified the problem, determine the best method or formula to apply. Whether using algebraic equations, geometric properties, or visual tools, the right strategy is crucial to simplifying the solution process.
| Problem Type | Strategy |
|---|---|
| Distance/Length Calculation | Use the Pythagorean theorem or distance formulas. |
| Angle Measurement | Apply angle relationships like complementary and supplementary angles. |
| Area/Perimeter | Use appropriate area and perimeter formulas based on the shape. |
Step 3: Solve and Verify
Apply the chosen strategy to solve the problem step by step. Work carefully, showing all calculations and reasoning. After completing the solution, review your work to ensure that all steps were followed correctly and that the answer makes sense in the context of the problem.
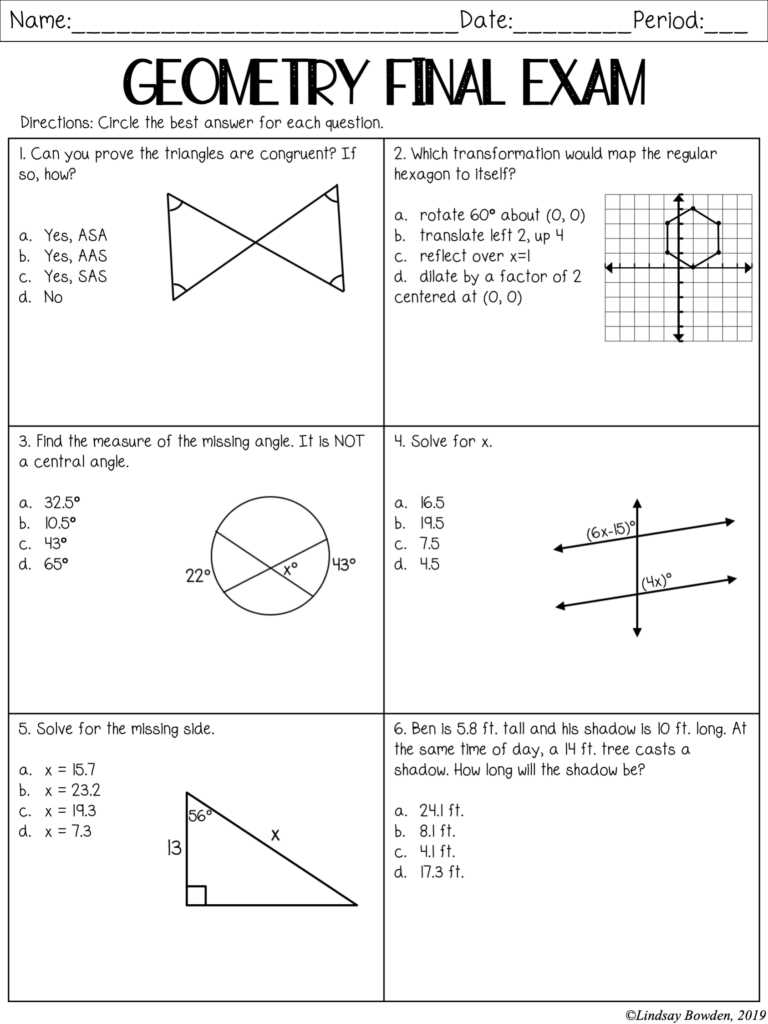
Common Mistakes to Avoid on the Test
When facing a challenging assessment, it’s easy to make simple errors that can cost valuable points. These mistakes often arise from rushing, misinterpreting the problem, or overlooking important details. Being aware of the common pitfalls can help you avoid them and improve your overall performance.
One of the most frequent mistakes is failing to read the question carefully. Often, students miss key information or misinterpret what is being asked. Always take your time to understand exactly what needs to be solved, and be sure to highlight important facts.
Another common issue is forgetting to apply the correct formulas or principles. It’s crucial to recall the relevant rules for each problem and use them correctly. Skipping steps or applying the wrong formula can lead to incorrect answers, even if the calculations themselves are accurate.
Finally, be cautious of calculation errors, especially when dealing with complex equations. Double-check your work and make sure that all operations are performed in the correct order. Small mistakes, such as misplacing a decimal or forgetting a negative sign, can quickly add up and affect your final answer.
How to Approach Multiple Choice Questions
Multiple choice questions often appear to be simple, but they require a strategic approach to avoid common traps. The goal is not just to guess but to apply your knowledge efficiently and eliminate incorrect options to increase your chances of selecting the correct answer. Here are a few tips to help you handle these questions effectively.
Step 1: Read the Question Carefully
Before looking at the answer choices, read the question thoroughly to understand exactly what is being asked. Pay attention to keywords and specific instructions. Sometimes, the question may contain hints that can guide you toward the correct response.
Step 2: Eliminate Clearly Wrong Answers
Start by eliminating answers that are obviously incorrect. This narrows down your choices and increases the likelihood of choosing the correct option. Look for answers that contradict the facts or logical reasoning presented in the problem.
Step 3: Use Logical Reasoning
If you’re unsure about the answer, apply your knowledge of key principles or use the process of elimination. Often, there will be one option that doesn’t quite fit with the information or has an obvious mistake. Logical reasoning will help you spot this and make a more informed decision.
Step 4: Don’t Overthink
Multiple choice questions are designed to test your ability to recall information quickly and accurately. Overthinking can lead to confusion. If you have a strong understanding of the material, trust your first instinct, and don’t second-guess yourself too much.
Step 5: Double Check Your Work
If time allows, double-check your selected answer before moving on. Ensure that you haven’t missed anything important in the question or made a small mistake while reading the choices.
Tips for Solving Proof-Based Questions
Proof-based questions require a clear, logical approach to demonstrate the validity of a given statement. These problems assess your ability to reason step-by-step and apply fundamental concepts systematically. The key to success is breaking down the problem into smaller parts, ensuring each step is supported by a valid argument or theorem.
Start by identifying the given information and what needs to be proven. Understanding the relationship between the given elements is crucial to constructing a strong argument. Often, diagrams can provide helpful insights into how to approach the problem.
Next, recall the relevant theorems or properties that may apply to the situation. The most effective proofs are based on well-known principles, so being familiar with common rules and postulates will streamline the process.
When constructing your proof, be sure to organize your work logically. Begin with the known information and move step-by-step toward the conclusion. Each step should be supported by a clear justification, whether it’s a definition, theorem, or previous step. Avoid skipping any steps, even if they seem obvious, as clarity is key to a strong proof.
Lastly, always review your proof once you’ve completed it. Check that each logical step follows correctly and that your reasoning is sound. Small errors in logic can invalidate an entire argument, so careful verification is essential.
Essential Formulas to Know for Your Test
Having a solid grasp of key formulas is crucial for solving problems efficiently and accurately. These formulas provide the foundation for a variety of problems, from calculating areas and volumes to working with angles and lengths. Familiarity with these essential expressions will help you approach tasks with confidence and speed.
Basic Area and Perimeter Formulas
- Area of a Rectangle: A = length × width
- Area of a Triangle: A = 1/2 × base × height
- Perimeter of a Rectangle: P = 2 × (length + width)
- Perimeter of a Circle: P = 2π × radius
- Area of a Circle: A = π × radius²
Important Volume and Surface Area Formulas

- Volume of a Cube: V = side³
- Volume of a Rectangular Prism: V = length × width × height
- Surface Area of a Sphere: SA = 4π × radius²
- Volume of a Cylinder: V = π × radius² × height
- Surface Area of a Cylinder: SA = 2π × radius × height + 2π × radius²
Key Theorems and Relationships
- Pythagorean Theorem: a² + b² = c² (for right triangles)
- Angle Sum of a Triangle: 180° (the sum of interior angles)
- Exterior Angle Theorem: Exterior angle = sum of two opposite interior angles
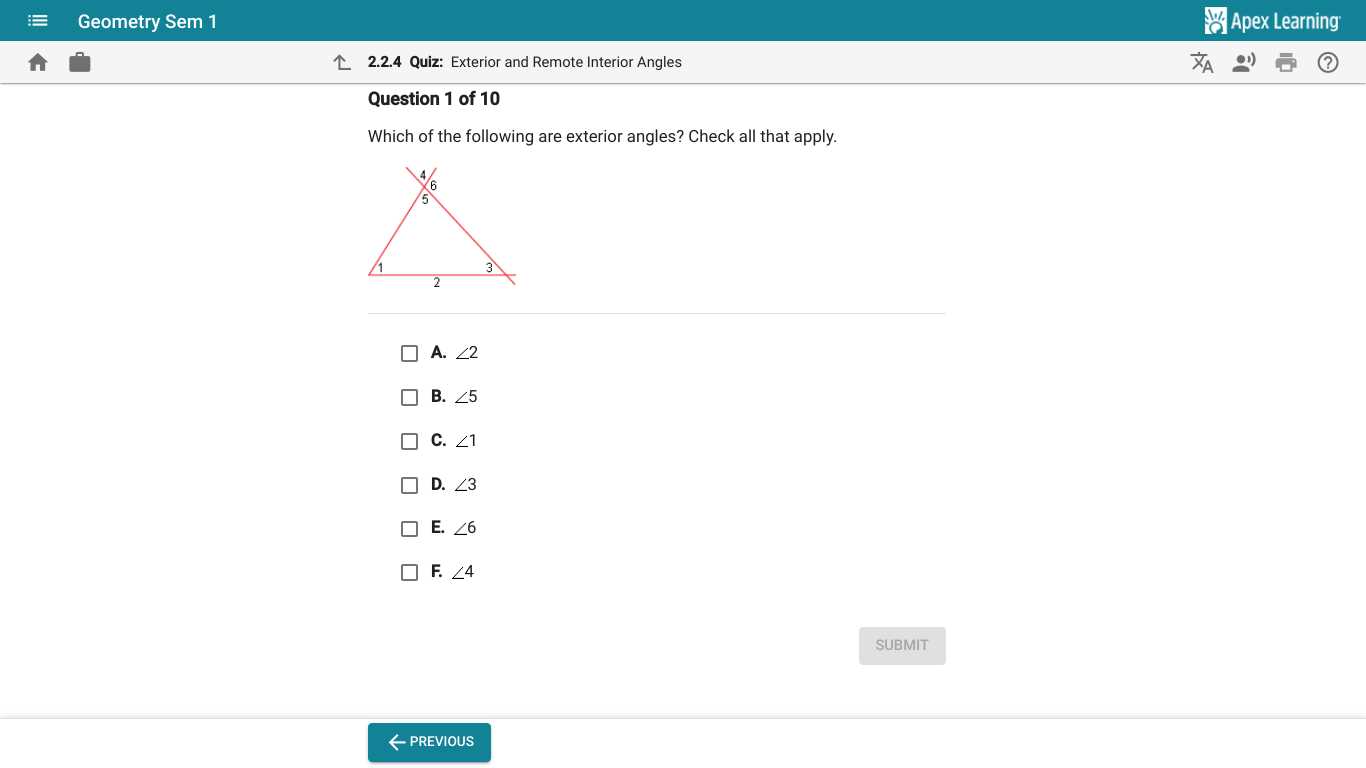
Understanding Diagrams and Visuals
Interpreting diagrams and visuals is a crucial skill when tackling problems that require spatial reasoning. Often, a well-drawn diagram can provide immediate insight into the relationships between different elements and help clarify the problem. The key is to carefully analyze the visual representation and extract relevant information from it.
Reading Diagrams Effectively
Start by identifying all the labeled elements within the diagram. These labels often indicate important measurements, such as lengths, angles, or areas. Be sure to notice any markings that suggest specific properties, like parallel lines, right angles, or congruent shapes.
Next, analyze the relationships between the different parts of the diagram. Are there any geometric rules or theorems that apply? For example, parallel lines may suggest the use of alternate interior angles or corresponding angles. Understanding these connections can help you approach the problem more logically.
Using Visuals to Solve Problems
Visuals often provide a way to break down complex problems into simpler components. For instance, identifying similar or congruent shapes in the diagram can help you apply proportional relationships or symmetry. Look for patterns or specific characteristics that can guide your solution process.
| Element | Possible Implication |
|---|---|
| Right Angles | Use the Pythagorean Theorem or trigonometric ratios. |
| Parallel Lines | Apply properties of corresponding or alternate interior angles. |
| Congruent Triangles | Apply congruence postulates (SSS, SAS, ASA, AAS). |
| Circles | Use formulas for area, circumference, and central angles. |
By carefully examining each visual, you can often find direct connections to the concepts you’ve studied, allowing you to solve problems efficiently and accurately.
Time Management Tips for Tests
Effective time management is key to success when facing assessments that require both critical thinking and problem-solving skills. When working under time constraints, it’s important to balance speed with accuracy. The goal is not just to complete the tasks but to approach them strategically, ensuring that you can apply the right methods efficiently without rushing.
Prioritize the Questions
Start by quickly scanning through the entire test. Identify the questions that you can answer with ease and those that may require more time. Tackling the simpler problems first gives you confidence and ensures that you accumulate points quickly.
Once you’ve completed the easier questions, move on to more complex ones. If you find yourself stuck on a particular problem, don’t dwell on it for too long. Mark it and come back later after addressing other questions.
Manage Your Time for Each Section
Allocate a set amount of time for each section or group of questions. For example, if the test is divided into multiple sections, decide beforehand how much time to dedicate to each. Keep an eye on the clock to make sure you’re staying on track.
| Section | Suggested Time Allocation |
|---|---|
| Easy Questions | 5-10 minutes |
| Moderate Difficulty | 10-20 minutes |
| Challenging Questions | 15-30 minutes |
| Reviewing and Final Checks | 5-10 minutes |
By carefully dividing your time based on difficulty, you can ensure that you don’t spend too much time on one section at the expense of others.
Stay Calm and Focused
Time pressure can sometimes lead to anxiety, but it’s essential to remain calm and composed. Taking deep breaths and staying focused on the task at hand can help you maintain clarity and avoid unnecessary mistakes. Use your time wisely, and always leave a few minutes at the end to review your work for any errors or overlooked details.
Strategies for Studying Effectively
Mastering complex subjects requires a focused approach to studying, especially when dealing with topics that involve both logical reasoning and spatial understanding. The key is to break down challenging concepts into manageable chunks and approach each topic systematically. Effective preparation involves practicing a variety of problems, understanding the underlying principles, and consistently reviewing material.
Set a Consistent Study Schedule
Consistency is essential when it comes to studying for subjects that require both memorization and application. Set aside dedicated time each day to review and practice problems. A consistent study routine allows you to gradually build knowledge without overwhelming yourself.
- Study for 30-45 minutes at a time with short breaks in between.
- Focus on one topic per session to avoid distractions and confusion.
- Review previous material regularly to reinforce your memory.
Practice with Different Types of Problems
To strengthen your problem-solving abilities, it’s essential to practice a wide range of questions. This ensures that you understand not only the specific methods but also how to apply them in various contexts.
- Start with basic problems to ensure a solid understanding of the fundamentals.
- Gradually move to more complex questions that challenge your reasoning skills.
- Work on problems that require multiple steps to develop your ability to think critically.
Use Visual Aids and Diagrams

Many concepts can be better understood when visualized. Use diagrams and visual aids to help reinforce the relationships between different elements. Drawing diagrams or sketching out problems can clarify complex ideas and reveal patterns that are not immediately apparent from the text.
Review Key Concepts and Theorems
Understanding the foundational principles and theorems is crucial for success. Make sure you spend time memorizing and understanding the core concepts that frequently appear in problems. Create flashcards or summary sheets to quickly review these concepts.
- Focus on important formulas and rules.
- Practice applying these rules to real-world scenarios.
- Regularly test your understanding by explaining concepts aloud or to a study partner.
Study with Others
Sometimes, studying with others can provide new perspectives and insights. Group study sessions allow you to discuss difficult concepts and share problem-solving strategies. Just ensure that the study session stays focused on the material and that everyone actively participates.
How to Tackle Word Problems in Geometry

Word problems often present unique challenges because they require not only an understanding of concepts but also the ability to translate real-world scenarios into mathematical terms. The key to solving these types of problems is to break them down step by step, carefully identifying the relevant information and applying the correct methods. With the right approach, even the most complex word problems can become manageable.
Start by carefully reading the problem, making sure to highlight or underline important details. Look for key phrases that indicate specific actions, such as “find,” “calculate,” or “determine.” These cues will guide your approach to the problem. Next, visualize the situation if possible. Sketching a diagram can often reveal important relationships that are not immediately obvious in the text.
Once you have a clear understanding of the problem, write down any known values and variables. This will help you organize your thoughts and create a plan of action. Identify the relationships between the given information and the unknowns, and choose the appropriate formulas or methods to use. Be sure to check your work at each stage to ensure you are moving in the right direction.
Lastly, practice is essential. The more word problems you work through, the better you will become at identifying patterns and applying strategies effectively. By consistently practicing different types of problems, you can develop the skills needed to tackle even the most challenging word problems with confidence.
Using Practice Tests to Prepare for the Exam
One of the most effective ways to prepare for any assessment is by taking practice tests. These tests help familiarize you with the format, improve time management skills, and identify areas where you may need more practice. By simulating real testing conditions, practice tests provide valuable insights into how well you have mastered the material and how you can improve your approach.
Benefits of Practice Tests
When you engage with practice tests, you’re not just reviewing concepts but actively applying them under timed conditions. This helps reduce test anxiety and builds confidence as you become more comfortable with the format and types of questions likely to appear.
- Improves familiarity with the test format and question styles.
- Helps identify weak areas that need additional study.
- Builds confidence and reduces anxiety by simulating real exam conditions.
How to Use Practice Tests Effectively
Simply taking a practice test isn’t enough–you need to review your results thoroughly. After completing a practice test, carefully go over the questions you got wrong and understand why the correct answers are what they are. This review process is crucial for reinforcing concepts and ensuring that you won’t make the same mistakes during the actual assessment.
- Set a time limit to simulate real test conditions.
- Review your incorrect answers and understand the mistakes made.
- Focus on areas of weakness by taking targeted practice tests in those topics.
By regularly incorporating practice tests into your study routine, you can track your progress, refine your test-taking strategies, and increase your chances of success on the actual assessment.
How to Check Your Answers in Geometry
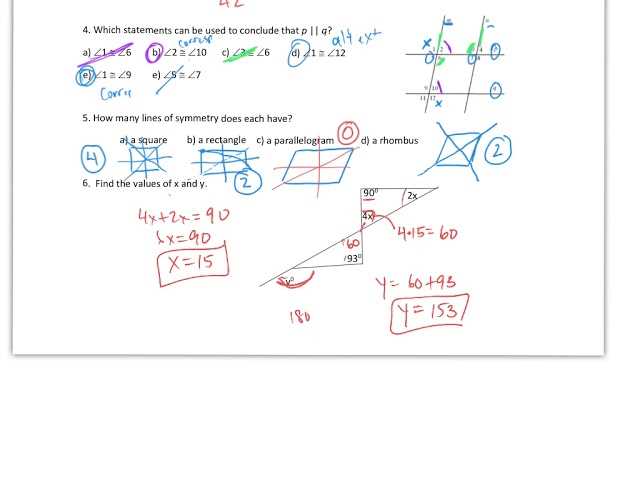
Reviewing and verifying your solutions is a crucial step in ensuring accuracy. Even if you feel confident in your work, mistakes can sometimes go unnoticed. To effectively check your solutions, it’s important to follow a structured approach that focuses on the reasoning behind each step, not just the final result. This will help you catch any errors early and ensure the integrity of your calculations.
Step-by-Step Verification Process
Start by revisiting the problem statement and confirming that you’ve addressed all parts of the question. Ensure that you’ve used the correct formulas or principles and that the relationships between different elements are clear. Once you’ve reviewed the process, retrace your steps to check for simple arithmetic mistakes, such as calculation errors or incorrect signs.
| Step | What to Check |
|---|---|
| Step 1 | Review the problem statement to ensure all parts are addressed. |
| Step 2 | Verify that the correct formulas or principles were applied. |
| Step 3 | Revisit your calculations and check for any simple arithmetic mistakes. |
| Step 4 | Ensure all units are consistent and correctly applied. |
Double-Checking for Consistency
It’s also important to confirm that your results make sense in the context of the problem. Are the values you’ve obtained reasonable based on what you know about the situation? For example, if you’re solving for the length of a side of a triangle, does the result match the expected range based on the given dimensions? If something seems off, it’s worth re-examining your work to catch any overlooked mistakes.
Finally, if possible, compare your results with another method or source, such as a classmate’s solution, textbook examples, or an online calculator. This comparison can help you spot any inconsistencies and ensure that your solution is correct.
Geometry Exam Tips for Nervous Students
Feeling anxious before a test is a common experience, especially when it involves complex concepts and intricate problem-solving. However, with the right strategies, you can manage your stress and approach the assessment with confidence. The key is preparation, mindset, and knowing how to handle the pressure during the test.
Start by organizing your study materials and creating a realistic revision plan. Breaking down the material into manageable sections allows you to focus on one concept at a time, rather than feeling overwhelmed by the scope of the subject. Consistent practice will help reinforce your understanding, so spend time working through sample problems and reviewing key principles.
Another effective technique is practicing mindfulness. Before the test, take a few deep breaths to calm your nerves. Visualization can also be helpful–imagine yourself confidently solving problems and staying focused throughout the test. This mental preparation can make a significant difference in how you approach the questions when the time comes.
During the test, if you feel stuck on a problem, don’t panic. Move on to another question and come back to the challenging one later. Often, taking a short break and focusing on a different problem can help you clear your mind and return with a fresh perspective. Remember, tests are designed to assess your knowledge, not to intimidate you.
Finally, maintain a positive attitude. Trust in the effort you’ve put into your preparation, and remind yourself that mistakes are part of the learning process. By staying calm and focused, you’ll be able to approach each question methodically and demonstrate the full extent of your knowledge.
What to Do After Completing Your Geometry Exam
Once you’ve finished your test, it’s natural to feel a mix of emotions–relief, uncertainty, or even second-guessing your answers. However, it’s important to remember that the time after completing your test is just as crucial as the preparation itself. Here’s how to manage those post-assessment moments effectively.
Stay Calm and Avoid Overthinking
The first step is to resist the urge to overanalyze your responses. It’s easy to begin second-guessing your choices or worrying about mistakes. Instead, take a deep breath and remind yourself that the test is behind you. Whether you think you did well or not, the outcome is already determined, and excessive worry won’t change anything.
Review Your Approach for Future Improvement
Once you’ve let go of the test, it’s an excellent opportunity to reflect on your process. Think about what strategies worked well for you, what didn’t, and where you could improve next time. If you felt confident in your approach, that’s a positive takeaway, and you can carry that forward. If certain areas were more challenging, consider reviewing those topics and finding new methods of understanding them for future assessments.
Focus on the Next Step
While it’s tempting to dwell on your performance, it’s more productive to focus on what comes next. If you have other upcoming tasks or responsibilities, begin organizing your time around those. Shifting your focus will help you regain a sense of control and prevent unnecessary stress.
Give Yourself Time to Relax
Remember that after completing a test, especially a challenging one, you deserve time to relax and recharge. Take a break, engage in an activity you enjoy, and refresh your mind. It will help you return to future tasks with a clear, positive mindset.