Chapter 8 Loans Answer Key and Solutions

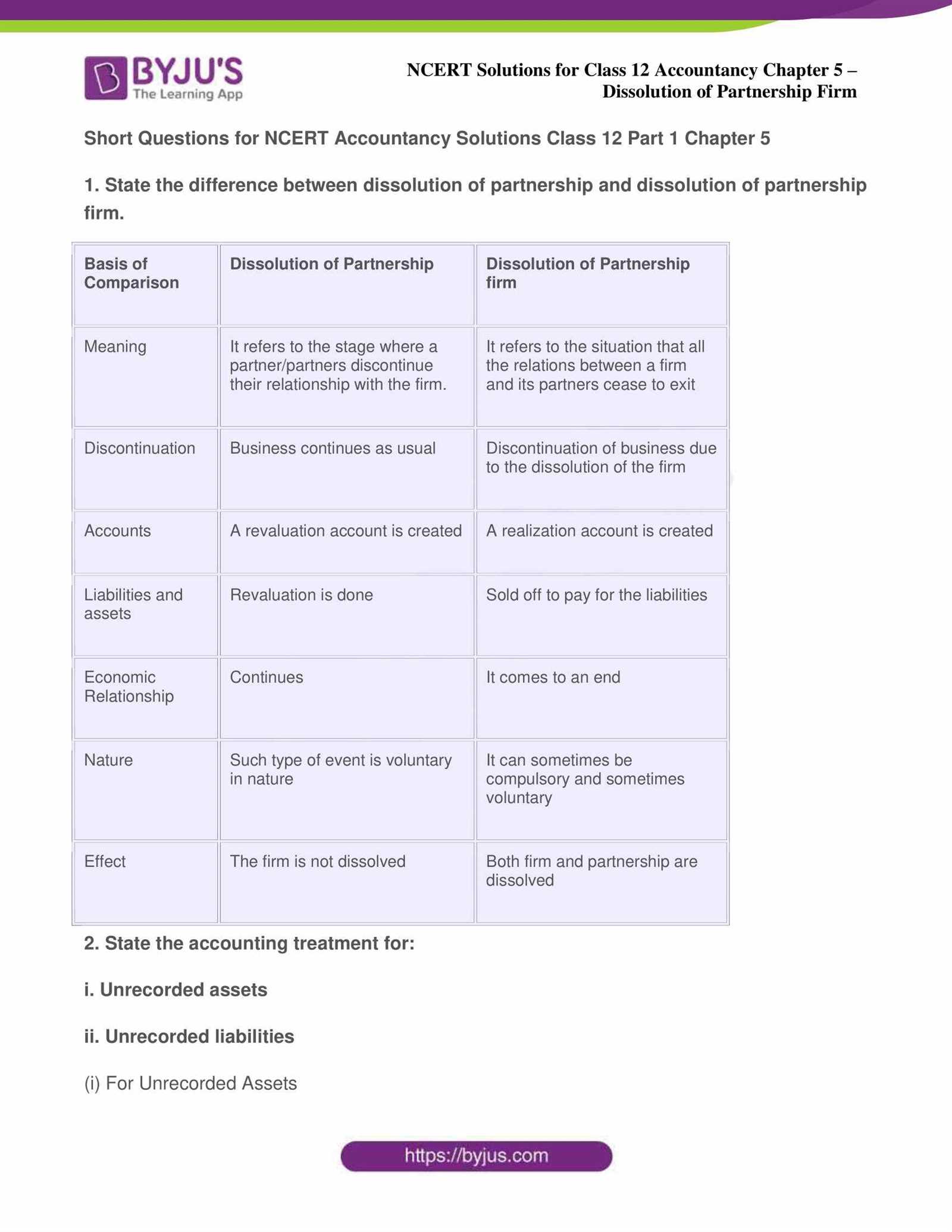
In this section, we explore essential techniques and methods for solving complex financial problems related to borrowing and repayment. Mastering these concepts is crucial for anyone looking to develop a strong foundation in financial analysis and decision-making. Whether you’re calculating monthly payments or understanding the implications of different interest rates, this guide provides the tools you need to navigate through these calculations with confidence.

Through step-by-step instructions, we break down the process of determining the various components of a financial agreement, such as principal, interest, and repayment schedules. You will learn how to approach these questions strategically and how to avoid common pitfalls in your calculations.

Our comprehensive guide also includes practical examples and exercises to reinforce the concepts discussed. These real-world scenarios will help you grasp the impact of different financial terms and prepare you for more advanced financial challenges in the future.

Chapter 8 Financial Problem Solutions Overview

This section delves into the comprehensive solutions for the various financial challenges covered in this module. Understanding the process behind these solutions is vital for applying theoretical knowledge to real-world financial scenarios. By breaking down complex calculations and procedures into simple steps, it provides a clear path for tackling similar problems efficiently.

The following content will guide you through a range of example problems, offering detailed steps for finding the correct outcomes. Whether you’re dealing with interest rates, repayment schedules, or principal balances, this overview helps clarify the essential methods and approaches needed for successful problem-solving.

Key Aspects of Financial Calculations

To fully grasp the steps involved, it’s important to recognize the main components in financial computations, such as principal, interest rates, and time periods. These elements serve as the foundation for almost every problem in this area. The table below outlines the most common variables and their roles in the calculation process:

Variable	Description	Example Value
Principal	The original amount of money borrowed or invested	$1,000
Interest Rate	The percentage charged on the principal for borrowing or investing	5%
Time Period	The duration over which the money is borrowed or invested	3 years
Monthly Payment	The fixed amount paid periodically until the loan is fully repaid	$30

Steps to Find Accurate Solutions

Now that the fundamental variables are clear, the next step is to explore the methodical approach to solving these types of financial problems. By understanding the relationships between these elements and applying the correct formulas, you’ll be able to find the accurate outcomes for any given scenario. This process is essential for anyone aiming to build expertise in financial analysis and planning.

Key Concepts in Financial Problem Solving

Understanding the foundational principles behind financial calculations is essential for accurately resolving complex problems in this area. The concepts introduced in this section provide the tools needed to approach real-world financial challenges effectively. By focusing on the core ideas, anyone can gain a deeper understanding of how to navigate the intricacies of borrowing, repayment, and interest calculations.

The following are the most important ideas you will encounter in this section:

• Principal Amount: The initial sum of money involved in the transaction, whether it’s being borrowed or invested.
• Interest Rate: The percentage of the principal charged as a fee for borrowing, which can significantly affect the total repayment amount.
• Time Period: The duration over which the financial agreement is active, often influencing the repayment schedule and interest accrual.
• Amortization: The process of paying off debt through regular installments, including both principal and interest components.
• Repayment Schedule: A plan outlining how payments are structured over time, often detailing the amount due periodically and the duration of the loan.

Additionally, understanding how these concepts interact with one another is critical for correctly solving financial problems. Below are a few key points to keep in mind:

1. The relationship between principal and interest determines the total cost of borrowing.
2. Time periods influence how interest is compounded and how payments are spread out.
3. Different types of financial agreements may require distinct approaches, such as simple interest versus compound interest calculations.

By mastering these concepts, you can approach any financial calculation with confidence and accuracy, ensuring you arrive at the correct solutions each time.

Understanding Financial Terms and Definitions

In this section, we will explore the essential terminology that forms the foundation of financial calculations and agreements. Grasping these terms is crucial for successfully navigating the intricacies of borrowing, repayment, and interest. Each concept plays a vital role in determining how money is borrowed, how interest is charged, and how payments are structured over time.

Common Terms in Financial Agreements

Below are some of the most frequently used terms that you will encounter in financial contexts:

• Principal: The original amount of money that is either borrowed or invested, excluding interest or additional charges.
• Interest: A fee charged for the use of borrowed money, typically expressed as a percentage of the principal amount.
• Term: The duration of time over which the financial agreement remains in effect, usually influencing the amount and frequency of payments.
• APR (Annual Percentage Rate): The yearly interest rate charged on a loan, including any fees or additional costs that may be incurred.
• Amortization: The process of gradually repaying the principal and interest over the term of the agreement, typically in fixed installments.

How Definitions Affect Financial Calculations

Each of these terms impacts the calculations required to determine monthly payments, total interest, and overall repayment schedules. For example, a higher interest rate or a longer term will result in higher total costs over time. Understanding these definitions enables you to make informed decisions about financial commitments and accurately calculate repayment amounts.

Step-by-Step Solutions for Financial Problems

In this section, we will guide you through the process of solving common financial problems by breaking down each step. The goal is to make complex calculations and concepts more manageable, ensuring that you can approach any situation with clarity and confidence. By following these systematic steps, you will be able to solve a wide range of financial scenarios accurately and efficiently.

The first step in solving any financial problem is to clearly identify the key components: the amount of money involved, the interest rate, the duration, and the type of repayment structure. Once these elements are established, you can proceed with the appropriate calculations.

For example, when determining the monthly payment for a fixed installment plan, follow these general steps:

1. Identify the principal: Determine the initial amount of money being borrowed or invested.
2. Determine the interest rate: Find the percentage that will be applied to the principal amount for borrowing costs.
3. Set the term length: Specify the duration over which the repayment will be made (e.g., 5 years).
4. Choose the payment frequency: Decide whether payments will be made monthly, quarterly, etc.
5. Apply the formula: Use the relevant formula to calculate the periodic payments, ensuring that interest and principal are considered correctly.

Once these steps are followed, you should be able to find the correct monthly payment or repayment amount for the financial agreement in question.

By repeating this process for different types of problems–such as calculating total interest paid or adjusting for changes in interest rates–you will gain a comprehensive understanding of how to handle various financial challenges.

How to Approach Financial Calculation Questions

When faced with financial calculation problems, it is important to approach them in a systematic way. Understanding the underlying principles and recognizing the essential elements of each scenario allows for accurate and efficient solutions. Breaking down the problem into smaller steps helps ensure that nothing is overlooked and that all necessary calculations are completed correctly.

The first step is to carefully read through the problem to identify the key information: the initial amount, the rate, the time frame, and the payment structure. Once these components are understood, it becomes easier to determine which formula or method to apply. In most cases, financial problems involve basic arithmetic and algebraic equations, but knowing which formula to use is essential for finding the right answer.

Next, focus on how the components interact with each other. For instance, an increase in the interest rate or the duration of the agreement can significantly impact the total cost or monthly payment. Understanding the relationships between the terms is crucial for accurate calculations.

Finally, check your results to ensure they make sense within the context of the problem. It’s always a good idea to verify your solution by going through the steps again or using alternative methods to cross-check the calculations.

Common Mistakes in Financial Calculations

Financial calculations can be tricky, and even small errors can lead to significant discrepancies in results. Understanding the most common mistakes made during calculations is essential for improving accuracy and avoiding costly errors. By recognizing these pitfalls, you can approach problems with greater confidence and ensure the correct solution every time.

One of the most frequent errors is misapplying the formula. For instance, using the wrong equation for compound interest instead of simple interest, or neglecting to adjust for compounding periods, can lead to incorrect results. Another common issue is failing to properly account for the time frame–confusing months with years or omitting time-based adjustments can throw off the calculations.

Additionally, many make the mistake of not double-checking the units of measurement. For example, ensuring the interest rate is applied in the correct format (annual vs. monthly rate) is crucial for obtaining the right figures. Similarly, misinterpreting terms like principal and total payment amount can lead to confusion and incorrect solutions.

Lastly, rounding errors are a subtle but frequent issue, especially when dealing with long decimal places. It’s important to apply consistent rounding rules throughout the problem to avoid small discrepancies that can add up over time.

Loan Amortization Explained Simply

Amortization refers to the process of gradually repaying a debt through regular, scheduled payments. This concept is essential for understanding how the principal and interest are distributed over time in a financial agreement. Rather than making a single large payment, the amount owed is broken down into smaller installments, with each payment covering both the interest and a portion of the principal balance.

To explain this process simply, let’s break it down into key components:

• Principal: The original amount borrowed that must be repaid.
• Interest: The cost of borrowing money, paid along with the principal over time.
• Installments: Regular payments made to reduce both the interest and the principal.
• Term: The length of time over which the debt will be repaid, such as 5, 10, or 20 years.

The typical method for amortization involves setting up a fixed repayment schedule. Early payments are often weighted more heavily towards paying off interest, with a smaller portion going toward the principal. Over time, as the outstanding balance decreases, a greater portion of each payment goes toward reducing the principal, while the interest portion decreases.

Here’s how amortization works in practice:

1. The borrower agrees on a fixed interest rate and a set repayment period.
2. Each payment is calculated to ensure the loan is fully paid off by the end of the term.
3. Payments are split between paying interest and reducing the principal balance.
4. As the principal balance decreases, the interest portion of each payment becomes smaller, and the principal portion grows.

Understanding amortization is key for borrowers, as it shows how payments are structured and helps in determining the true cost of borrowing over time. It also allows borrowers to make more informed decisions about refinancing or early repayment options.

Interest Rates and Their Impact

Interest rates play a crucial role in determining the cost of borrowing and the potential returns on investments. A small change in the rate can significantly affect the overall financial burden or reward. Understanding how interest rates influence both short-term and long-term financial decisions is essential for making informed choices in any financial agreement.

The Influence of Interest Rates on Borrowing Costs

When borrowing money, the interest rate directly impacts the total amount that must be repaid. A higher interest rate means more money paid over the life of the agreement, while a lower rate reduces the cost of borrowing. Here’s how interest rates can affect financial commitments:

• Higher Interest Rates: Increase monthly payments and total repayment amounts. Borrowers may pay more in interest over time.
• Lower Interest Rates: Decrease monthly payments and total repayment amounts, making borrowing more affordable over time.
• Rate Type: Fixed rates remain constant, while variable rates can change over time, potentially increasing the cost of borrowing.

How Rates Affect Investment Returns

For investments, the interest rate can determine the rate of return. Higher rates generally lead to greater returns on savings accounts, bonds, or other interest-bearing assets. However, a higher rate may also increase the risk associated with certain investments. Here’s how interest rates impact investments:

• Higher Interest Rates: Can offer better returns on savings and fixed-income investments, but might reduce the appeal of other assets like stocks.
• Lower Interest Rates: May offer lower returns on traditional savings but can make other investments more attractive due to the potential for higher yields elsewhere.

Ultimately, interest rates influence how much borrowers pay and how much investors earn. By understanding these impacts, individuals can better navigate financial decisions, balancing between borrowing costs and investment opportunities.

Effective Strategies for Repaying Debt

Successfully managing debt repayment requires more than just making minimum payments. Implementing well-thought-out strategies can help reduce the overall financial burden and enable quicker repayment. The key to efficient debt repayment lies in understanding your financial situation, setting clear goals, and choosing a repayment method that fits your needs.

Strategies for Faster Repayment

One of the most effective ways to pay off debt faster is by increasing the amount of each payment. Even small increases can make a significant difference in the total interest paid over time. Here are some proven strategies:

• Snowball Method: Focus on paying off the smallest balance first while making minimum payments on larger debts. Once the smallest balance is cleared, move on to the next one, and so on.
• Avalanche Method: Prioritize paying off the debt with the highest interest rate first, which helps reduce the total interest paid in the long run.
• Extra Payments: If possible, make extra payments on top of your regular installments. This can reduce the principal faster, ultimately reducing the interest amount.

Managing Multiple Debts

When dealing with multiple debts, it’s important to stay organized and create a manageable plan. Here are a few tips for staying on track:

• Consolidation: Combine multiple debts into a single payment, which can make managing repayments simpler and potentially lower your interest rate.
• Debt Refinancing: Consider refinancing to secure a lower interest rate or more favorable repayment terms, which can reduce the overall cost of borrowing.
• Set Clear Milestones: Break down your repayment goal into smaller milestones to track your progress and stay motivated.

By incorporating these strategies, individuals can achieve their debt repayment goals more efficiently, reduce the total cost of borrowing, and ultimately work toward financial freedom. The key is consistency, discipline, and finding the approach that best fits one’s financial capacity and lifestyle.

Examples of Loan Problems

Understanding how to solve debt-related problems requires practice and familiarity with different types of scenarios. By working through examples, you can learn how to apply financial principles effectively and gain confidence in solving similar problems on your own. Below are several examples that demonstrate common issues encountered in financial calculations related to borrowing and repayment.

Example 1: Calculating Monthly Payments

A borrower takes out a $10,000 loan with a 5% annual interest rate, to be repaid over 3 years. To find the monthly payment, you would apply the formula for calculating payments on an installment loan, considering the interest rate and the loan term. The result will give you the fixed monthly amount that needs to be paid to clear the debt by the end of the term.

Example 2: Determining Total Interest Paid

Suppose a borrower takes a 5-year loan of $15,000 at an interest rate of 6%. To calculate the total interest paid over the life of the loan, you would subtract the original loan amount from the total amount repaid, which includes both the principal and interest. This calculation helps to understand how much the borrower ultimately pays in addition to the original amount borrowed.

Example 3: Impact of Extra Payments on Loan Term

If a borrower makes an extra payment of $500 every year towards their $20,000 loan, they can reduce both the loan balance and the time it takes to pay off the debt. By adding these extra payments, the borrower shortens the repayment period and reduces the overall interest costs. The effect of these additional payments can be demonstrated using an amortization schedule.

These examples show how different scenarios affect the calculations involved in borrowing money, and they highlight the importance of understanding financial terms and formulas to make informed decisions. By practicing with similar examples, borrowers can build a better understanding of their obligations and manage their finances more effectively.

Understanding Principal vs Interest Payments

When managing debt, it’s essential to understand the difference between the two main components of each payment: the principal and the interest. These two elements affect the way your payments are applied and influence the total amount you repay over time. Recognizing how each portion of your payment works can help you better manage your finances and make informed decisions about repayment strategies.

What is Principal?

The principal refers to the original amount of money borrowed. Each payment made towards the debt includes a portion that goes toward reducing the principal balance. Over time, as the principal decreases, the interest calculated on the remaining balance also decreases, which results in a lower interest portion in future payments. Here’s how the principal works:

• Initial Payments: At the beginning of the repayment term, the principal portion of the payment is relatively small, with a larger portion going toward interest.
• Later Payments: As the balance decreases, a larger portion of each payment goes toward the principal, and less is applied to interest.

What is Interest?

Interest is the cost of borrowing money, charged by the lender as a percentage of the outstanding loan balance. The interest portion of each payment is determined based on the interest rate and the remaining balance. Initially, interest payments tend to be higher, but they decrease as the principal is paid down. Here’s how the interest works:

• High Interest at the Start: In the early stages of repayment, the interest portion is larger because the loan balance is higher.
• Declining Interest: As the principal is paid off, the interest payments decrease, allowing more of the monthly payment to be applied to reducing the principal.

Understanding the balance between principal and interest payments is key to managing debt effectively. By paying attention to how interest is calculated and how the principal decreases over time, you can better strategize how to pay off your debt faster and reduce overall costs.

How to Solve Loan Word Problems

Solving word problems related to borrowing and repayment can seem daunting at first, but with a systematic approach, it becomes more manageable. The key to solving these problems lies in understanding the details presented in the question and applying the correct mathematical formulas. Whether you are calculating monthly payments, determining total interest, or figuring out the repayment period, breaking down the problem into smaller, logical steps is crucial.

Step-by-Step Approach

Follow these steps to solve most borrowing-related word problems:

• Read the Problem Carefully: Start by identifying the key information such as the amount borrowed, interest rate, payment terms, and any specific time frame provided.
• Identify the Formula: Based on the type of question, determine which formula you need. Common formulas include those for calculating monthly payments, interest, or the total cost of the loan.
• Plug in the Numbers: Substitute the known values (amount, interest rate, term length) into the formula. Be sure to convert the interest rate into the correct format, such as a decimal, if needed.
• Solve the Problem: Perform the calculations carefully, step by step, to find the answer.
• Check Your Work: Always review your calculations to ensure they make sense. Double-check for any errors in the formula or miscalculations in the steps.

Example Problem

Let’s consider a simple example:

• Problem: A person borrows $5,000 at an interest rate of 6% per year for 3 years. How much will the monthly payment be?
• Solution: Use the monthly payment formula for an installment loan:

Monthly Payment = [P * r * (1 + r)^n] / [(1 + r)^n - 1]

Where:

• P is the principal ($5,000)
• r is the monthly interest rate (6% annual rate divided by 12 months, or 0.005 per month)
• n is the number of payments (3 years * 12 months = 36 payments)

After plugging in the values, the monthly payment will be calculated as $152.62.

By following these steps and practicing with different scenarios, you can become more proficient at solving word problems involving borrowing and repayments. The more you practice, the easier these types of problems become to solve, and you will develop a deeper understanding of the underlying financial principles.

Loan Formulas and How to Use Them

Understanding and using the correct formulas is essential for calculating various aspects of debt repayment. Whether you are determining monthly payments, the total amount paid over the life of a debt, or the interest accrued, these formulas help simplify complex calculations. In this section, we will discuss the most commonly used formulas and how to apply them effectively to solve problems related to borrowing and repayments.

Key Formulas for Debt Calculations

There are several important formulas to know when working with borrowing and repayments. Below are the most frequently used formulas:

• Monthly Payment Formula: Used to calculate the monthly payment for an installment loan. The formula is:

M = P * r * (1 + r)^n / [(1 + r)^n - 1]

Where:

• M = Monthly payment
• P = Principal amount (initial loan)
• r = Monthly interest rate (annual rate divided by 12)
• n = Total number of payments (loan term in months)

• Total Interest Formula: This formula helps calculate the total amount of interest paid over the life of the debt:

Total Interest = (M * n) - P

Where:

• M = Monthly payment
• n = Total number of payments
• P = Principal amount

How to Apply These Formulas

To use these formulas, you simply need to plug in the relevant numbers based on the specific loan details you are working with. Here’s an example:

• Example: A person borrows $10,000 at 5% annual interest for 3 years. To calculate the monthly payment:

M = 10000 * (0.05 / 12) * (1 + (0.05 / 12))^(3 * 12) / [(1 + (0.05 / 12))^(3 * 12) - 1]

By solving this, you find the monthly payment to be approximately $299.71.

Understanding how to apply these formulas will allow you to make accurate financial calculations and better understand the implications of borrowing. Whether for personal or business finance, mastering these formulas is a key skill for anyone dealing with debt repayment.

Practical Applications of Loan Knowledge

Understanding the principles behind borrowing and repayment is essential for making informed financial decisions. Knowledge of how to calculate payments, interest rates, and loan terms can help individuals and businesses manage their finances more effectively. This section explores the practical applications of this knowledge in various real-world scenarios, from personal finance to business investments.

Personal Finance Management

In personal finance, understanding borrowing terms can guide decisions about mortgages, car loans, and credit card debt. For instance, knowing how interest rates affect long-term payments can help individuals choose the most cost-effective loan options. Below is an example of how interest accumulation works with different loan types:

Loan Type	Loan Amount	Annual Interest Rate	Loan Term (Years)	Total Interest Paid
Mortgage	$200,000	4.5%	30	$164,000
Car Loan	$20,000	6.0%	5	$3,600
Personal Loan	$5,000	8.0%	3	$720

This table shows how different loan amounts, interest rates, and terms can impact the total interest paid. By understanding these factors, individuals can make better choices about how much to borrow and how long to commit to payments.

Business Financing

In business, loan knowledge plays a critical role in securing capital for expansion, equipment purchases, or operational costs. Understanding the cost of borrowing can help business owners assess whether taking on debt is a sound financial decision. Properly calculating payments and interest obligations ensures that businesses avoid overextending themselves and can plan for future cash flows more accurately.

For example, if a company takes out a loan to finance equipment purchases, they need to account for monthly payments, interest rates, and the depreciation of the equipment. This enables them to forecast expenses and ensure that the loan is manageable within the company’s budget.

In both personal and business finance, the ability to apply loan principles directly influences the quality of financial planning and decision-making. Whether for personal growth or business expansion, understanding the nuances of borrowing is vital to ensuring long-term financial health.

Why Chapter 8 is Crucial for Finance Students

The understanding of financial concepts related to borrowing, repayment structures, and interest calculations is fundamental for anyone pursuing a career in finance. This particular section provides the foundational knowledge necessary for mastering more complex financial models and real-world scenarios. Mastery of these concepts allows students to make informed decisions regarding investments, budgeting, and managing debt, all of which are essential skills in the finance field.

Real-World Financial Applications

For finance students, comprehending how debt works is key to understanding larger financial systems, including corporate financing, real estate transactions, and consumer lending. This knowledge directly applies to industries such as banking, investment, and insurance, where professionals frequently deal with various financial products and instruments. Without a clear grasp of how different factors–like interest rates, loan terms, and payment schedules–affect overall financial planning, students may struggle in applying theory to practice.

Preparation for Advanced Financial Topics

For students advancing into more complex financial topics, such as portfolio management or risk assessment, the understanding of basic borrowing and repayment models becomes indispensable. The ability to break down a loan’s financial impact lays the groundwork for learning about things like discounted cash flows, net present value, and more sophisticated investment strategies. Below is an example of how understanding financial terms prepares students for advanced topics:

Concept	Application in Finance	Real-World Impact
Interest Rates	Impact on loan cost and profitability	Influences pricing strategies in banking and investments
Amortization	Repayment schedules and debt reduction	Determines cash flow management in businesses and personal finance
Principal vs. Interest	Understanding of cost distribution over time	Critical for setting financial priorities and managing liabilities

By mastering these fundamental concepts, finance students build a solid foundation for analyzing and evaluating more complex financial instruments and strategies. Understanding the intricacies of borrowing terms and repayment plans equips them with the skills to assess risk, calculate returns, and make informed financial decisions that are critical to success in the finance sector.

Tips for Mastering Loan Questions

Mastering financial problems related to borrowing requires a solid understanding of core principles, accurate calculation skills, and the ability to break down complex scenarios. Whether you are preparing for an exam or looking to improve your problem-solving approach, there are a few strategies that can help enhance your ability to tackle these questions confidently. By focusing on key techniques and staying organized, you can significantly improve your accuracy and efficiency in solving financial problems.

Understand the Terminology

One of the most crucial steps is to become familiar with the essential terms used in financial scenarios. Whether it’s interest rates, repayment periods, or principal amounts, knowing the definitions and their implications will provide clarity when approaching any problem.

• Principal: The original sum of money borrowed or invested.
• Interest: The cost of borrowing money, typically expressed as a percentage rate.
• Amortization: The gradual reduction of a debt over time through scheduled payments.

Break the Problem Into Manageable Steps

It can be overwhelming to face complex financial problems, but breaking them down into smaller, more manageable steps can make a significant difference. By organizing the information and focusing on one element at a time, you can ensure accuracy and avoid common mistakes.

1. Step 1: Identify the key pieces of information (e.g., interest rate, loan amount, repayment terms).
2. Step 2: Use the correct formulas to calculate interest or other relevant variables.
3. Step 3: Double-check your calculations before finalizing your answers.

By practicing regularly and following these structured methods, you will become more comfortable with financial problems and improve your overall performance in related tasks. Consistency, along with a solid grasp of the key concepts, will ensure you master these challenges efficiently.

Common Loan Types Covered in Chapter 8

Understanding the various types of borrowing options is essential for anyone dealing with financial calculations. Different borrowing methods come with unique terms, interest rates, and repayment structures, making it crucial to grasp their distinctions. In this section, we will explore the most commonly encountered forms of credit, highlighting their characteristics and how they affect borrowers. Familiarity with these options allows for better financial decision-making and accurate problem-solving when dealing with related scenarios.

Fixed-Rate Borrowing

This type of financial arrangement offers a stable and predictable payment structure. The interest rate remains constant throughout the term of the agreement, meaning the borrower’s monthly payments will stay the same. This can be advantageous for budgeting and long-term financial planning, as it removes uncertainty about future costs.

• Pros: Stability and predictability in payments.
• Cons: Potentially higher initial rates compared to variable-rate options.

Variable-Rate Borrowing

Unlike fixed-rate agreements, variable-rate borrowing involves interest rates that can change over time, depending on market conditions. While this can offer lower initial rates, the unpredictability of rate adjustments can make long-term planning more challenging. Borrowers must be prepared for possible increases in payments if rates rise.

• Pros: Lower starting rates and potential for payment reduction.
• Cons: Risk of increasing rates and higher payments over time.

Understanding the benefits and risks of each borrowing option is key to making informed choices. Whether opting for the security of a fixed rate or the flexibility of a variable rate, each option has its place in various financial situations.

Further Resources for Loan Studies

To deepen your understanding of borrowing concepts and financial problem-solving, it is essential to explore additional materials and resources. There are various platforms, textbooks, and online tools available that offer practical insights, exercises, and expert advice. These resources provide opportunities to refine your skills and ensure a comprehensive grasp of financial topics, from basic principles to more complex calculations.

Below are some recommended resources that can help enhance your knowledge:

Resource Type	Description	Recommended For
Online Financial Calculators	Interactive tools that help you calculate payment schedules, interest rates, and total repayment amounts based on different terms.	Practical application and quick calculation checks
Financial Textbooks	Comprehensive guides that cover all aspects of finance, including detailed explanations, formula derivations, and real-world examples.	In-depth study and theory building
Online Courses	Structured lessons and video tutorials from finance experts, focusing on various financial topics, including borrowing principles and strategies.	Learning through visual aids and structured lessons
Finance Forums	Discussion boards where finance professionals and students exchange ideas, tips, and resources related to borrowing practices and strategies.	Community-based learning and problem-solving

By utilizing these resources, you can reinforce your understanding and gain a broader perspective on borrowing topics. This will not only improve your ability to solve related problems but also enhance your overall financial literacy.