AP Calculus AB Exam Multiple Choice Answer Guide

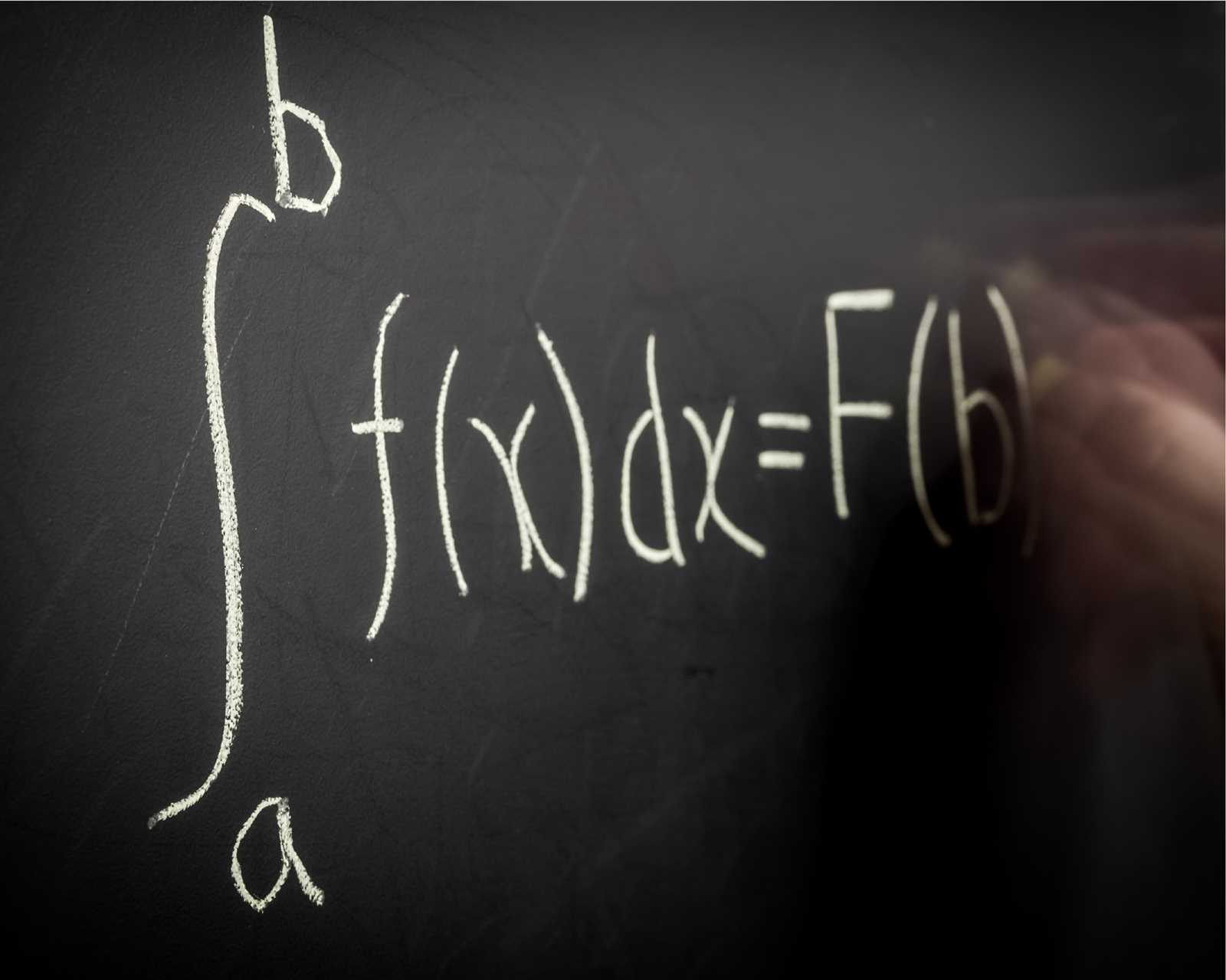
Preparing for a challenging test in advanced mathematics requires focused practice and a solid understanding of the fundamental principles. Mastering the key topics will help you not only solve problems more efficiently but also boost your confidence when facing timed assessments.

The process of solving problems under pressure can be overwhelming, especially when faced with complex questions. By breaking down each topic into smaller, manageable sections, you can approach each problem systematically and with greater ease. Whether it’s mastering differentiation, integration, or other advanced techniques, a strategic approach is essential for success.

Effective practice is crucial for enhancing both speed and accuracy. By reviewing various types of problems, focusing on the most frequently tested concepts, and honing problem-solving strategies, you can achieve a better grasp of the material and significantly improve your performance.

AP Mathematics Assessment Problem Solutions

When preparing for an advanced mathematics assessment, it’s essential to familiarize yourself with the types of questions you will encounter. These problems require not only understanding the material but also applying various techniques efficiently to find the correct solutions. Each question is designed to test your ability to analyze and work through mathematical concepts under timed conditions.

Key Strategies for Solving Problems

One of the most effective ways to approach such questions is by breaking them down step-by-step. Often, problems may seem complex at first, but with a methodical approach, you can identify the underlying patterns and apply the right strategy. Focus on understanding the core concepts such as limits, derivatives, integrals, and their applications to quickly pinpoint the necessary solution technique.

Problem Breakdown Example

Below is a table that outlines a typical problem from the test along with a breakdown of how to approach it. This will help you understand the thought process behind each step and how to recognize key elements in the question.

Problem Type	Step-by-Step Solution	Key Concepts Involved
Rate of Change	1. Identify the given function. 2. Differentiate the function. 3. Evaluate the derivative at the specified point.	Derivatives, Rate of Change
Area Under Curve	1. Set up the definite integral. 2. Integrate the function over the given limits. 3. Simplify the result.	Integration, Area Calculation

By practicing with a variety of problems and understanding the key principles involved, you will enhance your problem-solving skills and increase your chances of success in the assessment.

Key Concepts Tested in AP Mathematics

In any advanced mathematics assessment, certain fundamental concepts are emphasized to test your ability to apply theoretical knowledge to practical problems. Understanding these core topics is crucial for success, as they form the foundation for solving more complex questions. These key areas are designed to evaluate your understanding of how mathematical principles are interrelated and how they can be used in a variety of contexts.

Core Areas of Focus

Some of the primary topics that you will encounter in the assessment include rates of change, accumulation, and function analysis. Mastering these areas requires a deep understanding of both the conceptual framework and the problem-solving techniques that can be applied to real-world situations. Additionally, you will need to demonstrate your ability to perform various operations, such as differentiation and integration, to solve problems effectively.

Overview of Key Topics

The table below highlights some of the key concepts typically tested, along with a brief description of each. Familiarizing yourself with these concepts will provide a strong foundation for tackling related problems.

Concept	Description
Limits	Understanding the behavior of functions as they approach certain values, a critical concept for analyzing continuous functions.
Derivatives	Determining the rate of change of a function, essential for solving problems related to motion, growth, and optimization.
Integrals	Calculating the accumulated value of a function over an interval, widely used for finding areas under curves and solving real-world problems.
Fundamental Theorem of Calculus	Connecting derivatives and integrals, which provides the foundation for solving complex problems involving both rates of change and accumulation.

By mastering these core concepts, you will be well-equipped to tackle a variety of problems and perform well on the assessment.

How to Approach Multiple Choice Questions

When tackling timed assessments, the ability to effectively handle a variety of question types is essential. Multiple option questions are designed to test not only your knowledge of key topics but also your ability to think critically and manage time efficiently. A systematic approach to these types of questions can help you avoid common mistakes and maximize your score.

Read Each Question Carefully

The first step in answering any question is to read it thoroughly. Often, key information or subtle details can make the difference between a correct and incorrect choice. Pay attention to any qualifiers like “always,” “never,” or “except,” as they can change the meaning of the question entirely. Understanding the question fully before jumping to the options will help you make a more informed decision.

Eliminate Incorrect Options

Once you have read the question and understood what it is asking, begin by eliminating clearly incorrect options. This strategy narrows down your choices and increases your chances of selecting the correct answer. If you are unsure about the correct choice, process of elimination can often lead you to the right answer by removing distractors.

By approaching questions in a structured way, you ensure that you are considering all relevant information and making the most logical choices based on your understanding of the material.

Common Pitfalls to Avoid in Mathematics Assessments

When preparing for any advanced mathematics test, it’s easy to fall into common traps that can negatively impact your performance. These pitfalls often arise from misunderstanding key concepts, rushing through questions, or misapplying mathematical techniques. By being aware of these common mistakes, you can avoid them and approach problems more effectively during the assessment.

Typical Mistakes to Watch For

Below are some of the most frequent errors students make during assessments, along with tips on how to avoid them:

• Misinterpreting the Question: Always read the question carefully and understand what is being asked. Avoid rushing into a solution without fully grasping the problem.
• Skipping Steps: While it may seem like a time-saver, skipping steps in calculations can lead to errors. Always show your work and check your steps when possible.
• Incorrectly Applying Formulas: Make sure you are using the correct formula for the problem. Double-check whether you are solving for what is being asked, not just plugging numbers into the wrong equation.
• Overlooking Units or Limits: Pay attention to units of measurement and limits of integration or differentiation. Small details like this can change the final answer significantly.
• Relying Too Much on Guessing: While process of elimination can be helpful, relying too heavily on guessing without a clear strategy can cost valuable points. Take time to analyze the problem first.

How to Minimize These Errors

In order to avoid these pitfalls, you need to adopt a careful, deliberate approach during your preparation and when answering questions:

1. Practice Regularly: Frequent practice with problems of varying difficulty helps you identify areas where you are prone to mistakes and improve your accuracy.
2. Review Your Work: Always revisit your calculations before submitting your responses. This helps catch any simple errors you might have overlooked initially.
3. Focus on Understanding: Rather than memorizing formulas and procedures, focus on understanding the underlying concepts. This will help you apply techniques more accurately under pressure.

By being mindful of these common mistakes and adopting a more thoughtful approach to problem-solving, you can increase your chances of success and avoid unnecessary errors during the test.

Best Study Resources for AP Mathematics

Preparing for a rigorous mathematics assessment requires the right tools and materials to ensure you are fully equipped to succeed. Whether you’re a visual learner, someone who prefers hands-on practice, or someone who benefits from in-depth explanations, selecting the best study resources can significantly enhance your understanding of key concepts. There are a variety of resources available that cater to different learning styles and needs.

Essential Resources for Effective Studying

From textbooks and online courses to interactive problem solvers, the following study tools are among the best for mastering the material covered in the test. Each resource offers unique features designed to deepen your knowledge and prepare you for the types of questions you will encounter.

Top Study Materials Overview

Resource	Description	Benefits
Official AP Study Guide	Published by the College Board, this guide provides a comprehensive review of topics and practice questions.	Authentic practice materials, overview of key concepts, insights into exam structure.
Khan Academy	An online platform offering video lessons, practice exercises, and step-by-step explanations.	Free, accessible learning, visual and interactive content, personalized practice.
AP Classroom Resources	Tools provided by AP teachers, including practice questions and personalized progress tracking.	Direct access to exam-specific practice, real-time feedback on progress.
Practice Test Books	Books like those from Princeton Review and Barron’s that offer extensive practice tests.	Realistic practice tests, strategies for improving performance under timed conditions.
Online Tutoring Services	Platforms such as Chegg or Wyzant offer personalized tutoring for areas of difficulty.	Expert guidance, personalized help on challenging topics, flexible scheduling.

By combining these resources in your study plan, you will be able to tackle each topic confidently and be well-prepared for the challenges of the test. The key to success is consistent practice and utilizing a range of materials to reinforce your understanding.

Time Management Strategies for the Test

Efficiently managing your time during a high-pressure assessment is crucial for success. The ability to allocate the right amount of time to each question, while avoiding unnecessary delays, can make a significant difference in your performance. Developing strong time management skills allows you to confidently approach each section, ensuring you have sufficient time to review your work and address any challenging questions.

Key Time Management Tips

Here are several strategies to help you maximize your time and approach the assessment methodically:

• Know the Time Limits: Understand the overall time available for the assessment and the number of questions you need to answer. This will help you allocate time for each section and avoid rushing at the end.
• Prioritize Easier Questions: Quickly identify questions you find easiest and start with them. This allows you to build confidence and secure easy points early on.
• Don’t Get Stuck: If you encounter a particularly challenging question, move on and return to it later if time allows. Getting stuck can waste valuable minutes.
• Set Time Limits for Each Section: Break the test into manageable segments, and set a timer for each section to ensure you’re staying on track.
• Review Your Work: If time permits, leave a few minutes at the end to review your answers. This allows you to catch simple mistakes and refine your responses.

Planning Your Approach

To effectively manage your time, consider the following approach:

1. Start with a Quick Overview: When you first receive the test, scan through all the questions to get a sense of the difficulty and the amount of time you’ll need for each section.
2. Divide and Conquer: Break the test into smaller sections and tackle each one within a predetermined time frame. This will help prevent you from spending too much time on any single question.
3. Use the Process of Elimination: For questions you’re unsure about, use the process of elimination to narrow down the options. This saves time and increases your chances of selecting the correct response.

By applying these strategies and practicing under timed conditions, you’ll develop a solid approach to time management, ensuring that you make the most of the available time and maximize your chances of success.

Understanding the Grading Scale

Understanding the scoring system of an advanced mathematics assessment is crucial for gauging your performance and setting realistic goals. The grading scale provides a clear breakdown of how your answers are evaluated and how scores are distributed across different sections. Familiarity with the grading criteria can help you focus your study efforts on the areas that will have the greatest impact on your final score.

Components of the Grading System

The overall score for the test is calculated based on two primary components: the number of correct responses and the weighting of each section. It’s important to know how each part contributes to the final grade.

• Correct Responses: Each correct answer adds to your score. The more accurate responses you provide, the higher your total score will be.
• Section Weighting: The different sections of the assessment are weighted differently. Some sections may contribute more points to your final score, so it’s important to allocate time and focus accordingly.
• Penalty for Incorrect Answers: Some scoring systems include penalties for incorrect answers, while others only penalize unanswered questions. Understanding how the system works can help you decide whether to guess or leave a question blank.

Score Breakdown and Interpretation

Here is an overview of how your score is typically broken down and interpreted:

1. Raw Score: This is the total number of correct responses you provide across all sections. This score is then adjusted based on the weighting of each section.
2. Scaled Score: The raw score is converted into a scaled score, which accounts for the overall difficulty of the assessment. This score provides a more accurate representation of your performance compared to others taking the same test.
3. Final Score: The final score is the result of the scaled score, and this is typically reported as a number between 1 and 5. A higher score indicates stronger performance and a better grasp of the material.

By understanding how the grading system works, you can better focus your efforts during preparation and approach the test with a clear strategy for maximizing your score.

Reviewing Important Formulas for the Test

Mastering key formulas is essential for success in any advanced mathematics assessment. These formulas serve as the foundation for solving complex problems efficiently and accurately. A thorough understanding and quick recall of important equations will allow you to navigate through questions with confidence and precision. In this section, we will review the most critical formulas that you should be familiar with before taking the test.

Core Formulas to Remember

Here are some of the most commonly tested formulas that are crucial for solving problems related to limits, derivatives, integrals, and other fundamental concepts:

• Power Rule for Derivatives: f'(x) = n * x^(n-1) – This rule is used for differentiating power functions.
• Product Rule: (fg)’ = f’g + fg’ – This rule applies when differentiating the product of two functions.
• Quotient Rule: (f/g)’ = (f’g – fg’) / g^2 – Used to differentiate the quotient of two functions.
• Chain Rule: (f(g(x)))’ = f'(g(x)) * g'(x) – Essential for differentiating composite functions.
• Fundamental Theorem of Calculus: ∫[a,b] f(x) dx = F(b) – F(a) – This connects the process of differentiation and integration.
• Area Under a Curve: A = ∫[a,b] f(x) dx – The integral of a function represents the area under the curve between the given limits.
• Integration by Parts: ∫u dv = uv – ∫v du – A method for integrating the product of two functions.
• Sum and Difference Rules: (f ± g)’ = f’ ± g’ – Used for finding the derivative of sums or differences of functions.

Application of Formulas in Problem Solving

Simply memorizing formulas is not enough. To perform well, you need to practice applying these formulas to solve real-world problems. This is where the true value of these equations lies. It’s important to review problems from different categories and apply the relevant formula in each scenario. Regular practice will help solidify your understanding and improve your ability to use formulas under time constraints.

Familiarity with these essential formulas will give you the tools you need to approach the test with confidence. Review them regularly and incorporate them into your practice to ensure you’re fully prepared for any challenge that comes your way.

How to Interpret Test Question Phrasing

Understanding how questions are worded is an essential skill for success in any advanced assessment. The way a question is phrased can sometimes be tricky, and misinterpreting it can lead to unnecessary mistakes. It’s important to recognize the key terms and instructions in each question to ensure you’re answering what is being asked. In this section, we’ll discuss how to interpret common types of phrasing to help you navigate questions with confidence and accuracy.

Key Phrasing Tips

Different types of questions may have distinct phrasings that require specific attention. Here are some tips for interpreting the language used in questions:

• Look for Action Words: Words like “determine,” “find,” “calculate,” or “evaluate” provide clues about what type of response is expected. These terms tell you whether you should solve for a value, analyze a function, or perform a specific operation.
• Understand Conditional Statements: Be aware of terms like “if,” “when,” or “given that.” These words usually introduce assumptions or constraints that will impact your approach to solving the problem.
• Focus on Key Details: Pay attention to small but important details such as limits, boundaries, and variables mentioned in the question. These specifics will guide your method of solving.
• Recognize Common Mathematical Terms: Terms like “increase,” “decrease,” “rate of change,” or “area” all suggest different types of mathematical operations and concepts. Understanding these can help you quickly determine the appropriate method for solving.
• Beware of Negative Phrasing: Occasionally, questions may be phrased in a way that involves negatives or opposites, such as “not” or “exclude.” Be sure to read carefully to avoid making the opposite mistake.

Common Question Formats

Different question types may have specific wording that you need to interpret correctly. Some common formats include:

• Multiple-Parts Questions: These questions may include phrases like “which of the following,” followed by several options. The challenge is to identify which set of conditions applies to the problem, rather than just selecting one answer.
• Context-Based Problems: Often, a scenario is presented that requires you to apply theoretical knowledge to a real-world situation. In these cases, understanding the context is crucial for choosing the right mathematical concept to apply.
• Graph-Related Queries: Questions that ask about the behavior of a graph or its properties often use phrasing like “which of the following represents the graph of.” It’s important to focus on terms like slope, intercept, and asymptote to interpret the graph correctly.

By learning to recognize and interpret the various types of phrasing used in questions, you can avoid common pitfalls and answer more efficiently. This skill, combined with thorough practice, will significantly improve your ability to approach and solve problems with confidence.

Practice Questions for AP Calculus AB

One of the most effective ways to prepare for any advanced mathematical assessment is by practicing sample questions. Working through a variety of problems allows you to familiarize yourself with the format, identify key concepts, and refine your problem-solving techniques. In this section, we will explore some practice questions that cover the essential topics typically encountered in the test. These questions are designed to help you hone your skills and boost your confidence.

Sample Problem 1: Derivative and Rate of Change

Given the function f(x) = 3x² + 5x – 4, determine the derivative of the function and interpret its meaning in the context of a rate of change.

• Step 1: Apply the power rule to differentiate the function.
• Step 2: Interpret the result as the rate of change of the function at any point on the curve.

Sample Problem 2: Integration and Area Under the Curve

Find the area under the curve of the function f(x) = x³ – 2x + 1 from x = 1 to x = 3 using definite integration.

• Step 1: Set up the definite integral.
• Step 2: Solve the integral and interpret the result as the area between the function and the x-axis over the given interval.

Sample Problem 3: Application of the Mean Value Theorem

Given the function f(x) = sin(x) on the interval [0, π], use the Mean Value Theorem to find the value of c that satisfies the conditions of the theorem.

• Step 1: Apply the Mean Value Theorem formula.
• Step 2: Solve for c in the interval [0, π].

These practice questions cover a range of topics you’ll encounter in the test. By working through these types of problems, you will develop a deeper understanding of the material and become more proficient in applying mathematical techniques to solve complex problems. Make sure to review each problem carefully and practice regularly to ensure success.

Tips for Solving Limits Problems Efficiently

When tackling limit problems, efficiency is key. The ability to quickly identify the correct method and apply it effectively can make a significant difference in solving problems accurately and on time. In this section, we will discuss strategies for approaching limits problems, from recognizing common patterns to utilizing shortcuts that will help you streamline your solutions.

Understand the Basic Rules

Before diving into more complex scenarios, make sure you are familiar with the fundamental rules and properties of limits. Some of the most important include:

• Direct Substitution: If the function is continuous at a point, simply substitute the value of x into the function to find the limit.
• Limits of Sums and Differences: The limit of a sum or difference is the sum or difference of the individual limits.
• Limits of Products and Quotients: Apply the rules for multiplying or dividing limits when dealing with product or quotient functions.

Recognize Indeterminate Forms

When you encounter indeterminate forms, such as 0/0 or ∞/∞, it’s crucial to identify the situation early so you can apply the right technique to resolve it. Common methods include:

• L’Hôpital’s Rule: If you encounter a 0/0 or ∞/∞ form, apply L’Hôpital’s Rule by differentiating the numerator and denominator separately until you can resolve the limit.
• Factoring: Factor the numerator and denominator and cancel out common terms to simplify the expression before taking the limit.
• Rationalizing: For limits involving square roots, consider rationalizing the numerator or denominator to simplify the expression.

Work with Graphical Interpretation

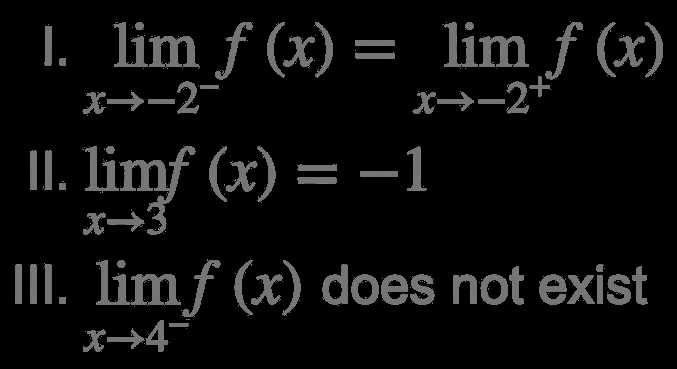
When you’re unsure of a limit, sometimes graphing the function can provide helpful insight. Look for trends in the function’s behavior as it approaches the point of interest. This can often reveal whether the limit exists, whether there is an asymptote, or whether the function approaches infinity.

Practice with a Variety of Functions

As with any mathematical concept, practice is essential. Work through problems involving polynomial functions, rational functions, exponential functions, and trigonometric functions to get comfortable with applying the various techniques. Familiarity with these different types of functions will help you recognize which method to use and how to proceed efficiently.

By mastering these techniques, you will be able to solve limit problems quickly and accurately, increasing your confidence in applying them to more complex problems. Keep practicing and refining your strategies, and you’ll see improvement in your efficiency and problem-solving skills.

Mastering Derivatives for AP Calculus

Understanding derivatives is a crucial skill when preparing for advanced mathematics assessments. By mastering the principles and techniques behind derivatives, you will be able to tackle a wide range of problems effectively. This section focuses on building a strong foundation in derivatives, covering essential concepts and strategies to help you excel in related questions.

Fundamental Rules of Differentiation

Start by mastering the core rules of differentiation, which are the building blocks for more complex problems:

• Power Rule: For any function of the form f(x) = x^n, the derivative is f'(x) = n * x^(n-1).
• Product Rule: When differentiating the product of two functions, (f * g)’ = f’ * g + f * g’.
• Quotient Rule: For the quotient of two functions, (f / g)’ = (f’ * g – f * g’) / g^2.
• Chain Rule: When differentiating a composition of functions, apply (f(g(x)))’ = f'(g(x)) * g'(x).

Applications of Derivatives

Once you’ve mastered the basic rules, apply them to solve real-world problems. Derivatives are used to find rates of change, slopes of tangents, and to analyze functions for critical points, concavity, and inflection points. These applications are vital when solving more complex problems involving optimization and motion.

• Critical Points: Find where the first derivative equals zero or does not exist to locate maximum and minimum values of a function.
• Concavity and Inflection Points: The second derivative helps determine the concavity of a function and where it changes from concave up to concave down.
• Optimization: Use derivatives to solve problems involving maximum or minimum values, such as maximizing profit or minimizing cost.

By understanding these fundamental rules and their applications, you’ll be equipped to handle a wide variety of derivative-related questions. Practice solving problems that involve both basic differentiation and its applications to strengthen your understanding and efficiency in solving them during assessments.

How to Tackle Integration Questions

When approaching questions that involve finding the integral of a function, it’s essential to break down the process into manageable steps. Integration is a key concept in advanced mathematics that involves calculating the area under curves, determining accumulated quantities, and solving a variety of problems across multiple contexts. By understanding the basic methods and applying strategies effectively, you can simplify complex problems and find solutions with greater confidence.

Essential Techniques for Integration

To approach integration problems efficiently, start by mastering the fundamental techniques:

• Basic Antiderivatives: Recognize common functions and their corresponding integrals. For example, the integral of x^n is (x^(n+1)) / (n+1), and the integral of e^x is simply e^x.
• Substitution Method: Use substitution to simplify integrals that involve composite functions. Choose a substitution that makes the integral easier to solve.
• Integration by Parts: For integrals involving products of functions, apply the integration by parts formula: ∫u dv = uv – ∫v du.
• Partial Fractions: For rational functions, decompose the integrand into simpler fractions to make the integration process more straightforward.

Strategies for Problem Solving

Here are some strategies to help you effectively solve integration problems:

1. Identify the form: Examine the given function to identify its form and choose the appropriate method for integration. Look for common patterns such as polynomials, exponentials, trigonometric functions, or rational expressions.
2. Simplify the expression: Before integrating, simplify the integrand as much as possible. This may involve factoring, expanding, or using algebraic manipulations to make the integral more manageable.
3. Check for bounds: If the problem involves definite integration, always keep track of the limits of integration. Evaluate the integral at the bounds to find the area or accumulated quantity.
4. Practice, Practice, Practice: Regular practice with various types of integration problems will help you become more familiar with the different methods and strategies. The more problems you solve, the quicker and more accurate you’ll become.

By mastering these methods and applying them with strategic thinking, you’ll improve your ability to handle integration questions and strengthen your mathematical skills for a wide range of problem types.

Approaching Differential Equations on the Exam

Solving differential equations can seem daunting at first, but with the right approach, these problems can become much more manageable. Differential equations involve relationships between functions and their derivatives, and solving them often requires a systematic strategy to identify the appropriate method. Whether the equation is separable, linear, or requires some form of integration, understanding the key techniques will help you navigate these questions with confidence.

Key Strategies for Solving Differential Equations

To tackle differential equations effectively, consider the following strategies:

• Identify the type of equation: The first step is recognizing the type of differential equation you are dealing with. Common types include separable equations, linear equations, and those that can be solved using integrating factors.
• Separation of variables: For separable equations, the goal is to rewrite the equation so that all terms involving y are on one side and all terms involving x are on the other. After separation, integrate both sides to find the general solution.
• Linear equations: Linear first-order equations can be solved using an integrating factor. Identify the integrating factor based on the form of the equation and multiply through to simplify it.
• Use substitution if necessary: Some differential equations may require substitution methods, such as using u = y/x, to simplify and solve the equation more efficiently.

Steps for Solving Differential Equations

Follow these steps to approach solving differential equations:

1. Rearrange the equation: Begin by isolating the derivative on one side of the equation. If the equation is linear, rewrite it in standard form to identify the correct method for solving.
2. Choose the appropriate technique: Once the equation is in the right form, select the method that applies. For separable equations, use separation of variables. For linear equations, use the integrating factor method.
3. Integrate both sides: After applying the appropriate technique, integrate both sides of the equation with respect to the independent variable. Don’t forget to add the constant of integration when solving indefinite integrals.
4. Solve for the function: After integration, solve for the dependent variable. If the equation is a definite one, substitute the given initial conditions to find any constants.
5. Check the solution: Verify your solution by substituting it back into the original differential equation to ensure it satisfies the equation.

By applying these strategies, you’ll be able to approach differential equations on the test with greater clarity and efficiency. Consistent practice and familiarity with the various methods will help you solve these problems confidently and accurately under time constraints.

Preparing for the AP Exam Calculator Section

In many assessments, the use of a calculator can significantly enhance your ability to solve complex problems quickly and accurately. The calculator section of the test is designed to assess your ability to use technological tools to aid in problem-solving, especially when dealing with functions, graphs, and numerical methods that would be time-consuming or difficult to compute by hand. Proper preparation for this section involves understanding not only the calculator’s capabilities but also how to leverage them effectively during the test.

First and foremost, familiarize yourself with the specific calculator model that is allowed on the test. While most scientific and graphing calculators are acceptable, understanding the functions of your specific model will save you valuable time during the assessment. This includes knowing how to graph functions, compute derivatives and integrals, and utilize built-in features for solving equations or evaluating limits.

In addition to mastering your calculator’s features, practice using it in conjunction with problem-solving strategies. For example, graphing a function before analyzing its behavior can provide important insights, while using numerical integration to approximate areas under curves can help solve otherwise challenging problems. Time spent becoming efficient with your calculator will translate into greater accuracy and speed on the day of the test.

Remember, the key is to strike a balance between manual techniques and calculator use. The calculator should supplement your understanding, not replace it. Being able to interpret the results generated by your calculator and understanding the underlying concepts is critical to performing well.

Post-Exam: Understanding Your Results

After completing the assessment, the next step is to carefully review your performance and understand the results. Interpreting your scores is not just about knowing your total, but also analyzing where you excelled and where improvement may be needed. This process allows you to gain valuable insights into your strengths and weaknesses, which can guide your future studies and help you refine your problem-solving techniques.

One key aspect of understanding your results is reviewing the breakdown of your performance. Most assessments provide a detailed score report that highlights how well you did in different areas. Pay close attention to these categories, as they reflect the types of skills and concepts that were tested. Identifying areas where you scored lower can help you target your review for future tests or help in improving your understanding of certain topics.

Additionally, it’s important to understand how your score compares to the overall performance of other participants. This context can help you gauge where you stand relative to your peers. If you scored well, celebrate your achievements, but also consider what you can improve upon. If your score wasn’t as high as you’d hoped, use it as an opportunity to develop a deeper understanding of the material and to focus on the areas that need more attention.

Remember, your results should be seen as a tool for growth. Rather than focusing solely on the outcome, use the feedback to develop a stronger grasp of the concepts and strategies that are essential for success in future assessments or in practical applications. It’s not the score itself, but the lessons learned through the review process that will help you succeed in the long run.