Flvs Geometry Segment 2 Exam Answer Key

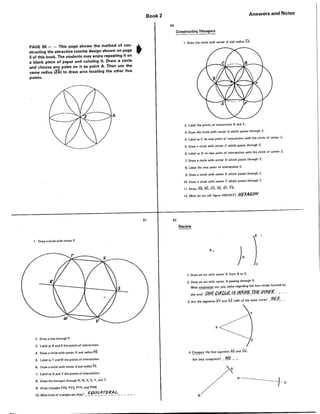
In the second part of the curriculum, students are introduced to a series of mathematical concepts that test their ability to reason and solve problems. This section emphasizes the application of different techniques to solve real-world challenges and theoretical puzzles. Mastering these skills is crucial for success in future coursework and exams.

To excel in this phase, it’s important to focus on understanding the fundamental principles behind the problems, not just memorizing formulas. The challenges presented require a logical approach, as well as attention to detail. By practicing with various problems, students can develop the skills necessary to approach any question with confidence and precision.

Throughout this section, critical thinking plays a significant role in finding solutions. By identifying patterns and applying problem-solving strategies, learners can significantly improve their performance. With the right preparation, students can navigate through complex problems and demonstrate their knowledge effectively.

Flvs Geometry Segment 2 Exam Answer Key

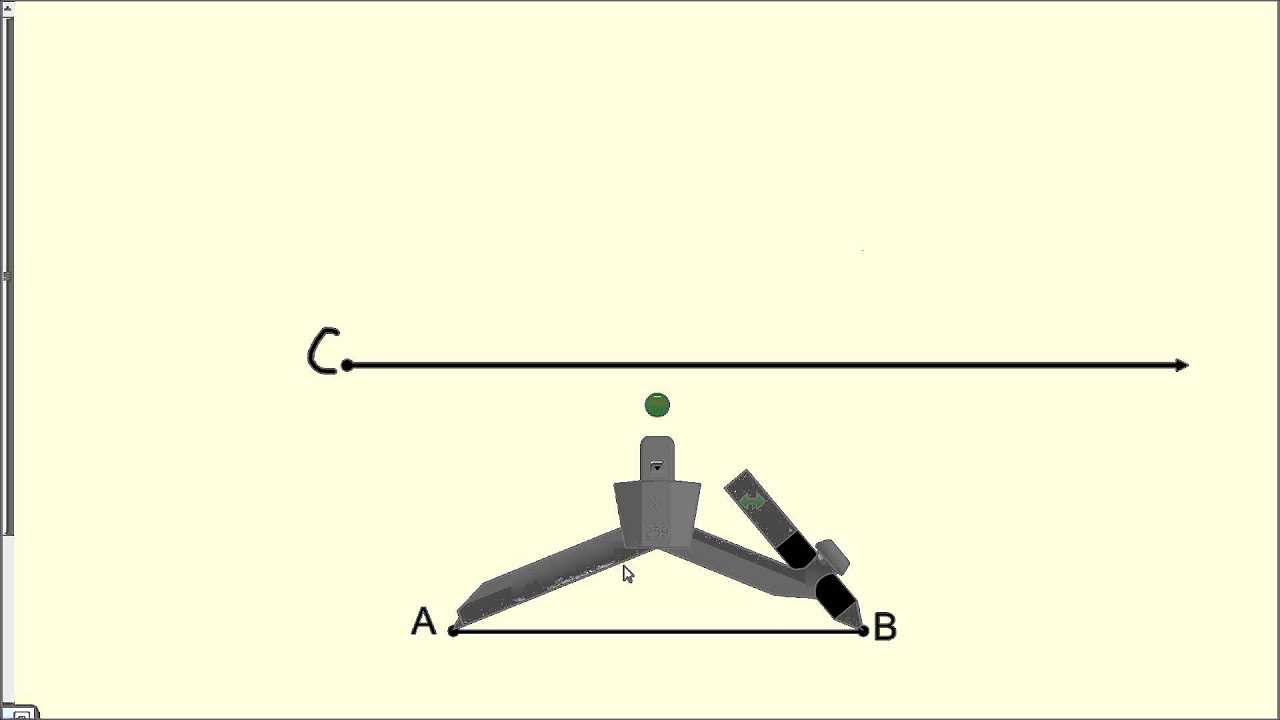
This section offers detailed solutions and step-by-step guidance for the challenges presented in the second phase of the mathematical course. Students will find useful resources to help navigate through complex problems and build a deeper understanding of the required concepts. By examining each problem and its corresponding solution, learners can enhance their grasp of the material and improve their performance.

Approaching Complex Problems

When tackling these types of questions, it’s essential to apply logical reasoning and problem-solving techniques. Each challenge is designed to test various aspects of knowledge, and solutions often involve breaking down problems into smaller, manageable steps. By practicing these techniques, students can boost their confidence and ability to tackle even the most challenging scenarios.

Reviewing Solutions for Better Understanding

Reviewing the solutions after attempting the problems is a valuable practice. It helps identify any areas where improvement is needed and allows for the reinforcement of key concepts. The following table summarizes common questions and their solutions to assist students in reinforcing their understanding:

Problem	Solution
Calculate the area of a circle with radius 5	Area = π * r² = 3.14 * 5² = 78.5
Find the volume of a cylinder with radius 3 and height 8	Volume = π * r² * h = 3.14 * 3² * 8 = 226.08
Solve for x: 2x + 5 = 15	x = 5
Determine the perimeter of a rectangle with sides 7 and 10	Perimeter = 2 * (7 + 10) = 34

Overview of Geometry Segment 2 Exam

The second portion of the curriculum focuses on a variety of mathematical concepts aimed at testing your ability to apply learned principles. This section is designed to challenge your problem-solving skills through both theoretical questions and practical applications. You will encounter a mix of topics that require a deeper understanding and the ability to use various techniques to solve different types of problems.

Success in this section depends on your ability to break down complex questions into simpler components and apply the correct formulas or strategies. The variety of problems ensures that students not only memorize concepts but also understand how to use them in diverse contexts. It is essential to practice extensively to develop the necessary skills and build confidence in tackling the problems efficiently.

Key Topics Covered in Segment 2

This portion of the curriculum introduces essential mathematical concepts, each designed to build upon previously learned material. The content explores various methods for solving problems involving shapes, sizes, and spatial relationships. Understanding these topics is critical for progressing in the subject, as they serve as the foundation for more advanced studies.

Understanding Spatial Relationships

One of the key areas in this section involves examining how different objects and figures relate to each other in space. Students will explore the properties of angles, lines, and planes, and learn how to calculate the measurements of these components. These fundamental concepts are integral to solving problems involving various shapes and understanding their interactions.

Application of Formulas and Theorems

The ability to apply formulas and theorems accurately is a core skill in this section. Learners will work with equations related to area, perimeter, and volume, among others. Familiarity with these formulas enables students to solve real-world problems and proves essential for achieving success in this phase of the course.

Understanding Exam Format and Structure

The structure of this assessment is carefully designed to evaluate your ability to apply the knowledge you’ve gained throughout the course. The test consists of different sections, each focusing on a specific set of skills and mathematical concepts. Understanding the layout and organization of the assessment will help you approach it with confidence and improve your chances of success.

Types of Questions

The assessment features a variety of question types, each testing different aspects of your understanding. These may include:

• Multiple Choice: Select the correct option from a list of choices.
• Short Answer: Provide a brief written response or calculation.
• Problem Solving: Work through a series of steps to find a solution to a complex problem.
• True/False: Determine the accuracy of a given statement based on your knowledge.

Time Allocation and Tips

Each section is allotted a specific amount of time, so it’s essential to manage your time effectively during the test. Here are a few tips:

1. Start with the questions you feel most confident about.
2. Don’t spend too much time on any single question. Move on if needed.
3. Double-check your work to avoid careless mistakes.
4. Use scratch paper for complex calculations or drawings.

How to Prepare for Geometry Segment 2

Effective preparation for this portion of the course involves a combination of reviewing foundational concepts, practicing problem-solving, and mastering key strategies. By focusing on these areas, you can approach the challenges with confidence and increase your likelihood of success. Planning ahead and organizing your study sessions is crucial to ensure thorough understanding and retention of the material.

Key Areas to Focus On

When preparing for this phase, concentrate on the following core areas:

• Understanding the Basics: Make sure you have a solid grasp of basic mathematical principles, including operations, properties of shapes, and measurement techniques.
• Practice with Formulas: Familiarize yourself with important formulas for calculating area, perimeter, volume, and other geometric properties.
• Problem-Solving Techniques: Work through a variety of practice problems to build your ability to apply concepts to real-world scenarios.
• Review of Theorems: Focus on key theorems that help solve more complex problems, such as properties of angles and parallel lines.

Study Strategies

To ensure effective preparation, follow these proven study methods:

1. Consistent Practice: Set aside time each day to review and solve practice problems. Regular practice helps reinforce concepts.
2. Break Down Complex Problems: Break larger problems into smaller, manageable steps to avoid feeling overwhelmed.
3. Use Additional Resources: Make use of online tutorials, study guides, and reference books to deepen your understanding of challenging topics.
4. Group Study: Consider studying with peers to share insights, clarify doubts, and practice problem-solving together.

Common Pitfalls in Geometry Exams

In this portion of the course, students often encounter specific challenges that can hinder their performance. These difficulties arise from a lack of understanding of key concepts, careless mistakes, or ineffective problem-solving strategies. Being aware of these common obstacles can help you avoid them and improve your results. By recognizing where errors tend to occur, you can adjust your approach and study habits accordingly.

One frequent issue is rushing through problems without carefully reading the instructions. Many students overlook important details, which can lead to incorrect calculations or missed steps. Another common pitfall is not fully understanding the application of formulas. It’s crucial to know when and how to use the right formula in different scenarios. Additionally, failing to double-check work can lead to simple mistakes that negatively impact the final score.

Finally, students often struggle with managing their time effectively. Spending too much time on a single question or section can prevent you from completing the entire assessment. Practice with timed mock problems can help improve time management skills and ensure you have enough time to address every part of the assessment.

Important Formulas for Segment 2 Exam

To succeed in this portion of the course, it is essential to be familiar with the key formulas that are frequently applied to solve problems. These mathematical expressions form the foundation of many questions and serve as the tools needed to calculate areas, volumes, angles, and other critical aspects of the material. Having a solid understanding of these formulas will enable you to approach problems with greater confidence and accuracy.

Area and Perimeter Formulas

One of the most fundamental areas of focus is the ability to calculate the area and perimeter of various shapes. Here are some key formulas:

• Area of a Rectangle: A = l × w (where l is length and w is width)
• Area of a Circle: A = π × r² (where r is the radius)
• Perimeter of a Rectangle: P = 2 × (l + w)
• Perimeter of a Square: P = 4 × s (where s is the side length)

Volume and Surface Area Formulas

Understanding how to find the volume and surface area of three-dimensional objects is another key aspect. These formulas are essential for solving problems related to solids:

• Volume of a Cube: V = s³ (where s is the side length)
• Volume of a Cylinder: V = π × r² × h (where r is radius and h is height)
• Surface Area of a Cylinder: SA = 2πr² + 2πrh
• Surface Area of a Sphere: SA = 4πr² (where r is the radius)

Tips for Improving Geometry Skills

Improving your mathematical abilities requires consistent practice, a solid understanding of core concepts, and effective problem-solving strategies. By focusing on specific techniques and methods, you can strengthen your skills and gain more confidence when facing challenges. Here are some helpful tips to help you sharpen your proficiency in this area.

Focus on Fundamental Concepts

A strong grasp of the basic principles is essential for mastering more complex topics. Make sure you understand the core concepts that underpin the subject, such as:

• Properties of shapes and figures
• Relationships between angles and lines
• Understanding geometric transformations
• Application of key formulas and theorems

Effective Practice Techniques

To build and reinforce your skills, consistent practice is crucial. Here are some methods to help you improve:

1. Solve a Variety of Problems: Work on a mix of simple and complex problems to ensure you’re ready for any question type.
2. Understand Mistakes: After practicing, go over your errors carefully. Understand why you made them and how to avoid them in the future.
3. Use Visual Aids: Draw diagrams or use physical models to visualize concepts, especially when dealing with spatial problems.
4. Set Time Limits: Practice solving problems within a set time to simulate test conditions and improve your time management skills.

Answer Key Insights for Segment 2

Understanding the solutions to various problems is an essential part of mastering any mathematical subject. By reviewing the correct responses and analyzing the methods used to arrive at them, students can deepen their understanding of the concepts involved. This approach not only helps reinforce correct techniques but also reveals common mistakes that can be avoided in future assessments.

Learning from the Correct Solutions

Carefully studying the solutions can provide valuable insights into how problems should be approached. For instance:

• Step-by-Step Process: Pay attention to how each problem is broken down into manageable steps, as this ensures clarity and accuracy in reaching the final result.
• Use of Formulas: Notice which formulas are used for different types of problems, and how they are applied correctly in context.
• Common Pitfalls: Identifying common errors in the solutions can help prevent similar mistakes in your own work.

Improving Through Practice

Repeatedly reviewing and solving problems, especially those you find challenging, is crucial for improving accuracy. The more you practice with similar problems and study the reasoning behind each solution, the better prepared you will be for future challenges. Additionally, practicing different types of questions ensures a well-rounded skill set and enhances problem-solving speed.

Step-by-Step Solutions for Common Problems

Breaking down complex problems into smaller, manageable steps is key to mastering any subject. By following a clear process, students can better understand how to approach each type of question and ensure that they arrive at the correct answer. Below are solutions to some of the most common types of problems that often appear in this area of study.

Solving Area and Perimeter Problems

When dealing with area and perimeter calculations, it’s essential to apply the right formula and follow each step carefully. Here’s a breakdown of how to approach these problems:

1. Identify the Shape: Determine which shape is being referenced (e.g., square, rectangle, triangle, circle).
2. Write the Formula: Use the correct formula for the shape. For example:
   • Area of a rectangle: A = length × width
   • Perimeter of a square: P = 4 × side length
3. Substitute Known Values: Plug in the known dimensions into the formula.
4. Perform Calculations: Carefully calculate the result, ensuring you follow order of operations when needed.
5. Double-Check Your Work: Verify that your units are consistent and that the correct formula was applied.

Solving Problems Involving Angles

When working with angles, understanding the relationships between them is crucial. Here’s a step-by-step guide to solving angle-related problems:

1. Understand Angle Relationships: Identify whether you are dealing with complementary, supplementary, or vertical angles.
2. Write Equations: For example, if two angles are supplementary, their sum equals 180°. Set up an equation: angle 1 + angle 2 = 180°.
3. Solve for the Unknown: Use algebraic methods to solve for the unknown angle, keeping the equation balanced.
4. Check Your Results: Verify that the angles satisfy the original relationship (e.g., the sum of complementary angles should be 90°).

By following these structured approaches to common problems, you can develop a clearer understanding of the material and improve your ability to solve similar questions accurately in the future.

How to Approach Geometry Word Problems

Word problems in mathematics can be challenging, especially when they involve concepts that require logical reasoning and the application of formulas. The key to solving these problems is breaking them down into smaller, more manageable parts. By carefully reading the problem, identifying the necessary information, and following a systematic approach, you can improve your ability to tackle these types of questions with confidence.

Step 1: Understand the Problem

The first step is to read the problem carefully, often more than once, to ensure you fully understand what is being asked. Pay attention to the key details and the relationships between different elements in the problem. For example:

• Identify the shapes or objects involved.
• Note any given measurements, such as lengths, angles, or areas.
• Understand the question being asked–what do you need to find?

Step 2: Plan Your Solution

Once you understand the problem, plan your approach. This typically involves selecting the appropriate formula or method to solve the problem. Some helpful steps include:

• Choose the Right Formula: For example, if the problem involves calculating the area of a triangle, recall the formula: Area = 1/2 × base × height.
• Set Up the Equation: Translate the problem into an equation using the information provided.
• Organize the Information: Write down any known values and what you need to find.

Step 3: Solve the Problem

Use the appropriate steps to solve for the unknown. Pay careful attention to units, ensuring consistency throughout your calculations. Double-check that you have applied the correct formula and methods. Lastly, ensure that the final answer makes sense in the context of the problem.

With practice, your ability to approach and solve word problems will improve, helping you become more comfortable with even the most complex scenarios.

Resources for Geometry Practice

To excel in any area of mathematics, consistent practice and access to helpful resources are essential. Whether you’re looking to reinforce your understanding of key concepts, improve problem-solving skills, or prepare for assessments, various tools can help you along the way. Below are some valuable resources that can aid in honing your skills and mastering the material.

Online Practice Platforms

Online platforms offer interactive practice problems, video tutorials, and explanations to enhance learning. Here are some popular ones:

• Khan Academy: Provides a wide range of lessons and exercises, catering to various levels of difficulty.
• Brilliant.org: Offers problem-solving challenges and guided lessons designed to deepen your understanding.
• IXL: Focuses on targeted practice with immediate feedback and explanations to help you track progress.
• Art of Problem Solving (AoPS): Known for offering challenging problems and an online community for learners to discuss and share strategies.

Textbooks and Workbooks

Traditional textbooks and workbooks continue to be reliable resources for structured learning. Here are some recommended materials:

• “The Art of Problem Solving” series: A well-regarded series that focuses on developing critical thinking and problem-solving skills.
• “Precalculus” by Michael Sullivan: Includes detailed explanations, examples, and practice problems related to mathematical concepts.
• “Practice Makes Perfect: Geometry”: A workbook filled with exercises and step-by-step solutions.

Study Groups and Forums

Joining a study group or participating in online forums can provide additional support and help with difficult problems:

• Reddit (r/learnmath): A community where learners can ask questions, share resources, and get advice on various math topics.
• Stack Exchange (Mathematics): A Q&A site where you can ask specific questions and find expert-level explanations.
• Discord Study Groups: Many study groups on Discord focus on mathematics, where you can get real-time help from peers and tutors.

By using these resources, you can significantly improve your skills and understanding, ensuring that you are well-prepared for any challenge that comes your way.

Strategies for Exam Time Management

Effectively managing time during assessments is crucial for performing well, especially when tackling complex questions within a limited period. Proper time management can help ensure that all sections are completed with enough time for review. By following a few structured approaches, you can optimize your performance and reduce stress on test day.

Tips for Efficient Time Allocation

One of the most important aspects of time management is distributing your available time wisely across different sections of the assessment. Here are some key strategies:

Strategy	Description
Prioritize Easy Questions	Start with questions you can answer quickly to build confidence and secure points early.
Set Time Limits per Section	Allocate a specific amount of time for each section based on its complexity and length.
Avoid Spending Too Much Time on One Question	If you’re stuck on a question, move on and return to it later with a fresh perspective.
Use Spare Time Wisely	If you finish early, review your work thoroughly rather than rushing through.

Maximizing Efficiency During the Test

In addition to allocating time properly, being mindful of how you use the time you have can make a big difference. Here are some techniques for maximizing efficiency during the assessment:

• Read Instructions Carefully: Misunderstanding instructions can waste valuable time. Ensure you know exactly what is being asked before starting.
• Stay Calm and Focused: Anxiety can waste time. Keep a steady pace and focus on one question at a time.
• Utilize All Available Resources: If calculators, scratch paper, or formula sheets are provided, make sure to use them to your advantage.

By implementing these strategies, you can make the most of the time you have during any test, reducing pressure and increasing your chances of success.

How to Review Incorrect Answers

After completing a test, reviewing incorrect responses is a crucial step in improving your understanding and avoiding similar mistakes in the future. By carefully analyzing errors, you can pinpoint areas where you need more practice or clarification. This process helps reinforce the material and strengthens your problem-solving skills.

Steps to Analyze Mistakes

To effectively review incorrect answers, it’s important to follow a structured approach. Here are some key steps to guide you through the process:

Step	Description
Identify the Mistake	Carefully examine each incorrect response and identify the exact point where the error occurred. Was it a calculation mistake, misunderstanding of the concept, or a misinterpretation of the question?
Understand Why it’s Wrong	Once you’ve identified the mistake, try to understand why your answer was incorrect. Was the formula applied incorrectly, or did you overlook important details?
Review the Correct Method	Go over the correct procedure or concept for the problem. Understand the logic behind the solution, and practice with similar problems to reinforce the concept.
Apply the Correct Approach	After understanding where you went wrong, try to solve similar problems on your own using the correct approach. This practice will help solidify the right techniques in your mind.

Common Mistakes to Look For

When reviewing mistakes, pay special attention to some of the most common errors that often occur during assessments. These include:

• Rushing Through Problems: Hasty work often leads to simple calculation errors or missed steps in the problem-solving process.
• Misreading Instructions: Sometimes, incorrect answers arise from misunderstanding the requirements of the question. Double-check the instructions before proceeding.
• Forgetting to Double-Check: Not reviewing your final answer can result in overlooked mistakes, especially with complex questions.

By thoroughly reviewing your mistakes and taking time to understand where and why you went wrong, you can improve your performance on future assessments and ensure greater success in your studies.

Understanding Proofs in Segment 2

In this section, students are introduced to the fundamental concept of logical reasoning through structured arguments. Proofs form the backbone of mathematical arguments, where conclusions are drawn based on previously established facts, axioms, and logical deductions. Mastering this skill is essential for understanding complex problems and demonstrating the validity of statements in a formal way.

To successfully navigate proofs, it’s important to approach them step by step. Proofs require a clear, systematic structure, and often begin with known facts or assumptions and build towards the conclusion using logical steps. This methodical approach ensures that every argument is sound and that each step follows logically from the previous one.

Common types of reasoning used in proofs include direct proofs, where the statement is proven by straightforward logic, and indirect proofs, which involve assuming the opposite of the statement and showing that this leads to a contradiction. Understanding both approaches and knowing when to apply them is crucial for tackling proof-based problems.

Additionally, it is important to become familiar with key geometric properties and theorems that are often used as building blocks in proofs. The more you understand these foundational concepts, the easier it will be to recognize how they apply to different problems. Practice with a variety of problems will also help solidify your understanding and improve your ability to construct valid, coherent arguments.

Best Study Materials for Geometry Exams

Effective preparation for mathematical assessments requires access to high-quality resources that offer both depth and clarity. The right study materials can make the difference in understanding complex concepts and performing well under pressure. A combination of textbooks, online resources, practice exercises, and review guides can help solidify knowledge and boost confidence.

Start by using textbooks that cover the fundamental principles and provide plenty of examples. Textbooks are often the most reliable source of information as they offer step-by-step explanations and practice problems that progress in difficulty. Look for editions with comprehensive answer explanations to help clarify any misunderstandings.

Online Resources and Practice Tools

In addition to traditional textbooks, the internet is full of helpful materials, including interactive tools, video lessons, and forums where students can ask questions and share insights. Websites offering practice problems, quizzes, and mock tests are invaluable in reinforcing concepts and helping students gauge their progress.

• Khan Academy: Provides free video tutorials and practice exercises, perfect for understanding difficult concepts at your own pace.
• Wolfram Alpha: An online tool that helps solve problems step by step, providing detailed explanations of solutions.
• Quizlet: Offers flashcards and practice quizzes that are great for memorization and quick reviews.

Study Guides and Review Books

Study guides and review books are essential tools for focused revision. These guides often highlight the most important topics, offering summaries, tips, and strategies for tackling specific types of questions. Many review books also include practice tests that simulate actual conditions, which helps reduce test anxiety.

• Barron’s Study Guides: Known for detailed summaries and practice questions, perfect for self-study.
• Princeton Review: Offers concise guides with expert strategies and practice tests.

Combining these resources with consistent practice will help you become familiar with all the material and refine your problem-solving skills. Use a variety of materials to ensure a comprehensive understanding and readiness for any challenge that may arise during your studies.

How to Stay Calm During the Exam

Maintaining composure during a challenging assessment is crucial to perform at your best. Anxiety and stress can cloud your judgment and make it harder to think clearly. However, there are several strategies that can help you stay calm and focused, ensuring that you approach each question with clarity and confidence.

One of the most effective ways to stay calm is through deep breathing techniques. Taking slow, deliberate breaths can help reduce tension and lower your heart rate, which in turn helps keep your mind focused. If you feel anxious, pause for a moment, close your eyes, and breathe deeply to regain composure.

Preparation is also key to feeling at ease during the test. When you’re well-prepared, you’ll have confidence in your abilities. Make sure to review the material thoroughly beforehand, but also ensure you get plenty of rest the night before. Being well-rested helps your brain function more effectively, which can reduce stress levels.

Time management is another essential aspect of staying calm. Read through the entire assessment before you begin, and decide how long you’ll spend on each section. Prioritize questions based on your strengths and avoid getting bogged down on particularly difficult ones. If you’re stuck, move on and come back to the tricky questions later.

Lastly, remember that it’s just one test. It doesn’t define your ability or worth. Keep a positive mindset and remind yourself that you have prepared well. With the right mindset, you’ll be able to handle the pressure and approach the assessment with a calm, clear head.

Final Review Checklist for Segment 2

Before tackling any important assessment, a final review is essential to ensure you’re fully prepared. This checklist is designed to help you systematically go over the key concepts, problems, and strategies that will be tested. By following this guide, you can boost your confidence and make sure that no important detail is overlooked.

1. Review Core Concepts

Go through all the fundamental concepts you’ve studied. Make sure you understand the basic principles and can apply them to various types of problems. Focus on:

• Formulas: Ensure you’ve memorized key formulas and know how to apply them correctly.
• Theorems: Understand the proof and application of major theorems.
• Common Techniques: Be able to recognize patterns in problems and identify which methods or strategies to use.

2. Practice with Sample Problems

Test your skills by solving a range of problems. Be sure to include both easy and challenging examples to ensure a well-rounded review. Pay attention to:

• Accuracy: Double-check your answers for any calculation mistakes.
• Time Management: Practice solving problems within a set time frame to improve speed.
• Problem Types: Make sure to cover all types of problems that may appear.

3. Plan for Test Day

In addition to reviewing content, it’s important to prepare mentally and logistically. Make sure you’re ready for the actual test by considering the following:

• Sleep: Get a good night’s rest before the test to ensure you’re alert and focused.
• Materials: Confirm that you have everything you need, such as a calculator, pencils, and a ruler.
• Mindset: Approach the assessment with a positive attitude. Stay calm, stay confident, and remember that preparation is key.

By following this checklist, you’ll be able to focus on the most important aspects and enter the assessment feeling prepared and confident. Take your time during the final review, and make sure you’ve covered all the essentials before test day.