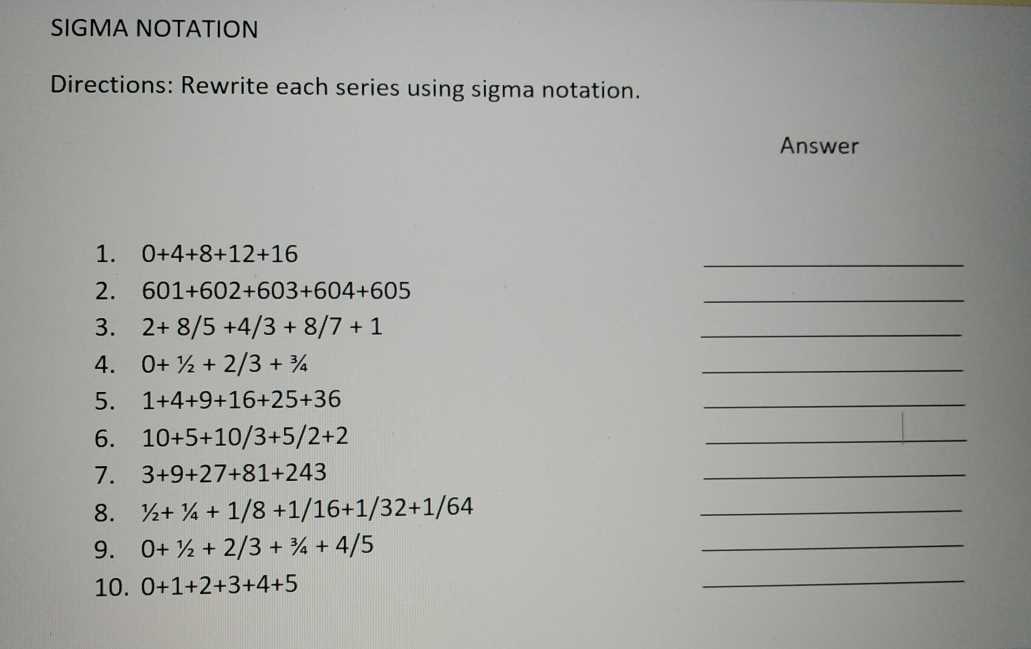
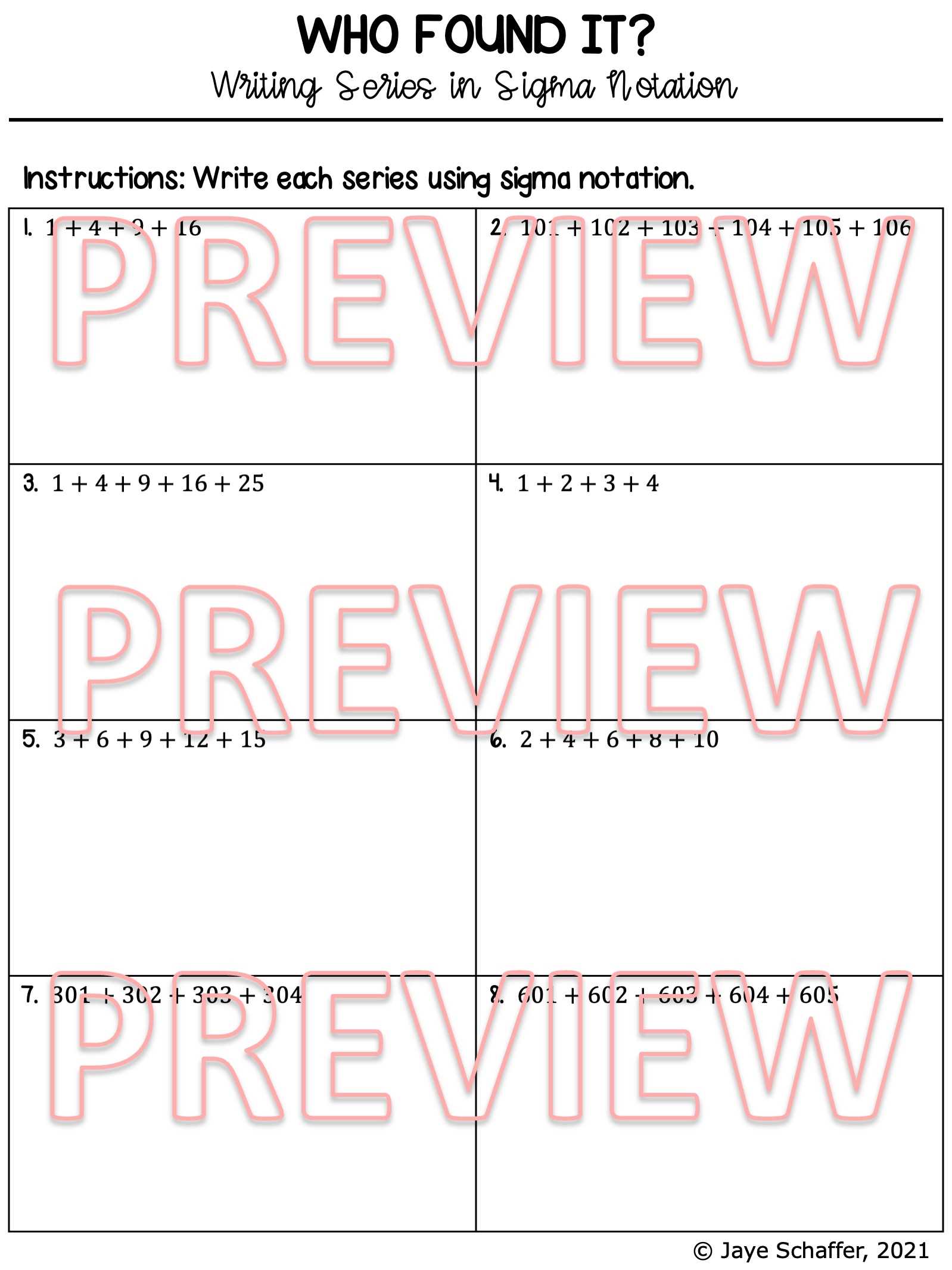
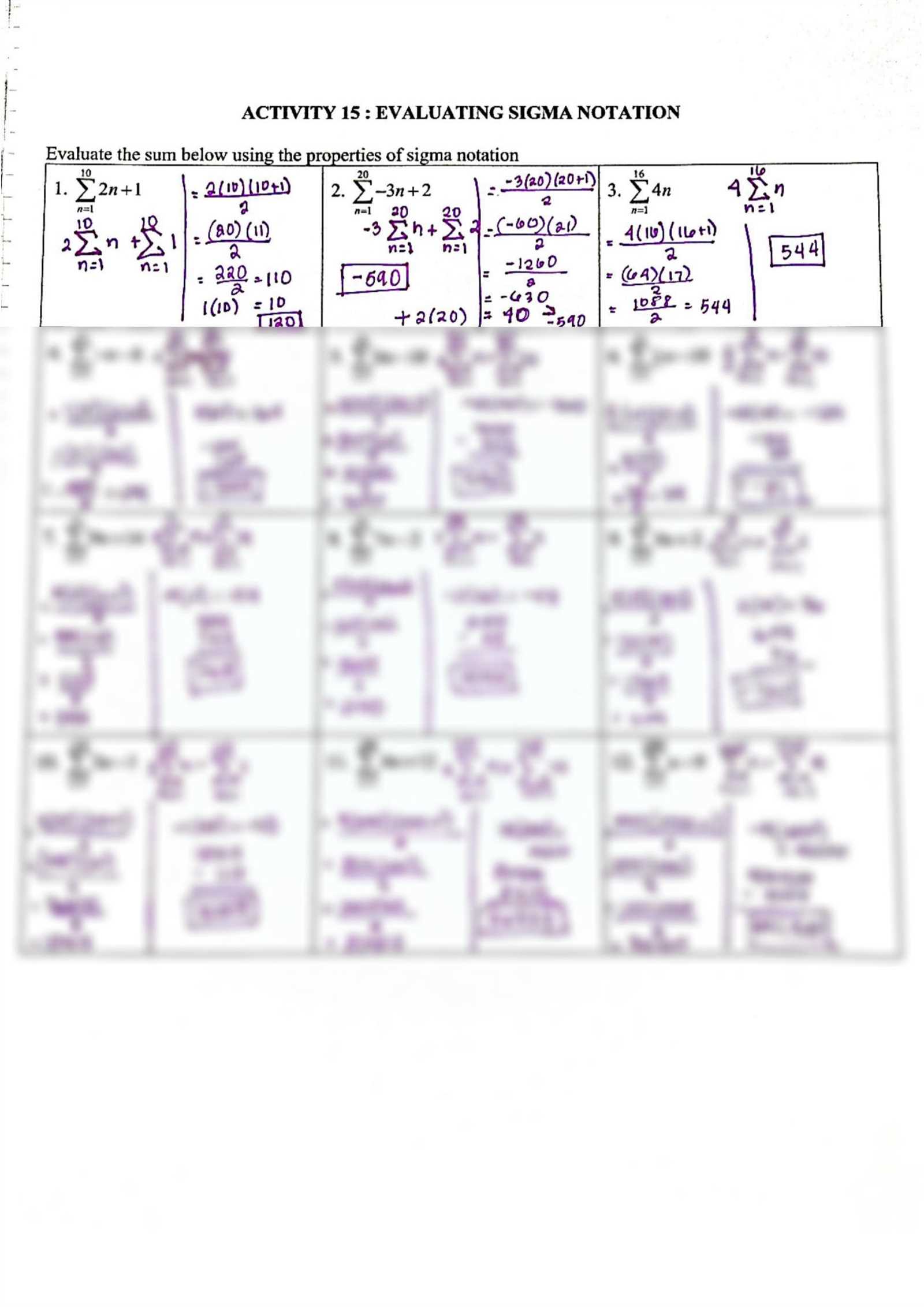
Sigma Notation Worksheet Answers and Solutions

In mathematics, understanding the process of adding sequences of numbers is a fundamental skill. This method helps in analyzing various patterns, calculating series, and solving complex problems. Mastering the steps involved can greatly enhance your ability to handle a wide range of mathematical challenges.
Through practice, you can develop a deeper understanding of how to handle summations effectively. By following a clear and structured approach, you will be able to tackle both simple and more advanced problems with ease. The key is recognizing patterns and applying appropriate formulas for each situation.
Whether you are solving arithmetic series or exploring more intricate sequences, having a clear grasp of these techniques is essential. This section provides a comprehensive guide to help you improve your skills and confidently solve summation problems across different areas of mathematics.
Mathematical Summation Solutions

When working with the summing of sequences, having a solid understanding of how to break down and calculate these expressions is essential. This section provides clear examples and methods for solving various types of summation problems, focusing on different techniques and strategies that can be used in both simple and complex scenarios.
Step-by-Step Problem Solving
Each problem requires a methodical approach to ensure accurate results. By following a structured process, you can systematically evaluate the terms of the series and apply the correct formulas. Whether dealing with arithmetic or geometric progressions, breaking down the problem into manageable steps is crucial for finding the correct sum.
Common Challenges and How to Overcome Them
Some common mistakes when calculating sums include misinterpreting the bounds of the summation or failing to apply the right formula for a specific type of series. By paying close attention to the details and practicing regularly, you can avoid these pitfalls and gain confidence in solving more challenging problems efficiently.
Understanding Summation Basics
The concept of summing a series of terms is a fundamental skill in mathematics. This process allows us to find the total of a sequence by adding individual elements together. Learning how to approach these sums efficiently is essential for solving a wide range of mathematical problems.
At the core of this technique is the ability to identify the start and end points of the sequence, as well as the pattern of the terms. Understanding how to work with these variables enables you to compute the sum quickly and accurately. By recognizing the structure of a series, you can apply the correct method to find the result.
How to Solve Summation Expressions
Solving summation problems requires a clear approach to handle the series of terms effectively. The first step is to identify the pattern or rule governing the sequence, which will guide the calculation of the sum. By recognizing this structure, you can apply the correct method to determine the total value.
Once the pattern is established, the next step is to break the expression into manageable parts. Start by evaluating the first few terms to understand the progression. Use the formula associated with the type of series to simplify the problem and compute the sum quickly. With consistent practice, these steps become intuitive, making the process smoother over time.
Step-by-Step Approach to Summations
When solving summation problems, following a systematic approach is crucial to ensure accurate results. Breaking the process into clear steps allows you to tackle each part of the series without feeling overwhelmed. By focusing on one term at a time, you can gradually build up to the final sum.
1. Identify the First and Last Terms
The first step is to pinpoint the starting and ending points of the series. This helps establish the boundaries and ensures that you are summing the correct terms. Once you have this information, you can proceed with calculating each element in between.
2. Apply the Formula or Rule
Next, use the appropriate formula or rule to compute the sum. Depending on the type of series, different strategies may be required. For example, an arithmetic series requires a specific sum formula, while a geometric series will follow its own rules.
| Term | Value |
|---|---|
| 1st Term | 3 |
| 2nd Term | 5 |
| 3rd Term | 7 |
| 4th Term | 9 |
| 5th Term | 11 |
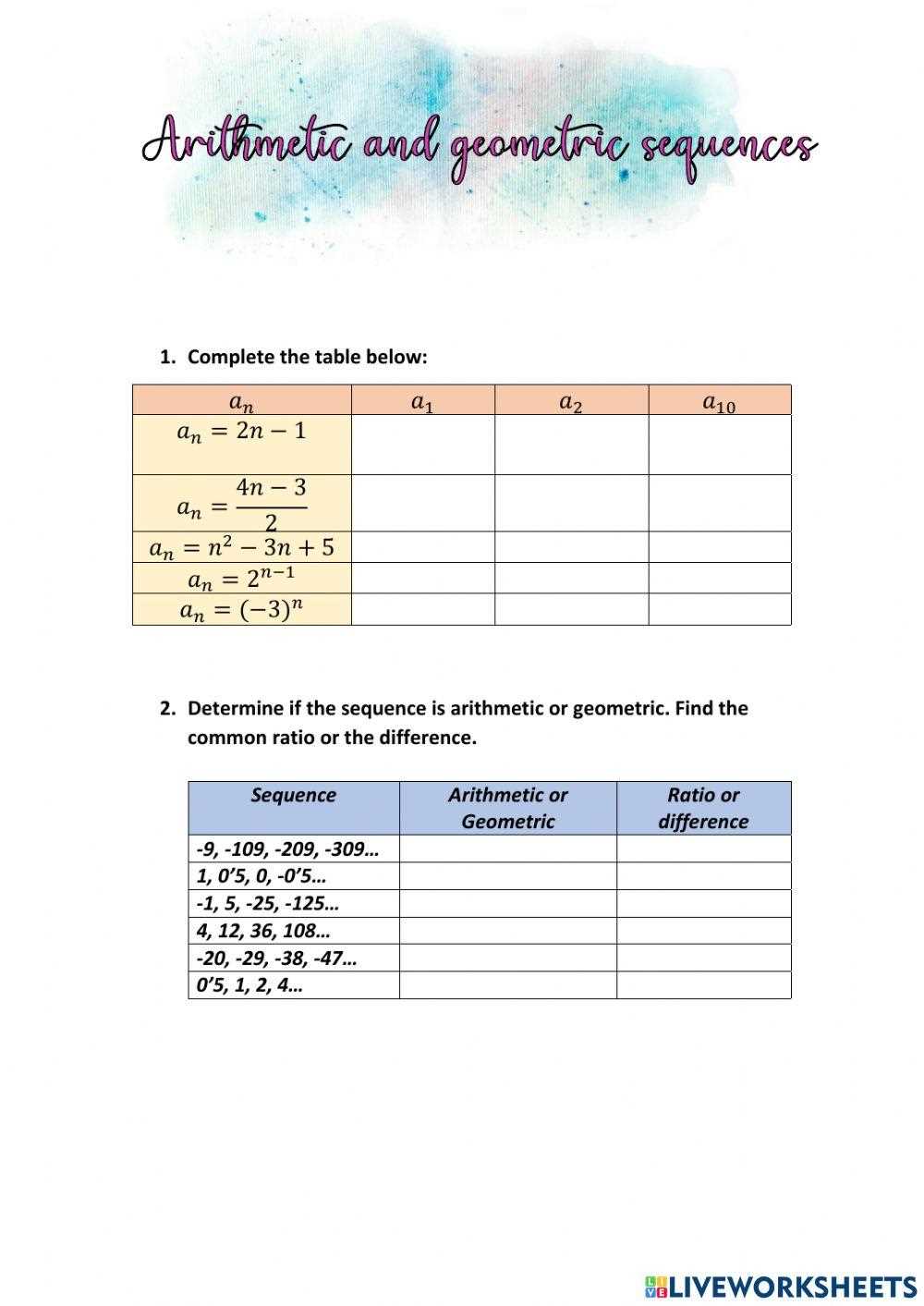
Key Concepts in Summation Techniques
Understanding the key concepts behind summing sequences is essential for solving problems efficiently. At the core, this involves recognizing how to identify the sequence structure, apply the correct formulas, and compute the total sum. These concepts are fundamental for both simple and advanced calculations.
1. Identifying the Sequence Type
To solve summation problems, it’s important to first identify the type of sequence you’re working with. Sequences can be arithmetic, geometric, or follow other patterns. Recognizing the type allows you to apply the right formula to calculate the sum.
2. Understanding the Bounds and Step Size
The bounds of a sequence refer to the starting and ending points of the sum. The step size determines the interval between terms. Knowing these helps in correctly interpreting the sequence and applying the right methods to solve the problem accurately.
Common Errors in Summation Calculations
When working with summation problems, several common mistakes can lead to incorrect results. These errors often occur due to misunderstandings of the sequence structure, misapplication of formulas, or overlooking important details such as bounds or step sizes. Being aware of these issues can help prevent mistakes and improve accuracy.
1. Incorrect Interpretation of Sequence Bounds
One of the most frequent errors is misunderstanding the starting and ending points of the sequence. Failing to correctly identify the first and last terms can result in an incomplete or incorrect sum. Always double-check the boundaries of the sequence before proceeding with the calculation.
2. Applying the Wrong Formula
Another common mistake is using the wrong formula for the sequence type. For example, arithmetic and geometric series require different methods. Ensure you are using the correct summation formula based on the pattern of the sequence you are working with.
Examples of Summation Solutions
To better understand how to solve summation problems, it’s helpful to look at specific examples. By working through various types of sequences, you can learn how to apply the right methods and formulas to find the total sum. These examples will demonstrate the steps needed to calculate the sum for both simple and more complex series.
Example 1: Arithmetic Sequence
Consider the following arithmetic series: 3 + 6 + 9 + 12. We can calculate the sum using the formula for an arithmetic sequence. In this case, the first term is 3, the common difference is 3, and there are 4 terms in total.
| Term | Value |
|---|---|
| 1st Term | 3 |
| 2nd Term | 6 |
| 3rd Term | 9 |
| 4th Term | 12 |
Example 2: Geometric Sequence
Now consider a geometric series: 2, 6, 18, 54. This series has a first term of 2 and a common ratio of 3. To find the sum, we apply the formula for a geometric sequence.
| Term | Value |
|---|---|
| 1st Term | 2 |
| 2nd Term | 6 |
| 3rd Term | 18 |
| 4th Term | 54 |
Tips for Mastering Summation Techniques
Mastering the art of summing series is a critical skill for solving many mathematical problems. Whether you’re dealing with basic or complex sequences, improving your understanding of the process can make a significant difference in your ability to calculate sums quickly and accurately. These tips will help you build a strong foundation and avoid common mistakes along the way.
1. Practice Regularly with Different Sequences

The more you practice, the more familiar the process will become. Work with various types of sequences–arithmetic, geometric, and others–to get a feel for the different patterns. This exposure will help you recognize the structures more easily and apply the appropriate formulas.
2. Break Down Problems into Manageable Steps
Instead of tackling the entire sum at once, break the problem into smaller parts. Start by identifying the first and last terms, then calculate the intermediate values step by step. This method will make the process more organized and reduce the chance of errors.
Applications of Summation Techniques in Math
Summing series plays a central role in many areas of mathematics. It is used to simplify complex problems, calculate totals over a range of values, and analyze patterns within data. Understanding how to apply these methods is essential for solving real-world mathematical challenges, from basic calculations to advanced theoretical analysis.
1. Calculating Areas and Volumes

One important application of summing series is in calculating areas under curves or volumes of solids. By approximating the area of irregular shapes using small sums of areas of rectangles or other geometric figures, we can derive formulas for more complex shapes. This method is particularly useful in integral calculus.
2. Analyzing Sequences in Number Theory
Summation techniques are also widely used in number theory to explore patterns and properties of numbers. For example, the sums of integers or prime numbers can be analyzed to uncover insights into their distribution. These summations form the foundation of many proofs and theorems in number theory.
Difference Between Summation and Product Methods
Both summation and product methods are used to calculate the total of a series, but they serve different purposes and operate in distinct ways. While one method is focused on adding the terms of a sequence, the other multiplies the terms. Understanding the difference between these two operations is crucial for applying them correctly in various mathematical contexts.
In the summation method, the focus is on adding terms together, often to find the total sum of a series or to approximate a larger quantity. On the other hand, the product method involves multiplying terms within a sequence, which is used for calculating the cumulative product or the total of multiplicative relationships.
Solving Complex Summations with Series
When dealing with more complicated summations, it is essential to break down the problem into smaller, manageable steps. By applying systematic techniques, even complex sums can be simplified and solved. In this section, we will explore strategies to handle challenging summation problems, step by step, using a methodical approach.
Breaking Down the Problem
The first step in solving complex summations is identifying the sequence and understanding its pattern. This can involve arithmetic or geometric series, or even more intricate functions. Once the structure is clear, the following approach can be applied:
- Identify the first and last terms of the sequence.
- Determine the rule or function governing the sequence.
- Check if a standard summation formula applies, such as for an arithmetic or geometric series.
- If necessary, break the summation into smaller parts to simplify calculations.
Using Decomposition for Tougher Problems
For more advanced problems, it may be helpful to decompose the summation into multiple simpler sums. This method can make otherwise complicated sums much easier to handle. For example, if a summation includes both linear and quadratic terms, separate the two and calculate each part individually.
- Decompose the sequence into simpler components.
- Apply the relevant formulas to each part.
- Combine the results to find the total sum.
Understanding Summation Bounds in Series
When working with summations, the bounds play a crucial role in determining which terms are included in the sum. These limits define the starting and ending points of the sequence, guiding the summing process. Grasping how to interpret and manipulate these bounds is key to solving summation problems accurately.
Lower and Upper Bounds
The lower bound indicates where the summation begins, while the upper bound marks where the summation ends. For example, in a summation sequence, the lower bound might specify the first term, and the upper bound could point to the final term to be added. These bounds help control the range of values to be considered within the series.
Adjusting Bounds for Complex Sequences
In more complicated problems, it is sometimes necessary to adjust the bounds to fit the problem’s structure. For instance, you might encounter cases where the summation needs to be split into separate intervals. By changing the bounds, you can isolate portions of the series and solve them individually, ensuring accuracy in the final result.
Exploring Infinite Series Summations
In mathematics, certain summations extend infinitely, meaning they continue without an end. These types of series require special attention because their behavior differs from finite sums. Understanding how to approach infinite series is essential for solving problems in calculus and analysis.
Convergence and Divergence
One of the key aspects of infinite series is determining whether they converge or diverge. A series converges if its terms approach a finite value as more terms are added. Conversely, it diverges if the terms do not approach a specific value. Identifying convergence or divergence helps in understanding whether the infinite sum has a meaningful result.
- Convergence: The series approaches a finite limit as more terms are added.
- Divergence: The series grows indefinitely and does not approach a finite value.
Techniques for Evaluating Infinite Series
There are several techniques to evaluate infinite series, including the use of specific formulas and convergence tests. Some of the most common methods involve:
- Geometric Series Test: Used when the series has a common ratio between successive terms.
- Integral Test: Involves integrating the function that represents the terms of the series.
- Ratio Test: Compares the ratio of successive terms to determine convergence or divergence.
By applying these methods, mathematicians can determine whether an infinite sum converges to a specific value or whether it will continue indefinitely.
Using Summation for Series
Summing sequences of terms efficiently is a key skill in mathematics. By representing series in a compact form, it becomes easier to understand their structure and solve problems related to them. This method is especially helpful when working with both finite and infinite sums. In this section, we will explore how to express and evaluate series using summation techniques.
Writing Series in Summation Form
When expressing a series in summation form, it is important to identify the pattern of the sequence and use an appropriate formula to represent it. A typical series is written as a sum of terms, where each term follows a consistent rule. The general structure of a summation includes:
- Starting Index: Indicates where the summation begins.
- End Index: Specifies where the summation ends.
- General Term: Describes the formula or function used to generate each term.
Applications of Summation for Series
Summation is useful in various areas of mathematics, such as in calculating the sum of arithmetic or geometric series, evaluating infinite sums, and solving problems in calculus. Some common uses include:
- Calculating Total Sums: Using summation to find the total of all terms in a series.
- Approximation of Functions: Expressing functions as series to approximate complex expressions.
- Solving Problems in Probability: Summing probabilities in random processes.
By mastering the use of summation, mathematicians and students can simplify the process of adding sequences and make solving problems more efficient.
Summation and Arithmetic Sequences
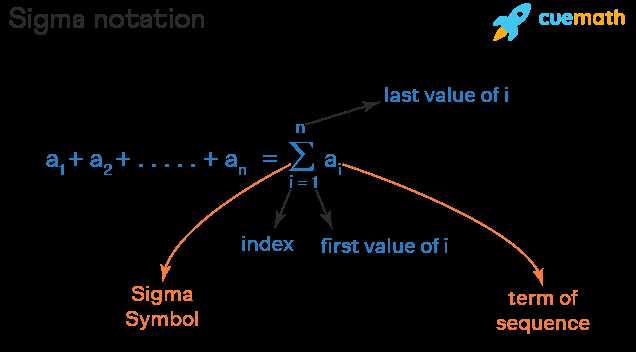
Arithmetic sequences are a fundamental concept in mathematics, where each term increases by a constant difference from the previous one. Summation provides a systematic method to calculate the total of all terms in such sequences. This process is essential for evaluating sums in both finite and infinite arithmetic series. Understanding how to express and calculate the sum of an arithmetic sequence can greatly simplify many mathematical problems.
Expressing Arithmetic Sequences Using Summation
In an arithmetic sequence, the difference between consecutive terms remains constant. When using summation to express an arithmetic sequence, the general formula involves identifying the first term, the common difference, and the number of terms. The formula for the sum of an arithmetic sequence can be written as:
- First Term: The initial term of the sequence.
- Common Difference: The constant difference between consecutive terms.
- Number of Terms: How many terms are included in the sum.
Applications of Arithmetic Sequence Summation

Summing arithmetic sequences has wide-ranging applications in mathematics, particularly in areas such as algebra and number theory. Some practical uses include:
- Calculating Total Costs: In financial models where costs increase by a fixed amount over time.
- Analyzing Growth Patterns: In populations or investments that grow at a steady rate.
- Solving Linear Equations: In problems involving evenly spaced intervals or progressions.
By understanding how to use summation for arithmetic sequences, students and professionals can quickly and accurately calculate the sums of these types of sequences.
Calculating Summations with Formulas
In many mathematical problems, it is necessary to quickly calculate the sum of a sequence of numbers. Instead of adding each term individually, there are efficient formulas that allow us to compute these sums directly. These formulas are particularly useful for arithmetic and geometric progressions, as they provide a quick way to obtain the total sum without manually adding each value in the sequence.
Arithmetic Sequence Sum Formula
The sum of an arithmetic sequence, where the difference between consecutive terms is constant, can be calculated using the following formula:
- Sum Formula: S = (n/2) × (2a + (n – 1) × d)
- Where:
- S is the sum of the sequence.
- n is the number of terms in the sequence.
- a is the first term in the sequence.
- d is the common difference between terms.
Using this formula, you can quickly determine the sum of any arithmetic sequence without the need to add each term individually.
Geometric Sequence Sum Formula
For geometric sequences, where each term is multiplied by a constant factor to obtain the next term, a different formula is used. The sum of the first n terms of a geometric sequence is given by:
- Sum Formula: S = a × (1 – r^n) / (1 – r) (for r ≠ 1)
- Where:
- S is the sum of the sequence.
- a is the first term in the sequence.
- r is the common ratio between terms.
- n is the number of terms in the sequence.
This formula provides a direct way to calculate the sum of a geometric sequence, which can be particularly helpful in problems involving exponential growth or decay.
By using these formulas, complex summation problems become much simpler to solve, allowing for faster and more accurate calculations in a wide range of mathematical and real-world applications.
Practical Examples of Summation Applications
Summation techniques are widely used in various fields of mathematics and science to simplify complex calculations. These methods are applied in problems involving series, patterns, and accumulation of quantities. Understanding how to apply summation in practical scenarios can help streamline processes and provide quick solutions to problems that would otherwise require time-consuming calculations.
Example 1: Calculating Total Revenue
In business, summation techniques can be used to calculate total revenue over a series of time periods. For example, a company might want to find the total revenue from sales over a number of months, where the sales in each month follow a specific pattern. The total revenue can be calculated by adding the revenue for each month in the series.
| Month | Revenue (in dollars) |
|---|---|
| January | 5000 |
| February | 5500 |
| March | 6000 |
| April | 6500 |
The total revenue over the four months can be found by summing the individual revenues:
Total Revenue = 5000 + 5500 + 6000 + 6500 = 23000 dollars
Example 2: Summing the Areas of Rectangles
In geometry, summation is frequently used to find the total area of irregular shapes composed of multiple smaller rectangles. For instance, if you have a series of rectangles with different lengths and widths, you can sum the areas of each rectangle to find the total area of the entire shape.
| Rectangle | Length (m) | Width (m) | Area (m²) |
|---|---|---|---|
| 1 | 4 | 2 | 8 |
| 2 | 6 | 3 | 18 |
| 3 | 5 | 4 | 20 |
The total area is calculated as:
Total Area = 8 + 18 + 20 = 46 m²
These examples demonstrate how summation methods can be applied to real-world problems, making it easier to compute totals, areas, and other quantities that are part of a sequence or series.