USA Test Prep Answer Key Algebra 1

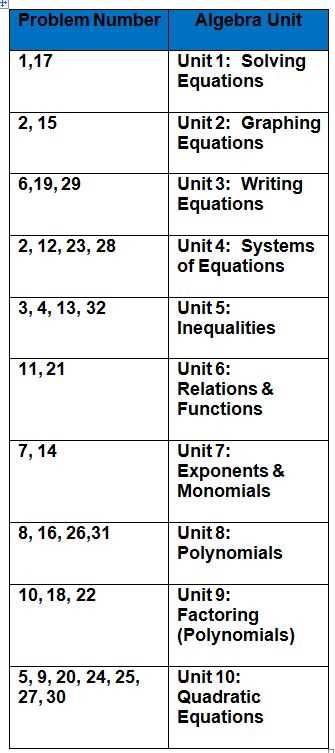
Preparing for mathematics assessments requires more than just memorizing formulas. It involves understanding the underlying principles that shape each problem. By gaining insight into how solutions are derived and identifying the most effective problem-solving strategies, students can significantly improve their performance.

Whether you’re facing practice questions or preparing for a real exam, having a structured approach to reviewing solutions can be incredibly beneficial. This approach not only helps clarify concepts but also provides confidence in applying mathematical techniques to solve a variety of problems. Through focused practice and analysis, students can overcome common hurdles and sharpen their skills.

Examining solutions closely enables learners to identify patterns and methods that are commonly used in various types of questions. Understanding these patterns can lead to more efficient solving strategies and better overall results. With the right guidance and practice, anyone can develop a strong foundation and succeed in their mathematical studies.

USA Test Prep Answer Key Algebra 1

Mastering the fundamentals of mathematical assessments involves more than just learning formulas and solving problems. A structured approach to understanding each step in the solution process can significantly enhance comprehension and performance. This section delves into how solutions can be effectively utilized to reinforce learning and provide clarity on commonly encountered questions.

Breaking Down Solutions for Better Understanding

Each problem in a mathematical evaluation is an opportunity to grasp the application of core concepts. By carefully examining the steps involved in each solution, students can gain a deeper understanding of how mathematical principles are applied in different contexts. Reviewing solutions allows individuals to recognize recurring patterns and methodologies that can streamline their problem-solving approach.

Maximizing Learning Through Review

Effective study strategies often include revisiting problems and solutions multiple times. This process helps reinforce concepts and enables learners to identify areas where they might need further practice. With continuous review, students can improve both their accuracy and efficiency, ultimately achieving better results in their assessments.

Understanding Algebra 1 Test Format

Successfully navigating a mathematical evaluation requires familiarity with its structure and the types of questions that may appear. Knowing what to expect allows students to approach the assessment with confidence and a clear strategy. This section provides insight into the general organization of such evaluations and key areas to focus on during preparation.

Key Elements of the Exam Structure

The structure of a typical math evaluation is designed to test a variety of skills, ranging from basic concepts to more complex problem-solving abilities. Understanding the layout can help students allocate time efficiently and avoid feeling overwhelmed during the exam. Key elements usually include:

• Multiple-choice questions assessing basic understanding
• Short-answer problems that require step-by-step solutions
• Word problems designed to test real-world application of concepts
• Longer, multi-step problems that challenge analytical skills

Strategies for Navigating the Format

Adapting to the format of the evaluation is essential for success. Here are some tips to help manage the exam effectively:

1. Familiarize yourself with question types – Understanding the format of each question type can make it easier to identify the best approach during the exam.
2. Practice time management – Divide your time wisely between different sections of the exam to avoid spending too long on one question.
3. Check your work – If time permits, review your answers to catch any errors or oversights.

By keeping these strategies in mind, students can approach the evaluation with a systematic plan, making it easier to tackle each question with clarity and confidence.

Key Concepts in Algebra 1

To excel in any mathematical evaluation, understanding the fundamental principles is crucial. A strong grasp of the core concepts not only helps in solving problems accurately but also enhances the ability to approach complex questions with confidence. This section highlights the most important ideas that form the foundation of mathematical studies at this level.

Equations and Variables are at the heart of most problems. Understanding how to manipulate unknowns and solve for their values is essential. Whether it’s a simple linear equation or a more complex expression, recognizing the relationship between variables is a skill that can be applied across various problem types.

Functions are another critical area. These describe how one quantity depends on another and are foundational for understanding graphing and other advanced topics. Being able to identify different types of functions and interpret them effectively is key to success in more advanced mathematics.

Factoring is a vital tool in simplifying expressions and solving equations. The process of breaking down expressions into their factors can make seemingly difficult problems more manageable. Mastery of factoring techniques is important for solving quadratic equations and many other problems.

Linear Relationships are also fundamental. Understanding how to represent and solve problems involving lines, slopes, and intercepts is essential for both algebraic problem-solving and real-world applications. These concepts are used in everything from graphing to solving systems of equations.

By focusing on these key concepts, students can build a solid mathematical foundation that will support their ability to tackle increasingly complex challenges with greater ease.

Common Challenges in Algebra 1

Mathematical subjects can present a variety of obstacles, and many students face similar difficulties when learning core concepts. These challenges can hinder progress and cause frustration if not addressed early on. Understanding the common issues that arise can help students approach their studies with the right mindset and strategies for overcoming them.

One frequent challenge is manipulating equations. Many learners struggle with understanding how to isolate variables or apply operations correctly. This can be especially difficult when working with more complex expressions or when dealing with fractions and negative numbers. Mastering these skills is essential for progressing to more advanced topics.

Word problems also present a significant hurdle. Translating real-life scenarios into mathematical expressions can be confusing, particularly when students are unfamiliar with the language used. Breaking down the information step-by-step and identifying key numbers and relationships can help clarify these types of problems.

Another common difficulty is graphing. While the concept may seem straightforward, plotting accurate points and interpreting the relationships between them can be tricky. A strong understanding of slope, intercepts, and how to read graphs is necessary to avoid errors in this area.

Factoring is another area where many students face difficulty. The process of breaking down expressions into smaller components can seem abstract and intimidating, especially when dealing with quadratic equations or higher-degree polynomials. Practicing different factoring techniques can help alleviate this challenge and make the process feel more intuitive.

Recognizing these challenges early and practicing key skills can help students navigate through them more effectively, ultimately leading to greater success and confidence in their studies.

How to Use the Answer Key

Accessing solutions to problems can be a valuable resource in the learning process, but it’s important to use this tool effectively. Simply looking at the answers without understanding the steps can hinder long-term mastery of the subject. Instead, a strategic approach to reviewing solutions can enhance comprehension and improve problem-solving abilities.

Reviewing Each Step Carefully

When using a solution guide, it’s essential to focus not just on the final result but also on the process that led to it. By breaking down each step, you can identify patterns, strategies, and techniques that can be applied to similar problems. This method helps reinforce the concepts and ensures that you understand how to reach the correct answer on your own.

Identifying Common Mistakes

Using a solution guide is also a great way to spot mistakes in your own work. By comparing your approach to the correct steps, you can identify where errors occurred and how to avoid them in the future. This self-analysis improves your ability to spot mistakes before they become habits.

Step	Your Solution	Correct Solution
Step 1: Simplify the equation	2x + 4 = 10	2x + 4 = 10
Step 2: Subtract 4 from both sides	2x = 6	2x = 6
Step 3: Divide by 2	x = 3	x = 3

In the example above, comparing each step helps reinforce the correct process for solving linear equations. By focusing on each stage, students can see how small changes affect the final result and gain confidence in their ability to apply the same steps independently.

Essential Algebra 1 Topics Covered

Understanding the foundational concepts in mathematics is critical for success in any advanced studies. This section highlights the core topics that form the backbone of mathematical problem-solving at the introductory level. Mastering these areas will not only prepare you for future courses but also enhance your ability to apply mathematical reasoning in real-world situations.

Equations and Expressions

One of the first and most important topics involves working with equations and expressions. These are the building blocks of solving mathematical problems, and students must be able to manipulate both sides of an equation or expression to isolate variables and find solutions. Whether solving simple linear equations or more complex systems, this skill is crucial for progressing in the subject.

Linear Relationships and Graphing

Another essential topic is understanding linear relationships and their graphical representations. Students learn to plot points on a coordinate plane and interpret how these points form lines. Understanding the concepts of slope and intercepts is vital for solving problems involving rates of change and real-world applications.

Mastering these topics forms a solid mathematical foundation, equipping students with the tools to tackle a wide range of problems with confidence and clarity. Whether you are solving equations or graphing lines, each of these concepts plays a pivotal role in ensuring academic success.

Tips for Effective Test Preparation

Proper preparation is the key to performing well in any academic evaluation. A strategic approach to studying not only helps you grasp essential concepts but also builds confidence and reduces anxiety on the day of the assessment. Here are some practical tips to ensure you’re fully prepared for success.

Create a Study Plan

Effective preparation starts with a well-organized study schedule. Instead of cramming all at once, break down your study time into manageable sessions and focus on specific topics each time. This method promotes better retention and reduces stress.

• Set specific goals for each study session (e.g., mastering one concept or solving a set of problems).
• Prioritize challenging areas where you need the most improvement.
• Review regularly to reinforce your understanding.

Practice Consistently

Consistent practice is essential to mastering mathematical concepts. The more you practice, the more familiar you become with problem-solving techniques, which helps build confidence for tackling new problems during the actual evaluation.

1. Work through sample problems from various sources, including practice exercises and previous assessments.
2. Time yourself during practice sessions to improve speed and accuracy.
3. Review mistakes to understand where errors occurred and how to avoid them in the future.

Stay Organized and Rested

Keep your study materials organized and take regular breaks to prevent burnout. Adequate rest is just as important as study time, as it allows your brain to process and retain information more effectively.

• Keep notes and materials organized so you can easily access them when needed.
• Ensure a good night’s sleep before the evaluation to ensure optimal focus and performance.

By incorporating these strategies into your routine, you will be better equipped to approach the evaluation with confidence and clarity, ultimately enhancing your chances of success.

Common Mistakes to Avoid in Algebra

When working through mathematical problems, it’s easy to make mistakes, especially when dealing with complex equations and expressions. Identifying and understanding these common errors can help you avoid them and improve your overall problem-solving abilities. By being mindful of the most frequent pitfalls, you can streamline your approach and build a stronger foundation for tackling future problems.

Incorrectly Simplifying Equations

One of the most common errors is simplifying equations incorrectly. This often happens when students forget to apply the correct order of operations or mismanage terms during simplification. Paying close attention to the rules for combining like terms and applying operations to both sides of an equation is crucial for avoiding these mistakes.

Misinterpreting Word Problems

Word problems often confuse students because they require translating real-world situations into mathematical expressions. A frequent mistake is misinterpreting the key information or overlooking important details. Carefully reading the problem and breaking it down step by step will help you avoid making these errors.

Problem	Common Mistake	Correct Approach
Solve 2x + 3 = 11	Incorrectly subtracting 3 from both sides	Correctly subtract 3 from both sides: 2x = 8, then divide by 2
Word problem: “The sum of a number and 7 is 15.”	Misinterpreting “sum” as subtraction	Translate correctly: x + 7 = 15

Understanding these common errors and applying strategies to avoid them can drastically improve your accuracy and efficiency when solving problems. By recognizing your mistakes and learning from them, you’ll become more confident in your abilities and better prepared for future challenges.

Time Management During Algebra Tests

Effective time management is a crucial skill when it comes to performing well in any formal assessment. Without a structured approach, students may find themselves rushing through questions or spending too much time on a single problem. By planning ahead and managing the available time wisely, you can improve both your performance and your confidence during the evaluation.

Prioritize Easy Questions

Start by tackling the easier problems first. These questions are usually straightforward and require less time to complete. By answering them quickly, you can gain momentum and build confidence for the more challenging problems later on. This approach also ensures that you don’t run out of time for questions you can easily solve.

• Quickly scan through the entire paper to identify questions you can solve with minimal effort.
• Answer the easy ones first to ensure they are completed before moving on to more complex problems.

Manage Time for Difficult Problems

For more complex questions, it’s important to allocate enough time to solve them properly. If you get stuck, don’t waste valuable minutes trying to figure out a single problem. Instead, move on and return to it if time permits.

• Set time limits for each question based on its difficulty. For example, allocate more time for multi-step problems.
• Leave difficult problems for later and come back to them after finishing the easier ones.

By following these strategies, you can make the most of the time available and ensure that you complete as much of the assessment as possible with accuracy and confidence. With practice, you will refine your ability to manage time effectively during evaluations.

How to Interpret Solution Steps

Understanding the process behind solving a mathematical problem is just as important as finding the final answer. By interpreting the steps involved, you gain a deeper comprehension of the methods used, which allows you to apply similar strategies to other problems. Knowing how each operation affects the equation and why it’s done can help you develop critical problem-solving skills.

Break Down Each Step

When reviewing a solution, it’s essential to break the steps down logically. This allows you to see how each operation contributes to simplifying or solving the problem. Instead of simply memorizing procedures, focus on understanding why each step is necessary.

• Identify operations such as addition, subtraction, multiplication, and division.
• Understand why each step was taken (e.g., isolating a variable or combining like terms).
• Link each step to the overall goal of solving the problem.

Practice with Similar Problems

After reviewing a solution, apply the same method to similar problems. This will reinforce your understanding and allow you to spot any potential mistakes in your reasoning. The more you practice interpreting solution steps, the more intuitive it becomes to recognize patterns and apply appropriate techniques.

1. Work through similar exercises to test your understanding of each step.
2. Compare your solution with provided examples to check for errors or alternate approaches.
3. Ask questions if any part of the solution is unclear, and seek clarification from reliable resources.

By focusing on the logic and reasoning behind each step, you can develop a better grasp of the mathematical principles involved and enhance your ability to tackle more complex problems with confidence.

Practical Practice Exercises for Mastery

To truly master mathematical concepts, consistent practice is essential. While reading through solutions and theories can provide a foundation, applying those concepts through exercises is what solidifies understanding. Practical practice allows you to become familiar with different problem types and strengthens your ability to solve them efficiently.

Engaging in regular exercises helps you build confidence and identify areas where further focus is needed. The more you practice, the better equipped you are to recognize patterns, apply techniques accurately, and approach new challenges with ease.

• Start with simple problems to build a strong foundation before progressing to more complex scenarios.
• Challenge yourself with progressively harder exercises that require multi-step solutions.
• Review your solutions and identify any mistakes to understand where your reasoning went wrong.

By incorporating practical exercises into your study routine, you can transform abstract concepts into practical skills. These exercises should cover a variety of problem types to ensure a comprehensive understanding, allowing you to apply what you’ve learned in real-world situations with confidence.

Improving Problem-Solving Skills

Enhancing your ability to solve problems efficiently requires developing a systematic approach and practicing critical thinking. The process of solving mathematical challenges goes beyond memorizing formulas; it involves analyzing the problem, selecting the best strategy, and applying your knowledge effectively. With consistent practice and the right techniques, you can sharpen your problem-solving skills and improve your overall performance.

Developing a Step-by-Step Approach

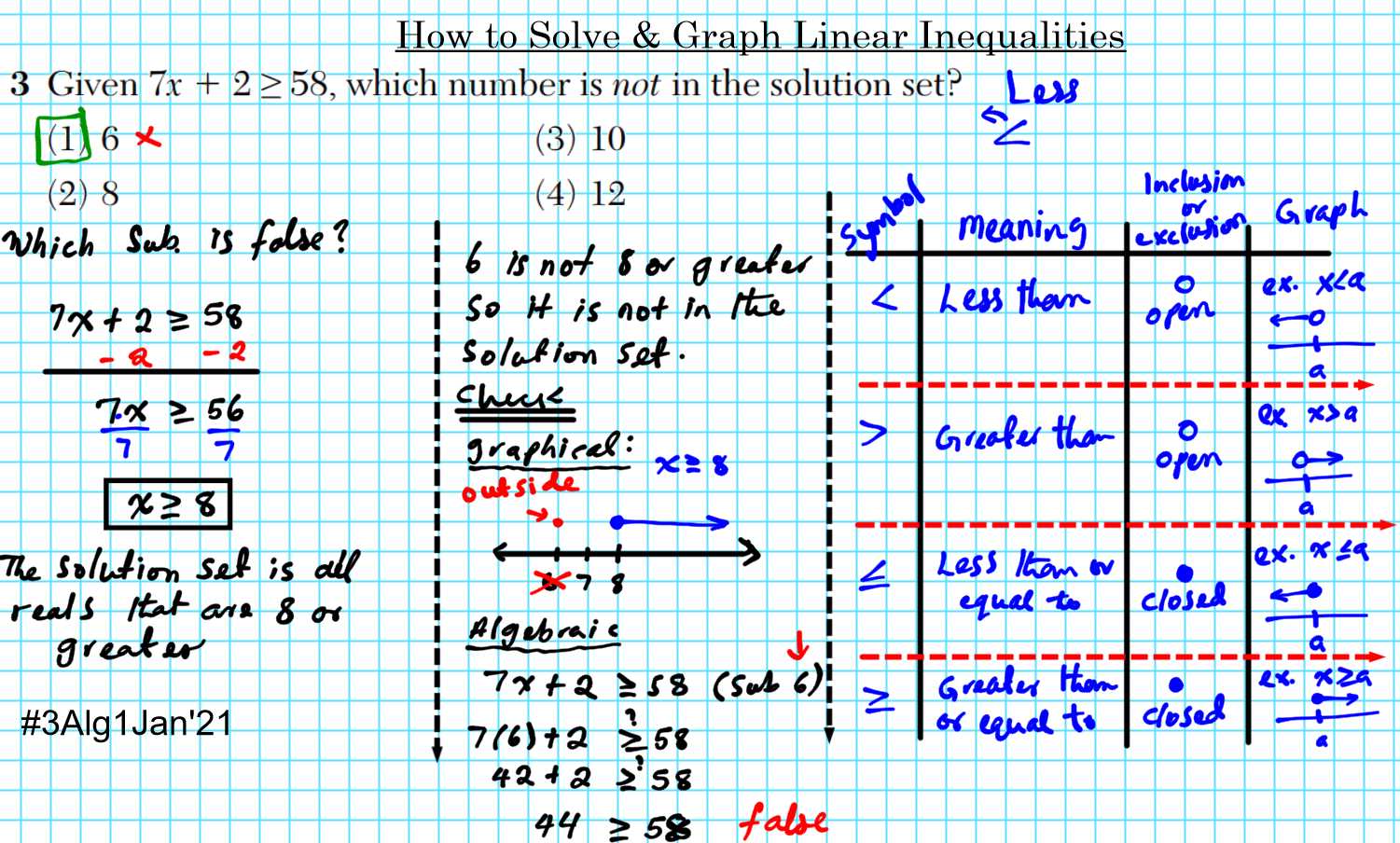
A clear, step-by-step method is essential for tackling complex problems. Breaking down the problem into manageable parts helps prevent confusion and ensures you don’t overlook crucial details. Start by understanding the problem, identifying knowns and unknowns, and planning your approach before executing any calculations.

• Understand the problem before attempting to solve it. Ensure you know exactly what is being asked.
• Identify relevant information and choose the best method for solving the problem.
• Execute in stages to prevent errors, checking each step for accuracy before moving forward.

Practicing Consistently

The key to improving problem-solving is consistent practice. Regularly engaging with problems of varying difficulty levels will help you become more comfortable with different techniques and recognize patterns more quickly. Over time, you will develop the ability to solve problems more efficiently, even under pressure.

• Set aside time each day or week for focused problem-solving practice.
• Work on a range of problems to familiarize yourself with diverse approaches and strategies.
• Analyze your mistakes to understand where you went wrong and improve your future solutions.

By honing your problem-solving abilities, you will be better equipped to handle increasingly difficult challenges with confidence, making your study sessions more productive and effective.

Using Online Resources for Extra Help

In today’s digital age, online platforms offer a wealth of resources that can provide additional support for mastering mathematical concepts. These resources are particularly valuable for those who need extra practice, clearer explanations, or a different perspective on challenging topics. By leveraging these tools, you can enhance your understanding and improve your problem-solving skills.

Online resources come in many forms, including interactive tutorials, video lessons, practice problems, and forums where you can ask questions and receive expert advice. These tools allow you to learn at your own pace, revisit difficult concepts, and access explanations in a variety of formats to suit your learning style.

Types of Helpful Online Tools

• Interactive Practice Platforms: Websites that offer guided practice problems help reinforce key concepts and allow you to track your progress.
• Video Tutorials: Many educational websites and YouTube channels feature experts explaining step-by-step solutions to problems.
• Forums and Communities: Online discussion boards provide an opportunity to ask questions, collaborate with peers, and find answers from experienced tutors.

Maximizing the Benefits of Online Learning

To get the most out of online resources, it’s important to use them strategically. First, identify which areas you need the most help with and focus your efforts on those topics. Set clear goals and stay consistent in using online tools to practice and reinforce what you’ve learned.

• Focus on weak areas: Use online resources to dive deeper into topics you find difficult, ensuring that you have a solid understanding before moving forward.
• Take advantage of free resources: Many websites offer free tutorials, worksheets, and exercises that can be accessed without any cost.
• Engage in community discussions: Participating in online forums or study groups can provide additional insights and alternative solutions to problems.

By incorporating online resources into your study routine, you can access a wide range of tools that cater to your individual learning needs, ultimately helping you achieve mastery and confidence in your studies.

Grading and Scoring Insights

Understanding how your work is assessed and scored is crucial for effective learning. Grading systems vary by institution, but the principles behind evaluating mathematical proficiency remain largely the same. Typically, assessment focuses on accuracy, problem-solving methods, and the clarity of explanations. Gaining insight into how you are graded can help you target areas that need improvement and refine your skills to achieve better results.

Evaluators generally look for a combination of correct answers and the logical steps that lead to those solutions. This approach ensures that students not only arrive at the correct final answer but also understand the process involved. Mastering the methods and presenting your work clearly are as important as achieving accuracy in the final result.

Key Factors in Grading

• Accuracy: The final solution must be correct and match the required format or answer.
• Process: Demonstrating the correct steps leading to the solution shows that you understand the underlying concepts.
• Clarity: Clear, well-organized work is easier to follow, and it shows that you can communicate your thought process effectively.

Strategies for Better Scoring

• Show Your Work: Always include intermediate steps when solving problems. This not only helps you catch mistakes but also demonstrates your problem-solving process.
• Understand the Rubric: Familiarize yourself with how your work will be graded. Knowing what the evaluator is looking for can guide how you present your solutions.
• Practice Regularly: Consistent practice with a variety of problems can help improve both accuracy and problem-solving techniques, leading to better results.

By understanding grading criteria and actively working to meet them, you can improve your performance and become more confident in solving complex problems. Focus on both accuracy and process, and your grades will reflect the effort and understanding you’ve developed.

Understanding Question Types

When preparing for assessments in mathematics, it’s important to familiarize yourself with the different types of questions you may encounter. Each question type evaluates a specific set of skills and understanding, so recognizing them can help you tailor your preparation and approach effectively. By breaking down the various formats, you can be better equipped to tackle any challenge presented during an exam.

Generally, questions fall into categories such as problem-solving, conceptual understanding, and application of formulas. Some may require calculations, while others test your ability to analyze and interpret information. Identifying the type of question allows you to strategize and determine the most efficient way to respond.

Common Question Formats

• Multiple Choice: You are given several possible answers, and you must choose the one that best fits the problem.
• Short Answer: Requires you to provide a specific numerical or written response, typically after performing calculations or applying rules.
• Word Problems: These questions present a real-world scenario and ask you to apply mathematical concepts to find a solution.
• True/False: You must determine whether a given statement is correct based on the concepts you’ve learned.
• Fill-in-the-Blank: You need to complete an equation or expression with the appropriate value.

Approaching Each Type

• For Multiple Choice: Eliminate clearly incorrect options first to improve your chances of selecting the correct answer.
• For Short Answer: Show all your work. Even if the final answer is incorrect, partial credit may be awarded for correct methods.
• For Word Problems: Identify the key information, break the problem down into manageable parts, and apply the right formula or method.
• For True/False: Review the wording carefully, and consider whether the statement holds true under all circumstances.
• For Fill-in-the-Blank: Make sure you understand the context and the relationship between different elements in the problem.

By understanding the various question types and practicing your response strategies, you can enhance your problem-solving skills and improve your overall performance. Take the time to review each format, and with regular practice, you’ll become more efficient at answering them correctly and confidently.

Test-Taking Strategies for Success

Successfully navigating an assessment requires more than just knowledge of the material–it involves effective strategies to maximize your performance under timed conditions. Understanding how to approach each section, manage your time, and stay focused can make a significant difference in your results. Implementing well-thought-out techniques allows you to work efficiently and confidently, even when faced with challenging problems.

By preparing not only the content but also the process of taking an exam, you can reduce stress and improve accuracy. From carefully reading each question to reviewing your answers at the end, each step contributes to an optimal performance. Developing strong test-taking habits ensures that you approach the exam with the best chance for success.

Effective Techniques

• Read Questions Thoroughly: Take time to read each question carefully before attempting to solve it. Look for key words and clues that will guide you toward the correct approach.
• Start with Easy Questions: Begin with the questions that you find most straightforward. This helps build confidence and ensures you earn easy points before tackling harder problems.
• Time Management: Allocate your time wisely. Spend an appropriate amount of time on each section, and don’t get stuck on difficult questions. Move on and return to them later if needed.
• Check Your Work: After finishing the exam, take a few minutes to go back and review your answers. Look for any mistakes or missed steps, especially in complex calculations.

Handling Difficult Questions

• Break It Down: For challenging problems, break them into smaller, more manageable parts. This can make them less intimidating and help you identify the correct method to apply.
• Eliminate Incorrect Options: When faced with multiple-choice or similar questions, eliminate the clearly incorrect answers first. This increases your chances of choosing the correct one, even if you’re unsure.
• Stay Calm: Maintain composure if you encounter a particularly tricky question. Staying calm will help you think more clearly and may allow you to spot the solution with a fresh perspective.

Incorporating these strategies into your approach will not only improve your performance but also enhance your ability to manage stress during exams. By practicing these techniques regularly, you’ll develop a more confident and efficient approach to any future assessments.

Reviewing Mistakes for Better Results

One of the most effective ways to improve your performance in any subject is by carefully reviewing your errors. Mistakes are not just setbacks–they offer valuable insights into areas that need further attention. By analyzing where and why you went wrong, you can uncover patterns, misconceptions, or gaps in knowledge that may be holding you back. This process of reflection can significantly enhance your understanding and boost your confidence for future assessments.

Rather than simply moving on after an incorrect answer, take the time to break down each mistake. Understand the reason behind the error and apply corrective measures to prevent it from happening again. This approach not only helps you learn from your mistakes but also strengthens your problem-solving skills, leading to improved results over time.

How to Review Mistakes Effectively

• Identify the Mistake: Start by pinpointing the exact error. Did you misinterpret the question? Was there a calculation mistake? Recognizing the type of mistake is the first step toward correcting it.
• Understand Why It Happened: Take a moment to reflect on why the mistake occurred. Was it due to a misunderstanding of the concept or a simple oversight? Identifying the root cause is crucial for improvement.
• Review the Correct Process: Go back to the steps involved in solving the problem. Look at the correct method and compare it with what you did. This will help you see where you deviated and how to approach similar problems more effectively in the future.
• Practice Similar Problems: After reviewing your mistakes, reinforce your understanding by practicing similar questions. This will help solidify the correct techniques and prevent similar errors in the future.

Tracking Progress

It’s helpful to track your mistakes over time. Keeping a record of the types of errors you make allows you to monitor your improvement and focus on areas that still need attention. Below is an example of how you might track your mistakes:

Problem Number	Type of Mistake	Correct Approach	Revisited Concept
1	Misinterpretation of question	Read the question carefully and identify keywords	Word problems
2	Calculation error	Double-check steps before finalizing answer	Operations with fractions
3	Incorrect formula used	Review relevant formulas for the problem type	Quadratic equations

By maintaining a record of mistakes and continuously revisiting key concepts, you’ll gradually develop a deeper understanding and improve your problem-solving abilities. This consistent practice is key to achieving better results in future assessments.

Preparing for Practice Assessments

Proper preparation is essential when approaching practice assessments. These exercises are designed to simulate actual evaluation conditions and help you gauge your level of understanding. By preparing effectively, you can identify areas of strength and areas that need further attention. It is crucial to approach these exercises with a clear strategy to maximize your results and build confidence for the actual evaluation.

Start by reviewing the material thoroughly before attempting any practice exercises. Break down the content into manageable sections, focusing on one concept at a time. This will ensure you don’t feel overwhelmed and allow for more focused practice. It’s also helpful to set aside regular study sessions leading up to your practice exercises to reinforce your understanding consistently.

Key Strategies for Effective Preparation

• Understand the Format: Familiarize yourself with the structure of the practice exercises. Knowing what to expect in terms of question types and topics will help you focus your studies on the most relevant areas.
• Review Previous Mistakes: Analyze past practice exercises to see where mistakes occurred. Understanding these errors helps you avoid repeating them and strengthens your grasp of the material.
• Set Realistic Goals: Define specific goals for each practice session. For instance, aim to improve your speed in solving specific types of problems or mastering a particular concept.
• Simulate Real Conditions: When practicing, try to replicate the conditions of the actual evaluation. Set a timer, limit distractions, and attempt to complete the exercises in one sitting to build endurance and time management skills.

Tracking Progress

Keep track of your progress over time to ensure that you’re improving. Monitoring your performance on practice exercises allows you to identify recurring challenges and areas that still require more attention. Below is an example of how you might track your progress:

Practice Session	Focus Area	Time Spent	Score Achieved	Areas to Improve
Session 1	Equations	45 minutes	80%	Solving word problems
Session 2	Functions	40 minutes	90%	Graphing functions
Session 3	Quadratics	50 minutes	70%	Factoring quadratics

By keeping a record of each practice session, you’ll be able to see how your preparation is progressing. Adjust your study strategy based on the results to ensure continuous improvement and optimal performance when it counts.