Core Connections Algebra Textbook Answers and Solutions

When studying complex mathematical topics, having access to clear, structured solutions is essential for mastering the material. This section aims to guide learners through the process of solving equations and problems, providing step-by-step guidance to ensure a deep understanding. Whether you’re tackling basic equations or more intricate scenarios, the ability to follow along with detailed explanations can make all the difference in building confidence and competence.

In the following content, you will find thorough explanations designed to clarify difficult concepts. By breaking down each problem into manageable steps, this approach allows you to grasp the underlying principles and apply them with ease. Learning by example plays a crucial role in reinforcing these mathematical strategies, ensuring that you not only solve problems but also understand the methods behind them.

Equipped with these detailed solutions, learners can confidently approach various challenges and enhance their skills with every problem they solve. The key is consistency and practice, which will allow you to gain proficiency and achieve greater success in your studies.

Core Connections Algebra Textbook Overview

This section provides a comprehensive look at the structure and content of the mathematical resource designed to help students understand key concepts and solve complex problems. It presents an organized approach to learning, ensuring that essential skills are built progressively. By focusing on different types of mathematical challenges, this guide prepares learners to tackle a variety of topics with clarity and precision.

Organized Learning Approach

The material is carefully structured to support students at every stage of their journey. It starts with foundational concepts and gradually introduces more advanced topics. This progression ensures that learners can develop a solid understanding, with each lesson building on the previous one. The goal is to foster critical thinking and problem-solving abilities that can be applied across various mathematical disciplines.

Key Concepts and Problem Solving

The main focus of this guide is to help students become proficient in solving mathematical problems by providing step-by-step examples. Each section highlights important principles, demonstrating their application through practical examples. This method not only teaches how to arrive at the correct solution but also emphasizes understanding the reasoning behind each step.

Why Algebra Answers Matter for Learning

Understanding the solutions to mathematical problems is essential for building a strong foundation in any field of study. Without clarity on how to reach the correct result, students may struggle to grasp fundamental concepts. The value of having access to detailed solutions goes beyond simply providing the right answers; it is about fostering a deeper understanding of the reasoning and methods behind each step. This approach equips learners with the tools to solve future problems independently and with confidence.

Here are some key reasons why having solutions available is crucial for effective learning:

• Clarifies Problem-Solving Steps: Seeing each step of a problem-solving process helps students understand how to break down complex tasks into manageable parts.
• Reinforces Key Concepts: Revisiting solutions allows learners to identify recurring patterns and techniques that apply across different problems.
• Builds Confidence: When students can confirm their work with a correct solution, it boosts their confidence and motivation to continue learning.
• Highlights Common Mistakes: Solutions often point out areas where learners tend to make mistakes, allowing them to avoid similar errors in the future.
• Improves Critical Thinking: Understanding how each step contributes to the overall solution encourages students to think critically about the methods they use.

In essence, having access to the correct solutions transforms the learning experience, offering students not only the answers but also the insight necessary to deepen their understanding and improve their skills over time.

Step-by-Step Solutions for Algebra Problems

Breaking down problems into manageable steps is one of the most effective ways to approach mathematical challenges. This method allows students to follow a logical sequence, ensuring they fully understand each part of the process. By walking through each solution step-by-step, learners can not only arrive at the correct result but also gain insight into the reasoning behind each action taken.

Understanding the Process

The key to mastering any mathematical problem lies in understanding the approach rather than just memorizing formulas. Each solution should be viewed as a series of logical decisions, with each step building on the previous one. By practicing this method, students can develop a deeper understanding of how different concepts are connected and how they apply to real-world scenarios.

Practicing with Examples

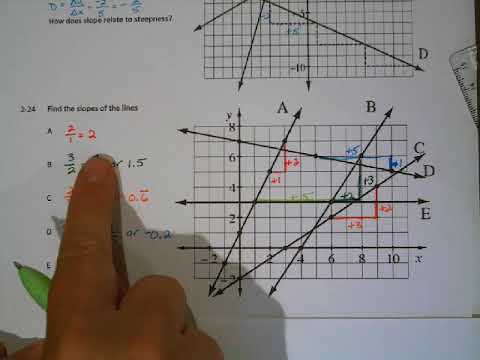
Working through multiple examples allows learners to solidify their understanding of the methods used to solve problems. Step-by-step solutions show not only the final answer but also how to arrive at it, which is crucial for reinforcing problem-solving skills. By tackling a variety of problems, students will build their confidence and ability to handle more complex challenges independently.

Common Mistakes in Algebra and How to Avoid Them

When solving mathematical problems, it’s easy to make mistakes, especially when dealing with complex equations and operations. Recognizing common errors is an essential part of learning, as it helps students refine their problem-solving skills and avoid repeating the same missteps. By understanding where mistakes often occur, learners can develop strategies to ensure accuracy and improve their overall understanding of the subject.

Here are some of the most frequent mistakes and tips on how to avoid them:

• Incorrectly Applying Operations: Confusing addition, subtraction, multiplication, and division can lead to errors in equations. To avoid this, always double-check each operation and follow the order of operations (PEMDAS).
• Forgetting to Distribute: Many students forget to apply distribution when working with parentheses. Remember to distribute terms properly and verify each step before moving forward.
• Neglecting to Simplify: Sometimes, students overlook the importance of simplifying fractions or terms. Always reduce terms to their simplest form whenever possible to avoid unnecessary complexity.
• Misinterpreting Word Problems: Translating word problems into mathematical equations can be challenging. Take time to carefully read and break down the problem before jumping into the solution process.
• Sign Errors: One of the most common mistakes is misplacing negative signs, especially when working with subtraction or multiplication. Keep track of positive and negative numbers to ensure proper results.

By being aware of these common errors and applying corrective strategies, students can significantly reduce mistakes and strengthen their understanding of the material.

Mastering Core Algebra Concepts with Practice

To truly grasp the essential principles of mathematics, consistent practice is key. It’s not enough to simply understand the theory; regular exercises help solidify concepts and improve problem-solving abilities. Practicing a variety of problems reinforces the methods and strategies required to tackle different types of equations, making complex topics more accessible and manageable over time.

Building Confidence Through Repetition

Repetition is one of the most effective ways to master any subject. By regularly working through exercises, students familiarize themselves with patterns, techniques, and approaches to common problems. This not only increases speed and accuracy but also boosts confidence in applying knowledge to new challenges. The more problems a learner tackles, the more intuitive the process becomes.

Fostering Deeper Understanding

Each time a student solves a problem, they refine their understanding of the underlying principles. Practice allows learners to explore different scenarios and adjust their approach based on the specific requirements of each problem. This process deepens comprehension and equips students with the ability to adapt their knowledge to a variety of situations.

How to Use the Answers Effectively

Having access to the correct solutions is only the first step in mastering a subject. To truly benefit from these solutions, it’s important to use them strategically. Simply checking if your answer is right or wrong isn’t enough; the goal is to understand the process that leads to the solution. By examining each step in detail, you can learn how to approach similar problems in the future with confidence.

Analyze Each Step: Instead of just looking at the final result, break down each step of the solution. Understand why each action is taken and how it contributes to reaching the answer. This will help you recognize patterns and strategies that can be applied to other problems.

Identify Mistakes and Learn from Them: If your solution doesn’t match the correct one, use the provided steps to pinpoint where you went wrong. Understanding your mistakes is crucial for avoiding them in the future. By correcting errors and understanding why they occurred, you will strengthen your problem-solving skills.

Practice Similar Problems: Once you’ve reviewed the solution, try solving a similar problem on your own. This reinforces the methods you’ve just learned and helps you internalize the process. Over time, this will make it easier to solve more complex problems independently.

Improving Problem-Solving with Algebra Solutions

Enhancing problem-solving skills requires more than just memorizing formulas or techniques. It’s about developing a deep understanding of the methods used to arrive at solutions. By examining detailed solutions to mathematical challenges, students can identify the key strategies that make complex problems easier to tackle. With each solution, learners gain valuable insights that help improve their ability to approach new problems with clarity and confidence.

Here are some ways that reviewing solutions can enhance problem-solving abilities:

• Understanding the Process: Seeing each step of a solution helps students understand the logical progression needed to solve a problem, making it easier to apply these steps to similar questions.
• Recognizing Patterns: By working through multiple problems, learners start to identify common strategies that work for different types of equations, helping them tackle new problems more efficiently.
• Developing Critical Thinking: Studying solutions helps develop a more analytical mindset, allowing students to think critically about their approach and explore different methods for reaching the correct answer.
• Building Confidence: When students see that they can follow a step-by-step process to solve a problem correctly, it builds confidence and reinforces their understanding of the material.

By consistently reviewing and analyzing solutions, students can strengthen their problem-solving skills, making them more prepared for increasingly difficult challenges.

Key Algebra Topics Covered in the Textbook

This educational resource covers a wide range of important mathematical concepts that provide the foundation for more advanced studies. By exploring these essential topics, students gain the skills and understanding required to solve complex problems effectively. Each section introduces a fundamental area of study, building on previous concepts and helping learners develop a deeper comprehension of the subject.

Below is a table summarizing some of the key areas explored:

Topic	Description
Linear Equations	Methods for solving equations involving variables with a degree of one, using techniques such as substitution and elimination.
Quadratic Equations	Exploration of equations that involve squared terms, and techniques for solving them such as factoring, completing the square, and using the quadratic formula.
Polynomials	Understanding the structure and operations of polynomials, including addition, subtraction, multiplication, and division of terms.
Functions	Introduction to different types of functions, their graphs, and methods for solving equations involving functions.
Slope and Intercepts	Understanding the concept of slope in a line and how to find the x- and y-intercepts in linear equations.
Exponents and Radicals	Exploring the properties of exponents and how to simplify radical expressions and equations.

By mastering these key topics, students are well-equipped to handle more complex mathematical challenges and gain the confidence needed to succeed in future studies.

Understanding Word Problems in Algebra

Word problems can often seem intimidating, but they are an excellent way to apply mathematical concepts to real-world situations. These types of problems require students to translate a written description into a mathematical equation or expression. The key to solving word problems effectively lies in breaking down the information, identifying the variables, and recognizing the relationship between the quantities involved. With practice, learners can develop a systematic approach that turns seemingly complex scenarios into manageable tasks.

Here are some strategies to help understand and solve word problems:

• Read the Problem Carefully: Pay close attention to the wording, and underline or highlight important information. This will help you focus on the key details needed to solve the problem.
• Identify the Unknowns: Determine what the problem is asking for and assign variables to represent these unknowns. This step turns the word problem into a mathematical equation.
• Translate the Words into Equations: Use the information provided in the problem to create an equation. Look for phrases that indicate mathematical operations, such as “sum,” “difference,” “product,” or “quotient.”
• Solve the Equation: Once the equation is set up, solve it using the appropriate methods, whether it’s solving for a variable, simplifying expressions, or using a system of equations.
• Check the Solution: After finding the solution, review the problem to ensure that the answer makes sense in the context of the original scenario. This step helps verify the accuracy of your work.

By consistently practicing word problems, students can improve their ability to think critically and apply mathematical skills to everyday situations. This not only enhances their problem-solving abilities but also builds confidence in using mathematics in practical contexts.

Unlocking Success with Algebra Practice

Success in mathematics is largely determined by consistent practice. The more problems you solve, the stronger your understanding becomes. Regular practice allows you to reinforce concepts, sharpen your problem-solving skills, and identify areas that need improvement. Each problem you tackle builds confidence, making complex tasks feel more manageable over time. It’s not about memorizing formulas, but rather about mastering the process and learning how to apply it in various scenarios.

Here are some key benefits of regular practice:

• Reinforces Concepts: Practicing regularly helps solidify the foundational ideas that support more complex topics, ensuring a deeper understanding of the material.
• Improves Problem-Solving Speed: The more you practice, the quicker and more efficient you become in recognizing patterns and solving problems. This skill is crucial when faced with time-sensitive tests or assignments.
• Boosts Confidence: Success in solving problems gives you the assurance to tackle even more challenging tasks. Each solved problem adds to your mathematical toolkit, preparing you for future challenges.
• Enhances Retention: Repetition is a proven way to retain information. By working through a variety of problems, you not only understand concepts but also remember them for longer periods.

By dedicating time to solving problems regularly, you lay the groundwork for long-term success and gain the ability to approach even the most difficult challenges with confidence and clarity.

Learning Strategies for Algebra Mastery

Mastering mathematical concepts requires more than just understanding the rules; it demands a strategic approach to learning that allows students to apply their knowledge effectively. Success in solving mathematical problems comes from a blend of consistent practice, active engagement, and developing a clear understanding of the underlying principles. By using the right strategies, students can accelerate their progress and develop a solid foundation in mathematics.

Here are some effective learning strategies to achieve mastery:

• Break Down Complex Problems: Instead of tackling an entire problem at once, break it into smaller, more manageable parts. This allows you to focus on one aspect of the problem at a time, leading to a clearer solution.
• Practice Regularly: Frequent practice helps reinforce concepts and build confidence. The more problems you solve, the more proficient you become in recognizing patterns and applying methods effectively.
• Understand the Why: Focus on understanding the logic behind each step rather than just memorizing formulas. When you grasp the reasoning behind mathematical processes, you can apply them in a variety of contexts.
• Use Visual Aids: Diagrams, graphs, and charts can be valuable tools for visualizing complex concepts. These tools help make abstract ideas more concrete and easier to comprehend.
• Collaborate with Others: Working with peers allows you to share insights and approaches to problems. Teaching others what you’ve learned is also an excellent way to reinforce your own understanding.
• Review Mistakes: Mistakes are a natural part of learning. Instead of getting discouraged, review your errors and learn from them. Understanding why an answer was wrong helps prevent similar mistakes in the future.

By implementing these strategies, students can strengthen their problem-solving abilities, improve retention, and approach new challenges with confidence. Mastery of mathematical concepts is not only about solving problems but also about developing the skills to think critically and independently.

How to Tackle Complex Algebra Equations

Complex mathematical equations can seem daunting at first, but with the right approach, they become much more manageable. The key to solving intricate equations lies in breaking them down into simpler steps, identifying patterns, and applying logical strategies. By following a structured method, you can systematically approach and solve even the most challenging expressions.

Step 1: Simplify the Equation

Before diving into complex operations, simplify the equation as much as possible. Look for opportunities to combine like terms, remove unnecessary parentheses, or factor common factors out. The more simplified the equation, the easier it becomes to isolate variables and work through the solution.

Step 2: Use Systematic Methods

Once the equation is simplified, apply systematic methods such as substitution or elimination when solving systems of equations. In single-variable equations, use techniques like the distributive property, inverse operations, or factoring to gradually isolate the variable of interest. Step-by-step progression ensures accuracy and prevents errors in the solution process.

By remaining patient, focusing on one step at a time, and using these strategies, even the most complex equations can be solved with confidence. Practice and persistence are crucial to mastering these techniques and developing the skills needed to approach any problem with clarity.

Algebra Resources Beyond the Textbook

Learning mathematical concepts extends far beyond the classroom textbook. With a variety of online tools, interactive platforms, and supplementary materials, students have access to a wealth of resources that can help strengthen their understanding and improve problem-solving skills. These resources offer different approaches and perspectives, providing alternative explanations and practical applications of mathematical principles.

Below is a list of valuable resources to explore beyond traditional classroom materials:

Resource Type	Description	Examples
Online Tutorials	Video lessons and step-by-step tutorials that break down complex topics into digestible chunks.	Khan Academy, YouTube educational channels
Interactive Tools	Websites and apps that provide hands-on practice and instant feedback on exercises.	Wolfram Alpha, Desmos
Math Forums	Communities where students can ask questions, share solutions, and get advice from peers or experts.	Stack Exchange, Reddit Math Communities
Practice Websites	Platforms offering a vast array of problems to solve, often tailored to specific skills or levels of difficulty.	IXL, Mathway

By utilizing these diverse resources, learners can enhance their skills, clarify doubts, and find creative solutions to problems. Exploring multiple sources of information allows students to approach challenges from different angles, deepening their understanding and boosting confidence in their abilities.

Real-World Applications of Algebra

Mathematical concepts are not confined to the classroom–they are widely used in everyday life and across various industries. From budgeting to engineering, the skills learned through solving equations have real-world applications that help solve problems and make informed decisions. Understanding how these principles apply outside of academic settings makes learning more relevant and shows the value of mathematical thinking in practical scenarios.

Below are some areas where mathematical problem-solving is essential:

• Finance and Budgeting: Managing personal finances, calculating interest rates, and planning investments all rely on understanding equations and ratios.
• Engineering and Architecture: Design and construction projects involve using mathematical models to ensure structural integrity, calculate dimensions, and estimate material costs.
• Technology and Computer Science: Algorithms, data analysis, and software development all require a strong understanding of mathematical principles to optimize processes and enhance functionality.
• Medicine and Health: Analyzing data trends, calculating dosages, and interpreting medical test results often require mathematical computations to make accurate decisions.
• Environmental Science: Studying patterns in climate change, resource management, and population dynamics all involve mathematical modeling to predict outcomes and assess solutions.

By applying mathematical techniques to solve real-world challenges, students gain a deeper appreciation for the subject and understand its importance in solving both everyday and complex problems. These practical applications demonstrate how math can shape industries, improve lives, and drive innovation across the globe.

Assessing Your Progress in Algebra

Tracking your development in mathematical problem-solving is essential for identifying strengths and areas that need improvement. Regular assessments help you gauge how well you understand key concepts, and they provide valuable insights into where further practice or review might be necessary. Whether you’re working through exercises on your own or engaging with instructional materials, measuring your progress allows for more focused and effective learning.

Here are some effective methods to assess your growth in solving mathematical problems:

• Self-Testing: Regularly completing practice problems is one of the best ways to test your understanding. If you can solve them correctly, it’s a sign that you’re mastering the material. If you struggle, it might indicate the need to review specific topics.
• Reviewing Mistakes: Mistakes offer valuable learning opportunities. Analyzing where you went wrong helps identify gaps in your understanding and prevents repeating those errors in future problems.
• Peer Discussions: Engaging with others on challenging problems can help clarify difficult concepts. Discussing various approaches provides new perspectives and deepens your understanding.
• Timed Quizzes: Completing problems within a set time frame helps improve both speed and accuracy. Timed exercises simulate test conditions and teach you how to approach problems efficiently under pressure.
• Progress Tracking: Keeping a record of your practice results over time allows you to monitor improvement. It can also highlight areas that need more attention, ensuring consistent growth.

Regularly assessing your performance is not just about testing knowledge but about recognizing patterns in your learning journey. By consistently evaluating your abilities, you can identify when a topic is fully understood and when further practice is necessary. This ongoing self-reflection will support steady progress and help build confidence in solving complex problems.

Improving Skills with Regular Review

Consistent practice and review are fundamental to mastering mathematical techniques and problem-solving methods. Without revisiting past material, it’s easy to forget important steps and concepts. Regularly going over previously learned topics helps reinforce understanding, identify weak areas, and build long-term retention. A steady review schedule can significantly enhance proficiency and confidence in solving complex problems.

Here are several strategies for improving skills through regular review:

• Scheduled Sessions: Setting aside dedicated time for review each week helps keep concepts fresh and ensures continuous progress. Even short review sessions can make a big difference in long-term retention.
• Active Recall: Instead of passively rereading notes, try to recall key formulas and methods from memory. This active process strengthens neural connections and makes information more accessible when needed.
• Mixing Old and New Content: Combine current topics with earlier ones to see how different concepts interconnect. This helps build a deeper understanding and improves your ability to apply knowledge across a range of problems.
• Practice with Variations: Solve problems with varying levels of difficulty. Tackling a wide range of examples forces you to adapt and apply the concepts in different ways, which enhances your problem-solving skills.
• Using Resources: Utilize additional resources like online tutorials, interactive exercises, or peer study groups to review challenging concepts. Diverse methods of learning can offer new insights and make the review process more engaging.

By making review an ongoing part of your learning routine, you’ll not only reinforce what you’ve already mastered but also stay better prepared for tackling new challenges. The key to success is consistency and a proactive approach to revisiting concepts, ensuring that the knowledge becomes second nature over time.