Eureka Math Grade 3 Module 2 Answer Key

In the third grade, students encounter a variety of new and challenging concepts that lay the foundation for future academic success. This section provides essential tools for mastering the lessons, helping learners progress confidently through their studies.
By reviewing detailed explanations and step-by-step solutions, students can clarify their understanding and tackle complex problems with ease. Each topic is designed to reinforce critical thinking skills and promote problem-solving strategies that will serve them well in future learning.
Whether you’re looking for guidance on a specific problem or seeking a deeper understanding of the material, this resource is here to support both students and educators alike. Mastering these concepts is key to building a solid mathematical foundation and achieving long-term success in academic endeavors.
Eureka Math Grade 3 Module 2 Answer Key
In this section, you’ll find detailed solutions to help navigate the third-grade curriculum. These solutions are designed to provide clarity and support for students as they work through the various challenges presented in their lessons. The focus is on reinforcing understanding and ensuring that each step is explained thoroughly, enabling learners to grasp important concepts with confidence.
Each problem is broken down into manageable parts, allowing students to see how the solutions are derived. By working through these steps, students will develop stronger analytical skills and a deeper understanding of the content. This section is intended not only to clarify the correct responses but also to teach valuable problem-solving techniques that can be applied to future learning experiences.
Whether you’re revisiting a tricky concept or seeking to verify your work, these resources will guide you through each process with clear and easy-to-follow instructions. The goal is to ensure students can tackle similar challenges independently, laying the groundwork for more advanced topics in the future.
Overview of Eureka Math Grade 3
The third-year curriculum in mathematics focuses on building a strong foundation for essential concepts that will be crucial for higher learning. This stage introduces new topics, while reinforcing previously learned skills, helping students develop a deep understanding of numbers, operations, and problem-solving techniques. Throughout this stage, the emphasis is on applying learned concepts to solve practical challenges and strengthen logical reasoning abilities.
Core Concepts in the Third-Year Curriculum
- Understanding place value and how it relates to addition and subtraction.
- Developing proficiency in multiplication and division of larger numbers.
- Solving word problems and applying learned techniques to real-world situations.
- Identifying and using fractions as parts of a whole.
- Exploring measurements, including units of length, weight, and volume.
Skills Developed Throughout the Year
- Increased ability to work with larger numbers and multi-step operations.
- Enhanced problem-solving skills through practice with word problems and mathematical reasoning.
- Improved understanding of geometric shapes, spatial relationships, and measurement concepts.
- Strengthened ability to represent numbers using various methods like arrays and number lines.
This stage prepares students for more advanced topics by encouraging independent thinking and the ability to tackle mathematical problems in creative ways. By the end of the year, students should have a strong grasp of basic concepts, ready to approach more complex challenges in subsequent lessons.
Key Concepts in Module 2

In this section, students delve into important foundational ideas that help expand their understanding of basic number operations. The concepts covered are designed to strengthen their ability to apply learned strategies to solve problems more effectively. A key focus is on enhancing both computational skills and conceptual thinking.
Place value plays a crucial role, as students develop a deeper understanding of how digits within a number relate to each other. This concept forms the basis for more complex operations and allows students to perform addition and subtraction with larger numbers accurately.
Multiplication and division become central skills in this stage, with students learning how to approach problems involving multiple steps and larger values. The emphasis is placed on understanding how these operations relate to each other, building a stronger connection between addition, subtraction, multiplication, and division.
Additionally, problem-solving strategies are introduced, encouraging students to approach real-world challenges with critical thinking. The ability to interpret and solve word problems is developed through practice, helping students connect mathematical knowledge with everyday scenarios.
Importance of Understanding Module 2
Grasping the key concepts in this section is essential for building a solid foundation in numeracy. As students progress, the skills developed here serve as the building blocks for more complex topics in the future. Mastery of these ideas enhances both problem-solving abilities and computational accuracy, ensuring long-term academic success.
Benefits of Mastering Core Concepts
Understanding the lessons in this section not only prepares students for upcoming challenges but also reinforces their overall confidence in handling mathematical tasks. The following table highlights the main advantages of mastering these concepts:
| Skill | Benefit |
|---|---|
| Place Value Understanding | Improves ability to perform operations with larger numbers. |
| Multiplication and Division Fluency | Strengthens basic arithmetic and supports future calculations. |
| Problem-Solving Techniques | Enhances critical thinking skills and real-world application. |
Real-World Applications

Mastery of these concepts not only benefits academic performance but also translates into everyday situations. Understanding how to work with numbers, solve problems, and think critically can help students excel beyond the classroom in various real-life contexts.
How to Use the Answer Key Effectively
Using a solution guide correctly can be a powerful tool for reinforcing learning and improving problem-solving skills. However, it’s important to approach it strategically, ensuring that it serves as a guide for understanding the material rather than just a quick reference for answers. By reviewing each solution in detail and applying the process to similar problems, students can develop a deeper comprehension of the concepts involved.
Steps for Effective Use
Follow these steps to maximize the benefits of using the solution guide:
| Step | Action |
|---|---|
| 1 | Attempt problems on your own before checking the solutions. |
| 2 | Use the guide to verify your answers, ensuring you understand each step. |
| 3 | Review the explanations to see where you may have gone wrong and how to correct it. |
| 4 | Practice similar problems to reinforce your understanding of the concepts. |
Common Mistakes to Avoid
While using the guide can be helpful, it’s important to avoid using it as a shortcut. Relying too heavily on the solutions can hinder independent thinking and problem-solving development. Make sure to use the guide as a learning tool rather than as a way to simply confirm answers.
Step-by-Step Solutions for Module 2
In this section, we break down the problems from this stage into clear, manageable steps. Each solution is presented in a way that helps reinforce the key concepts and ensures a deeper understanding of the process behind each calculation. By following these steps, students can build confidence and learn how to approach similar challenges independently.
Example 1: Solving a Multi-Step Problem
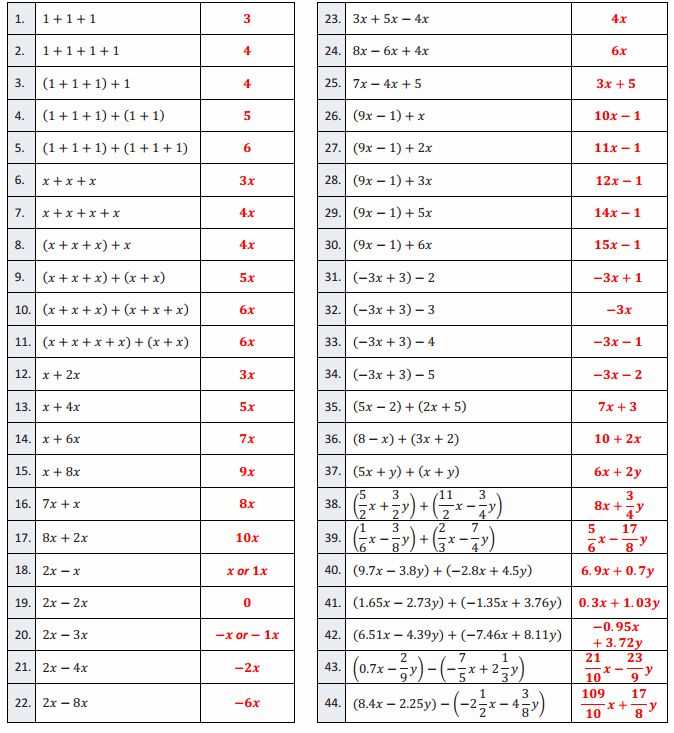
Let’s take a look at an example problem and solve it step-by-step:
- Read the problem carefully: Identify the numbers involved and what is being asked.
- Break the problem into parts: Separate the steps and solve each one individually.
- Perform the necessary calculations: Use addition, subtraction, multiplication, or division as needed.
- Check the work: Review each step to make sure all calculations are correct and align with the problem.
- Write the final solution: State the answer clearly, ensuring it answers the question posed in the problem.
Example 2: Working with Fractions
For problems involving fractions, follow these steps:
- Identify the fractions: Look for numerators and denominators.
- Find a common denominator: If adding or subtracting fractions, ensure the denominators are the same.
- Perform the operation: Add, subtract, multiply, or divide as required by the problem.
- Simplify the result: If necessary, reduce the fraction to its simplest form.
- Verify the solution: Double-check the final result to ensure accuracy.
By working through each problem step-by-step, students gain a thorough understanding of the methods used, helping them approach similar problems with confidence in the future.
Common Mistakes in Module 2
While working through the lessons in this section, students often encounter a few common errors that can lead to confusion and incorrect results. Understanding these mistakes and learning how to avoid them is essential for mastering the concepts and developing strong problem-solving skills. Below, we highlight some of the most frequent pitfalls and provide tips on how to avoid them.
1. Misunderstanding Place Value
A frequent mistake occurs when students misinterpret the value of digits in larger numbers. This often happens during addition or subtraction, where students may incorrectly align the digits, leading to errors in their calculations. Ensuring that each digit is placed correctly according to its value is crucial for accuracy. Practice with number charts or visual aids can help reinforce this concept.
2. Confusing Multiplication and Division
Another common mistake is mixing up multiplication and division. Since these operations are closely related, students sometimes forget to switch between the two when solving word problems. To avoid this mistake, it’s helpful to read the problem carefully, identify the operation needed, and double-check the mathematical relationship between the numbers before proceeding.
By recognizing these common errors and taking the time to correct them, students can significantly improve their accuracy and confidence in solving similar problems in the future.
Tips for Solving Module 2 Problems
Successfully tackling problems in this section requires a strategic approach and a solid understanding of the core concepts. By following a few helpful tips, students can improve their problem-solving skills, reduce mistakes, and gain more confidence in their abilities. Below are some effective strategies to keep in mind when working through various exercises.
1. Break Down the Problem
Before jumping into calculations, take time to carefully read and analyze the problem. Breaking it into smaller, manageable steps can help avoid confusion. Here’s how you can approach any problem:
- Identify what is being asked: Understand the goal of the problem.
- Highlight key information: Look for numbers, units, and relevant details.
- Plan your approach: Decide which operations you need to perform.
2. Double-Check Your Work
After completing a problem, always review your calculations. Errors are common, especially when working with larger numbers or multiple steps. Take a moment to:
- Check each operation step by step.
- Ensure that numbers are placed correctly.
- Revisit the problem to confirm that your solution answers the original question.
3. Use Visual Aids
For many problems, especially those involving fractions or large numbers, drawing a visual representation can make understanding easier. Diagrams, number lines, or fraction bars can be very helpful tools for visualizing and solving problems more effectively.
By following these strategies, students can approach problems with more confidence, making fewer mistakes and better understanding the material as they progress through each task.
Understanding the Lessons in Module 2
The lessons in this section are designed to build a strong foundation in key concepts and problem-solving strategies. Each lesson progresses logically, starting with basic principles and advancing to more complex ideas. To fully understand the material, it’s important to focus on each lesson individually while also seeing how they connect to each other. By grasping the core concepts, students can approach problems with a clearer understanding and greater confidence.
Key Concepts Covered in Each Lesson
Below is a breakdown of the main topics covered in the lessons of this section:
| Lesson | Focus Area |
|---|---|
| Lesson 1 | Introduction to basic operations and understanding place value. |
| Lesson 2 | Building fluency with addition and subtraction. |
| Lesson 3 | Applying concepts to solve multi-step problems. |
| Lesson 4 | Introduction to working with fractions. |
| Lesson 5 | Understanding and applying word problems effectively. |
As you work through each lesson, take the time to review examples and practice exercises. This will ensure a deeper understanding of the material and provide a solid foundation for more advanced topics in the future.
How Module 2 Builds on Previous Knowledge
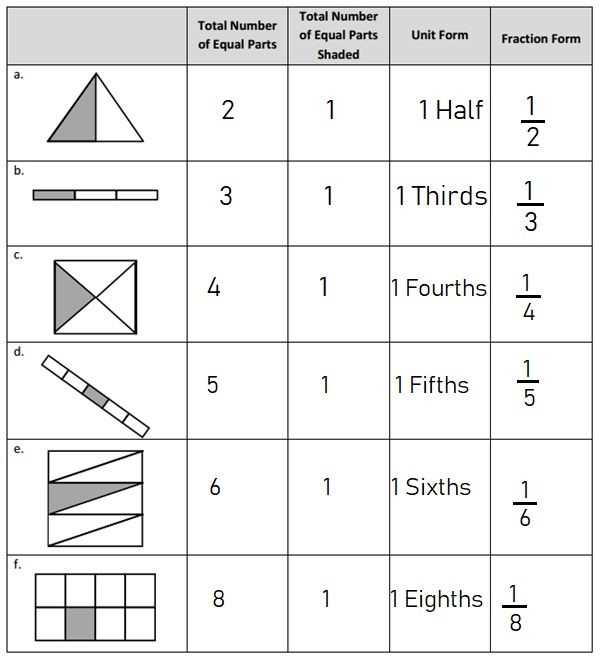
This section is designed to help students strengthen their understanding of foundational concepts while introducing new skills. The lessons gradually expand on what has been previously learned, reinforcing earlier ideas and providing new tools to solve more complex problems. By making connections between past knowledge and new material, students are able to build a more solid and integrated understanding of the subject.
For example, earlier lessons may introduce basic operations such as addition and subtraction. In this section, students deepen their understanding by applying these operations to larger numbers and more advanced scenarios. The key is to continuously revisit and practice these core skills in different contexts, ensuring a solid grasp of the basics before moving on to more challenging tasks.
By using prior knowledge as a stepping stone, students gain confidence in their abilities, enabling them to tackle more advanced problems and make connections between different mathematical ideas. This approach fosters a more comprehensive understanding of the subject and helps students see how their learning builds progressively over time.
Answer Key for Word Problems in Module 2
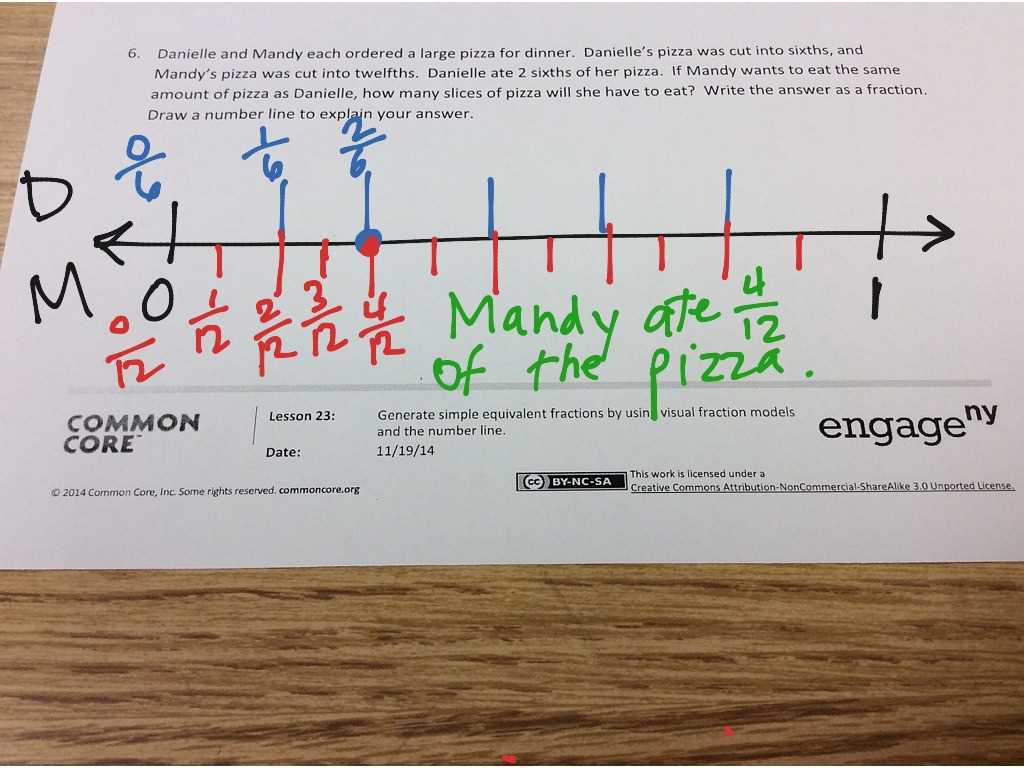
Word problems are an essential part of learning, as they help students apply their knowledge to real-world situations. In this section, we will provide solutions and step-by-step explanations for the word problems covered. By understanding the approach to each problem, students can learn how to break down complex scenarios into manageable steps and solve them with confidence.
Problem 1: Shopping at the Store
Example Problem: Emily went to the store and bought 3 packs of pencils. Each pack costs $2. How much did she spend in total?
Solution: To solve this problem, multiply the cost of one pack by the number of packs bought:
- Cost per pack = $2
- Number of packs = 3
- Total cost = 3 × 2 = $6
Emily spent $6 in total.
Problem 2: Sharing Cookies
Example Problem: There are 12 cookies, and 4 friends want to share them equally. How many cookies will each friend get?
Solution: To divide the cookies equally, divide the total number of cookies by the number of friends:
- Total cookies = 12
- Number of friends = 4
- Cookies per friend = 12 ÷ 4 = 3
Each friend will get 3 cookies.
By following these examples and understanding the reasoning behind each calculation, students will gain a clearer understanding of how to approach and solve similar word problems on their own.
Visual Aids for Module 2 Problems

Visual aids play an important role in helping students grasp complex concepts by providing clear, tangible representations of abstract ideas. For the problems in this section, illustrations, charts, and diagrams can help break down the steps and offer a more intuitive understanding of the process. By using these tools, students can better visualize how to approach and solve problems, which enhances their overall learning experience.
Using Diagrams for Word Problems
When solving word problems, drawing a diagram can make a big difference. For example, in a problem about sharing items or grouping things, a simple visual of the objects can help students understand how to divide them or calculate totals. Below is an example of how a diagram can help clarify a problem:
- Problem: There are 15 apples, and we need to divide them equally between 3 baskets.
- Solution: Drawing 3 baskets with 15 apples inside helps visualize the equal division.
Using Number Lines for Operations
Number lines are a great tool for visualizing addition, subtraction, and other operations. By plotting numbers on a line, students can more easily see how values increase or decrease based on the operation being performed. For example:
- Problem: Add 7 to 3.
- Solution: A number line shows that starting at 3, moving 7 steps forward reaches 10.
These visual tools support students in understanding how numbers and operations work, making problem-solving easier and more effective.
Practice Exercises for Mastery
Mastery of any skill requires consistent practice and reinforcement of concepts. In this section, we provide a series of practice exercises designed to help students strengthen their understanding of the material. These exercises focus on applying the techniques and methods learned, ensuring that students gain confidence and proficiency in solving problems on their own.
Exercise 1: Basic Operations
Start by practicing basic operations to solidify your understanding of core concepts. Try the following:
- Problem 1: Add 56 and 29.
- Problem 2: Subtract 78 from 124.
- Problem 3: Multiply 9 by 7.
- Problem 4: Divide 144 by 12.
Exercise 2: Word Problems
Once you’re comfortable with the basic operations, move on to word problems that require applying your skills in real-life scenarios. These problems help connect the abstract with the concrete:
- Problem 1: Sarah has 5 baskets, and each basket contains 12 oranges. How many oranges does Sarah have in total?
- Problem 2: A bookstore sold 45 books on Monday and 30 books on Tuesday. How many books did they sell in total over the two days?
- Problem 3: If a pack of pencils costs $3 and you buy 4 packs, how much do you spend?
Completing these exercises will help reinforce the key concepts and techniques necessary to achieve mastery. Remember to review your work and identify areas for improvement as you progress.
Resources to Complement the Answer Key
In addition to the provided solutions, various resources can further enhance the learning experience and provide additional support. These materials are designed to help reinforce concepts, offer alternative explanations, and give students extra opportunities to practice. By utilizing these resources, learners can deepen their understanding and improve their skills more effectively.
Some valuable resources to complement your study process include:
- Interactive Websites: Websites that offer interactive problem-solving and step-by-step guidance can help students apply concepts in real-time. These sites often provide immediate feedback, which aids in better retention and understanding.
- Worksheets and Practice Sheets: Printable worksheets are a great way to practice skills offline. They often include a variety of problem types, giving students a broader set of challenges to work through.
- Educational Videos: Visual learners can benefit from watching videos that explain complex concepts in a clear and engaging way. These videos often include animated examples that help break down difficult topics.
- Study Groups: Collaborating with peers in study groups provides the opportunity for group discussions and problem-solving. Explaining concepts to others can reinforce one’s own understanding and address any confusion.
- Teacher or Tutor Assistance: For personalized help, seeking guidance from a teacher or tutor can be invaluable. They can offer tailored support and explain tricky areas that may need extra attention.
By combining these resources with your work, you’ll have access to a well-rounded set of tools that support mastery and boost overall performance.
How Parents Can Support Learning
Parents play a crucial role in enhancing their child’s educational experience. By creating a supportive environment, being involved in their child’s learning process, and offering encouragement, parents can help build confidence and foster a love for learning. Simple actions taken at home can significantly impact a child’s academic growth and development.
Here are a few ways parents can effectively support their child’s learning:
- Provide a Consistent Routine: Establishing a structured schedule helps children stay organized and focused. Consistent study times and breaks allow for a balanced learning environment.
- Engage in Active Discussions: Talking with children about what they’re learning helps them process information more deeply. Ask open-ended questions to encourage critical thinking and reflection on the topics covered.
- Create a Positive Study Space: A quiet, distraction-free area dedicated to studying enhances concentration and productivity. Make sure the space is well-lit, organized, and equipped with necessary materials.
- Offer Encouragement and Praise: Positive reinforcement motivates children to keep working hard. Praise their efforts and celebrate their successes, no matter how small. This builds self-esteem and perseverance.
- Be a Resource for Assistance: If your child is struggling with a concept, offer guidance or suggest seeking additional help from teachers or tutors. Providing emotional support and reassurance is just as important as academic help.
By being proactive and supportive, parents can make a significant difference in their child’s educational journey. The involvement and encouragement from parents contribute to a positive learning experience and can help students achieve their full potential.
Reviewing Key Skills from Module 2
In any educational journey, it is essential to review and reinforce the fundamental concepts that students learn. By revisiting key skills, learners solidify their understanding and ensure a strong foundation for future topics. Reviewing the core concepts from this section allows students to grasp the material more thoroughly and gain confidence in applying their knowledge to new challenges.
Some of the important skills covered include:
- Problem-Solving Strategies: Students are encouraged to break down complex problems into smaller, manageable steps. This skill helps them approach a variety of challenges with confidence and clarity.
- Understanding Relationships Between Numbers: Emphasis is placed on recognizing patterns and relationships between different numerical concepts. This enables students to see how numbers interact and form connections.
- Critical Thinking and Reasoning: Developing the ability to analyze problems critically and logically is crucial for success in future learning. Students are taught to evaluate situations, make inferences, and draw conclusions based on evidence.
- Application of Basic Operations: A solid understanding of the basic operations–addition, subtraction, multiplication, and division–is essential. Mastery of these allows students to tackle more advanced concepts with ease.
- Visualization and Representation: Using visual aids like diagrams, charts, and number lines helps students better understand abstract concepts and see the relationships between different mathematical ideas.
By reviewing and practicing these essential skills, students are better prepared to move forward in their learning journey with confidence and mastery. It is vital to continue reinforcing these skills regularly to ensure long-term retention and success.