Algebra Final Exam Answer Key for Effective Study

Understanding the concepts and problem-solving techniques is essential when preparing for any math assessment. Having access to a comprehensive guide can provide students with the tools to reinforce their knowledge and build confidence before tackling challenging questions.
In this section, we explore resources that assist in checking and confirming the steps taken during problem-solving. These materials aim to provide clarity and offer an organized way to evaluate your understanding of key mathematical principles.
By carefully reviewing provided solutions and practicing similar problems, learners can develop a deeper comprehension of their strengths and areas needing improvement. This process not only helps in mastering complex problems but also enhances overall problem-solving skills for future use.
Algebra Final Exam Answer Key
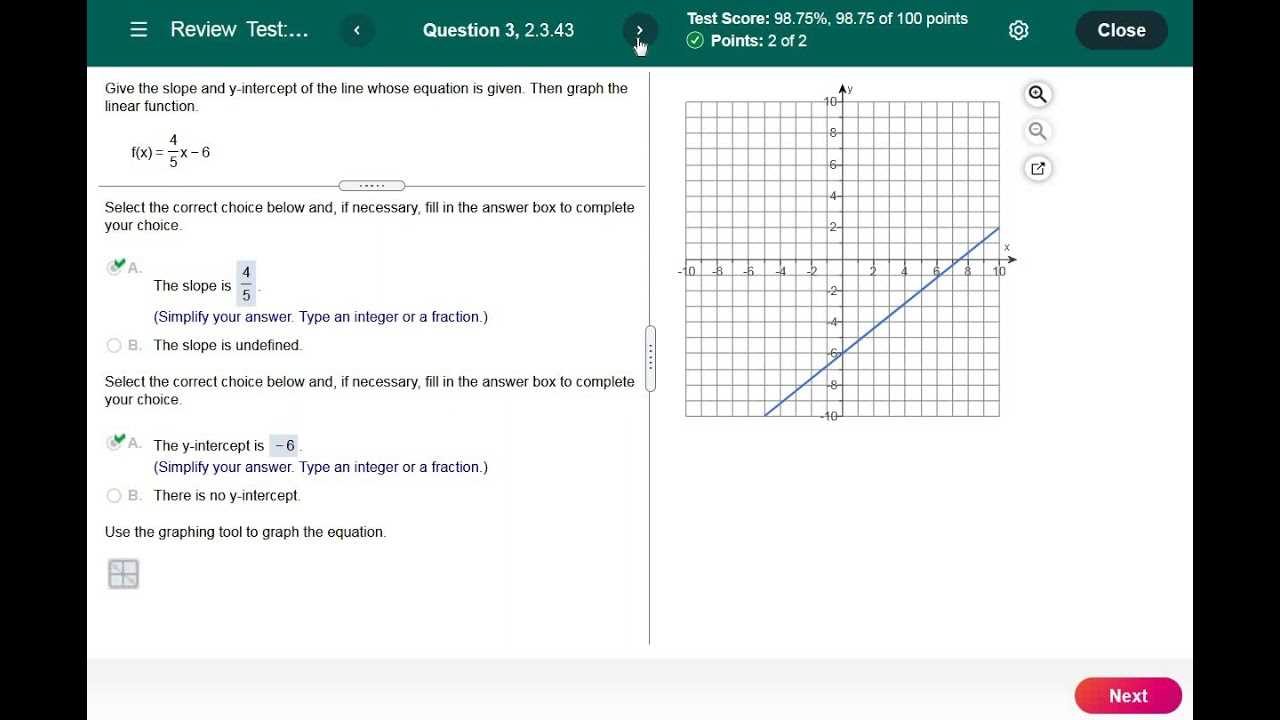
Having a detailed set of solutions to refer to can be incredibly beneficial when reviewing complex mathematical problems. It serves as a guide to check your calculations and verify that each step aligns with the expected results. This not only boosts your confidence but also helps to identify areas where further practice may be needed.
How to Use the Provided Solutions
When reviewing solutions, consider the following strategies for effective learning:
- Compare your approach to the provided solutions to identify any discrepancies.
- Pay attention to the methods used to solve the problems, ensuring you understand the rationale behind each step.
- Use the solutions to clarify any misunderstandings from practice problems.
Benefits of Referencing Solutions
Referring to a well-structured set of solutions offers several advantages:
- Improved understanding: Clarifies complex concepts and reinforces learning.
- Accuracy check: Helps you ensure all steps were completed correctly and nothing was missed.
- Efficient study: Reduces time spent on trial and error, allowing you to focus on areas requiring more attention.
By carefully analyzing the provided solutions and applying them to similar problems, you can strengthen your problem-solving abilities and be better prepared for future assessments.
Why Use an Answer Key?
Having access to a comprehensive solution guide can significantly enhance your learning process. It acts as a reference to double-check your work, ensuring that each step in the problem-solving process aligns with the correct methods and expected results. This approach not only helps verify accuracy but also offers an opportunity to understand alternative methods of reaching the same solution.
Understanding the Importance of Verification
Verification is crucial when studying any complex subject. By using a solution guide, you can:
- Confirm that all steps are correctly executed and no important calculations are missed.
- Learn the most efficient methods for solving problems, which can be especially helpful for future tasks.
- Identify common errors and understand how to avoid them in future exercises.
Building Confidence and Reducing Anxiety
Knowing that you can cross-check your work provides a sense of assurance. This builds confidence, especially when faced with challenging problems. Furthermore, it helps reduce anxiety, allowing you to approach similar problems with greater ease in the future.
How to Use the Answer Key Effectively
To get the most out of a solution guide, it’s important to approach it strategically. Simply looking at the solutions is not enough; understanding the reasoning behind each step and comparing it with your own approach will lead to better comprehension and retention. Effective use of the solution guide can help reinforce concepts and improve your problem-solving skills.
Step-by-Step Comparison
Start by solving the problems on your own, then refer to the solution guide to see how your approach matches or differs. Focus on:
- Identifying where your solutions align with the provided steps.
- Understanding the logic behind any differences and learning from mistakes.
- Using the guide to clarify any unclear steps in your own process.
Tracking Progress and Learning Patterns
Using a solution guide consistently allows you to track improvements and identify areas for further study. Keep a record of:
| Problem Number | Your Solution | Guide Solution | Notes for Improvement |
|---|---|---|---|
| 1 | Correct | Correct | Keep practicing similar problems |
| 2 | Incorrect | Correct | Review calculation methods |
This method not only helps improve accuracy but also makes it easier to focus on areas that need additional practice, leading to more efficient learning.
Common Mistakes to Avoid

When solving complex mathematical problems, it’s easy to make simple errors that can lead to incorrect results. Recognizing and avoiding these common mistakes is crucial for improving accuracy and ensuring that your calculations are correct. By understanding where these errors typically occur, you can refine your approach and boost your confidence.
Typical Errors in Problem Solving
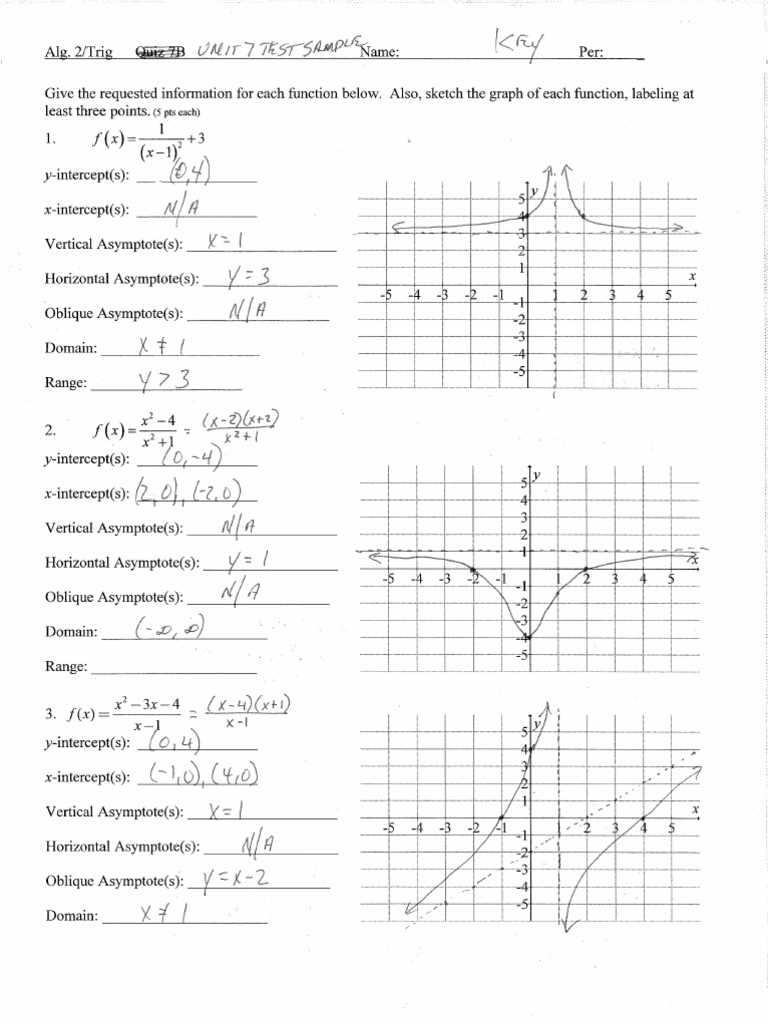
Some of the most frequent mistakes involve misinterpretation of the problem or incorrect application of formulas. Keep an eye on the following:
- Incorrectly applying operations: Forgetting to follow the correct order of operations or making mistakes with negative signs.
- Overlooking terms: Failing to account for all variables or constants in an equation.
- Simple calculation errors: Miscalculating basic arithmetic steps, especially when working with fractions or decimals.
- Sign errors: Mixing up positive and negative signs when performing additions or subtractions.
How to Avoid These Pitfalls
To avoid these common pitfalls, consider these strategies:
- Double-check your calculations, especially in multi-step problems.
- Break down complex equations into smaller, more manageable parts to ensure you haven’t missed anything.
- Use a systematic approach, always following the correct order of operations.
- Take your time to re-read the problem and verify that you’re applying the correct methods.
By being aware of these mistakes and taking proactive steps to avoid them, you can improve both your understanding and your accuracy when solving mathematical problems.
Top Tips for Exam Preparation
Preparing for a challenging assessment requires more than just reviewing material. It’s about adopting effective strategies to enhance understanding, retain key concepts, and build confidence in your abilities. By following certain tips and focusing on specific areas, you can make the preparation process more efficient and productive.
First, focus on mastering the foundational concepts before tackling more complex problems. Make sure you understand the core principles, as this will make solving advanced questions much easier. Next, practice consistently. The more problems you solve, the more familiar you’ll become with the types of questions that may appear.
Lastly, ensure you manage your time wisely during preparation. Create a study schedule that allows you to review different topics each day while leaving enough time to revisit challenging areas. By spacing out your study sessions, you can retain more information and avoid last-minute cramming.
Understanding the Key Concepts in Mathematics
Grasping the fundamental principles is essential for solving mathematical problems with confidence. These core concepts form the building blocks for more complex topics, and understanding them thoroughly ensures success in various problem-solving scenarios. A solid foundation in these ideas not only aids in completing exercises accurately but also helps in applying learned methods to new challenges.
Core Principles to Master
Focus on the following critical concepts to build a strong understanding:
- Equations and Expressions: Learn how to manipulate and solve equations and simplify expressions.
- Factoring: Understand the process of breaking down expressions into their simplest components.
- Variables and Constants: Distinguish between variables, constants, and coefficients, and how they interact in mathematical relationships.
Practical Tips for Mastery
To strengthen your grasp of these principles, consider the following strategies:
- Practice regularly: Solve problems of varying difficulty to reinforce your understanding.
- Seek clarification: Don’t hesitate to ask for help when certain concepts seem unclear.
- Use visual aids: Diagrams or graphs can help you understand relationships between variables and equations.
Mastering these concepts will not only improve your problem-solving skills but also give you the confidence to approach more advanced topics with ease.
How to Check Your Work
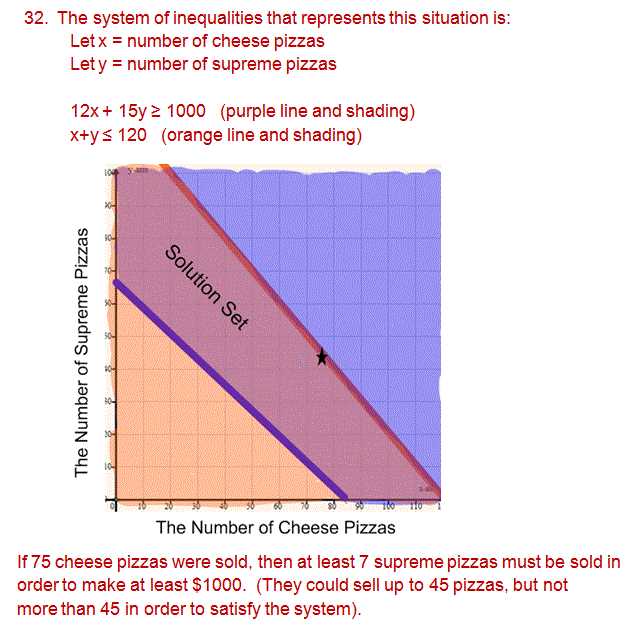
Reviewing your work is a crucial step in ensuring accuracy and preventing simple mistakes from affecting your results. By systematically going through each part of the problem-solving process, you can verify that all steps were executed correctly and that the final solution makes sense. This practice not only improves precision but also builds confidence in your abilities.
Steps to Verify Your Solution
Follow these steps to ensure that your work is correct:
- Recheck calculations: Go over each mathematical operation to confirm that no arithmetic errors were made.
- Review problem setup: Ensure that the correct equation or formula was used at the start.
- Compare with known results: If possible, check your solution against expected or known values to see if they match.
Methods for Double-Checking
Use these techniques to cross-check your answers:
- Reverse the process: Work backwards from your solution to see if it leads you back to the original problem.
- Use different methods: Solve the problem in a different way or use an alternative formula to confirm consistency.
- Ask for feedback: If you are unsure, ask a peer or tutor to review your work.
Taking the time to check your work carefully can help you catch errors before they become problems and ensure that you arrive at the correct solution every time.
Reviewing Practice Problems for Success
Consistent practice is essential for mastering any subject, and reviewing practice problems is a key component of effective learning. By regularly solving a variety of problems, you can reinforce your understanding and become familiar with different problem types. The process of reviewing helps identify areas of weakness and ensures that you are fully prepared for more complex challenges.
It’s important not just to solve the problems but to carefully analyze your solutions. Focus on understanding the logic behind each step and learn from any mistakes. This active review process helps solidify your skills and boosts your confidence in handling similar tasks in the future.
Effective Strategies for Review
When reviewing practice problems, consider these strategies to improve your retention and problem-solving abilities:
- Break down each problem: Take the time to understand each step involved, even if the solution seems simple.
- Focus on different types: Practice problems of varying difficulty and topics to ensure you’re well-prepared for all situations.
- Track your progress: Keep a log of problems you’ve solved correctly and incorrectly to focus on areas that need improvement.
How to Maximize Practice Sessions
To get the most out of your practice, use the following techniques:
- Review mistakes: Go over incorrect solutions to identify where you went wrong and make necessary adjustments.
- Ask for feedback: Have a teacher, tutor, or peer review your work to gain insights and new perspectives.
- Simulate real conditions: Try to solve problems without looking at hints or solutions to better mimic testing environments.
By making practice an integral part of your preparation and focusing on continuous improvement, you can build the skills needed to succeed in any mathematical task.
Benefits of Solving Algebraic Equations
Solving equations is a fundamental skill that enhances problem-solving abilities and sharpens logical thinking. By regularly working with equations, you improve your ability to think critically and approach complex challenges methodically. This practice not only boosts mathematical proficiency but also helps develop skills that are applicable in various real-world situations, such as decision-making and data analysis.
When you solve equations, you are not just manipulating numbers and symbols; you are training your brain to recognize patterns, test hypotheses, and find efficient solutions. This process encourages persistence and attention to detail, qualities that are beneficial beyond the classroom.
Key Advantages of Mastering Equations
Here are some key benefits you can gain from solving equations:
- Improved Critical Thinking: Working through equations helps develop the ability to break down complex problems into simpler steps.
- Enhanced Problem-Solving Skills: Equations often require creative approaches to find solutions, fostering innovative thinking.
- Stronger Analytical Abilities: Solving equations enhances your ability to interpret and analyze information logically and systematically.
How Solving Equations Benefits Other Areas
The skills you acquire from solving equations extend far beyond math-related tasks:
- Application in Finance: The ability to solve equations is useful when managing budgets, calculating interest, or analyzing financial data.
- Boosting Career Opportunities: Many fields, such as engineering, economics, and technology, rely on mathematical reasoning, making these skills highly transferable.
- Better Everyday Decision Making: The logical approach developed through solving equations can be applied to making informed decisions in daily life.
In summary, solving equations provides numerous benefits that enhance your overall cognitive abilities, helping you both academically and in various professional or personal contexts.
How the Answer Key Can Boost Confidence

Having a reliable reference to check your solutions can significantly enhance your self-assurance when tackling complex problems. By reviewing the correct steps and outcomes, you can verify that your approach was sound and your solution was accurate. This process not only reinforces your understanding but also helps to eliminate any lingering doubts about your abilities.
When you have the opportunity to compare your results with the correct ones, it serves as both a reassurance and a learning tool. Even if you made mistakes, seeing the correct methodology allows you to understand where things went wrong and how to improve in the future.
How It Enhances Understanding
Using a reference to check your work has several benefits that can deepen your comprehension:
- Clarifies Misunderstandings: Identifying errors helps pinpoint areas that need further attention, making it easier to grasp complex concepts.
- Reinforces Learning: Repeating problems and checking your solutions solidifies your memory and understanding of key concepts.
- Builds Confidence: Consistently finding that your solutions are correct boosts your self-esteem and encourages a positive learning mindset.
Practical Advantages of Verification
Checking your work with a reference also provides practical advantages:
- Lessens Anxiety: Knowing that you can verify your work reduces feelings of uncertainty and stress.
- Prepares for Future Challenges: Gaining confidence through successful verification equips you to face more difficult problems with confidence.
- Encourages Independent Learning: Being able to self-check fosters autonomy, allowing you to learn and grow without needing constant external support.
Ultimately, having a tool for verifying your work can turn doubts into positive learning opportunities, increasing both your knowledge and confidence in solving similar problems in the future.
Time Management Strategies for Your Exam
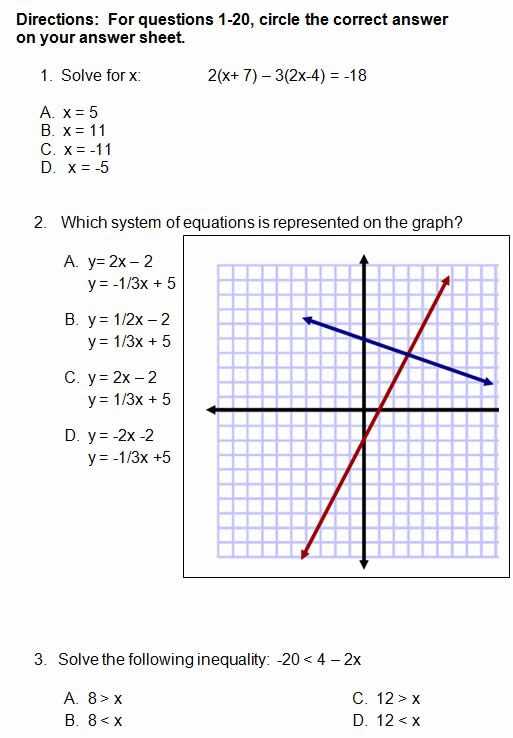
Effective time management during a test is essential for maximizing your performance and minimizing stress. By planning how to allocate your time, you ensure that you can tackle each question with focus and avoid rushing through the later parts. The key is to approach the entire test with a clear strategy that allows you to prioritize tasks, manage your energy, and stay on track throughout the session.
With proper preparation and time allocation, you can tackle difficult problems without feeling overwhelmed, while ensuring that simpler tasks are completed efficiently. This balance is crucial for achieving the best results.
Steps to Plan Your Time Effectively
Here are some strategies to help manage your time efficiently during any assessment:
- Read Instructions Carefully: Begin by reviewing the entire set of questions to understand what is required before diving into solving them.
- Divide Your Time: Allocate specific time slots to different sections or question types to ensure that no part is neglected.
- Start with What You Know: Tackle the easier problems first to build momentum and gain confidence.
Practical Tips for Staying on Track
To maintain focus and ensure you don’t run out of time, consider these practical approaches:
- Keep an Eye on the Clock: Regularly check the time to ensure you’re staying on pace and adjust if necessary.
- Don’t Get Stuck: If you find yourself spending too much time on a difficult problem, move on and return to it later with a fresh perspective.
- Leave Time for Review: Make sure to leave the last few minutes to review your work and check for any possible mistakes.
By implementing these strategies, you can approach any assessment with a structured mindset, giving you the best chance to perform well under pressure.
When to Seek Additional Help
Sometimes, despite your best efforts, certain concepts or problems remain unclear. Recognizing when it’s time to seek extra assistance can make a significant difference in understanding challenging material. It’s important to know that asking for help is not a sign of weakness, but rather a proactive approach to mastering difficult subjects.
When you feel stuck or unable to solve specific problems, reaching out for guidance ensures that you continue to make progress. The sooner you address any confusion, the less likely it is to snowball into larger gaps in understanding.
Signs You Should Seek Help
Here are a few indicators that it may be time to ask for assistance:
| Indicator | Suggested Action |
|---|---|
| Unable to Understand Core Concepts | Seek a tutor or attend a study session to clarify foundational ideas. |
| Consistently Making the Same Mistakes | Work with a teacher or mentor to identify where you’re going wrong and correct your approach. |
| Running Out of Time for Independent Study | Join group study sessions or get focused help to cover topics more efficiently. |
| Feeling Overwhelmed or Anxious | Talk to a counselor or educator for emotional support and to manage stress. |
Where to Find Additional Help
There are several resources available to get the extra support you need:
- Teachers: Often the best resource for understanding concepts and clearing up confusion.
- Tutors: Professional tutors can provide one-on-one guidance tailored to your needs.
- Study Groups: Collaborating with classmates can help explain difficult topics in different ways.
- Online Forums and Resources: Websites and apps often provide explanations, practice problems, and step-by-step solutions.
Don’t hesitate to reach out for help when needed; it’s a crucial step towards mastering any subject effectively.
Real-World Applications of Mathematical Skills
The ability to solve equations and manipulate variables extends far beyond the classroom. The concepts learned in math can be applied to a variety of real-world scenarios, from managing personal finances to solving complex engineering problems. Understanding how mathematical thinking works in everyday life can not only enhance problem-solving abilities but also open doors to numerous career opportunities.
Whether you’re designing a building, managing a budget, or making business decisions, the skills you develop in this area play an essential role in many professions and personal tasks. Here are a few examples of how these skills are used practically:
Common Uses in Various Fields
- Finance: Understanding percentages, ratios, and proportional relationships is crucial for budgeting, calculating interest rates, and managing investments.
- Engineering: Engineers use mathematical models and equations to design structures, analyze materials, and optimize systems.
- Technology: Programmers rely on algorithms and mathematical logic to develop software and solve problems within coding challenges.
- Medicine: Doctors and researchers use statistical methods to analyze data, calculate dosages, and understand trends in healthcare.
- Economics: Economists use complex mathematical models to predict market behavior and make decisions based on data trends.
Everyday Life Applications
- Shopping: Comparing prices, calculating discounts, and determining the best deals all require a basic understanding of numbers and percentages.
- Cooking: Adjusting recipes based on serving sizes involves working with proportions and measurements.
- Home Improvement: Whether you’re laying tile or measuring for furniture, understanding measurements and spatial relationships is essential.
By recognizing the broad scope of applications for these skills, it’s easier to see the importance of mastering them. They empower individuals to navigate a wide range of situations and make informed decisions, both professionally and personally.
How to Stay Calm During the Test
Managing stress and staying calm during a high-pressure situation is crucial for performing well. When faced with a challenging assessment, it’s easy to feel overwhelmed, but maintaining composure can greatly improve your ability to focus and solve problems efficiently. Here are some strategies to help you stay relaxed and confident throughout the process.
Preparation Before the Test
Being well-prepared is the first step to staying calm. When you have reviewed the material thoroughly and practiced different problem-solving techniques, you’ll be more confident in your abilities. Here are some helpful steps to take in the days leading up to the test:
- Review key concepts: Go over important topics and practice problems to reinforce your knowledge.
- Practice under timed conditions: Simulate test conditions to get used to the time constraints.
- Get plenty of rest: Ensure you have adequate sleep the night before, as fatigue can affect concentration.
- Eat a balanced meal: Fuel your body with nutritious foods that will help maintain energy and focus.
During the Test
Once you’re in the testing environment, it’s important to remain calm and focused. Here are some strategies you can use to manage stress while taking the test:
- Take deep breaths: If you feel anxious, pause for a moment and breathe deeply to calm your mind.
- Focus on one question at a time: Avoid worrying about the questions you haven’t reached yet. Concentrate on the current problem.
- Keep a positive mindset: If you encounter a tough question, remind yourself that you can handle it. Stay confident.
- Time management: Use your time wisely, but don’t rush. If you get stuck on a question, move on and return to it later if possible.
Key Tips for Remaining Calm
| Tip | Benefit |
|---|---|
| Stay organized: | Helps you feel in control and reduces unnecessary stress. |
| Positive self-talk: | Boosts confidence and reduces negative thinking. |
| Stay hydrated: | Maintains focus and prevents distractions due to dehydration. |
By implementing these strategies, you can create an environment where you feel more in control and confident, which will enable you to approach each question with a clear, focused mindset.
Building a Strong Foundation for Math Success
Establishing a solid base in mathematical concepts is essential for tackling more advanced topics. When the fundamentals are well understood, it becomes easier to grasp complex ideas and solve challenging problems. A strong foundation involves mastering basic skills, developing problem-solving techniques, and reinforcing key strategies that support deeper learning.
To build this foundation, focus on practicing basic operations, recognizing patterns, and becoming comfortable with different types of equations. By approaching each new concept methodically and practicing regularly, you’ll develop the confidence and skill needed to succeed in higher-level tasks.
Here are some key strategies to help strengthen your grasp on essential mathematical principles:
- Master the basics: Start by understanding simple operations and their properties. This will make advanced concepts more intuitive.
- Practice regularly: Consistency is key. Set aside time each day or week to work on problems and review concepts.
- Use various resources: Different learning materials, such as textbooks, online tutorials, and practice sheets, can offer varied explanations and examples.
- Ask questions: Don’t hesitate to seek clarification when you’re unsure. Understanding small details can prevent bigger issues later.
- Apply what you learn: Practice applying concepts to real-world scenarios to improve your problem-solving skills.
Building a strong base in math requires patience and persistence. Focus on mastering each step, and over time, you’ll find that more complex ideas will feel less daunting. With a solid foundation, you’ll be well-equipped to face future challenges with confidence.
Using the Solution Guide to Track Progress
Utilizing a solution guide is a great way to monitor your development and pinpoint areas that need improvement. By comparing your results with the provided solutions, you can identify patterns in your mistakes and track your understanding over time. This process allows you to not only check for correctness but also to reflect on the methods used to reach a solution, which aids in building a deeper understanding of the material.
Regularly checking your work with the guide helps in several ways:
- Recognizing mistakes: Spotting errors early allows you to address them before they become habits.
- Identifying weak spots: Repeated errors in similar types of problems highlight areas where additional practice or review is necessary.
- Improving problem-solving skills: Analyzing the solutions can help you discover new techniques or strategies for solving similar problems more efficiently.
- Tracking improvement: By consistently comparing your solutions to the guide, you can visually track your progress and see how much you’ve learned.
By actively using a solution guide as a tool, you turn each problem into a learning opportunity. This process not only reinforces your current understanding but also boosts confidence as you notice your skills improving over time. The more you engage with the material in this way, the more prepared you’ll be for future challenges.