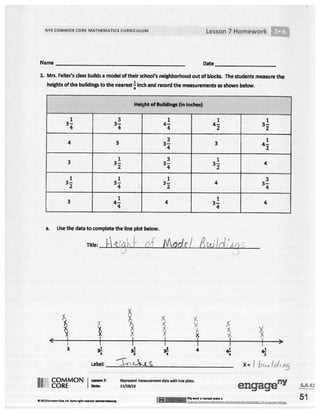
Here is a plan for an informational article on the topic “Eureka Math Grade 5 Lesson 7 Homework Answer Key” with 15 unique headings: Understanding Eureka Math Grade 5
This article provides a comprehensive overview of a specific educational resource designed to support students in mastering key mathematical concepts. It breaks down the structure, highlights important topics covered, and offers guidance for parents and educators to assist in the learning process. With a focus on clarity, the resource aims to strengthen foundational knowledge through various methods of instruction and practice.
Introduction to the Learning Resource
Discover how the materials are structured to enhance understanding, providing students with both practice exercises and detailed explanations for solving problems effectively.
Core Topics Covered in the Curriculum

- Introduction to key principles and foundational ideas.
- Step-by-step breakdown of complex concepts for easier comprehension.
- Practice exercises designed to reinforce core knowledge.
Purpose and Goals of the Program
- Equip students with essential problem-solving skills.
- Encourage critical thinking and logical reasoning.
- Support both individual and collaborative learning environments.
How to Navigate the Resource
Learn how to effectively use the provided guide to support your child’s learning journey. The resource is designed to be user-friendly, with clear directions for both teachers and learners.
Support for Students
Discover how exercises are tailored to cater to various learning speeds, allowing students to build confidence as they progress.
Incorporating Practice Exercises
- Engage with a variety of questions that enhance understanding.
- Reinforce concepts through regular, incremental practice.
Assessing Student Progress
Evaluation methods are integrated to track students’ progress, offering insights into areas needing further focus.
Working with Parents and Educators
- Collaborative efforts between educators and parents can further boost student performance.
- Provide tips for helping children at home.
Expanding Problem-Solving Skills
Exercises are designed to promote logical thinking, helping students tackle a variety of challenges both in and out of the classroom.
Visual Learning Aids
- Illustrations and diagrams complement written explanations to improve understanding.
- Visual tools are an integral part of the learning process, helping students visualize abstract concepts.
Interactive Activities
Dynamic activities are included to keep students engaged, providing hands-on experience with the material.
Building Conceptual Connections
The program helps students connect different mathematical principles, fostering a deeper understanding of how concepts relate to one another.
Overcoming Common Challenges
- Addressing areas where students typically struggle, with additional resources for remediation.
- Providing strategies for overcoming confusion in complex topics.
Feedback and Improvement
Continuous feedback loops are established, allowing students to identify areas for improvement and track their development over time.
Conclusion and Further Resources
Summarizing key takeaways and providing further resources for those interested in exploring the subject matter in more depth.
Mastering Fifth Grade Math Techniques
Developing proficiency in numerical skills at this stage is crucial for building a strong foundation. Students are introduced to a variety of strategies designed to enhance their problem-solving abilities and boost their confidence. By focusing on key concepts and practicing regularly, learners can easily grasp the essential principles required for future success.
Understanding Core Concepts
At this level, it’s important to focus on core strategies that simplify complex ideas. These techniques enable students to break down challenging tasks into smaller, more manageable steps. Emphasizing logical reasoning and critical thinking helps improve both accuracy and efficiency, allowing students to approach problems with confidence.
Building Strong Calculation Habits
Regular practice plays a significant role in solidifying calculation skills. Encouraging a structured approach to exercises helps students recognize patterns and apply learned techniques more effectively. By mastering basic operations and gradually advancing to more complex problems, students can strengthen their overall proficiency and gain a deeper understanding of mathematical processes.
Breaking Down Complex Problems
When faced with intricate tasks, the best approach is to decompose them into smaller, more manageable parts. This strategy helps to reduce overwhelm and allows for clearer focus on each step. By simplifying challenges and tackling one piece at a time, individuals can make steady progress toward finding solutions, even in the most complicated situations.
One effective method is to first identify the core elements of the problem. Understanding what is being asked and determining the key components allows for a structured approach. Breaking the task into logical sequences of actions ensures that no critical detail is overlooked, leading to more precise and accurate outcomes.
Tips for Finding the Right Approach
Choosing the most effective method to tackle a challenge requires careful consideration and planning. Rather than jumping straight into a problem, it’s helpful to explore different strategies and evaluate which one aligns best with the task at hand. A thoughtful approach ensures that efforts are focused and resources are used efficiently, leading to a more successful outcome.
Identify the Key Elements
Before deciding on a course of action, it’s essential to break down the task and identify its fundamental components. Recognizing the core aspects helps streamline the problem-solving process and ensures that no crucial detail is overlooked. Here are some tips to get started:
- Clarify the objective and desired outcome.
- Break the problem into smaller, easier-to-handle sections.
- Identify any patterns or similarities with previous problems.
Choose the Best Method
Once the key elements are understood, select a strategy that suits the problem’s nature. Consider these steps when choosing the best approach:
- Assess the tools and resources you have available.
- Evaluate different methods based on their effectiveness and efficiency.
- Test your chosen approach on smaller, related tasks before applying it to the main problem.
How to Check Your Answers
Verifying your results is an essential step in ensuring accuracy and confidence in your work. It involves reviewing the process and outcomes to confirm that the steps were followed correctly. By checking your results carefully, you can identify any mistakes and make adjustments before finalizing your solution.
Review the Steps Taken
Start by retracing your steps to ensure that each action was completed correctly. Compare each stage of the process with the instructions or guidelines to see if any part was overlooked or misunderstood. This step helps catch small errors and reinforces the correct approach.
Use Alternative Methods for Verification
If possible, apply a different technique or strategy to check the outcome. This could involve using estimation, reverse calculations, or a different formula to confirm the validity of your results. By cross-checking with multiple methods, you can further verify that your solution is reliable.
Verification Methods for Accuracy
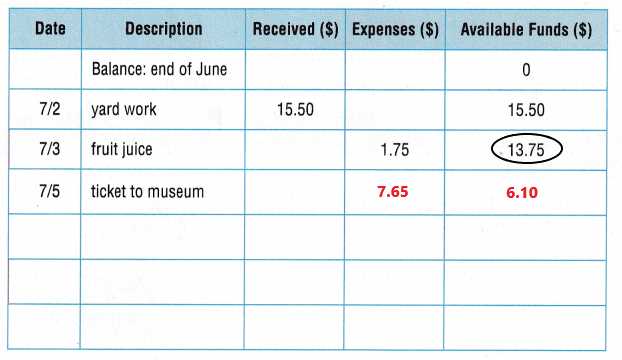
Ensuring the correctness of your results is a critical aspect of any problem-solving process. By using various verification methods, you can confirm that the outcomes align with expectations. These techniques provide a reliable way to detect errors and confirm that the solution is accurate before concluding the task.
Cross-Check with Alternative Techniques
One effective verification method is to apply a different technique or approach to solve the same problem. This can reveal inconsistencies or confirm that the initial result was obtained correctly. For instance, using a different formula or method can offer a fresh perspective and strengthen the overall confidence in the outcome.
Use Estimation and Approximation
Another useful approach is to estimate the answer before performing the detailed calculations. Estimating helps set a benchmark for the expected result. After completing the full solution, compare it with your estimate to check for any significant discrepancies. If the answer is far from the estimate, it could indicate a mistake that needs correction.
Using Visual Aids for Better Understanding
Visual tools can significantly enhance comprehension, making complex concepts easier to grasp. By representing information in a visual format, learners can better visualize relationships, patterns, and processes. Diagrams, charts, and graphs simplify abstract ideas and allow for quicker insight, promoting a deeper understanding of the material.
One common technique is using diagrams to illustrate problems step-by-step. These visual representations break down the information, helping to clarify the process and showing how each element connects to the next. Charts and graphs also provide a clearer way to interpret data, offering an immediate understanding of trends or comparisons.
Illustrating Problems Effectively
Visual representation of problems can greatly enhance understanding and simplify complex tasks. By transforming abstract ideas into clear, visual forms, individuals can better follow the logical steps required to find a solution. Illustrations, such as diagrams or charts, not only clarify the process but also provide a structured way to analyze and solve challenges.
Using Diagrams and Charts
Diagrams and charts can serve as powerful tools for illustrating problems. They help break down tasks into smaller, digestible components, making it easier to follow the steps needed to reach a solution. By using visuals, learners can see how elements relate to one another and gain a clearer understanding of the problem at hand.
Example Table for Problem Breakdown
Here’s an example of how a table can be used to break down a problem and illustrate its components:
| Step | Description | Visual Aid |
|---|---|---|
| 1 | Identify the key elements of the problem | Diagram showing components |
| 2 | Break down the task into smaller steps | Flowchart illustrating process |
| 3 | Use a table to organize the information | Example table for organization |
Why Lesson 7 is Critical
This stage is crucial in building foundational skills that will support future learning. It introduces key concepts that connect to more advanced topics, making it an essential part of the learning journey. By mastering these principles, learners can develop a deeper understanding and prepare themselves for more complex challenges ahead.
Building Strong Foundations
The concepts covered in this section are foundational. Understanding them is key to unlocking further progress in more challenging areas. This part of the curriculum is designed to bridge gaps, ensuring that learners are well-prepared to handle more intricate problems in the future.
Key Concepts Introduced
Here’s a breakdown of the essential components covered in this stage:
| Concept | Description | Importance |
|---|---|---|
| Core Principles | Understanding basic concepts that are crucial for future learning. | Provides a foundation for more complex topics. |
| Problem-Solving Techniques | Introducing methods to tackle problems systematically. | Encourages structured thinking and accuracy. |
| Application of Strategies | Learning how to apply strategies to different scenarios. | Enhances adaptability in solving various types of problems. |
Building a Strong Foundation
Establishing a solid base of essential concepts is crucial for success in more advanced topics. By focusing on the core principles, learners can develop a deep understanding that will support their progress in solving increasingly complex problems. A strong foundation not only improves confidence but also ensures that each step in the learning process is built on a reliable understanding.
Key Areas of Focus
To build a strong foundation, it is essential to concentrate on a few key areas:
- Core Concepts: Understanding fundamental principles that are applicable in various contexts.
- Problem-Solving Skills: Developing strategies to approach challenges systematically and logically.
- Confidence in Application: Practicing the use of these skills in real-life scenarios to reinforce learning.
Steps for Strengthening Fundamentals
Here are some effective steps to strengthen the foundational knowledge:
- Review basic principles regularly to ensure a solid grasp of the concepts.
- Practice applying strategies through exercises and real-world examples.
- Seek clarification on any areas of confusion to prevent gaps in understanding.
Linking Concepts to Real Life
Connecting classroom concepts to real-world applications helps students see the practical value of what they are learning. By demonstrating how abstract ideas are used in everyday situations, learners can understand the relevance of their studies. This approach not only makes learning more engaging but also encourages problem-solving skills that are applicable beyond the classroom.
Real-life examples can range from budgeting and shopping to designing structures and analyzing data. These scenarios highlight how theoretical knowledge can be applied to solve practical problems, reinforcing the importance of foundational learning. By making these connections, students gain a deeper appreciation for their studies and are better prepared to tackle challenges in the future.
Applications of Fifth Grade Skills
The skills learned in the fifth year of learning provide a solid foundation for real-world problem-solving. These abilities are not only crucial for academic success but are also directly applicable to various everyday tasks. By mastering these concepts, students can tackle real-life situations with confidence and develop critical thinking skills that will benefit them in many aspects of life.
From calculating distances to planning budgets, the skills acquired in this stage have numerous applications. These principles enable students to approach practical challenges more effectively and prepare them for more advanced problem-solving tasks in the future. Whether it’s managing time, understanding measurements, or analyzing data, the knowledge gained during this period forms a key part of everyday decision-making.