Geometry Chapter 7 Answers and Solutions

In this section, we delve into the essential principles and techniques used to solve complex problems in the study of shapes, angles, and measurements. Whether you are looking to sharpen your skills or clarify challenging concepts, understanding the core methods is crucial for mastering this area of study.

Step-by-step solutions break down the problems, offering clear paths to the correct outcomes. From basic properties to advanced applications, these explanations aim to simplify even the most intricate topics.

Practical tips are provided to help you improve your problem-solving approach and avoid common pitfalls. By following these strategies, you can enhance both your comprehension and performance in this field.

Solutions and Explanations for Key Concepts

This section offers detailed explanations and step-by-step solutions to the problems presented in this part of the course. The focus is on helping you understand the underlying principles and how to apply them effectively to various questions.

To achieve a deeper understanding, we break down each problem into smaller, more manageable steps. This approach allows you to follow the logic behind each solution and see how different concepts are interconnected.

• Step-by-step breakdowns: Each problem is broken down into smaller steps to ensure clarity and make the process easier to follow.
• Practical applications: Real-world examples show how these concepts can be applied outside of textbooks, making the material more relatable.
• Common pitfalls: We highlight frequent mistakes and explain how to avoid them, improving accuracy in solving similar problems.

By reviewing the solutions carefully and practicing the outlined methods, you’ll be well-equipped to tackle even the more challenging problems that may arise in this area of study.

Key Concepts in Geometry Chapter 7

This section covers the foundational ideas and important techniques that will guide you through the various problems and concepts in this part of the subject. Mastering these concepts is crucial for solving more complex challenges effectively.

Fundamental Principles

• Angle Relationships: Understanding how angles interact in different configurations, including complementary, supplementary, and vertical angles, is essential for solving many types of problems.
• Congruence: Recognizing when two shapes are congruent allows you to apply specific rules to solve problems involving matching figures.
• Parallel Lines: Identifying properties of parallel lines and transversal intersections helps in determining angle measures and solving geometric proofs.

Advanced Applications

• Triangles: Understanding various types of triangles and their properties, such as congruency and similarity, allows for solving complex problems involving sides and angles.
• Theorems: Key theorems, such as the Pythagorean Theorem, are instrumental in solving problems related to right triangles and distances.
• Coordinate Geometry: Using the coordinate plane to solve problems involving distance, midpoints, and slopes brings a practical aspect to theoretical concepts.

Understanding Geometric Proofs Step by Step

In this section, we will explore the process of constructing logical arguments to prove certain statements about shapes and their properties. A geometric proof involves a series of clear steps, each building on the previous one, to show the truth of a given statement.

Breaking Down the Structure

Every proof follows a structured format, starting with known facts and working towards a conclusion. The typical elements of a proof include:

• Given Information: These are the facts or assumptions provided in the problem statement.
• To Prove: The goal or the statement that needs to be demonstrated.
• Proof Steps: Logical deductions made from the given information and previous steps, leading to the desired conclusion.

Approach and Techniques

• Direct Proof: Involves a straightforward sequence of logical steps based on definitions, postulates, and previously proven theorems.
• Indirect Proof: Also known as proof by contradiction, where you assume the opposite of what you’re trying to prove and show that it leads to a contradiction.

By following these systematic steps and applying the appropriate reasoning methods, anyone can learn to create rigorous proofs that demonstrate geometric relationships accurately and logically.

Important Theorems to Know

In this section, we focus on the key principles and theorems that serve as the foundation for solving a wide range of problems. Mastering these theorems will allow you to tackle complex questions with confidence and clarity.

Essential Theorems

There are several fundamental theorems that are widely applied in various problems. Understanding their proofs and applications is crucial for progressing in this field.

Theorem	Description	Application
Pythagorean Theorem	Describes the relationship between the sides of a right triangle.	Used to find the length of a side in a right triangle when the other two sides are known.
Angle Sum Theorem	The sum of the angles in any triangle is always 180 degrees.	Helps in finding missing angles in triangles.
Parallel Postulate	If two lines are cut by a transversal and the alternate interior angles are congruent, the lines are parallel.	Used to prove lines are parallel based on angle relationships.
Congruence Theorems (SSS, SAS, ASA)	Conditions under which two triangles are congruent.	Used to prove that two triangles are congruent based on specific side and angle relationships.

Advanced Theorems

In addition to the fundamental theorems, there are more advanced principles that are essential for tackling complex geometric problems. These theorems often require deeper understanding and more detailed reasoning.

Theorem	Description	Application
Euclid’s Theorem	Describes the uniqueness of parallel lines through a given point.	Helps in understanding the properties of parallel lines and their behavior in different configurations.
Intercept Theorem	States that if a transversal intersects two parallel lines, the segments of the transversal are proportional.	Useful for solving problems involving proportional relationships in geometric figures.

Familiarity with these theorems will not only help you solve problems efficiently but also strengthen your overall understanding of the subject.

How to Solve Word Problems in Mathematics

Word problems in mathematics often present real-world scenarios where you must apply concepts and formulas to find a solution. The key to solving these problems lies in understanding the relationships between the given information and the unknowns you’re asked to solve for.

Step-by-Step Approach

To solve a word problem effectively, follow these steps:

1. Read the Problem Carefully: Take time to fully understand the situation. Identify the key facts and figures provided.
2. Identify What You Need to Find: Focus on the question or goal of the problem. What is being asked?
3. Draw a Diagram (if applicable): Visualizing the problem can often make it easier to understand the relationships between different elements.
4. Translate Words into Equations: Convert the described relationships and facts into mathematical expressions or equations.
5. Apply the Relevant Theorems and Formulas: Use the appropriate principles and formulas to solve for the unknowns.
6. Check Your Work: After calculating, review your solution to ensure it makes sense in the context of the problem.

Common Strategies

• Using Proportions: Many word problems involve ratios or proportions. Setting up and solving these can help you find unknown values.
• Applying Algebraic Methods: Word problems often require setting up and solving equations, which is where algebra comes into play.
• Utilizing Geometric Properties: When dealing with shapes, properties such as area, perimeter, and angle relationships are essential tools.

By following these steps and strategies, you’ll be better equipped to tackle word problems and approach them with confidence.

Step-by-Step Guide for Triangle Congruence

Understanding how to determine if two triangles are congruent is a crucial skill in this field of study. When two triangles are congruent, their corresponding sides and angles are equal, which allows for various geometric proofs and problem-solving techniques. In this section, we will guide you through the process of checking triangle congruence using key criteria.

To prove that two triangles are congruent, there are several methods available, each based on different combinations of sides and angles. These methods are the foundation for proving the equality of two figures.

Congruence Criteria

• Side-Side-Side (SSS): If all three sides of one triangle are equal to the corresponding sides of another triangle, the triangles are congruent.
• Side-Angle-Side (SAS): If two sides and the included angle of one triangle are equal to the corresponding parts of another triangle, the triangles are congruent.
• Angle-Side-Angle (ASA): If two angles and the included side of one triangle are equal to the corresponding parts of another triangle, the triangles are congruent.
• Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are equal to the corresponding parts of another triangle, the triangles are congruent.

Steps for Verifying Congruence

• Identify Corresponding Parts: Look at the given information and determine which sides and angles of the two triangles are being compared.
• Apply the Congruence Criteria: Based on the information provided, choose the appropriate method (SSS, SAS, ASA, AAS) to check for congruence.
• Check the Result: If the triangles meet the criteria, they are congruent. If not, further analysis may be required.

By following these steps and using the congruence criteria, you will be able to confidently determine whether two triangles are congruent and apply this knowledge in various geometric proofs and problems.

Properties of Parallel Lines Explained

Parallel lines are fundamental in understanding various geometric concepts. They are defined by their consistent direction and equal distance between each other, no matter how far they are extended. Recognizing the properties and relationships that exist when parallel lines are intersected by other lines can help solve a wide range of problems in mathematics.

One of the most important properties of parallel lines is the way they interact with transversals–lines that intersect them at an angle. These interactions lead to specific relationships between angles, which are key to solving many geometric problems.

Key Properties of Parallel Lines

Property	Description	Example
Corresponding Angles	If a transversal crosses two parallel lines, each pair of corresponding angles is congruent.	When two parallel lines are intersected by a transversal, angle 1 equals angle 2.
Alternate Interior Angles	Alternate interior angles are congruent when two parallel lines are cut by a transversal.	If two parallel lines are intersected by a transversal, angle 3 equals angle 4.
Alternate Exterior Angles	Alternate exterior angles are congruent when two parallel lines are intersected by a transversal.	If two parallel lines are intersected by a transversal, angle 5 equals angle 6.
Consecutive Interior Angles	Consecutive interior angles are supplementary when two parallel lines are intersected by a transversal.	Angle 7 + angle 8 = 180° when the lines are parallel.

These properties are essential for solving problems involving parallel lines and transversals. Understanding how angles relate to one another when parallel lines are involved will greatly enhance your ability to approach and solve complex geometric problems.

Applications of Pythagorean Theorem

The Pythagorean Theorem is a fundamental principle in mathematics that establishes a relationship between the sides of a right triangle. This theorem is not only crucial for solving geometric problems but also has practical applications in various fields. By using this theorem, we can calculate distances, analyze shapes, and solve problems involving right-angled figures.

In real-life situations, the Pythagorean Theorem is applied in areas such as architecture, navigation, physics, and engineering. It helps to determine unknown distances when two sides of a right triangle are known, making it a valuable tool for problem-solving in many contexts.

Everyday Uses of the Pythagorean Theorem

The Pythagorean Theorem can be used in everyday life to calculate distances and measurements in a wide range of situations:

• Building and Construction: In construction, the theorem helps ensure that corners are square by confirming that the sides of a right triangle are proportional.
• Navigation: Pilots and sailors use the theorem to determine the shortest route between two points, especially when traveling along diagonal paths.
• Designing and Carpentry: When laying out designs, builders often use the theorem to measure and verify right angles and distances between points.

Applications in Science and Engineering

In scientific fields, the Pythagorean Theorem plays an essential role in calculations involving space and motion:

• Physics: The theorem is used to determine the resultant vector in motion problems, where two components of motion are at right angles to each other.
• Engineering: Engineers apply the theorem in structural analysis, robotics, and various design projects where accurate measurement of distances is required.

By using this simple but powerful tool, professionals across many industries are able to solve complex problems with ease and accuracy.

Exploring Coordinate Geometry Techniques

Coordinate geometry provides a powerful framework for solving geometric problems using algebraic methods. By assigning coordinates to points on a plane, we can apply algebraic equations to find distances, midpoints, slopes, and more. This technique bridges the gap between algebra and geometry, allowing for a more precise and systematic approach to solving problems involving shapes and lines.

One of the most important aspects of coordinate geometry is the ability to analyze relationships between geometric figures using their coordinates. By working with equations, slopes, and intercepts, we can easily determine properties of lines, circles, and other shapes in a coordinate plane.

Key Techniques in Coordinate Geometry

There are several techniques in coordinate geometry that are essential for solving problems involving points, lines, and other geometric figures:

• Distance Formula: The distance between two points in a plane can be calculated using the distance formula, which is derived from the Pythagorean theorem. This formula is particularly useful for finding the length of segments and determining if two points are equidistant from a given point.
• Slope Formula: The slope of a line is determined by the ratio of the change in y-coordinates to the change in x-coordinates. This helps to understand the direction of a line and is essential for determining if two lines are parallel or perpendicular.
• Midpoint Formula: The midpoint of a segment is the point that divides it into two equal parts. Using the midpoint formula, we can calculate this point by averaging the x and y coordinates of the endpoints.

Applications in Problem Solving

Coordinate geometry is widely used in solving various geometric problems, especially when dealing with figures placed on a coordinate plane. Some common applications include:

• Finding Equation of a Line: Given the slope and a point on the line, we can use the point-slope form to find the equation of a line. This is fundamental for determining relationships between different geometric objects.
• Identifying Properties of Figures: By applying coordinate geometry techniques, we can identify properties of polygons, such as whether a quadrilateral is a rectangle or a rhombus, based on the slopes and distances between its vertices.

By mastering these techniques, students and professionals alike can solve complex geometric problems with greater ease and accuracy.

Methods for Solving Angle Problems

Angles play a crucial role in various geometric problems, and understanding how to solve them is essential for problem-solving. By applying specific techniques and formulas, one can easily calculate missing angles in polygons, intersecting lines, or various geometric figures. Different types of angle relationships, such as complementary, supplementary, and vertical angles, provide a systematic way to approach these problems.

Solving angle problems often involves using known properties and theorems to find unknown values. These techniques not only help simplify the process but also ensure accuracy in calculations. Whether dealing with parallel lines, triangles, or other shapes, understanding how angles relate to one another is key to reaching the correct solution.

Key Techniques for Angle Calculation

Several methods are commonly used when solving angle problems:

• Using Angle Sum Property: In polygons, the sum of interior angles can be found using the formula: (n – 2) × 180°, where “n” is the number of sides. This is particularly useful for determining angles in triangles, quadrilaterals, and other polygons.
• Complementary and Supplementary Angles: Complementary angles add up to 90°, while supplementary angles sum to 180°. These relationships are often used in problems involving pairs of angles formed by parallel lines and transversals.
• Vertical Angles: When two lines intersect, the opposite angles (vertical angles) are congruent. This property is useful when dealing with intersecting lines and can help quickly solve for unknown angles.

Applications in Different Figures

Angle-solving techniques are applied across different geometric figures. Here are some common examples:

• Triangles: The sum of the interior angles of any triangle is always 180°. This fundamental property can help solve for unknown angles when at least two angles are known.
• Parallel Lines: When a transversal cuts through parallel lines, various angle relationships such as corresponding angles, alternate interior angles, and consecutive interior angles are established, which can be used to find unknown angles.
• Quadrilaterals: In quadrilaterals, the sum of the interior angles is always 360°. This can be applied to find missing angles when dealing with parallelograms, rectangles, or trapezoids.

By applying these methods, solving angle problems becomes more straightforward, allowing for quick and accurate results in a variety of geometric scenarios.

Real-World Geometry Problem Solving

In everyday life, we encounter a variety of situations that require solving problems related to shapes, spaces, and measurements. Whether it’s designing a building, planning a garden, or determining the size of a piece of furniture, applying spatial reasoning and mathematical principles allows us to make accurate decisions and achieve practical solutions. Real-world problem solving often involves translating complex visual scenarios into manageable calculations, making it essential to understand how mathematical concepts work in a practical context.

By using mathematical tools and techniques, such as measuring angles, calculating areas, and understanding relationships between different geometric shapes, we can solve problems that arise in many fields, from architecture and engineering to art and nature. This approach not only simplifies problem solving but also helps us make more informed decisions when faced with practical challenges.

Practical Applications in Architecture and Design

In architecture and design, geometric principles are fundamental to creating functional and aesthetically pleasing structures. Some common real-world problems include:

• Designing Floor Plans: Architects use geometry to design floor plans by calculating the areas of rooms, ensuring that space is used efficiently. Understanding the relationships between different shapes allows for the creation of well-balanced and practical layouts.
• Estimating Materials: When building structures or creating art, determining the amount of materials needed–such as tiles, paint, or fabric–requires precise calculations based on area, volume, and surface measurements.

Solving Problems in Nature and Environment

Geometry is also deeply embedded in nature and environmental planning. Some examples include:

• Landscaping and Garden Design: When planning a garden, understanding the proportions of shapes and how to efficiently use space is crucial. This involves calculating the area of flowerbeds, walkways, and patios, as well as considering how different shapes interact.
• Mapping and Navigation: Surveying land for construction projects or determining the shortest route between two points on a map involves using geometric methods, such as measuring distances and angles.

By applying geometric principles to real-world problems, we can find solutions that are both practical and efficient, ultimately leading to better outcomes in design, construction, and everyday decision-making.

How to Use Trigonometric Ratios

Trigonometric ratios are powerful tools used to solve problems involving right-angled triangles. These ratios establish a relationship between the angles and sides of a triangle, allowing for the calculation of unknown sides or angles when certain values are known. By applying the basic trigonometric functions, one can simplify complex problems, especially in fields like engineering, physics, and navigation.

In this section, we will explore how to effectively use the three primary trigonometric ratios–sine, cosine, and tangent–and apply them to real-world scenarios. Understanding these ratios and their applications helps make solving triangle-related problems more systematic and manageable.

Basic Trigonometric Ratios

Trigonometric ratios are based on the relationships between the angles and sides of a right triangle. The three main functions are:

• Sine (sin): The sine of an angle is the ratio of the length of the opposite side to the hypotenuse. It is written as: sin(θ) = opposite/hypotenuse.
• Cosine (cos): The cosine of an angle is the ratio of the length of the adjacent side to the hypotenuse. It is written as: cos(θ) = adjacent/hypotenuse.
• Tangent (tan): The tangent of an angle is the ratio of the length of the opposite side to the adjacent side. It is written as: tan(θ) = opposite/adjacent.

Applications of Trigonometric Ratios

Trigonometric ratios are used in a variety of fields, especially when dealing with distances, angles, and elevations. Here are a few common applications:

• Finding Unknown Sides: When you know one side and one angle of a right triangle, you can use trigonometric ratios to find the other sides. For example, if you know the angle and the length of the hypotenuse, you can use the sine or cosine function to find the opposite or adjacent side.
• Solving for Angles: When the sides of a triangle are known, trigonometric ratios can help calculate the angles. By rearranging the trigonometric equations and using the inverse functions (sin⁻¹, cos⁻¹, tan⁻¹), you can determine the measure of an unknown angle.
• Applications in Real-World Problems: Trigonometry is commonly used in fields such as architecture, astronomy, and navigation. For example, when calculating the height of a building using a known distance from the building and the angle of elevation, trigonometric ratios provide a straightforward method for finding the unknown height.

Mastering trigonometric ratios is essential for solving a wide range of practical problems involving triangles. By understanding how to apply sine, cosine, and tangent, you can tackle problems more efficiently and accurately.

Tips for Test Preparation

Effective preparation for any exam requires a structured approach, particularly when dealing with subjects that involve logical reasoning and problem-solving. The key to performing well lies in understanding the core concepts, practicing consistently, and applying strategies that make the learning process more efficient. By focusing on the most relevant topics and honing specific skills, you can approach your exam with confidence.

In this section, we will explore several helpful tips that will guide you through the process of studying for tests focused on problem-solving and reasoning. Whether you’re reviewing geometric concepts, mathematical principles, or spatial relationships, these strategies will help you tackle even the most challenging problems with ease.

Focus on Key Concepts

Before diving into practice problems, it’s important to identify and fully understand the main concepts and theorems that frequently appear on exams. Reviewing your class notes, textbooks, or online resources will provide insight into the most important topics. Key areas to focus on include:

• Formulas and Theorems: Memorize essential formulas such as those for areas, volumes, and the relationships between different shapes. This will help you solve problems more quickly during the test.
• Problem-Solving Strategies: Learn common techniques for solving problems, such as breaking down complex questions into smaller, manageable parts, and applying logical reasoning to find solutions.
• Visualization: Being able to visualize shapes and their properties can significantly improve your understanding of the material. Use diagrams and sketches to help clarify concepts and facilitate problem-solving.

Practice Regularly and Review Mistakes

Practice is essential to reinforcing the concepts you learn. Regularly solving a variety of practice problems, including those from past exams, will help you identify patterns and understand how questions are typically structured. It also builds your speed and accuracy in solving problems under timed conditions. Additionally, it’s important to:

• Analyze Mistakes: After completing practice problems, take the time to review your errors. Understanding why you made a mistake will help you avoid it in the future and improve your overall performance.
• Use Online Resources: There are many online tools and platforms that offer practice problems, quizzes, and video explanations. These resources can complement your studies and provide additional perspectives on the material.
• Study in Groups: Collaborative learning can be a helpful way to solidify concepts. Working with peers allows you to share knowledge and solve problems together, providing a more comprehensive understanding of the material.

By focusing on these strategies and committing to consistent practice, you’ll be better prepared for your test and able to approach problems with clarity and confidence.

Common Mistakes and How to Avoid Them

In the process of solving mathematical problems, certain errors tend to be more frequent, especially when dealing with logical reasoning and spatial relationships. Understanding and recognizing these common mistakes can significantly improve your ability to solve problems correctly and efficiently. By being aware of these pitfalls and learning strategies to avoid them, you can approach each task with greater confidence and accuracy.

In this section, we will explore some of the most common mistakes that occur during problem-solving and provide useful tips on how to avoid them. Whether it’s a simple miscalculation or a more complex misunderstanding of a concept, knowing where mistakes are likely to occur is the first step toward improving your performance.

Misunderstanding Key Concepts

A frequent mistake is misunderstanding core principles, which can lead to errors in problem-solving. It’s crucial to thoroughly grasp the foundational concepts before moving on to more advanced topics. Here are some common issues:

• Incorrect Application of Formulas: Often, students mistakenly apply the wrong formula or forget key steps. To avoid this, always double-check which formula is relevant for the specific problem you’re solving.
• Confusion Between Different Shapes: Distinguishing between different shapes and their properties is essential. Ensure you understand the unique characteristics of each figure, such as triangles, quadrilaterals, and circles, to avoid mix-ups during problem-solving.
• Forgetting Units of Measurement: Sometimes, students neglect to convert units or include units in their final answer. Always pay attention to the units of measurement and convert them as needed before finalizing your solution.

Calculation Errors

Calculation mistakes are common when working under pressure or in complex problems. To minimize these errors, follow these steps:

• Rushing Through Problems: Speeding through calculations can result in careless mistakes. Take your time, and if possible, double-check each step before moving on to the next.
• Forgetting to Simplify: Simplification is an important part of solving mathematical expressions. Don’t skip simplifying fractions, radicals, or other expressions, as they may lead to incorrect results.
• Not Checking Work: After completing a problem, take a moment to review your work and verify each calculation. This extra step can often catch minor errors before they become major issues.

Ignoring Problem Conditions

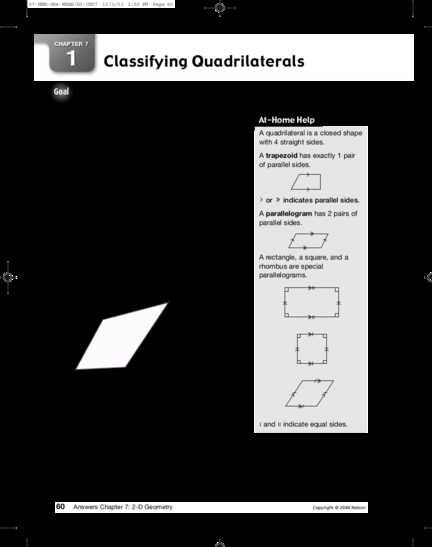
Another common mistake is not fully understanding the problem conditions or misinterpreting what is being asked. Here are some tips to prevent this mistake:

• Missing Key Information: Carefully read through all parts of the problem. Missing even small details can lead to incorrect conclusions. Highlight or underline important information to keep track of key facts.
• Assuming Without Justification: Avoid making assumptions without justification. Every step in your solution should be supported by logical reasoning and evidence from the problem statement.

By being mindful of these common mistakes and following the tips outlined, you can enhance your problem-solving skills and avoid unnecessary errors. Remember, practice and careful attention to detail are the keys to success.

Advanced Problem-Solving Strategies

When approaching complex mathematical tasks, it is essential to apply advanced techniques that go beyond the basic steps. These strategies are designed to help tackle more intricate problems that require a deeper understanding and creative problem-solving methods. By mastering these techniques, you can break down challenging questions into manageable parts and find solutions more efficiently.

In this section, we will explore advanced strategies that will elevate your problem-solving skills. These methods are particularly useful for addressing higher-level problems that involve multiple steps or require you to make connections between different concepts.

Utilizing Symmetry and Transformation

One of the most powerful tools in advanced problem-solving is recognizing and applying symmetry. Symmetry can simplify a problem significantly by revealing hidden relationships between elements of a figure. Key strategies include:

• Reflection and Rotation: Identifying reflective or rotational symmetry in a figure can help you infer properties and relationships that are not immediately obvious. By transforming the figure, you may discover a solution that was previously concealed.
• Translation and Dilatation: Using translations (shifting figures) and dilations (scaling figures) can help simplify the problem and reduce the number of variables you need to consider. These transformations can make geometric relationships clearer and more manageable.

Breaking Down Complex Figures

When dealing with complex figures, it is often helpful to break them down into simpler shapes whose properties are more familiar. This strategy allows you to apply basic formulas and theorems to individual parts of the figure and then combine the results for the overall solution. Consider the following approaches:

• Decomposing into Known Shapes: Decompose complex figures into simpler components such as triangles, rectangles, and circles. By calculating the properties of these basic shapes individually, you can then combine their results for a final answer.
• Using Coordinate Systems: In some problems, placing the figure on a coordinate plane can make it easier to calculate distances, slopes, and other relevant quantities. Coordinate geometry can provide a more straightforward path to the solution, especially when dealing with complex shapes or angles.

By implementing these advanced problem-solving strategies, you can tackle even the most challenging tasks with greater confidence. These techniques help you uncover deeper relationships between figures and simplify otherwise difficult problems, making complex calculations more manageable and intuitive.

Practice Problems for Skill Improvement

Practice is essential for mastering any mathematical concept. In this section, we will explore a range of practice problems designed to reinforce your understanding of key principles and enhance your problem-solving abilities. These exercises cover a variety of topics and difficulty levels, offering a comprehensive way to apply what you’ve learned.

By tackling these problems, you will be able to test your knowledge, identify areas that need further attention, and develop the skills required to solve more advanced tasks. Regular practice helps solidify foundational concepts and prepare you for more challenging scenarios.

Problem Set 1: Basic Concepts

Start with these simpler problems to get comfortable with the fundamental principles. These questions will help you build a strong foundation for more advanced challenges:

Problem	Solution
Find the area of a rectangle with length 8 units and width 5 units.	Area = length × width = 8 × 5 = 40 square units.
Calculate the perimeter of a triangle with sides of 6, 8, and 10 units.	Perimeter = 6 + 8 + 10 = 24 units.

Problem Set 2: Intermediate Challenges

Once you are comfortable with the basics, move on to these intermediate-level problems to refine your understanding:

Problem	Solution
Find the length of the hypotenuse of a right triangle with legs of 7 and 24 units.	Hypotenuse = √(7² + 24²) = √(49 + 576) = √625 = 25 units.
Calculate the area of a circle with a radius of 6 units.	Area = π × radius² = π × 6² = π × 36 ≈ 113.1 square units.

These practice problems will help reinforce key concepts and give you the opportunity to apply them in different contexts. By working through these challenges, you can strengthen your skills and prepare for more advanced topics ahead.

How to Review Mathematical Concepts Effectively

Reviewing mathematical concepts efficiently is essential for solidifying your understanding and improving problem-solving skills. Whether you’re preparing for an exam or just looking to enhance your knowledge, a structured review approach can help you retain key principles and techniques. The process involves focusing on important topics, practicing regularly, and addressing weak areas systematically.

By adopting effective strategies, you can ensure that your review sessions are productive and that you’re well-prepared to tackle both simple and complex problems. This section will outline several methods that can help you review material efficiently, retain information better, and avoid common mistakes during assessments.

1. Break Down Key Concepts

Start by identifying the main concepts covered in your studies. Breaking them down into smaller, manageable parts can make it easier to focus on each area individually. For instance, if working with shapes or figures, categorize them by type (triangles, circles, polygons) and then review specific properties related to each. Here are some tips:

• Focus on one concept at a time.
• Use diagrams to visualize key ideas.
• Create summaries for each topic, outlining formulas, properties, and examples.

2. Practice Consistently with Problem Sets

Regular practice is one of the most effective ways to reinforce learning. Solving problems helps you apply what you’ve learned and highlights areas that require more attention. Consider solving a mix of basic and advanced problems to build confidence and expertise. Here are a few steps to guide your practice:

• Start with easier problems to build confidence.
• Gradually increase the difficulty level as you gain mastery.
• Use practice sets from different sources to expose yourself to various problem types.

By reviewing systematically and consistently practicing, you can sharpen your skills, improve accuracy, and reduce the time it takes to solve problems efficiently. The key is regular engagement with the material and a focus on both strengths and weaknesses.