Edgenuity Geometry Cumulative Exam Answers Guide

Preparing for an important assessment in mathematics can be a daunting task, especially when it involves a range of complex concepts and problem-solving techniques. Whether you’re working through algebraic challenges, spatial reasoning, or applying mathematical theories to real-world situations, understanding the key principles is essential for achieving success. This section is designed to guide you through the process, providing insights and helpful strategies to ensure you’re well-equipped for your upcoming tests.
By familiarizing yourself with core concepts and practicing problem-solving methods, you can build confidence and improve your performance. A solid grasp of essential formulas, visualizing solutions, and managing time effectively are all crucial elements that can make a difference. The following sections will explore valuable tips and resources to help you navigate your studies and tackle challenges with confidence.
Edgenuity Geometry Cumulative Exam Answers
When preparing for a comprehensive assessment that covers a wide range of mathematical topics, understanding key principles and strategies is essential. This section focuses on helping you navigate through different types of problems you might encounter, offering techniques to approach them effectively. A thorough grasp of fundamental concepts, combined with consistent practice, can lead to better performance and a more confident mindset during testing.
Effective Study Techniques for Success
Success in any comprehensive evaluation requires a structured approach to studying. Focus on mastering core topics, ensuring you understand the underlying principles rather than simply memorizing formulas. Practice regularly by working through a variety of problems to familiarize yourself with different question types. Use available resources, such as practice exercises, study guides, and past tests, to reinforce your knowledge and identify areas where improvement is needed.
Problem-Solving Tips for Complex Questions
When facing challenging questions, it’s important to remain calm and focused. Break down each problem step by step, and don’t hesitate to rework it if needed. Remember to use visual aids, like diagrams or graphs, to better understand the problem. Time management is key, so pace yourself and ensure you’re not spending too much time on any single question. With the right approach, complex questions become more manageable and less overwhelming.
Overview of Edgenuity Geometry Exams
Assessments in mathematics often cover a broad spectrum of topics, designed to test students’ understanding of fundamental principles, problem-solving abilities, and analytical thinking. These evaluations are structured to challenge students across different levels, from basic concepts to more complex scenarios that require critical thinking. A strong foundation in key topics is essential for performing well, as the questions may range from simple calculations to more involved, multi-step problems.
Each assessment typically includes a mix of question formats, such as multiple choice, short answer, and application-based problems. These different types of questions aim to test not only knowledge but also the ability to apply concepts in real-world contexts. To succeed, it’s important to develop strategies that help manage time effectively, ensure accuracy, and approach problems with a clear step-by-step method.
Common Challenges in Geometry Exams
Students often encounter a variety of obstacles when tackling complex assessments that test their understanding of mathematical principles. These challenges can arise from several areas, including difficulties in visualizing problems, applying formulas correctly, and managing time effectively during the test. Identifying these common struggles early on and developing strategies to overcome them is crucial for improving performance and boosting confidence.
Difficulty with Visualizing and Drawing Diagrams
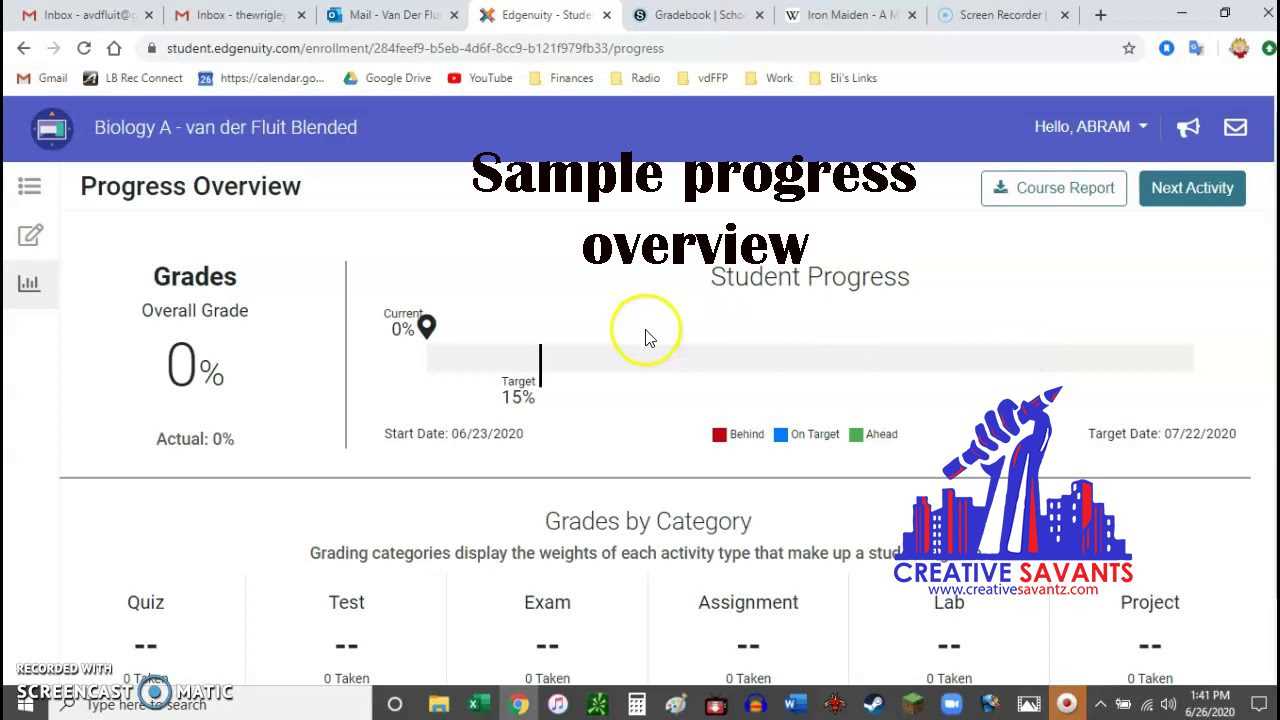
One of the most frequent challenges students face is the ability to visualize and accurately represent problems, especially when dealing with spatial reasoning or shapes. Drawing diagrams can significantly help in understanding the problem, but without practice, it’s easy to misinterpret the question or make mistakes in the drawing process. Developing skills to quickly sketch out accurate representations and recognizing geometric relationships is key to mastering this aspect of the test.
Misapplication of Key Formulas
Another challenge lies in applying the right formulas to solve problems effectively. With a wide range of equations and rules to remember, it’s easy to forget or confuse them, especially under pressure. Proper study habits and consistent practice are essential for reinforcing these formulas, ensuring they are easily recalled when needed.
| Challenge | Solution |
|---|---|
| Visualizing Diagrams | Practice drawing quick, accurate representations of geometric problems to improve spatial awareness. |
| Misapplying Formulas | Review and memorize key formulas regularly to ensure quick recall and correct application. |
| Time Management | Develop a time management strategy by practicing under timed conditions to avoid rushing through questions. |
How to Prepare for Geometry Assessments
Proper preparation is essential for performing well on any challenging test. Success doesn’t just come from cramming the night before; it’s about developing a structured study plan, understanding the core concepts, and applying effective problem-solving techniques. By following a consistent routine and focusing on both theory and practice, you can confidently approach your test and improve your chances of success.
One key aspect of preparation is identifying areas of weakness and dedicating more time to them. Regular practice and review of problems will help reinforce understanding, while taking mock tests under timed conditions can improve both accuracy and speed. Understanding the test format and knowing what to expect can also reduce anxiety and help you stay focused during the actual assessment.
| Preparation Strategy | Action |
|---|---|
| Review Core Concepts | Study essential formulas and principles regularly to strengthen your foundation. |
| Practice with Problems | Work through sample questions and exercises to familiarize yourself with various problem types. |
| Time Management | Simulate real test conditions by practicing with a time limit to improve speed and efficiency. |
| Understand the Test Format | Familiarize yourself with the types of questions and how they are structured to reduce surprises. |
Strategies for Solving Geometry Problems
Successfully solving mathematical problems requires a clear, methodical approach. Whether tackling simple calculations or complex multi-step challenges, the key to success lies in developing strategies that make it easier to understand the problem and apply the correct techniques. By breaking down each task into manageable parts and following a logical sequence, you can improve accuracy and efficiency in your problem-solving process.
Step-by-Step Approach
One effective strategy is to approach each problem step by step. Start by carefully reading the question to understand what is being asked. Then, identify the known information and what needs to be determined. Draw diagrams or visual aids whenever possible, as these can help clarify relationships between different elements and guide you toward the solution. Once the problem is visualized, apply the appropriate formula or method systematically, ensuring each step is completed before moving on to the next.
Check Your Work
After solving the problem, always take a moment to review your work. This may involve double-checking calculations or ensuring that the solution makes sense in the context of the problem. Revising your solution helps catch mistakes and reinforces learning. By checking your work carefully, you minimize the chance of overlooking errors and increase the likelihood of achieving the correct result.
Understanding Key Geometry Concepts
Mastering essential mathematical principles is crucial for solving problems accurately and efficiently. Understanding core concepts such as shapes, angles, measurements, and the relationships between them lays the foundation for tackling more complex challenges. The key to success is not just memorizing formulas, but truly grasping how different elements interact and how to apply these relationships to various scenarios.
One fundamental concept is the understanding of properties of shapes. For example, knowing the differences between triangles, quadrilaterals, and circles, and how their characteristics influence calculations, can make problem-solving more intuitive. Additionally, grasping angle relationships–such as complementary and supplementary angles–helps in finding unknown values more effectively. By focusing on these key ideas, you can build a solid foundation that will support your success in more challenging problems.
Best Resources for Geometry Help
Having access to the right tools and materials is essential for mastering mathematical concepts. Whether you’re looking for in-depth explanations, practice problems, or interactive learning platforms, the right resources can help reinforce your understanding and improve your problem-solving skills. A combination of traditional and digital tools can provide diverse learning methods to suit different needs.
Online Platforms and Tutorials
There are many online resources that offer structured lessons, interactive exercises, and video tutorials. These platforms can provide step-by-step guidance through complex concepts and give you the opportunity to practice at your own pace. Some useful options include:
- Khan Academy – Offers free, comprehensive lessons on various math topics.
- Coursera – Provides courses from top universities that cover foundational principles and advanced topics.
- Brilliant.org – Focuses on interactive learning with real-life problem-solving scenarios.
Books and Study Guides
For those who prefer offline resources, textbooks and study guides remain valuable tools. Many of these books not only explain theoretical concepts but also include practice problems to test your understanding. Some popular options include:
- Geometry for Dummies – A user-friendly book that explains complex topics in simple terms.
- The Art of Problem Solving – Offers a more advanced approach for students looking to deepen their knowledge.
- McGraw-Hill Education Geometry – A comprehensive guide with practice questions and detailed solutions.
Time Management Tips for Geometry Exams
Effective time management is a critical skill for performing well on any challenging test. When faced with a variety of questions and limited time, it’s important to prioritize tasks, stay focused, and avoid spending too much time on any single problem. By implementing strategies to manage your time efficiently, you can ensure that you have enough time to tackle every question without feeling rushed or overwhelmed.
Plan Your Time Before Starting

One of the first steps in managing your time is to have a clear plan. Before diving into the test, take a moment to estimate how much time you should spend on each section or question. Dividing your time wisely helps prevent rushing through questions or spending too long on any one problem. For example, if the test consists of 20 questions and you have 60 minutes, aim to spend around 3 minutes per question. Keep track of time as you go, and adjust if necessary.
Start with Easier Problems
To build momentum and gain confidence, begin with the questions that seem easiest or most familiar. Completing simpler problems first allows you to accumulate points early and manage your time more effectively. After tackling the easier questions, return to more challenging ones when you have more time and mental energy.
Using Practice Tests to Improve Scores
Practice tests are one of the most effective ways to boost performance and build confidence before any major assessment. By simulating test conditions, you not only familiarize yourself with the format and types of questions, but you also get the opportunity to identify areas where you need improvement. Regular practice helps solidify your knowledge and allows you to refine your problem-solving strategies, ultimately improving your overall score.
Incorporating practice tests into your study routine offers several benefits:
- Increased Familiarity – Helps you become comfortable with the test structure and question styles.
- Time Management Skills – Allows you to practice answering questions within the allotted time frame.
- Identify Weak Areas – Highlights topics or problem types where more review or practice is needed.
- Build Confidence – Reduces anxiety by allowing you to practice under conditions similar to the actual assessment.
By taking practice tests regularly, you can track your progress and adjust your study plan accordingly. Aim to review both correct and incorrect answers after each test, as this will help you learn from your mistakes and strengthen your understanding of key concepts.
Key Formulas to Remember for Geometry
In mathematics, formulas are essential tools for solving a variety of problems. They serve as guidelines to calculate unknown values based on known information, making complex tasks simpler and more manageable. Whether you’re working with areas, perimeters, volumes, or angles, understanding and remembering key formulas is crucial for success. Here are some fundamental equations you should always keep in mind.
One of the most important areas to focus on is the calculation of areas and perimeters for different shapes. These formulas allow you to quickly find the size or boundary of various geometric objects, whether they are two-dimensional or three-dimensional. For example:
- Area of a Rectangle: Area = Length × Width
- Area of a Triangle: Area = 1/2 × Base × Height
- Area of a Circle: Area = π × Radius²
- Perimeter of a Rectangle: Perimeter = 2 × (Length + Width)
- Volume of a Cube: Volume = Side³
These are just a few of the most commonly used formulas. As you advance in your studies, you will encounter more complex equations, but the foundation laid by these basic formulas will help you approach any problem with confidence.
How to Approach Multiple-Choice Questions
Multiple-choice questions can often seem tricky, but with the right approach, they can become much more manageable. The key is to remain systematic and strategic in how you read the question, analyze the options, and select the best answer. By following a few proven strategies, you can increase your chances of choosing the correct response, even when you are uncertain.
Read the Question Carefully
The first step in answering multiple-choice questions effectively is to carefully read the question. Sometimes, key details can be hidden in the wording, so take your time to understand what is being asked. Pay attention to keywords that may hint at the correct approach, such as “always,” “never,” “most likely,” or “best.” These clues can help you narrow down the answer choices.
Eliminate Clearly Incorrect Options
Once you’ve understood the question, look at the available options and begin by eliminating any answers that are obviously wrong. This process of elimination can help you focus on the remaining choices and increase the likelihood of selecting the correct one. Even if you’re unsure, removing clearly incorrect answers gives you a better chance of guessing correctly if you need to.
Finally, trust your instincts and try not to overthink your answers. If you have a strong feeling about a choice, go with it. However, always make sure to revisit any questions you’re uncertain about before finalizing your responses.
Tips for Tackling Word Problems Effectively
Word problems can often be the most challenging part of any assessment, as they require not just understanding mathematical concepts but also interpreting written information correctly. These types of questions test your ability to translate real-world scenarios into solvable equations. By following a systematic approach, you can break down these problems into manageable parts and solve them with confidence.
Step-by-Step Approach to Solving Word Problems
The key to tackling word problems effectively is to follow a structured method. Here’s a simple step-by-step guide to help you:
| Step | Action |
|---|---|
| 1 | Read the Problem Carefully – Understand the details before attempting to solve. Look for key information such as numbers, units, and relationships between quantities. |
| 2 | Identify What Is Being Asked – Clarify the goal of the problem. Are you finding a total, a difference, a ratio, or something else? |
| 3 | Translate Words into Mathematical Expressions – Convert the words into numbers, variables, or operations. Use equations, diagrams, or tables if necessary. |
| 4 | Solve the Equation – Perform the necessary calculations step by step. Don’t rush, and check each step for accuracy. |
| 5 | Double-Check Your Solution – Review your solution and make sure it makes sense in the context of the problem. |
Common Pitfalls to Avoid
Even with a clear approach, word problems can still be tricky. Here are a few common mistakes to watch out for:
- Skipping Key Information: Always read the problem carefully to ensure you don’t overlook any important details.
- Misinterpreting Units: Pay attention to units of measurement and ensure they are consistent throughout the problem.
- Rushing the Process: Take your time to understand the problem and check your work before finalizing your answer.
By following these tips and practicing regularly, you can significantly improve your ability to tackle word problems and enhance your problem-solving skills.
Geometry Exam Scoring Explained
Understanding how assessments are scored can help you better prepare and focus your efforts during study sessions. Scoring typically depends on the accuracy of your responses and how well you apply specific concepts to problem-solving. While different assessments might use varying methods, the scoring usually emphasizes understanding, application, and reasoning skills rather than just rote memorization.
Key Elements of Scoring
Most tests will evaluate your performance based on the following key factors:
- Correctness: The most obvious factor is whether your solution is accurate. Full points are awarded for correct answers, while partial credit may be given for steps that are mostly correct.
- Work Shown: Many assessments require you to show your work. This helps evaluators see your thought process and may be taken into account for partial credit.
- Concept Application: The ability to apply learned principles correctly to unfamiliar scenarios is crucial. Understanding how to use formulas, theorems, and logic correctly can make a significant difference in scoring.
Types of Questions and Their Weight
Different question types may carry different point values based on their complexity. For instance, multiple-choice questions often carry fewer points compared to open-ended problems, which require detailed solutions. Here’s a breakdown of typical question types:
- Multiple-Choice: These questions are generally quicker to answer and are weighted lower in the overall score. They test your recognition of correct information.
- Short Answer/Fill-in-the-Blank: These questions assess your ability to recall specific information or apply basic formulas.
- Problem Solving: These questions require you to show your reasoning and application of learned concepts. They are usually the highest in terms of point value.
By understanding the scoring process and focusing on accuracy, clear work, and the proper application of principles, you can approach each question with greater confidence and improve your overall performance on assessments.
What to Do After the Geometry Exam
Once you’ve completed an assessment, it’s important to reflect on your performance and take the necessary steps to ensure continuous improvement. Whether you performed well or encountered challenges, the time after the test offers an opportunity to learn and grow. Here are some key steps to take after finishing an assessment.
1. Review Your Results
After receiving your results, carefully review the feedback to understand what went well and where you may need more practice. This process helps pinpoint areas that need further attention.
- Identify Mistakes: Look for any questions where you made errors or were unsure of your approach. Understanding why a mistake was made is crucial for improvement.
- Understand Correct Answers: Analyze the questions you answered correctly to ensure you understand why those answers were right. This reinforces your knowledge.
- Ask for Clarification: If any feedback or concepts are unclear, don’t hesitate to ask your teacher or tutor for further explanation.
2. Plan for Future Assessments
After reflecting on your performance, develop a plan to improve for future tests. Use the insights gained to guide your next steps in studying.
- Focus on Weak Areas: Allocate more study time to the areas where you struggled the most. Consider using different resources or methods to reinforce these concepts.
- Practice Regularly: Consistent practice is key. Make time for regular problem-solving to build familiarity with the material.
- Review Test-Taking Strategies: Reflect on your approach during the test. Were there any time-management issues or problems you could have approached differently? Fine-tune your strategies for next time.
3. Take Time to Relax
It’s important to give yourself a break after completing a test. Relaxing and recharging helps you return to studying with a clear mind and renewed focus.
- Engage in a Hobby: Take part in activities you enjoy, such as reading, exercising, or spending time with friends, to reduce stress.
- Rest: Ensure you get adequate rest to allow your mind to recover and stay focused in the long term.
By reviewing your results, planning for future assessments, and taking time to relax, you can build a strong foundation for continued success in your studies.
Common Mistakes to Avoid in Geometry
In the world of mathematical problem-solving, there are several pitfalls that can hinder your progress and lead to incorrect conclusions. These mistakes, though often simple, can be easily overlooked if you’re not careful. By understanding and avoiding these common errors, you can improve your problem-solving skills and achieve better results.
1. Misinterpreting Problem Statements
One of the most frequent mistakes is misinterpreting the information given in the problem. It’s easy to overlook key details or assume things that aren’t explicitly stated. To avoid this:
- Read Carefully: Always take the time to thoroughly read the entire problem. Pay attention to the wording, as even small differences in language can change the meaning.
- Highlight Important Information: Mark key values or relationships in the problem that you’ll need to solve it. This helps prevent missing crucial details.
- Identify What’s Being Asked: Clearly define what the problem is asking for. Are you solving for a length, an area, or something else?
2. Forgetting to Apply Formulas Correctly
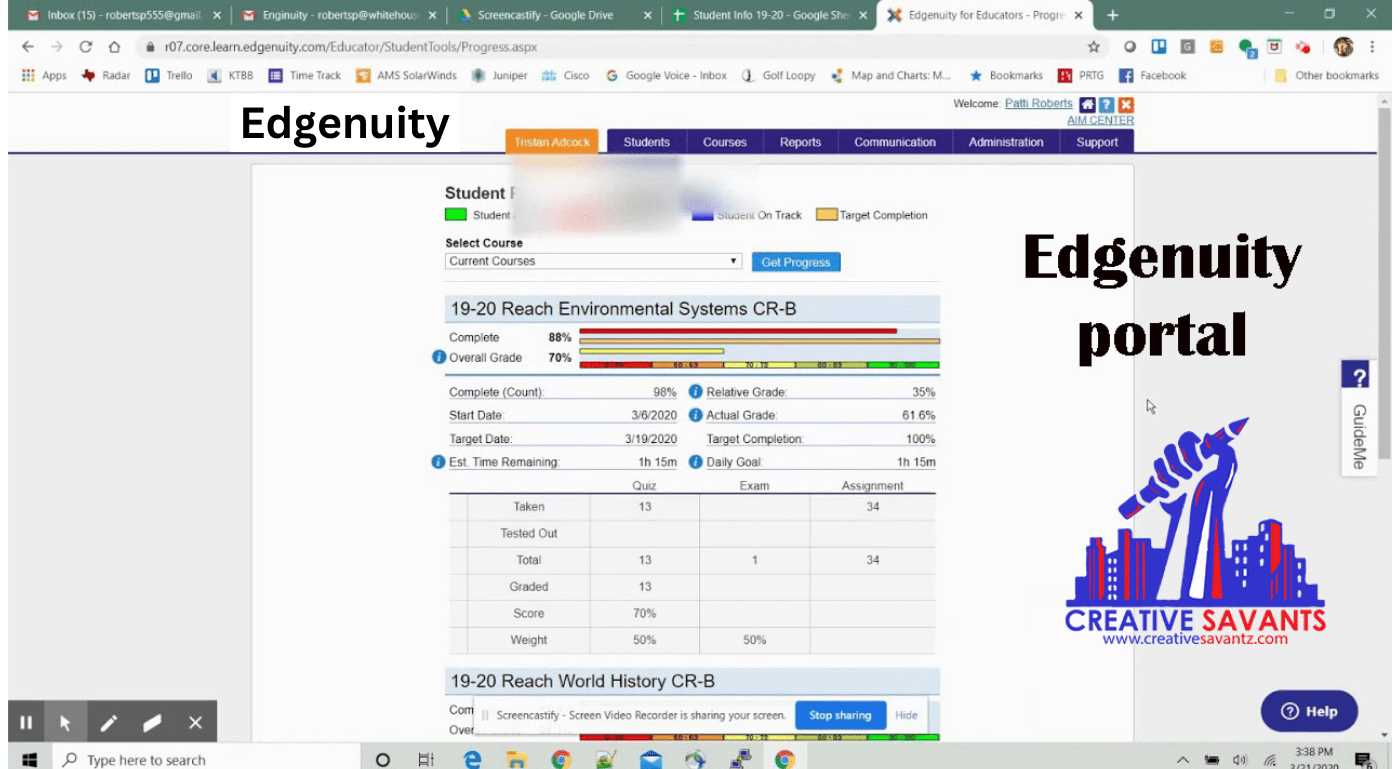
Another common mistake is using formulas improperly or forgetting to apply them altogether. Many problems require specific mathematical relationships, and applying the wrong formula or missing a step can lead to incorrect answers. To avoid this:
- Know Your Formulas: Make sure you’re familiar with the necessary formulas and how they should be applied in various situations.
- Double-Check Your Work: Before finalizing your answer, check that you’ve used the correct formula and substituted the right values.
- Watch Units: Be mindful of units, and always ensure you’re using the right ones throughout the calculation process.
By staying vigilant and methodical in your approach, you can avoid these common mistakes and improve your ability to solve problems accurately and efficiently.
How to Review Geometry Exam Results
Once you’ve completed a mathematical assessment, reviewing the results is a crucial step in understanding your strengths and areas for improvement. By reflecting on your performance, you can identify patterns in your mistakes and adjust your study strategies accordingly. This review process can provide valuable insights into your problem-solving abilities and help you focus on specific areas that need more attention.
1. Analyze Mistakes and Correct Them
Start by carefully going through each question, especially the ones you answered incorrectly. For every mistake, ask yourself what went wrong and how it can be prevented in the future. Consider the following steps:
- Identify Common Errors: Are there certain types of problems you consistently struggle with? This may indicate a specific area that needs more practice.
- Revisit Key Concepts: If you made a mistake due to a misunderstanding of a concept, take the time to review it thoroughly. Understanding the theory behind the problem is key to avoiding similar errors in the future.
- Practice Similar Problems: After identifying your weaknesses, practice similar problems to reinforce your understanding and increase your confidence.
2. Seek Feedback and Guidance
In addition to self-reflection, seeking feedback from teachers, tutors, or classmates can provide additional insights into your mistakes. By discussing your incorrect answers with others, you may gain a different perspective on how to approach similar problems in the future.
It can be helpful to focus on the following:
- Ask for Clarification: If there’s a particular problem or concept that you don’t understand, don’t hesitate to ask for clarification. Teachers or tutors can often explain things in a way that might make more sense.
- Review Solution Strategies: Compare your solutions with the correct ones to see if you missed any critical steps or applied the wrong method.
| Step | Action | Benefit |
|---|---|---|
| 1 | Analyze Mistakes | Helps identify weak areas and avoid future errors |
| 2 | Seek Feedback | Provides new perspectives and helps clarify misunderstandings |
| 3 | Revisit Concepts | Strengthens understanding of the subject matter |
By thoroughly reviewing your results, you’ll be better prepared for future assessments, turning mistakes into valuable learning opportunities.
Boosting Your Geometry Exam Confidence

Building confidence before a math assessment is essential for performing your best. A positive mindset can help you stay calm, focused, and prepared when tackling challenging problems. By developing a strategy for managing your time, reinforcing key concepts, and practicing effective problem-solving techniques, you can approach the test with greater assurance and less anxiety.
1. Practice Regularly and Consistently
Consistent practice is one of the most effective ways to boost confidence. The more you practice, the more familiar and comfortable you’ll become with the material. Here are a few ways to make your practice sessions more efficient:
- Work on a Variety of Problems: Ensure you’re not just focusing on one type of problem. A well-rounded approach helps build confidence in all areas.
- Track Your Progress: Keep a record of your practice sessions to see how much you’ve improved over time. Celebrate small wins to stay motivated.
- Use Timed Practice: Simulate test conditions by setting time limits for yourself. This will help reduce stress and improve your time-management skills.
2. Master Key Concepts and Strategies
Understanding the foundational principles behind the material is crucial for tackling any problem effectively. When you’re confident in your knowledge, you’re less likely to second-guess yourself during the assessment. Consider these tips:
- Review Core Formulas: Ensure you’ve memorized the important formulas and concepts that are frequently used in solving problems.
- Understand the “Why”: Don’t just memorize steps; try to understand the reasoning behind them. This will make it easier to apply your knowledge in various contexts.
- Practice with Study Groups: Studying with peers can offer different perspectives and help you grasp difficult topics more easily.
With regular practice and a solid understanding of core principles, you’ll approach the assessment with confidence and clarity. Remember, confidence comes from preparation–so the more you prepare, the more confident you’ll feel when the time comes to perform.