Algebra 1 Chapter 8 Review Answers and Solutions

In this section, we will dive deep into critical mathematical ideas that are fundamental to solving various types of equations and understanding functions. Mastering these topics will help you build a solid foundation for more advanced problems and ensure success in related areas.

Understanding the core principles involved in solving equations and interpreting graphs is crucial. By breaking down each process step-by-step, you can grasp how different elements interact and how to apply the correct methods to reach a solution. Whether you’re dealing with linear relationships or exploring more complex scenarios, clarity in these foundational skills is key.

Focus will also be placed on common problem-solving strategies to aid in tackling different mathematical challenges. These techniques will help identify patterns and simplify seemingly difficult problems, making them more approachable and easier to solve. With practice and familiarity, you’ll develop the skills to tackle even the most intricate tasks with confidence.

Algebra 1 Chapter 8 Review Answers

This section provides a comprehensive breakdown of key problem-solving methods and techniques essential for mastering core mathematical concepts. By examining various types of equations and expressions, we aim to clarify the necessary steps to achieve accurate results. The following solutions highlight the most effective strategies to handle linear equations, graphing, and system-solving challenges.

Key Techniques and Problem-Solving Approaches

Understanding how to approach problems systematically is fundamental to success. Here are some essential techniques to keep in mind:

• Identifying the right equation type: Recognizing whether you are working with linear, quadratic, or other forms helps in choosing the best method.
• Breaking down complex expressions: Simplify terms and isolate variables to make the solution process more manageable.
• Graphing solutions: Visualizing the relationships between variables often provides clarity and insights into the solution.

Common Mistakes to Avoid

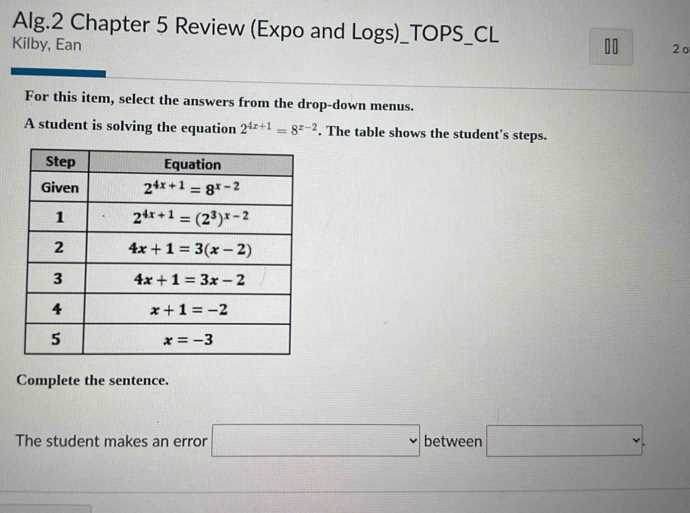
While working through problems, it’s easy to make simple errors that can lead to incorrect results. Here are a few common pitfalls to watch out for:

1. Forgetting to simplify expressions before solving.
2. Incorrectly interpreting the slope or intercept when graphing.
3. Misapplying formulas or mixing up signs during calculations.

By staying aware of these challenges and focusing on the correct methods, you can approach each problem with confidence and accuracy.

Key Concepts in Chapter 8

In this section, we will focus on the core ideas that are essential to solving various types of mathematical problems. These concepts provide the foundation for understanding how to manipulate equations, graph relationships, and solve systems. Mastering these will allow you to confidently tackle problems and deepen your understanding of more advanced topics.

Core Mathematical Principles

The following concepts are vital for progressing in this area of study:

• Linear Relationships: Identifying the relationship between variables and understanding how they interact is crucial for solving equations and graphing.
• Equations of Lines: Understanding slope and intercept helps in determining the equation of a line and graphing it correctly.
• Solving Systems: Learning how to find solutions for multiple equations simultaneously is key for solving real-world problems.

Techniques for Effective Problem Solving

When applying the core principles, it’s important to use the following methods to ensure accuracy and efficiency:

1. Simplification: Break down complex expressions into simpler terms to avoid errors during calculations.
2. Graphing: Plot points on a coordinate plane to visually represent relationships and solutions.
3. Substitution and Elimination: Use these methods to solve systems of equations and find the intersection points.

By mastering these key concepts and techniques, you will be well-equipped to approach a variety of problems with confidence and accuracy.

Step-by-Step Solution Breakdown

Understanding how to approach and solve mathematical problems involves breaking down each step methodically. By following a clear process, you can simplify complex equations and ensure you arrive at the correct result. This section will guide you through each phase of problem-solving, helping you to develop a structured approach that can be applied to different types of equations.

Each solution is broken into individual steps that demonstrate how to isolate variables, simplify expressions, and interpret the results. This approach ensures you understand the reasoning behind each action and can apply it to similar problems in the future.

The key to effective problem-solving is recognizing the relationship between each step and applying the appropriate techniques. Whether you’re solving for a single variable or working with systems, following a logical progression will improve accuracy and efficiency.

Understanding Functions in Algebra 1

Functions are a fundamental concept in mathematics, providing a way to describe relationships between two sets of values. At their core, functions show how each input corresponds to exactly one output. Grasping this idea is essential for solving equations and understanding more complex mathematical concepts.

In this section, we will explore how to identify and work with functions, emphasizing the importance of recognizing independent and dependent variables. By understanding the structure of functions, you’ll be able to solve equations more efficiently and interpret their solutions in a meaningful way.

Functions can be represented in various forms, including equations, graphs, and tables. Knowing how to manipulate these representations allows you to analyze relationships between variables and predict outcomes with precision.

Solving Linear Equations Explained

Solving linear equations is a critical skill that allows you to find the value of an unknown variable. These types of problems typically involve equations where the highest power of the variable is one, making them simpler to solve compared to other forms of equations. Understanding the process behind solving these equations is essential for tackling more complex problems in the future.

The process of solving linear equations involves isolating the variable on one side of the equation through a series of logical steps. Below are the general steps for solving these types of equations:

1. Combine like terms: Simplify both sides of the equation by adding or subtracting similar terms.
2. Isolate the variable: Move terms with the variable to one side and constants to the other side.
3. Simplify the equation: Continue simplifying until you have the variable alone on one side.
4. Check your solution: Always substitute the value of the variable back into the original equation to ensure it satisfies the equation.

By following these steps, you can easily solve linear equations and gain a deeper understanding of mathematical relationships.

Graphing Techniques for Linear Functions

Graphing is an essential skill for visualizing relationships between variables. When dealing with linear functions, it is important to understand how to represent these relationships accurately on a coordinate plane. This section will explore various methods to graph these functions and ensure you can clearly interpret the results.

Key Graphing Methods

There are different strategies for graphing linear functions, but the most common methods include using slope and intercepts or plotting points directly. Each approach allows you to quickly sketch the line and analyze the relationship between the variables.

• Slope-Intercept Form: One of the easiest ways to graph is using the slope-intercept form, which expresses the function as y = mx + b, where m is the slope and b is the y-intercept.
• Point-Slope Method: If you know a point on the line and the slope, you can use the point-slope formula to graph the function.

Example Table: Graphing a Linear Function

Below is an example of how you can plot points for the function y = 2x + 3.

x	y = 2x + 3
-2	-1
-1	1
0	3
1	5
2	7

Using the points from the table, you can plot them on a graph to draw a straight line that represents the function. This method helps to visually understand the behavior of the equation and its solutions.

Applying Slope and Intercepts

Understanding how to apply slope and intercepts is essential for working with linear relationships. These two key elements allow you to describe the direction and position of a line on a graph, making it easier to analyze patterns and predict outcomes. By mastering these concepts, you can solve problems more efficiently and gain deeper insights into the behavior of linear functions.

Using Slope in Real-World Problems

The slope of a line represents the rate of change between the variables, telling you how one variable changes in relation to the other. In many real-world applications, slope can be interpreted as speed, growth rate, or cost per unit. For example:

• Speed: The slope can indicate how fast something is moving. A steeper slope means a higher speed.
• Cost Analysis: Slope can represent the cost per item when graphing expenses versus quantity.

Understanding the Role of Intercepts

Intercepts are the points where the line crosses the axes. The y-intercept shows the starting value when the independent variable is zero, while the x-intercept indicates when the dependent variable is zero. These points are crucial for understanding the behavior of the function at key values.

For example: In a business scenario, the y-intercept could represent the initial cost before any products are sold, while the x-intercept might show when sales reach a point where costs break even.

By using slope and intercepts together, you can effectively model relationships and solve for unknown values in various practical applications.

Working with Systems of Equations

Systems of equations involve solving for multiple unknowns at the same time, often with more than one equation. By finding the values that satisfy all equations in the system simultaneously, you can identify the solution to the problem. These types of problems are commonly encountered in real-world scenarios, such as calculating the point of intersection between two different quantities or determining optimal solutions in various fields like economics and engineering.

Methods for Solving Systems

There are several methods for solving systems of equations, each with its advantages depending on the nature of the equations. Below are the most commonly used approaches:

• Substitution: In this method, you solve one equation for one variable and substitute that expression into the other equation. This process reduces the system to a single equation with one variable, making it easier to solve.
• Elimination: This approach involves adding or subtracting equations to eliminate one of the variables, leaving you with a simpler equation to solve. Once one variable is found, you can substitute it back to find the other variable.
• Graphing: By graphing both equations on a coordinate plane, the point where the lines intersect represents the solution to the system. This method is more visual but can be less precise unless the intersection point has integer coordinates.

Practical Applications of Systems

Systems of equations are powerful tools for solving problems in various real-life contexts. For example:

• Business: Systems can be used to model supply and demand, helping companies determine the best price point or quantity of goods to produce.
• Travel: By using systems, you can calculate time and distance for multiple trips with different speeds or routes.

Understanding how to work with systems of equations gives you the ability to solve complex problems and analyze different situations systematically and efficiently.

Solving Word Problems Effectively

Word problems often require translating a real-world situation into a mathematical model. To solve them successfully, it’s important to break down the problem step by step, identify the key elements, and apply the correct methods. Mastering this process allows you to approach complex scenarios with confidence and find solutions efficiently.

Steps for Tackling Word Problems

Here is a simple approach to help solve word problems effectively:

1. Read the Problem Carefully: Make sure you fully understand the situation. Identify key information such as numbers, relationships, and what is being asked.
2. Define the Variables: Choose symbols to represent unknown quantities. This step is crucial for translating the problem into a mathematical equation.
3. Set Up the Equation: Translate the problem into one or more equations based on the relationships described in the problem.
4. Solve the Equation: Use appropriate methods to solve for the unknown variable(s).
5. Check Your Solution: Verify that your answer makes sense in the context of the problem and that it satisfies all conditions given in the problem.

Common Types of Word Problems

Word problems can vary widely depending on the context. Some common types include:

• Mixture Problems: Involve combining different quantities to form a new mixture with specific properties (e.g., blending two liquids to get a desired concentration).
• Rate Problems: Deal with concepts such as speed, distance, and time, often requiring you to apply the formula distance = rate × time.
• Work Problems: Involve calculating how long it will take to complete a task based on the rate at which work is being done (e.g., two people working together on a project).

By practicing these steps and understanding common types of word problems, you will be able to approach a wide variety of real-world situations and solve them with confidence.

Exploring Inequalities and Solutions

Inequalities are expressions that describe a range of possible solutions rather than a single value. Unlike equations, which focus on finding exact solutions, inequalities represent relationships between quantities where one side is greater than, less than, or not equal to the other. Understanding how to manipulate and solve these expressions is essential in many areas of mathematics and real-world applications.

Solving Linear Inequalities

Linear inequalities involve expressions with variables raised to the first power. The process of solving these inequalities is similar to solving equations, with a few important differences:

• Isolate the Variable: Just like with equations, the first step is to isolate the variable on one side of the inequality.
• Flip the Inequality Sign: If you multiply or divide both sides of the inequality by a negative number, you must reverse the inequality sign to maintain the balance of the statement.
• Graphing the Solution: Once the inequality is solved, you can represent the solution on a number line, shading the appropriate region that satisfies the inequality.

Types of Inequalities

There are several types of inequalities that you may encounter:

• Greater Than and Less Than: These inequalities simply compare two expressions, such as x > 3 or y .
• Greater Than or Equal To, Less Than or Equal To: These inequalities include a line under the inequality symbol, indicating that the solution set includes the boundary value, such as x ≥ 4.
• Compound Inequalities: These involve two inequalities joined by “and” or “or,” such as -3 ≤ x or x 5.

Mastering the manipulation and solution of inequalities provides a foundation for tackling more complex mathematical concepts and real-world problem-solving scenarios.

Properties of Linear Functions

Linear functions are fundamental in understanding relationships between variables. These functions describe a constant rate of change and produce straight lines when graphed. Identifying the properties of linear functions helps in analyzing their behavior and solving various types of problems efficiently. Key attributes such as slope, intercepts, and the general form of the function provide insight into the nature of the relationship between the variables.

Slope and Rate of Change

The slope of a linear function represents the rate of change between two variables. It indicates how much the dependent variable changes for each unit increase in the independent variable. The slope is calculated as the ratio of the vertical change to the horizontal change between two points on the graph, often denoted as m.

• Positive Slope: A positive value for the slope means the function is increasing as the independent variable increases.
• Negative Slope: A negative value indicates the function is decreasing as the independent variable increases.
• Zero Slope: A slope of zero means the function is horizontal, showing no change in the dependent variable.
• Undefined Slope: An undefined slope occurs when the line is vertical, meaning the independent variable does not change.

Intercepts and Graphing

The intercepts of a linear function are the points where the graph intersects the axes. These points are crucial for sketching the graph and understanding the function’s behavior.

• Y-intercept: The point where the graph crosses the vertical axis. This occurs when the independent variable is zero.
• X-intercept: The point where the graph crosses the horizontal axis. This occurs when the dependent variable is zero.

By understanding the slope and intercepts, you can easily graph a linear function and interpret its behavior in various applications. These properties are the foundation for solving equations and modeling real-world situations where relationships between quantities are linear.

Factoring Strategies for Algebra

Factoring is an essential skill in mathematics that involves breaking down expressions into simpler components. By factoring expressions, you can solve equations, simplify problems, and understand relationships more clearly. Several strategies are commonly used to factor different types of expressions effectively, and knowing when and how to apply them is crucial for mastering this concept.

Common Factoring Methods

There are various methods for factoring expressions, each suited to specific types of problems. Understanding these techniques will help you approach problems with confidence:

• Factoring out the Greatest Common Factor (GCF): The first step in factoring any polynomial is to look for the greatest common factor of all terms. This method involves dividing each term by the GCF and factoring it out to simplify the expression.
• Factoring Trinomials: When you have a trinomial of the form ax² + bx + c, you can factor it into two binomials. This method often involves finding two numbers that multiply to ac and add to b.
• Difference of Squares: This strategy applies when you have two terms that are perfect squares. The expression can be factored into the form (a + b)(a – b).
• Perfect Square Trinomials: If the expression is a perfect square trinomial, it can be factored as (a + b)² or (a – b)², where a and b are the square roots of the terms.

Solving Equations Using Factoring

Once an expression is factored, you can use it to solve equations. The factored form allows you to set each factor equal to zero and solve for the variable. This method, known as the zero-product property, is particularly useful when dealing with quadratic equations and higher-order polynomials.

• Example: If you have the equation (x – 3)(x + 2) = 0, you can set each factor equal to zero and solve for x, giving the solutions x = 3 and x = -2.

By practicing these strategies, you can improve your ability to factor and solve a wide variety of problems. Factoring is not only an important skill in solving equations but also in simplifying complex expressions for further analysis.

Analyzing Quadratic Equations

Understanding the structure and behavior of quadratic equations is crucial in solving a variety of mathematical problems. These equations typically involve squared terms and can represent a wide range of real-world scenarios, from projectile motion to financial modeling. By analyzing their components, you can determine key properties such as their roots, vertex, and direction of opening. This analysis provides insights into how the equation behaves graphically and how to solve it efficiently.

Key Components of a Quadratic Equation

A standard quadratic equation is expressed in the form ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. To analyze a quadratic equation, it’s important to examine several key features:

Feature	Description
Roots (Solutions)	The values of x that make the equation true, which can be found using the quadratic formula or factoring.
Vertex	The highest or lowest point on the graph of the equation, depending on the sign of a.
Axis of Symmetry	The vertical line that divides the parabola into two equal halves, passing through the vertex.
Direction of Opening	Determined by the sign of a>: if a is positive, the parabola opens upwards; if negative, it opens downwards.

Methods for Solving Quadratic Equations

There are several methods to solve quadratic equations, each suited for different forms of the equation. The most common approaches include:

• Factoring: If the equation can be factored, set each factor equal to zero and solve for x.
• Quadratic Formula: The quadratic formula x = (-b ± √(b² – 4ac)) / 2a is a general method that works for all quadratic equations, even if they cannot be factored easily.
• Completing the Square: This method involves transforming the quadratic into a perfect square trinomial and then solving for x.

By understanding these key components and solving methods, you can effectively analyze and solve any quadratic equation. This process not only helps in finding the solutions but also in understanding the graph of the equation, making it easier to visualize and interpret real-world applications.

Evaluating Expressions with Exponents

When working with mathematical expressions, exponents play a crucial role in simplifying and solving problems. An exponent represents the number of times a base is multiplied by itself. Evaluating expressions with exponents involves applying the rules of exponents to compute the value of a given expression efficiently. This process is essential for solving equations and understanding the properties of powers.

Basic Exponent Rules

To evaluate expressions involving exponents, it’s important to understand some key rules that govern how exponents work. Here are the main exponent properties:

• Product Rule: When multiplying two numbers with the same base, add their exponents. For example, aⁿ × aᵐ = aⁿ⁺ᵐ.
• Quotient Rule: When dividing two numbers with the same base, subtract the exponent of the denominator from the exponent of the numerator. For example, aⁿ ÷ aᵐ = aⁿ⁻ᵐ.
• Power Rule: When raising a power to another power, multiply the exponents. For example, (aⁿ)ᵐ = aⁿᵐ.
• Zero Exponent Rule: Any nonzero number raised to the power of zero equals one. For example, a⁰ = 1.
• Negative Exponent Rule: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, a⁻ⁿ = 1/aⁿ.

Steps for Evaluating Expressions

To evaluate an expression with exponents, follow these general steps:

1. Simplify the base: If the base contains any parentheses, simplify the expression inside the parentheses first.
2. Apply exponent rules: Use the appropriate exponent rule (product, quotient, etc.) to simplify the expression further.
3. Perform calculations: Carry out any multiplication, division, or addition/subtraction as needed to find the final value.

By applying these rules and steps, you can evaluate expressions involving exponents quickly and accurately. This skill is foundational in higher-level mathematics and is used in a variety of real-world applications, such as science and engineering.

Understanding Absolute Value Equations

Absolute value equations involve expressions where the variable is within absolute value symbols. The concept of absolute value refers to the distance a number is from zero on the number line, regardless of direction. This means that any number, whether positive or negative, has the same absolute value. Solving absolute value equations requires understanding how to handle both the positive and negative solutions that emerge when the absolute value is removed.

Key Concepts in Absolute Value Equations

When solving equations with absolute values, it’s important to recognize that the equation can result in two possible outcomes: one where the expression inside the absolute value equals the positive value, and one where it equals the negative value. Here are the steps to follow:

• Isolate the absolute value expression: First, ensure the absolute value expression is alone on one side of the equation.
• Set up two equations: Once the absolute value is isolated, create two separate equations–one where the expression inside the absolute value is set equal to the positive value, and another where it’s set equal to the negative value.
• Solve both equations: Solve each equation individually to find the possible solutions.

Example of Solving an Absolute Value Equation

Consider the equation: |x – 3| = 5. To solve this equation, follow these steps:

1. Remove the absolute value: Write two separate equations: x – 3 = 5 and x – 3 = -5.
2. Solve both equations:
   • For x – 3 = 5, add 3 to both sides: x = 8.
   • For x – 3 = -5, add 3 to both sides: x = -2.
3. Check the solutions: Both x = 8 and x = -2 satisfy the original equation, so both are valid solutions.

Understanding absolute value equations is crucial for solving a variety of problems in mathematics, especially when dealing with real-world situations where distance or magnitude is always considered as a positive value, regardless of direction.

Common Mistakes to Avoid

When solving mathematical problems, especially those involving equations and functions, it’s easy to make small errors that can lead to incorrect results. Recognizing common pitfalls can help improve accuracy and efficiency. Many of these mistakes arise from misunderstanding key concepts or overlooking important steps in the process. Being aware of these errors is the first step toward mastering problem-solving techniques.

1. Ignoring Proper Order of Operations

One of the most frequent mistakes occurs when the order of operations is not followed correctly. The proper sequence should be:

• Parentheses – Solve expressions inside parentheses first.
• Exponents – Evaluate exponents next.
• Multiplication and Division – From left to right.
• Addition and Subtraction – From left to right.

Skipping or rearranging these steps can lead to incorrect answers, especially when handling complex expressions.

2. Forgetting to Distribute Properly

When dealing with terms inside parentheses, it’s essential to apply the distributive property correctly. For example, in the expression 2(x + 3), failing to multiply the 2 by both x and 3 results in an incomplete simplification. Always remember to distribute each term to all parts within the parentheses.

3. Misinterpreting Negative Signs

Negative signs can be tricky, particularly when dealing with multiple terms or operations. A common mistake is to incorrectly handle negative numbers during addition or subtraction. For example, in the expression -5 + 3, the correct answer is -2, not 2. Always double-check the signs when simplifying equations.

4. Incorrectly Solving for the Variable

Another error is failing to isolate the variable correctly when solving an equation. This often happens when additional terms or operations are not correctly reversed. For instance, when solving 2x + 5 = 11, forgetting to subtract 5 from both sides before dividing by 2 will result in an incorrect solution. Always perform each operation step by step and ensure the variable is isolated properly.

5. Overlooking Special Cases

Some equations or functions have special conditions or solutions that are easy to overlook. For example, when solving quadratic equations, it’s important to remember that some solutions may not be real numbers. Similarly, equations involving absolute values require separate cases for positive and negative results. Always consider all possible scenarios and solutions.

By being mindful of these common errors, you can improve your problem-solving skills and increase your understanding of mathematical concepts.

Review Resources and Study Tips

To excel in solving mathematical problems and grasping key concepts, it’s essential to utilize the right study materials and strategies. Having a structured plan, along with the right resources, can help reinforce your understanding and boost performance. Whether you’re reviewing specific techniques or strengthening your problem-solving skills, these tools and tips can guide you through the learning process.

Effective Study Resources

Here are some helpful tools and materials to enhance your study sessions:

Resource	Description	Benefit
Textbooks and Workbooks	Comprehensive guides with theory and practice problems.	Provides a solid foundation and a wide range of exercises.
Online Tutorials and Videos	Interactive lessons and step-by-step video explanations.	Helps visualize concepts and understand complex problems easily.
Practice Worksheets	Printed or digital worksheets filled with practice problems.	Allows you to reinforce learned techniques through repetition.
Math Apps and Tools	Apps for solving equations, graphing, and checking solutions.	Quick feedback on answers, aiding faster problem-solving.

Study Tips for Success

Here are several strategies to help maximize your review sessions:

• Break Down Complex Problems: Start with simple examples and gradually move to more difficult ones. This helps build confidence and understanding.
• Practice Regularly: Consistent practice is essential for mastering any topic. Dedicate time each day to solving problems to keep skills sharp.
• Ask for Help: If you encounter difficulties, don’t hesitate to seek assistance from a teacher, tutor, or online community.
• Focus on Mistakes: Review any errors you make during practice. Understanding why a solution is incorrect helps reinforce the correct method.
• Summarize Key Concepts: Create quick reference notes or flashcards summarizing essential formulas and rules. This aids in quick recollection.
• Work in Study Groups: Group study allows for the sharing of strategies and solutions, helping you understand different approaches to solving problems.

By incorporating these resources and strategies into your routine, you can optimize your review process and strengthen your mathematical knowledge.