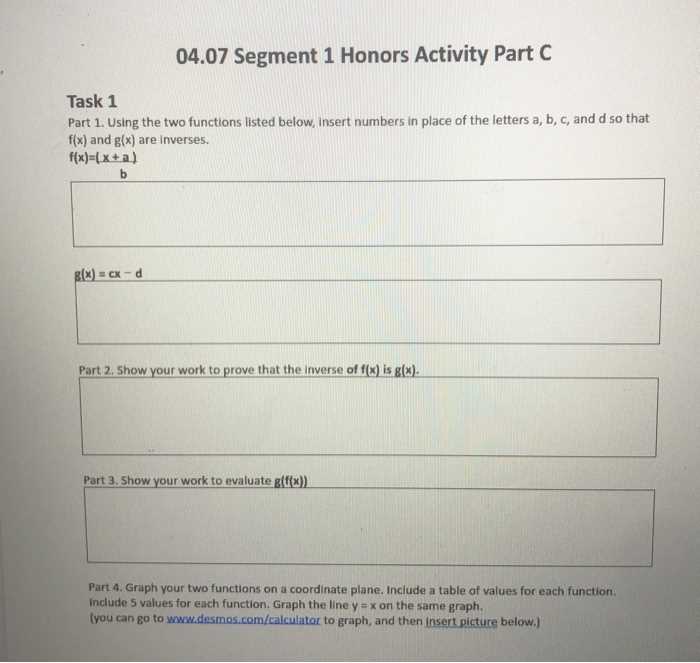
Flvs Algebra 1 Segment 1 Exam Answers

In the first stage of your mathematical learning journey, you will encounter essential concepts that lay the groundwork for more advanced topics. This phase focuses on developing a strong foundation, allowing you to approach more complex problems with confidence. A thorough understanding of basic principles is crucial for success in any future challenges.
Throughout this section, you will tackle fundamental operations and techniques that are applicable in various mathematical contexts. It is important to grasp these concepts thoroughly, as they are essential building blocks for future topics. By honing your skills here, you prepare yourself for more intricate calculations and problem-solving strategies.
Preparation is key to mastering this material. By practicing various types of problems and refining your methods, you will improve both your speed and accuracy. In addition, a strategic approach to learning will help you retain information more effectively, ensuring long-term success.
As you work through the material, remember that consistent effort and a methodical approach are your best tools. Focus on understanding the reasoning behind each solution, rather than simply memorizing formulas. This mindset will serve you well as you progress through more challenging topics.
Flvs Algebra 1 Segment 1 Exam Answers
In the initial stage of your mathematical journey, mastering key concepts is essential for building a strong foundation. This phase involves practicing basic problem-solving techniques, ensuring you are prepared for more advanced challenges. By focusing on core principles, you can develop a deeper understanding of how to approach complex problems effectively.
Key Topics to Focus On
During this section, you will work through important principles such as basic equations, operations, and the structure of mathematical expressions. Understanding these elements will not only help you perform calculations accurately but also allow you to tackle real-world problems with ease. Repetition and consistent practice are vital to mastering these concepts and ensuring long-term retention.
Strategies for Success
To excel in this phase, focus on solving a variety of practice problems. Breaking down each challenge step by step will help you grasp the reasoning behind each solution. In addition, review common pitfalls and develop strategies to avoid common mistakes. This approach will sharpen your critical thinking skills and build confidence as you progress through more difficult topics.
Overview of Algebra 1 Segment 1
In the early stages of this mathematical course, you will encounter foundational concepts that are essential for understanding more complex ideas in the future. This part of the course is designed to introduce you to key problem-solving techniques and mathematical operations. Mastery of these basics will serve as the cornerstone for advancing through more challenging material.
Throughout this section, you will focus on understanding expressions, manipulating variables, and solving simple equations. Gaining a solid grasp of these skills is crucial, as they are used repeatedly in later lessons. Building confidence in these fundamental areas will enable you to approach progressively difficult topics with ease and accuracy.
Consistency in practice is vital for retaining these concepts. By regularly engaging with problems and reviewing solutions, you will solidify your understanding and improve your problem-solving speed. Each exercise offers an opportunity to sharpen your skills and identify areas for improvement.
Key Topics Covered in Segment 1
This initial phase introduces you to the fundamental building blocks of mathematical problem-solving. Understanding these core topics will provide the necessary foundation for tackling more complex problems later on. The focus is on developing a strong grasp of basic operations, patterns, and relationships between numbers.
Understanding Mathematical Expressions

A key area of focus is learning how to work with expressions, which form the basis for many types of equations and real-world problems. You’ll become familiar with terms, coefficients, and variables, and how to manipulate them effectively. This skill is vital for simplifying and solving various mathematical scenarios.
Solving Simple Equations and Inequalities
Another critical topic is solving basic equations and inequalities. You’ll learn the step-by-step process of isolating variables and balancing both sides of an equation. Mastering this skill is essential, as it is applied in a wide range of mathematical contexts, from basic arithmetic to more advanced problem-solving tasks.
Understanding Algebraic Expressions and Equations
At the heart of problem-solving in mathematics lies the ability to interpret and manipulate mathematical expressions and relationships. These are fundamental tools that allow us to describe and solve a wide range of real-world situations. Grasping the structure and components of these expressions will enable you to break down complex problems into manageable parts.
What are Mathematical Expressions?
Mathematical expressions consist of numbers, variables, and operators that are combined to represent a specific value or relationship. The key elements of an expression include:
- Variables: Symbols, usually letters, that represent unknown quantities.
- Coefficients: Numbers that multiply the variables.
- Operators: Symbols like addition (+), subtraction (-), multiplication (×), and division (÷) that define the relationship between terms.
Understanding how to manipulate these components is crucial for simplifying expressions and solving equations.
Solving Simple Equations
Equations represent relationships between expressions. In an equation, two expressions are set equal to each other, and the goal is to find the value of the variable that makes the equation true. Here are the basic steps involved in solving an equation:
- Identify the variable: Determine which symbol in the equation represents the unknown value.
- Isolate the variable: Use inverse operations (such as addition and subtraction or multiplication and division) to move other terms to the opposite side of the equation.
- Solve for the variable: Perform the necessary calculations to find the value that satisfies the equation.
By practicing these steps, you can gain confidence in solving equations and apply these techniques to more advanced topics later on.
How to Solve Linear Equations

Solving linear equations is one of the most fundamental skills in mathematics. These equations are defined by the presence of a variable raised to the first power, and the goal is to find the value of that variable that satisfies the equation. Mastering this skill will not only help you solve a wide range of problems but will also lay the foundation for more advanced topics in mathematics.
The key to solving linear equations is to isolate the variable on one side of the equation. This process involves performing a series of operations to simplify the equation, step by step, until the variable stands alone. The operations used to solve these equations are basic arithmetic operations like addition, subtraction, multiplication, and division.
Step-by-step approach:
- Identify the equation: Start by recognizing the equation you are working with, which will have a variable and constants on either side of the equation.
- Move constants to one side: Use addition or subtraction to move any constants (numbers) to one side of the equation.
- Isolate the variable: Use multiplication or division to isolate the variable on one side of the equation.
- Simplify: Once the variable is isolated, simplify the equation if needed to find the solution.
By practicing these steps with a variety of equations, you’ll develop a strong understanding of how to solve linear problems efficiently. Each equation may present slight variations, but the fundamental steps remain the same.
Important Concepts for the FLVS Exam
To succeed in this stage of the course, it is crucial to understand the core principles that will be tested. These fundamental ideas form the basis for more advanced topics and are essential for solving a wide range of problems. Being familiar with these concepts will not only help you perform well but also give you the confidence to approach new challenges as you continue learning.
Key topics to focus on include problem-solving strategies, basic operations with variables, and understanding the relationships between different mathematical expressions. Mastery of these concepts will enable you to handle various types of questions and apply the right techniques efficiently. Recognizing patterns and learning to break down complex problems into simpler steps are also critical skills.
Core areas to review:
- Equations: Understanding how to solve and manipulate simple equations is essential.
- Expressions: Knowing how to work with and simplify expressions will help you solve a variety of problems.
- Operations: Familiarity with basic arithmetic and the order of operations is fundamental for solving equations and simplifying expressions.
- Graphing: Basic graphing skills are useful for visualizing solutions and interpreting relationships between variables.
By focusing on these core areas, you will be well-prepared to approach each challenge with a methodical mindset, ensuring that you can solve problems accurately and efficiently.
Practice Questions for Segment 1
To reinforce your understanding of the material, it’s essential to work through practice problems. These questions help solidify key concepts and provide an opportunity to apply what you’ve learned. By regularly practicing with different types of problems, you will enhance your problem-solving abilities and prepare yourself for future challenges.
Sample Questions to Test Your Skills
Here are a few questions that will help you evaluate your comprehension of the basic concepts. Attempt to solve these problems step by step, and remember to double-check your answers for accuracy:
- Solve for x: 3x + 5 = 20
- Simplify the expression: 2a + 4b – 3a + 6b
- What is the solution to the equation: 5(x – 4) = 20?
- Write the expression for the perimeter of a rectangle with length 3x and width 4y.
Tips for Practicing
While solving these questions, keep the following tips in mind:
- Work methodically: Break each problem into smaller steps and solve one part at a time.
- Use inverse operations: When solving for a variable, always perform the opposite operation to isolate the unknown.
- Double-check your work: After solving, review your steps to ensure that you didn’t make any mistakes along the way.
By consistently practicing with questions like these, you will develop a deeper understanding of the material and be better prepared for more complex topics in the future.
Common Mistakes to Avoid in Algebra 1
When working through mathematical problems, certain errors are commonly made, especially by those new to working with equations and expressions. Understanding these pitfalls and how to avoid them is key to improving your skills and ensuring accuracy in your work. Recognizing these mistakes early on can help you develop a more effective approach to problem-solving.
Below are some of the most frequent mistakes students make, along with tips on how to avoid them:
Key Mistakes to Watch Out For
- Forgetting to apply the distributive property: A common mistake occurs when students forget to distribute a term across parentheses. Always remember to multiply the outer term by every term inside the parentheses.
- Mixing up the order of operations: Failing to follow the correct sequence of operations (PEMDAS) can lead to incorrect answers. Be sure to simplify expressions in the correct order: Parentheses, Exponents, Multiplication and Division (left to right), and Addition and Subtraction (left to right).
- Not simplifying expressions fully: Sometimes students stop simplifying once they’ve completed part of the problem. Always ensure that your final expression is as simplified as possible.
- Incorrectly solving for the variable: When isolating the variable, it’s important to perform the same operation on both sides of the equation. Neglecting this step can lead to incorrect results.
- Misplacing signs: Negative signs often cause confusion. Be sure to carefully track positive and negative numbers when solving equations, especially when adding or subtracting terms.
How to Avoid These Mistakes
- Double-check your work: After solving a problem, revisit each step to ensure accuracy. A quick review can catch simple errors before they affect your solution.
- Write out each step: Don’t skip steps, even when they seem obvious. Writing out every step helps you track your progress and ensures that no important detail is overlooked.
- Practice consistently: The more you practice, the more familiar you become with common problem types. Consistent practice helps reduce the chance of making these errors.
By being aware of these mistakes and taking steps to avoid them, you can greatly improve your problem-solving ability and enhance your understanding of the material.
Step-by-Step Guide to Problem Solving
Breaking down complex problems into manageable steps is a key skill in mathematics. By following a clear process, you can ensure that you address each part of the problem systematically, reducing the likelihood of errors. The process allows you to stay organized and focused, making it easier to find solutions and understand the reasoning behind them.
The following step-by-step approach is designed to guide you through solving various types of problems. By applying these steps consistently, you’ll improve your problem-solving skills and develop a deeper understanding of mathematical concepts.
| Step | Action | Description |
|---|---|---|
| 1 | Understand the Problem | Read the problem carefully and identify what is being asked. Make sure you know the key elements involved (such as the variable or the equation). |
| 2 | Identify Known and Unknown Values | List out the values that are given and identify the unknowns that need to be solved. This step helps you focus on what you need to find. |
| 3 | Choose a Strategy | Decide the best approach to solve the problem, whether it’s simplifying an equation, using substitution, or applying a specific formula. |
| 4 | Perform the Operations | Carry out the necessary mathematical operations step by step. Ensure that each operation is performed correctly before moving to the next. |
| 5 | Check Your Work | After solving the problem, review your steps to make sure no errors were made. Double-check calculations and make sure the solution makes sense in the context of the problem. |
By following this structured process, you will approach each problem with a clear strategy and ensure that your solutions are accurate and logical.
Tips for Efficient Exam Preparation
Preparing for a test requires more than just reviewing material–it’s about using your time wisely and focusing on the most effective strategies. By planning ahead and practicing regularly, you can improve your understanding and retention of key concepts. These tips will help you study smarter, not harder, and boost your confidence before the test.
Here are some practical strategies to help you prepare efficiently:
- Create a study schedule: Plan your study sessions in advance, breaking down the material into manageable sections. Allocate time for each topic, and be sure to include breaks to avoid burnout.
- Focus on weak areas: Identify the topics you find most challenging and spend extra time on them. Strengthening these areas will improve your overall performance.
- Use active recall: Instead of just reading notes, test yourself on the material. Write out key formulas, solve practice problems, or explain concepts in your own words.
- Practice under timed conditions: Simulate the test environment by practicing with timed questions. This helps you become more comfortable with the time constraints and improves your pacing during the actual test.
- Stay organized: Keep your notes, assignments, and practice materials in order. A well-organized study area can help you focus and reduce distractions.
- Get enough rest: Make sure to get a good night’s sleep before the test. A rested mind functions better and is more alert during problem-solving.
By applying these tips, you’ll be able to prepare effectively and reduce stress as you approach your test. Consistency, focus, and smart planning are key to achieving success.
Using Online Resources for Algebra Help
The internet offers a wealth of resources that can support your studies and help you understand challenging concepts. With the right tools, you can access tutorials, practice problems, and even personalized assistance to strengthen your skills. Online platforms provide flexibility, allowing you to learn at your own pace and revisit difficult topics as needed.
Whether you’re looking for detailed explanations, video lessons, or interactive exercises, there are numerous ways to supplement your learning and improve your understanding. Here are some of the best ways to use online resources for academic success:
Interactive Websites and Tutorials
Many websites provide step-by-step guides and practice problems to help reinforce concepts. These platforms often feature interactive elements, such as quizzes and flashcards, that allow you to test your knowledge and track your progress. Websites like Khan Academy and IXL are great examples of tools that cater to various levels of understanding and learning styles.
Online Forums and Study Groups
Online communities, such as forums and discussion groups, can also be valuable. Platforms like Reddit, Stack Exchange, or subject-specific forums provide a space where students can ask questions and get answers from peers or experts. Engaging in these communities allows you to share knowledge, learn from others, and clarify any doubts you may have.
By using these online resources, you can complement your traditional studies, gain deeper insights, and improve your problem-solving skills. With a variety of tools at your disposal, you can approach challenging subjects with confidence and success.
How to Check Your Answers Effectively
Reviewing your work is an essential step in ensuring accuracy and strengthening your understanding. Checking your solutions helps identify mistakes and ensures you’ve followed the correct process. By implementing effective strategies, you can improve the quality of your work and boost your confidence in problem-solving.
Here are several techniques to help you verify your results efficiently:
- Work Backwards: One of the most reliable methods is to reverse the steps of your solution. Start with your final result and work back towards the initial problem to see if everything checks out.
- Use Multiple Methods: If possible, try solving the same problem using different approaches. For example, if you solved an equation, check the solution by substituting it into the original problem to see if both sides are equal.
- Double-Check Each Step: Sometimes, errors occur during individual steps. Go through each part of your solution methodically, confirming that every calculation or decision was correct.
- Estimate the Result: Before diving into the details, estimate a reasonable answer. If your final result is drastically different from your estimate, it may be time to review the work.
- Use Technology: Many online tools and calculators can help confirm your results. For problems involving calculations, using a calculator or math app can act as a secondary check for accuracy.
By systematically reviewing your solutions, you can identify and correct errors more easily. Checking your work not only improves your chances of success but also deepens your understanding of the material.
| Method | Benefit |
|---|---|
| Work Backwards | Ensures the final result matches the original equation or condition. |
| Multiple Methods | Provides different perspectives to verify the solution. |
| Double-Check Each Step | Prevents minor errors from affecting the overall solution. |
| Estimate the Result | Helps identify any obvious errors based on expectations. |
| Use Technology | Provides an additional layer of verification for complex calculations. |
Test-Taking Strategies for Algebra Exams
Success in a written assessment relies not only on understanding the material but also on how you approach the test itself. Employing effective strategies during the test can help you manage time, reduce anxiety, and ensure a more accurate demonstration of your skills. By following certain techniques, you can navigate through problems more efficiently and boost your overall performance.
Effective Time Management
Time management is crucial in ensuring that you complete all sections of the assessment while maintaining accuracy. Here are some helpful strategies:
- Preview the Entire Test: Before you begin, quickly glance through all the questions to get an overview of the difficulty level and the time required for each. This can help you plan accordingly.
- Allocate Time for Each Section: Based on the number of questions and their complexity, allocate a specific amount of time for each section. Stick to this schedule as closely as possible.
- Don’t Get Stuck: If you find yourself spending too much time on a challenging question, move on to the next one. Return to difficult questions later if time permits.
Maximizing Your Focus and Performance
Staying focused throughout the test will help you avoid careless errors and ensure you approach each problem methodically. These techniques can help:
- Read Each Question Carefully: Before attempting a solution, read the question multiple times to ensure you fully understand what is being asked.
- Highlight Key Information: Underline or highlight important numbers or variables in the question that are critical to solving the problem.
- Work Systematically: Break down each problem into smaller steps and solve one part at a time. This reduces the chance of errors and allows you to stay organized.
- Double-Check Your Work: If time allows, go back over your answers to check for any errors or missed steps.
By using these strategies, you can enhance your test performance, increase your confidence, and improve your chances of achieving a higher score.
Understanding Word Problems in Algebra
Word problems are a common challenge for many students. They require translating real-world situations into mathematical expressions or equations. Understanding how to approach and break down these problems is key to solving them correctly. With the right strategies, you can turn complex scenarios into solvable tasks.
To solve word problems efficiently, it’s important to follow a systematic approach. Here are some essential steps to consider:
- Read the Problem Carefully: Take your time to read the problem at least twice. Make sure you understand the context and what is being asked.
- Identify Key Information: Highlight or underline important numbers, conditions, or relationships. This could include quantities, rates, or specific instructions on how to proceed.
- Define Variables: Choose a variable to represent the unknown quantity. This helps organize the information and allows you to translate the words into a mathematical equation.
- Set Up an Equation: Translate the relationships described in the problem into an equation. Use the variables to represent the unknowns, and make sure all the terms are accounted for.
- Solve the Equation: Once the equation is set up, use the appropriate methods to solve for the unknown variable(s).
- Interpret the Solution: Once you find the solution, make sure it answers the original question. Double-check that the answer makes sense within the context of the problem.
By following these steps, you can approach word problems with confidence and clarity. Practice is essential, so work through as many problems as possible to build your skills and improve your ability to identify the key elements needed for solving any situation.
How to Improve Your Algebra Skills
Improving your mathematical skills is a process that requires consistent effort and practice. Whether you’re struggling with basic concepts or looking to refine your abilities, there are several strategies you can employ to enhance your understanding and performance. The key to mastering these skills lies in practice, problem-solving, and applying what you learn in real-world situations.
Practice Regularly
One of the most effective ways to improve is through consistent practice. Work through problems daily to reinforce your knowledge and gain fluency. The more problems you solve, the better you’ll become at recognizing patterns and applying the correct methods. Start with simple exercises to build a strong foundation, then gradually move to more complex ones.
Seek Help When Needed
If you encounter difficulties, don’t hesitate to seek help. Whether it’s a teacher, tutor, or online resource, getting guidance can make a significant difference. Explaining problems to others or discussing solutions can also reinforce your understanding. Collaborating with others allows you to gain new perspectives and strengthen your grasp on difficult concepts.
By focusing on regular practice, seeking assistance when necessary, and applying what you learn, you can significantly improve your mathematical abilities. Stay persistent, and over time, you will see measurable progress in your performance and confidence.
Reviewing Key Formulas for Algebra 1
In any mathematical field, formulas serve as the backbone for solving problems and understanding core concepts. Mastery of essential formulas allows for quicker and more accurate problem-solving. This section will highlight the key formulas that are vital for mastering foundational concepts in math. Reviewing and memorizing these formulas can greatly improve your efficiency and confidence when solving problems.
Important Formulas to Remember
Here are some of the most commonly used formulas that form the basis of solving various types of problems. Familiarity with these formulas is crucial for tackling different exercises effectively.
| Formula | Description |
|---|---|
| Linear Equation: y = mx + b | This formula represents the slope-intercept form of a straight line, where “m” is the slope and “b” is the y-intercept. |
| Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a | This formula is used to find the solutions for quadratic equations of the form ax² + bx + c = 0. |
| Distance Formula: d = √((x₂ – x₁)² + (y₂ – y₁)²) | Used to calculate the distance between two points in a coordinate plane. |
How to Use These Formulas Effectively
To effectively use these formulas, it’s important to understand the context in which each formula is applied. Practice problems that involve these formulas can help you develop a deeper understanding of their usage. Additionally, recognizing the form of a problem will allow you to choose the appropriate formula to apply. Constant practice will improve your ability to recall and apply these formulas quickly and correctly.
How to Overcome Algebra Exam Anxiety
Feeling anxious before a test is a common experience for many students, especially when facing complex problems or time constraints. The pressure to perform well can create stress, which may hinder your ability to think clearly and apply what you’ve learned. It’s important to recognize that anxiety can be managed and that with the right strategies, you can approach any challenge with confidence. This section provides tips on how to reduce stress and overcome anxiety during math assessments.
Preparation is Key
One of the most effective ways to reduce exam-related anxiety is thorough preparation. When you feel confident in your understanding of the material, anxiety naturally decreases. To prepare effectively:
- Practice regularly: The more problems you solve, the more comfortable you become with various types of questions.
- Review key concepts: Focus on the most important topics and formulas to ensure you are fully prepared for any type of problem.
- Use study guides: Follow a structured study plan to cover all the necessary material, which will help you avoid last-minute cramming.
Mindfulness and Relaxation Techniques
Managing anxiety isn’t just about preparing academically–it’s also about preparing mentally and emotionally. Here are a few techniques to help you relax and stay focused:
- Practice deep breathing: Take a few deep breaths before the test and during moments of anxiety to calm your nerves.
- Visualization: Imagine yourself successfully solving problems and staying calm during the assessment.
- Positive self-talk: Remind yourself that you are prepared and capable of doing well.
By combining solid preparation with mental relaxation techniques, you can significantly reduce anxiety and improve your performance on assessments.