Algebra 1 Regents Exam Random Questions and Answers Worksheet

Studying for a standardized assessment involves more than just memorizing formulas or concepts. It requires developing a deep understanding of various mathematical principles and applying them to solve diverse problems. One effective way to reinforce your skills is through engaging with a variety of practice exercises that test your ability to think critically and logically under pressure.
These exercises are designed to simulate the types of challenges you might encounter, helping you familiarize yourself with different problem structures. By regularly working through various scenarios, you can identify patterns, improve your problem-solving techniques, and build the confidence needed to tackle any type of mathematical challenge.
Reviewing solutions after completing each set of exercises is just as important as practicing. It provides an opportunity to understand any mistakes made and refine your approach. In this way, every practice session becomes a valuable learning experience, offering insights that can lead to better performance when it matters most.
Algebra 1 Regents Exam Random Questions
When preparing for a major assessment, exposure to a wide range of problems is key. This approach ensures familiarity with different types of challenges and reinforces essential skills. By engaging with diverse problem sets, you can enhance your ability to tackle a variety of scenarios, building both confidence and competence in your mathematical abilities.
Incorporating a mix of exercises simulating potential real-world and academic problems allows you to master core concepts in an applied context. This method encourages critical thinking and flexibility, helping you adapt quickly to unfamiliar formats or unexpected question styles. Regular practice with such material is one of the most effective strategies for ensuring success under exam conditions.
Furthermore, working through these varied tasks helps pinpoint areas that need improvement, making it easier to focus your study efforts. Identifying common patterns across problems provides insight into the reasoning required to solve them effectively, helping you sharpen your overall approach.
Understanding Algebra 1 Exam Format
Familiarity with the structure of a major assessment is crucial for effective preparation. Knowing the format allows students to anticipate the types of tasks they will encounter, manage their time effectively, and reduce anxiety during the actual test. Understanding the layout ensures that you can focus on applying the right strategies to each section without being caught off guard by unexpected formats.
The test typically consists of multiple sections, each designed to assess different skills and areas of knowledge. Some sections may include multiple-choice items, while others require detailed problem-solving. The balance between these types of questions is meant to test both basic understanding and the ability to apply concepts to complex situations. Being able to navigate these various formats is a key aspect of preparation.
In addition to knowing the structure, it’s important to become accustomed to the time constraints associated with the assessment. Practicing under timed conditions will help you develop pacing strategies to ensure that each problem is given the appropriate amount of attention. With the right preparation and an understanding of the test’s design, you can approach the assessment with confidence.
How Randomized Questions Help Exam Preparation
Introducing a variety of unpredictable challenges into study routines plays a crucial role in preparing for an assessment. By practicing with exercises that change in format or order, students can strengthen their problem-solving abilities and ensure they are ready for any scenario that may arise on test day. This approach helps to simulate the dynamic nature of the actual test environment, reducing the likelihood of being caught off guard.
Benefits of Practice with Varied Tasks
- Improved adaptability to different problem formats.
- Enhanced ability to recognize patterns and solve problems efficiently.
- Boosted confidence when faced with unexpected challenges.
Fostering Critical Thinking and Flexibility

When exercises are presented in an unpredictable order, students are forced to think critically and adapt their methods to each unique situation. This builds mental flexibility, which is essential for approaching complex problems with different structures. By continuously engaging with diverse content, learners are better equipped to apply their knowledge in a wide range of contexts.
Key Concepts Covered in Algebra 1
The foundation of many mathematical assessments lies in mastering a set of core principles. These concepts are designed to assess one’s ability to think logically and apply mathematical reasoning to solve problems. Understanding these fundamental topics is essential for achieving success in any academic challenge that involves mathematical concepts and calculations.
Some of the critical ideas explored include:
- Understanding and manipulating linear relationships.
- Working with equations and inequalities.
- Graphing and interpreting functions.
- Exploring systems of equations and their solutions.
- Factoring expressions and solving quadratic equations.
By focusing on these key areas, students build a solid foundation for solving more advanced problems. Each concept plays a vital role in strengthening analytical skills and fostering a deeper understanding of mathematical structures.
Effective Strategies for Answering Questions
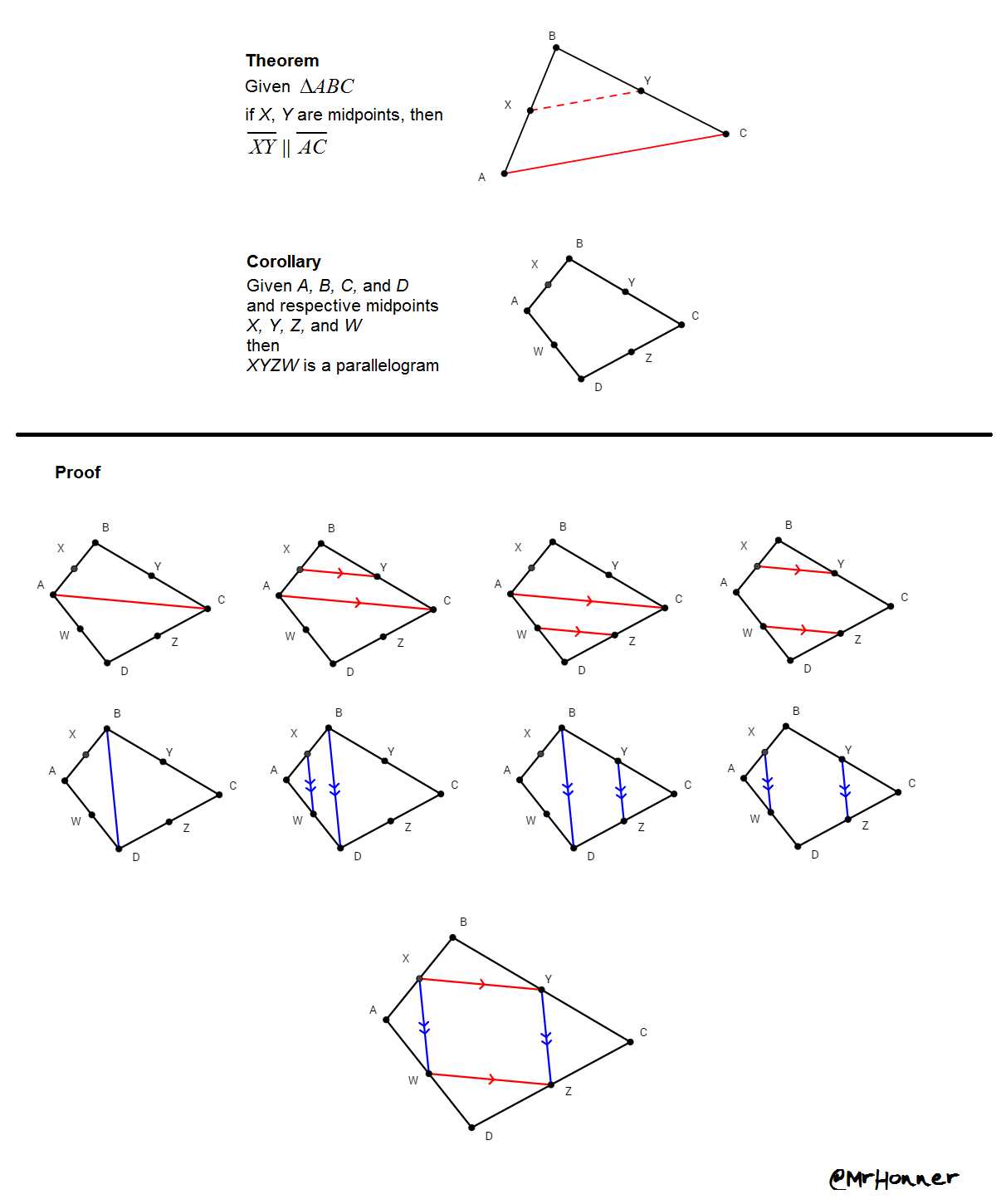
Approaching problems efficiently requires a thoughtful strategy that allows you to tackle each challenge methodically. Developing effective techniques for solving tasks not only helps you save time but also improves the accuracy of your responses. By adopting structured methods, you can confidently navigate through even the most complex problems.
Key Strategies to Consider
- Read the problem carefully to ensure full understanding before starting.
- Break down complex tasks into smaller, manageable steps.
- Eliminate clearly incorrect options when faced with multiple choices.
- Use estimation to check the reasonableness of your answers.
Improving Problem-Solving Efficiency
- Prioritize problems based on difficulty and time constraints.
- Use visualization tools like graphs or diagrams to simplify calculations.
- Double-check calculations and solutions to avoid simple mistakes.
By integrating these strategies, you will improve both your speed and accuracy, making the process of solving each task much more efficient.
Importance of Practice Worksheets in Studying
Regularly working through practice exercises is a key element of successful study routines. These activities not only help reinforce previously learned concepts but also offer opportunities to apply knowledge in various contexts. The consistent engagement with problems is essential for strengthening understanding and improving problem-solving skills.
Benefits of Practice Exercises
- Reinforces key concepts by applying them in different scenarios.
- Helps identify areas that need improvement and focus.
- Develops critical thinking skills by challenging the mind to solve diverse problems.
Enhancing Retention and Confidence
- Regular practice leads to better retention of information over time.
- Building confidence in tackling problems, especially under pressure.
- Improves speed and accuracy, making it easier to handle timed assessments.
By incorporating these exercises into your routine, you can build a solid foundation of knowledge and develop the skills needed to perform well in any testing situation.
Common Mistakes to Avoid During the Exam
During any important assessment, it’s easy to make errors that could impact your performance. These mistakes often arise from lack of preparation or simple lapses in focus, but they can be easily avoided with careful attention and a strategic approach. Recognizing the common pitfalls and taking steps to avoid them can significantly improve your results.
Typical Errors to Watch Out For
- Rushing through questions without fully reading or understanding them.
- Forgetting to review calculations or assumptions before finalizing answers.
- Misinterpreting the wording of a problem, leading to incorrect assumptions.
- Spending too much time on a single problem and neglecting others.
Strategies for Avoiding Mistakes

- Double-check your work, especially for simple arithmetic or calculation errors.
- Use the process of elimination for multiple-choice items to narrow down options.
- Stay mindful of time and pace yourself to avoid rushing through the test.
- Ensure you’re clear on the requirements of each task before starting.
By being aware of these common mistakes and employing effective strategies, you can navigate the test with greater confidence and accuracy, ultimately improving your performance.
How to Improve Problem-Solving Skills
Mastering problem-solving is a vital skill that extends beyond academic assessments. The ability to approach challenges logically and systematically can make a significant difference in performance and understanding. By refining problem-solving techniques, you can develop stronger analytical abilities and boost your confidence when tackling complex tasks.
Effective Strategies for Enhancement
- Break problems down into smaller, more manageable steps.
- Identify patterns and relationships between different elements of the problem.
- Consider multiple approaches to solve a problem before settling on one solution.
- Stay organized by keeping track of your thought process and solutions.
Building Mental Agility
- Practice regularly with a variety of problems to increase your flexibility.
- Challenge yourself with more difficult tasks to push your limits.
- Review and reflect on your solutions to understand what worked and why.
By adopting these strategies, you’ll gradually build a toolkit of methods and approaches that will help you solve problems more effectively, enhancing both your skills and your success in future challenges.
Using Timed Practice for Better Results
Incorporating time constraints into your study routine is an effective way to improve both speed and accuracy. By simulating time-limited conditions, you can better prepare yourself for the pressure of real assessments. Timed practice not only helps build a sense of urgency but also enhances your ability to make quick, well-thought-out decisions under pressure.
Advantages of Timed Practice

- Improves time management skills, ensuring you complete tasks within a set period.
- Reduces anxiety by familiarizing yourself with time constraints before the real test.
- Increases focus and concentration, helping you avoid distractions.
Tips for Effective Timed Practice
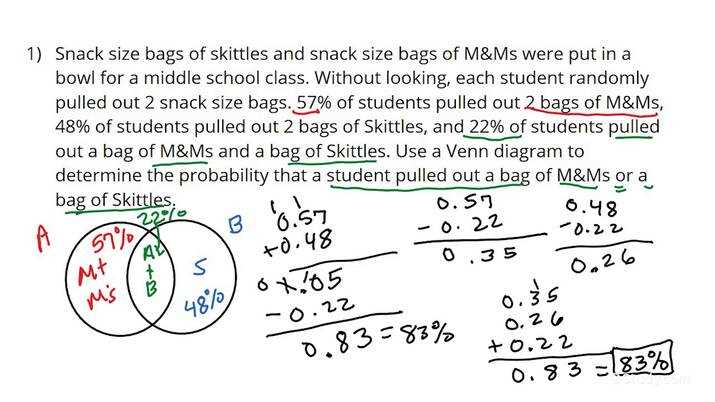
- Start with manageable time limits and gradually decrease them as you improve.
- Track your progress and aim to complete each task more efficiently over time.
- Review your performance after each practice session to identify areas for improvement.
By regularly practicing under timed conditions, you can strengthen your ability to stay calm and efficient, ensuring better results when it matters most.
Benefits of Reviewing Worksheet Answers
Reviewing completed tasks is an essential step in the learning process, as it provides an opportunity to reflect on your work and identify areas of improvement. By carefully checking your responses, you can recognize mistakes, reinforce your understanding, and solidify concepts that might need more practice. This process is crucial for long-term retention and skill development.
Key Benefits of Revisiting Your Work
- Helps identify common errors and understand why they occurred.
- Improves your ability to recognize patterns in problem-solving approaches.
- Enhances retention by reinforcing correct methods and solutions.
How Review Contributes to Improvement
- Revisiting tasks boosts confidence by ensuring you’re on the right track.
- Increases efficiency by allowing you to learn from mistakes and avoid repeating them.
- Offers insights into the areas that need more focus in future study sessions.
By dedicating time to thoroughly reviewing your work, you can strengthen your skills, minimize errors, and improve your overall performance in future tasks.
Real-Life Applications of Algebra 1 Concepts
The concepts learned in introductory mathematics are more than just abstract ideas–they have practical applications in everyday life. Understanding how to work with variables, equations, and functions equips you with tools that can help solve real-world problems, whether you’re budgeting, analyzing trends, or designing projects. These skills are not only useful in academic settings but are also essential in many professional fields.
Practical Uses in Daily Life

- Personal finance: Calculating savings, budgeting, and understanding loan interest.
- Shopping: Determining discounts, taxes, and comparing prices for better deals.
- Technology: Programming algorithms, working with data analysis, and creating software applications.
Applications in Various Fields
| Field | Example |
|---|---|
| Engineering | Designing structures and solving for unknowns in measurements. |
| Healthcare | Understanding dosage calculations, medical statistics, and growth rates of diseases. |
| Business | Analyzing profit margins, calculating production costs, and forecasting sales trends. |
Mastering these foundational principles can open doors to numerous opportunities, providing the ability to approach challenges with logic and precision. By applying these concepts in various situations, you build a stronger, more versatile skill set that is highly valued in both personal and professional contexts.
Tips for Tackling Multiple Choice Questions
When faced with multiple-choice challenges, having a solid strategy can make a significant difference in performance. These types of questions often present a set of options, requiring careful thought to select the correct one. By approaching them systematically, you can increase your chances of choosing the right answer, even when unsure.
Effective Strategies for Success

- Read Carefully: Always read the entire question and all answer options before selecting your choice.
- Eliminate Wrong Choices: Cross out any options that are clearly incorrect to narrow down your choices.
- Look for Clues: Sometimes, words in the question can hint at the correct answer or help you rule out others.
- Guess Strategically: If you’re unsure, make an educated guess based on what you know. Choose the most logical answer based on your understanding.
Additional Tips to Keep in Mind
- Don’t Rush: Take your time to think through each question carefully. Avoid guessing hastily, as this may lead to mistakes.
- Check for Keywords: Pay attention to qualifiers like “always,” “never,” or “most likely,” which can affect the answer’s validity.
- Stay Calm: Maintain composure, especially when you encounter difficult questions. Stress can cloud judgment and lead to errors.
With practice and these strategies in mind, you can approach multiple-choice questions with confidence, ensuring that you’re selecting the best possible answer every time.
How to Interpret Question Phrasing
Understanding the way a problem is worded is essential for finding the correct solution. The phrasing of a problem can provide vital clues that help you identify the required steps to solve it. Whether it’s the use of specific terminology or the structure of the sentence, being able to decode the language of a problem ensures you don’t miss key information.
Key Phrasing Techniques
- Look for Action Words: Words like “calculate,” “determine,” or “evaluate” signal what you need to do. Identifying the action required helps you stay focused on the main objective.
- Pay Attention to Details: Words such as “each,” “total,” or “difference” indicate specific calculations. Noticing these can guide you toward the correct operation.
- Identify Special Terms: Be aware of terms like “maximum,” “minimum,” or “average,” which provide context for the type of answer expected.
Common Phrasing Pitfalls
- Multiple Conditions: When a problem includes several conditions or requirements, ensure you address each one separately and correctly.
- Negatives and Double Negatives: Watch for words like “not,” “never,” or “except.” These can alter the direction of your solution, so read carefully to avoid mistakes.
- Inclusive vs. Exclusive Language: Pay attention to whether the problem asks for a “range” or a “specific value,” as these can change how you approach the solution.
By practicing the interpretation of different phrasings, you’ll develop a better understanding of what is being asked. With time and attention, you can master the art of recognizing key clues in problem statements, ensuring that you’re always on the right track.
Maximizing Your Time on Test Day
Effective time management on the day of a test can significantly improve your performance. Being able to allocate your time wisely ensures that you can complete all sections, review your work, and avoid rushing. With proper planning and strategy, you can make the most out of the limited time available to you.
One key strategy is to quickly assess the layout of the test. By scanning through the questions and their point values at the start, you can prioritize which ones to tackle first. In some cases, focusing on questions that you are most confident in will help build momentum and reduce stress. At the same time, it’s important to not spend too much time on any single question.
Time Allocation Strategy
| Section | Recommended Time | Tips |
|---|---|---|
| Initial Review | 5-10 minutes | Scan all questions to get an overview and mark easier questions to tackle first. |
| High-Priority Questions | 40-50 minutes | Start with questions you’re most confident in to ensure you collect easy points. |
| Challenging Questions | 20-30 minutes | Spend focused time on difficult questions but avoid getting stuck. Move on if necessary. |
| Review and Final Checks | 10-15 minutes | Check for errors, especially in calculations or wordings, and ensure all questions are answered. |
In addition, staying aware of the time as you progress through the test is crucial. Use a watch or clock to keep track, but don’t obsess over it. By following a structured approach, you can approach each part of the test with confidence and maximize your potential for success.
Commonly Tested Topics in Algebra 1
Throughout the course of your studies, there are several key areas that are consistently evaluated. Mastery of these concepts is crucial for achieving success. Understanding these topics not only helps in tackling specific problems but also builds a strong foundation for future mathematical learning.
Focus on areas that involve manipulating expressions, solving equations, and understanding relationships between variables. These fundamental topics are often the cornerstone of the subject and are repeatedly tested, whether through direct problem-solving or conceptual analysis. Below are some of the most important areas to prioritize during your preparation.
Key Areas of Focus
- Linear Equations and Inequalities: Knowing how to solve, graph, and interpret the meaning of linear equations is essential.
- Systems of Equations: Be prepared to solve systems using various methods, including substitution and elimination.
- Polynomials: Simplifying, factoring, and expanding polynomials are key skills for problem-solving.
- Quadratic Functions: Understanding the properties of quadratic equations and their graphs is critical for success.
Conceptual Mastery
- Exponents and Powers: Proficiency with laws of exponents and their applications is essential in simplifying expressions.
- Rational Expressions: Knowing how to simplify and solve problems involving fractions with variables will be tested frequently.
- Radicals: Simplifying expressions with square roots and higher-order roots is a commonly tested skill.
- Functions and Relations: Understanding the concept of functions, domain, and range will help you solve many types of problems.
Focusing on these areas will not only help you perform well but will also improve your ability to approach new and unfamiliar problems with confidence. Practice is the key to success, and mastering these topics will lay the groundwork for tackling more advanced subjects in mathematics.
Preparing for the Algebra 1 Regents Exam
Effective preparation is essential for success in any formal assessment. To perform well, it is important to focus on strengthening your understanding of key concepts and practicing regularly. By reviewing important topics and refining problem-solving skills, you can approach the test with confidence and achieve your best results.
When preparing, consider organizing your study time to cover all major areas and test formats. It’s also helpful to incorporate timed practice sessions, as this can simulate the actual testing environment and help you manage time effectively. Below are some strategies that can enhance your readiness and boost your performance.
Effective Study Techniques
- Review Core Concepts: Focus on the fundamental principles that are frequently tested. These may include solving linear equations, working with exponents, and graphing functions.
- Practice with Sample Problems: Regular practice with a variety of problems will help you identify common patterns and improve your ability to solve unfamiliar problems.
- Use Study Guides: Take advantage of study materials that summarize key points and provide practice problems with explanations.
Time Management During Preparation
- Set a Study Schedule: Break down your study sessions into manageable blocks of time, focusing on one concept at a time.
- Take Breaks: Schedule short breaks during study sessions to maintain focus and avoid burnout.
- Simulate Testing Conditions: Practice solving problems under timed conditions to build speed and efficiency.
With diligent preparation and consistent practice, you can build the confidence and skills needed to excel. Additionally, it is important to approach the assessment with a clear mind and a positive attitude. By following these strategies and reviewing key topics, you will be well-prepared for success.
Resources for Further Algebra 1 Practice
To deepen your understanding and refine your problem-solving skills, it is crucial to make use of a variety of study materials and resources. These tools can provide valuable practice, explanations, and strategies to enhance your learning. Whether you are seeking online platforms, textbooks, or interactive simulations, numerous options are available to help you master key concepts and improve your ability to tackle complex problems.
Here are some recommended resources for extra practice that can supplement your study routine:
Online Platforms
- Khan Academy: Offers free instructional videos, practice exercises, and personalized learning dashboards to help students master various topics.
- IXL: Provides comprehensive practice problems and immediate feedback to help improve performance on specific skills.
- Brilliant: Features interactive lessons and problem sets, focusing on building strong problem-solving abilities.
Textbooks and Study Guides
- The Princeton Review: Includes detailed explanations and practice tests to reinforce key concepts and improve your test-taking strategies.
- McGraw-Hill Education: Offers a variety of workbooks and study guides with both practice exercises and step-by-step solutions for self-guided learning.
- Barron’s: A trusted name in test prep, offering resources with practice questions and clear explanations.
Interactive Tools
- Desmos: An online graphing calculator that helps visualize functions, equations, and inequalities, making it easier to understand abstract concepts.
- GeoGebra: A dynamic mathematics software platform that provides interactive tools for algebra and geometry practice.
By utilizing these resources, you can reinforce your skills, gain confidence, and improve your ability to solve a wide range of problems. Incorporating different types of practice will give you a well-rounded preparation strategy and increase your chances of success.