Geometry Regents Answers and Solutions Guide

Success in mathematical assessments requires more than just basic knowledge; it demands understanding, practice, and effective problem-solving strategies. Students often face challenges when tackling complex problems, but with the right approach, these obstacles can be easily overcome.

In this section, we’ll delve into effective methods for solving problems commonly found in exams. From mastering essential formulas to understanding logical reasoning techniques, you’ll gain insights that can help boost your confidence and performance. Whether you’re preparing for your first test or looking to improve your score, this guide will provide valuable tips and resources.

By focusing on practice and understanding key concepts, you’ll be better equipped to tackle any problem, ensuring that you’re well-prepared for success in your upcoming evaluations. Efficient preparation is the ultimate key to feeling ready when the time comes to showcase your skills.

Mathematical Assessment Overview

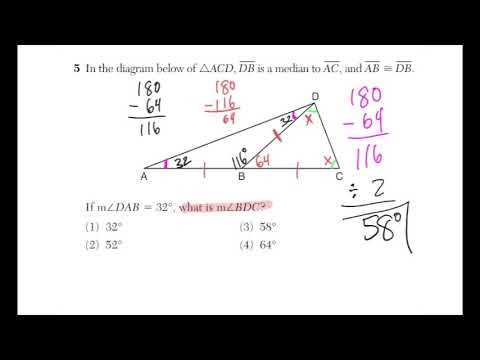
The upcoming assessment in mathematics is designed to evaluate your understanding and problem-solving abilities across a variety of topics. This comprehensive test challenges students with a wide range of questions that assess not only their knowledge but also their logical reasoning and analytical skills.

The examination consists of several sections, each focusing on different aspects of mathematical concepts. It includes multiple-choice questions, open-ended problems, and reasoning tasks that require careful thought and application of learned principles. Success on this test depends on the ability to approach each question with clarity and precision, using the right techniques to solve problems efficiently.

By familiarizing yourself with the format and structure of the test, you can better plan your preparation and reduce any anxiety. Thorough practice and understanding of the core mathematical principles will help you navigate through the questions with confidence, ensuring that you can perform at your best.

Key Topics Covered in Mathematical Assessments

This examination evaluates a wide range of concepts in mathematics, testing your ability to apply foundational principles and solve complex problems. Topics include essential aspects such as properties of shapes, measurements, transformations, and logical reasoning techniques. Mastery of these subjects is critical for achieving high marks on the test.

Specific areas of focus include understanding the relationships between different types of figures, theorems about angles, lines, and polygons, as well as the ability to calculate areas, volumes, and other important metrics. You will also encounter problems that require spatial reasoning and the application of algebraic methods in geometric contexts.

By familiarizing yourself with these key topics, you can develop a stronger foundation in the core areas of mathematics that will be tested. Practice and review of these concepts will prepare you for a range of question types, from straightforward calculations to more complex, multi-step reasoning tasks.

How to Prepare for the Mathematical Assessment

Effective preparation for any math exam requires a well-structured approach. It’s important to review key concepts, practice regularly, and develop problem-solving strategies that will help you navigate through various question types. Understanding the format and the specific requirements of the test is the first step towards ensuring a successful outcome.

Understand the Test Format

Familiarizing yourself with the structure of the exam can give you a significant advantage. Know how many sections the test has, the types of questions you will encounter, and the time limits for each section. This will allow you to plan your time wisely and avoid rushing through complex problems.

Practice with Sample Problems

Working through practice questions is one of the best ways to reinforce your knowledge and identify areas that need improvement. Focus on solving a variety of problems, from basic calculations to more intricate reasoning tasks. The more you practice, the more confident you will become in applying different techniques and strategies during the actual exam.

Tips for Solving Mathematical Problems

Solving mathematical challenges effectively requires a combination of strategy, practice, and critical thinking. By mastering certain techniques and approaches, you can tackle even the most complex problems with confidence. Whether you’re working through basic calculations or intricate proofs, these tips will help you stay focused and organized.

Break Down the Problem

When faced with a challenging question, take the time to read it carefully and break it down into smaller, more manageable steps. Identify the key information provided and what is being asked. This will help you organize your thoughts and prevent feeling overwhelmed by the complexity of the task.

Use Visual Aids and Diagrams

Whenever possible, draw diagrams or create visual representations of the problem. Diagrams can often reveal relationships between elements that are not immediately obvious in the written description. Labeling important parts of the diagram, such as angles or lengths, can guide you in applying the correct formulas and methods.

Common Mistakes on Mathematical Assessments

Many students encounter similar challenges when tackling mathematical exams, often due to avoidable mistakes. These errors typically arise from misunderstandings of concepts, rushed calculations, or misinterpretations of questions. Recognizing and addressing these common pitfalls can greatly improve performance on the test.

Common Mistakes to Avoid

• Skipping key steps in problem-solving, leading to incomplete or incorrect solutions.
• Misreading questions, especially those that require multiple steps or involve tricky wording.
• Forgetting to check the units of measurement or converting them incorrectly.
• Relying on memorized formulas without fully understanding when or how to apply them.
• Not drawing diagrams or visualizing the problem, which can make relationships between elements unclear.

How to Minimize These Errors

1. Always read the problem thoroughly and underline or highlight key information.
2. Double-check calculations and solutions to ensure every step aligns with the correct method.
3. Use diagrams and visual aids to help with spatial understanding and calculations.
4. Practice time management to avoid rushing through questions in the final moments.
5. Review common formulas and ensure you understand how they relate to the problem at hand.

Understanding Mathematical Theorems and Postulates

A solid grasp of key theorems and postulates is essential for solving many mathematical problems. These fundamental principles provide the logical foundation for many proofs and problem-solving strategies. Understanding when and how to apply them can greatly improve your ability to work through complex questions.

Key Theorems and Postulates to Remember

• Parallel Postulate: If a line is parallel to one of two intersecting lines, it will be parallel to the other as well.
• Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
• Angle Sum Theorem: The sum of the interior angles of any triangle is always 180°.
• Congruence Postulate: If two triangles have the same size and shape, their corresponding sides and angles are congruent.
• Vertical Angles Theorem: Opposite angles formed by two intersecting lines are always equal.

How to Apply Theorems and Postulates Effectively

1. Memorize the most commonly used theorems and postulates so that you can quickly recall them during problem-solving.
2. Understand the proof behind each principle to ensure you can apply them correctly in various contexts.
3. Use diagrams to visually represent the relationships between elements and better understand how to apply these principles.
4. Practice solving problems using the theorems and postulates to gain confidence in your ability to apply them accurately.

Practice Questions for Mathematical Assessments

Regular practice with sample questions is one of the most effective ways to prepare for any math exam. By solving a variety of problems, you can improve your problem-solving skills, familiarize yourself with the exam format, and strengthen your understanding of key concepts. Below are a few sample problems that will help you test your knowledge and apply the skills you’ve learned.

Question	Topic	Answer
Find the area of a triangle with a base of 8 cm and height of 5 cm.	Area Calculation	20 cm²
Calculate the length of the hypotenuse in a right triangle with legs of 6 cm and 8 cm.	Pythagorean Theorem	10 cm
Determine the measure of angle x if two parallel lines are cut by a transversal and one angle is 120°.	Angle Relationships	60°
Find the volume of a rectangular prism with length 4 cm, width 3 cm, and height 5 cm.	Volume Calculation	60 cm³
What is the perimeter of a square with a side length of 7 cm?	Perimeter Calculation	28 cm

Reviewing Mathematical Solution Keys

Reviewing solution keys is a crucial step in preparing for any math examination. By going over the correct solutions to problems, students can identify areas where they may have made mistakes and learn from those errors. Analyzing the steps involved in arriving at the right answer helps solidify understanding and improve future problem-solving abilities.

Why Reviewing Solution Keys is Important

• Identifies Mistakes: Going over the correct solutions allows you to pinpoint errors in your calculations or reasoning.
• Reinforces Concepts: Seeing the correct approach reinforces important mathematical principles that you might have missed or misunderstood.
• Builds Confidence: Understanding how to solve problems step-by-step boosts your confidence for future tests.
• Enhances Problem-Solving Skills: By examining how each problem is solved, you gain insight into effective problem-solving strategies.

How to Effectively Review Solution Keys

1. Compare your work to the provided solutions and look for discrepancies. Understand why a particular approach works.
2. Focus on the reasoning behind each step, not just the final answer. This will help you apply the same logic to new problems.
3. Review any mistakes and redo the problems using the correct methods. Practice will help you avoid repeating the same errors.
4. If there’s a step or concept you don’t understand, take time to revisit that topic with additional resources or guidance.

Time Management for Mathematical Assessments

Effective time management is key to performing well on any timed exam. Allocating enough time to each section of the test ensures that you don’t rush through important questions or leave any unanswered. With proper planning and preparation, you can approach the exam with confidence and complete it within the allotted time.

Strategies for Effective Time Management

One of the most effective ways to manage your time during an exam is by prioritizing the questions. Start by quickly scanning the entire test to identify easier problems that you can answer quickly. These initial questions will build your confidence and save valuable time for more challenging problems later. Aim to spend the appropriate amount of time on each section, and if a question is particularly difficult, don’t dwell on it too long. Move on and return to it if time permits.

Practice with Timed Tests

Familiarity with the exam format can significantly improve your time management skills. Practice solving sample problems under timed conditions to simulate the actual testing environment. This will help you gauge how much time to spend on each question, avoid common pitfalls, and develop a strategy that works best for you.

Scoring and Grading for Mathematical Assessments

Understanding how your performance is evaluated on a math exam is essential for setting goals and improving your approach to test-taking. The scoring process typically involves multiple components, including correct answers, logical reasoning, and the ability to apply concepts effectively. Each section is weighted differently, and knowing how the grading works can help you focus on areas that matter most.

Scoring Breakdown

Scores are usually divided into different categories, depending on the complexity of the questions and the skills being tested. Below is a general overview of how scoring is typically structured for math exams:

Section	Description	Weight
Multiple Choice	Test of basic concepts, quick problem-solving, and recall of formulas.	50%
Short Response	Questions that require step-by-step solutions and logical reasoning.	30%
Extended Response	In-depth problems where you explain your approach and demonstrate problem-solving strategies.	20%

Grading Scale

Once the exam is scored, results are assigned to a grading scale. This scale typically ranges from a passing score to a failing score, with intermediate levels to reflect proficiency and understanding. Here is a sample of a common grading scale used in math assessments:

Score Range	Grade
85-100%	Excellent
70-84%	Good
50-69%	Needs Improvement
Below 50%	Failing

Strategies for Multiple-Choice Questions

Multiple-choice questions are a common part of many exams, and knowing how to approach them can greatly improve your chances of success. The key to answering these questions effectively lies in understanding the question, analyzing the options carefully, and using strategic techniques to eliminate incorrect answers.

Effective Approaches for Tackling Multiple-Choice Questions

• Read the Question Thoroughly: Ensure you understand what is being asked before looking at the choices. Pay attention to keywords like “always,” “never,” “most,” or “least.”
• Eliminate Obvious Incorrect Answers: Cross out choices that are clearly wrong to narrow down your options.
• Use Logic and Reasoning: Analyze the question and use your knowledge to evaluate each answer. Sometimes, the correct choice may be the one that makes the most logical sense based on what you know.
• Don’t Rush: Take your time with each question, but also keep track of the time to ensure you can address all questions.
• Make Educated Guesses: If you’re unsure, eliminate one or two choices and make your best guess from the remaining options.

Common Pitfalls to Avoid

• Overthinking: Avoid over-analyzing questions. Trust your first instinct unless you can justify a change.
• Leaving Questions Blank: Never leave a question unanswered if there’s a chance to guess, especially if there’s no penalty for incorrect answers.
• Misinterpreting Negative Questions: Be careful with questions that use negative language, such as “Which of the following is NOT true?” Make sure to read them carefully.

Mathematical Exam: What to Expect

Understanding what to expect in a standardized math assessment can help alleviate any anxiety and improve your performance. These exams are designed to evaluate your comprehension of key concepts, problem-solving skills, and your ability to apply learned strategies to a variety of mathematical scenarios. The format typically consists of multiple-choice questions, short-answer problems, and extended-response sections that require more detailed explanations and solutions.

Types of Questions: You will encounter a mix of question types that assess different levels of understanding. The multiple-choice questions test your basic knowledge and quick reasoning abilities, while short-answer questions require you to show your work and reasoning. Extended-response questions, on the other hand, will challenge you to explain your thought process and solve complex problems step-by-step.

Time Constraints: Time management is crucial during the exam. It’s important to pace yourself, ensuring that you allocate enough time for each section, especially the more complex problems that may require extra thought and calculation. Prioritize sections you are most comfortable with to ensure you score high in those areas, then return to more challenging problems.

Resources for Math Exam Study

Preparing for a challenging mathematics exam requires access to a variety of study materials and resources. With the right tools, you can reinforce your understanding, practice key concepts, and refine problem-solving skills. These resources can help you identify your strengths and address any areas where improvement is needed.

Online Tools and Websites

• Interactive Practice Tests: Many websites offer free practice exams that mimic the format and difficulty of the real test. These allow you to familiarize yourself with the types of questions and test your speed and accuracy under timed conditions.
• Video Tutorials: Platforms like YouTube or educational websites provide video lessons that explain complex concepts in a more visual format. These can be extremely helpful for understanding geometric principles and seeing step-by-step problem-solving methods.
• Educational Forums: Online forums and communities can be invaluable for getting answers to specific questions or discussing difficult topics with peers and educators.

Books and Study Guides

• Review Books: Comprehensive study guides are available in bookstores or online. These books often include practice problems, past exam papers, and detailed explanations of various topics to help you prepare efficiently.
• Flashcards: Using flashcards for memorizing formulas, theorems, and key concepts can boost retention and speed. Many flashcard apps are available to help you study on the go.

How to Improve Your Math Skills

Mastering mathematical concepts requires consistent practice, focused learning, and a strong understanding of core principles. To enhance your problem-solving abilities and boost your performance, it’s important to approach your studies strategically. Strengthening these skills involves a combination of theory, hands-on practice, and review.

Build a Strong Foundation

The key to improving your abilities in mathematics lies in mastering the basics. Start by ensuring you have a clear understanding of fundamental concepts. For example, work through simple problems and gradually increase the complexity as you become more comfortable with each topic. Focus on concepts like angles, shapes, measurements, and basic calculations.

Practice Regularly

Consistent practice is essential for improving math skills. Solve different types of problems every day to keep your mind engaged. Use worksheets, online quizzes, and textbooks to find a variety of exercises that challenge your current level of understanding. The more problems you work through, the more confident you will become in applying mathematical techniques to new situations.

Math Exam Review Guide for Students

Preparing for a challenging math exam can feel overwhelming, but with a structured approach and the right resources, it becomes much more manageable. This guide is designed to help students systematically review key concepts and practice essential skills needed to succeed. By following a focused study plan, you can improve both your understanding and your confidence before test day.

Key Topics to Focus On

Start by identifying the core areas that are most frequently tested. These often include topics like problem-solving strategies, algebraic principles, spatial reasoning, and theorems. Review any class notes, textbooks, or online resources to ensure you have a solid understanding of these areas. Break them down into manageable sections and allocate time for each topic in your study schedule.

Effective Study Strategies

• Practice with Past Papers: Review previous exams to get a feel for the format and types of questions. This will help you identify patterns and focus your study on the areas that require the most attention.
• Group Study Sessions: Working with classmates can be a great way to tackle difficult problems and gain new perspectives. Discuss challenging concepts and quiz each other on key topics.
• Time Management: During your study sessions, time yourself to simulate real exam conditions. This helps build your ability to manage time effectively on the actual test day.

Final Checklist Before Math Exam

As the exam day approaches, it is essential to ensure that all preparation is in place. This checklist is designed to guide you through the final steps to make sure you’re fully ready. By focusing on the critical tasks and reviewing key concepts one last time, you can approach the test with confidence and clarity.

• Review Key Concepts: Go over the most important topics that are likely to appear on the exam. Refresh your memory on formulas, theorems, and essential problem-solving strategies.
• Practice Under Timed Conditions: Take a practice test or work through sample problems while keeping track of time. This will help you manage your time efficiently during the actual exam.
• Check Your Materials: Make sure you have all the necessary tools for the exam, such as pencils, erasers, a calculator (if allowed), and any other required materials.
• Get Enough Rest: A good night’s sleep before the exam is crucial. Rest well so you can be alert and focused on the test day.
• Stay Positive: Keep a positive mindset. Confidence can play a significant role in how you perform during the exam.