Algebra 1 Module 2 Answers and Solutions

In this section, we will explore the essential concepts and methods needed to solve various mathematical problems effectively. By breaking down complex ideas into manageable steps, you will gain a deeper understanding of how to approach different types of exercises.
Whether you are working through equations, graphed functions, or mathematical expressions, developing a solid grasp of the fundamentals is crucial. With clear explanations and practical techniques, you can build confidence in tackling challenges and refining your skills.
Focus on mastering the core principles to improve problem-solving strategies and achieve greater success in mathematics. Understanding the logic behind each step will empower you to apply these skills across a wide range of mathematical topics.
Algebra 1 Module 2 Answers Overview

This section provides an overview of the key topics and methods you will encounter while working through essential exercises. By understanding the fundamental principles, you can approach each problem with confidence and clarity. The focus is on breaking down complex tasks into simpler steps, allowing you to solve challenges more effectively.
As you progress through various activities, it’s important to recognize the underlying patterns and relationships between mathematical concepts. This knowledge will not only help in solving individual problems but also in connecting different types of equations and expressions. Mastering these skills will enable you to tackle more advanced topics with ease.
Being able to check your results and understand the reasoning behind each solution is crucial for developing a solid mathematical foundation. This overview aims to guide you through the process, providing a comprehensive approach to building confidence and accuracy in problem-solving.
Key Concepts Covered in Module 2
This section delves into the core principles and techniques that form the foundation for solving a variety of mathematical challenges. By understanding the relationships between different elements, you can tackle problems more strategically and with greater precision.
The primary focus includes working with expressions, equations, and functions. Emphasis is placed on recognizing patterns, simplifying complex problems, and applying step-by-step methods to find solutions. Grasping these key ideas is essential for progressing to more advanced topics and developing strong problem-solving abilities.
Step-by-Step Solutions for Practice Problems

In this section, we break down various practice problems into clear, manageable steps to help you understand the process behind finding solutions. Each problem is addressed methodically, with an emphasis on logical progression, so you can follow along and learn how to apply these strategies to similar tasks.
By following the detailed breakdown of each solution, you’ll gain insight into how to approach different types of mathematical challenges. Understanding the reasoning behind each step is crucial for building a strong foundation and improving problem-solving skills.
How to Approach Algebraic Equations
When solving mathematical equations, it’s important to follow a structured approach to simplify and isolate variables effectively. Start by identifying the key components of the equation, including constants and unknowns, before applying appropriate methods to manipulate the terms.
Understanding the rules of balancing is essential. Every operation you perform on one side of the equation must be mirrored on the other to maintain equality. By breaking down the problem step by step, you can gradually eliminate terms and simplify the equation until you isolate the desired variable.
Practice with a variety of equations to develop a deeper understanding of the different strategies, such as factoring or using the distributive property. With consistent application of these techniques, solving equations will become a more intuitive process.
Common Mistakes in Module 2 Exercises

When working through mathematical exercises, there are several common errors that learners often make. Recognizing these mistakes early can help you avoid them and improve your problem-solving skills. Many of these errors stem from misinterpreting the problem or overlooking key steps in the solution process.
One common mistake is neglecting to properly simplify expressions before moving to the next step. Failing to combine like terms or incorrectly applying operations can lead to inaccurate results. Another frequent issue is not following the correct order of operations, which can cause confusion and result in incorrect answers.
Staying mindful of each step and double-checking your work will help you catch these errors and refine your technique. With practice, you’ll become more proficient in avoiding these pitfalls and solve problems with greater accuracy.
Understanding Polynomial Operations

Polynomial operations involve manipulating expressions that contain variables raised to powers. These operations include addition, subtraction, multiplication, and division, and mastering them is essential for solving a wide range of problems. By applying specific rules to combine or separate terms, you can simplify and solve complex expressions.
Adding and Subtracting Polynomials
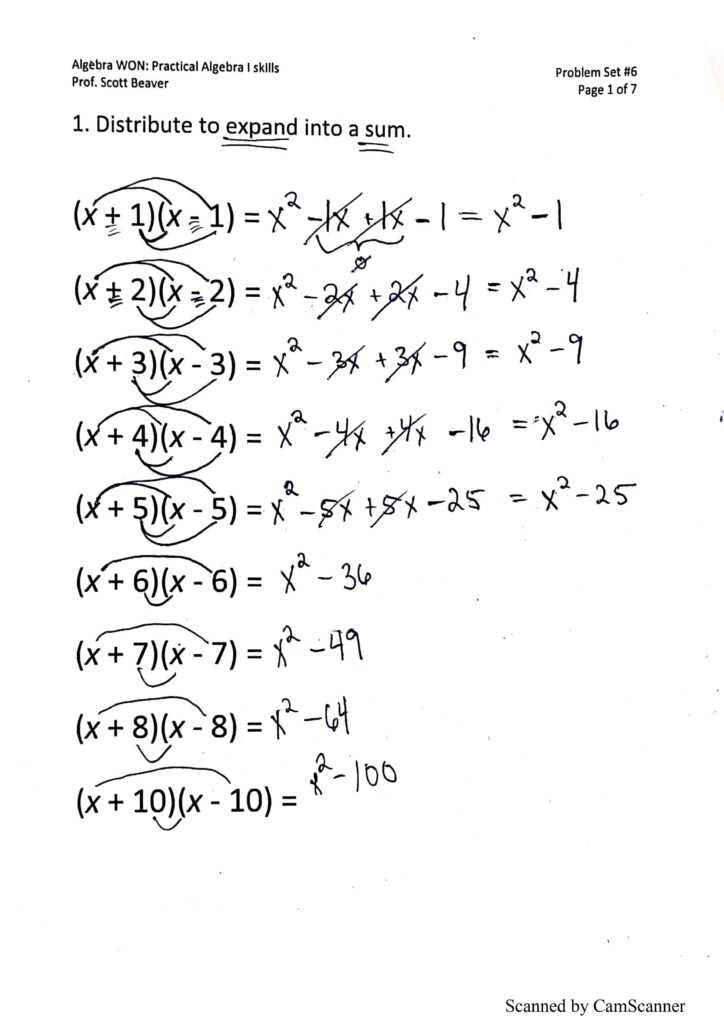
To add or subtract polynomials, you simply combine like terms. Like terms have the same variable and exponent. If the terms are not alike, they cannot be combined directly.
| Expression | Result |
|---|---|
| 3x² + 2x + 5 + 4x² – x + 7 | 7x² + x + 12 |
| 5a² + 3a – 2 – 2a² + a + 6 | 3a² + 4a + 4 |
Multiplying Polynomials
When multiplying polynomials, apply the distributive property (also known as FOIL for binomials). Multiply each term in the first polynomial by each term in the second polynomial, and then combine like terms.
| Expression | Result |
|---|---|
| (x + 3)(x + 2) | x² + 5x + 6 |
| (2a + 4)(a – 1) | 2a² + 2a – 4 |
Mastering these operations allows you to manipulate and simplify polynomials effectively, enabling you to tackle more complex problems with ease.
Solving Linear Equations Efficiently
Solving linear equations involves isolating the variable to find its value. The key to solving these types of problems efficiently is understanding the steps required to simplify and manipulate the equation without making unnecessary calculations. A structured approach ensures that you reach the correct solution with minimal effort.
Start by eliminating constants from one side and simplifying the coefficients. This often involves basic arithmetic operations such as addition, subtraction, multiplication, or division. After each step, check to ensure that the equation remains balanced, and continue simplifying until the variable is isolated.
For example, consider the equation 3x + 5 = 14. To solve it, subtract 5 from both sides to get 3x = 9, then divide both sides by 3 to find x = 3. This method allows you to solve even more complex equations quickly, making it easier to approach more advanced topics.
Using Graphs to Solve Equations
Graphs provide a visual approach to solving equations by plotting functions on a coordinate plane. By identifying where the graph of a function intersects with the axis or another graph, you can easily find the solutions to an equation. This method offers an intuitive way of understanding relationships between variables and solving for unknowns.
Steps for Graphing and Solving Equations
Follow these steps to solve an equation using graphs:
- Write the equation in a form that is easy to graph.
- Plot the equation on a coordinate plane.
- Identify the points where the graph intersects the axis or other lines.
- Use these intersection points to determine the solution(s).
Example: Solving with Graphs
Consider the equation 2x + 3 = 7. To solve this using a graph:
- Rearrange the equation to y = 2x + 3.
- Plot the line on a coordinate plane.
- Find where the line crosses the y-axis, which gives the solution for x.
Graphing is an excellent tool for understanding solutions visually and can be used for both linear and non-linear equations. By practicing this method, you can gain a deeper understanding of how equations behave and how to find solutions more effectively.
Tips for Mastering Quadratic Functions
Mastering quadratic functions requires understanding their structure and how to manipulate the equation to find solutions efficiently. The key to working with these functions is recognizing patterns in the equation and using systematic methods to solve for unknowns. With practice, you’ll become more comfortable working with quadratics and be able to solve them with ease.
Understanding the Standard Form

The standard form of a quadratic equation is written as ax² + bx + c = 0. The values of a, b, and c determine the shape and position of the graph. Recognizing the role each coefficient plays is crucial for solving and graphing the function.
Graphing and Finding the Vertex
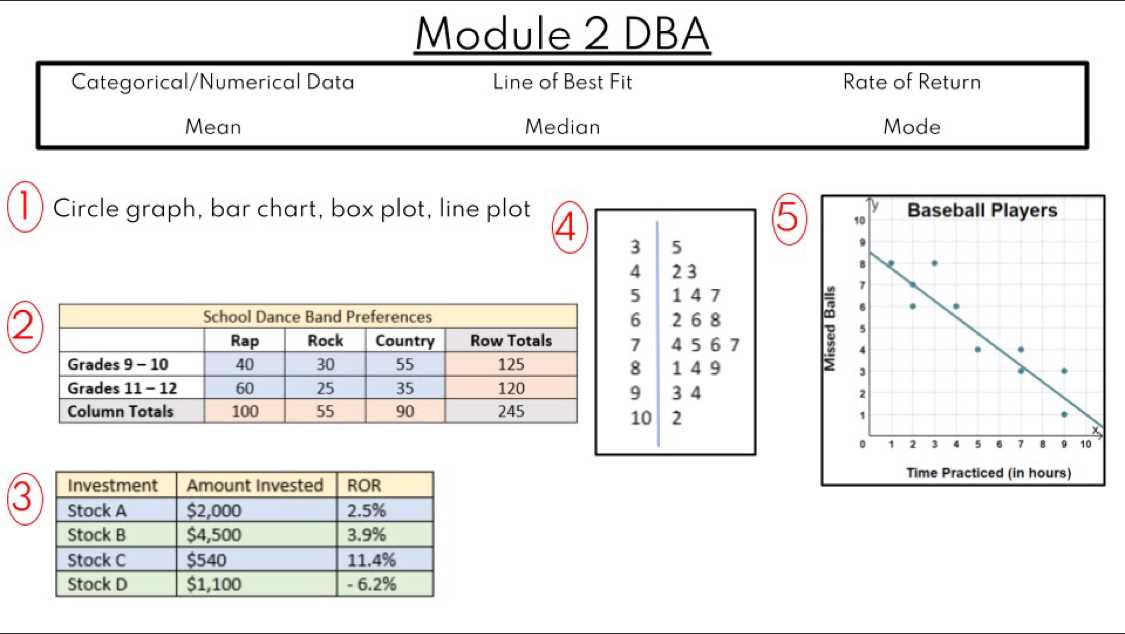
One effective way to analyze a quadratic function is by graphing it. The vertex, or the highest or lowest point on the graph, is essential for understanding the function’s behavior. Use the formula x = -b/2a to find the x-coordinate of the vertex. Once the vertex is located, you can easily graph the equation and identify key points.
Practice consistently with different quadratic functions to develop a deeper understanding of their properties and the various methods for solving them. With time, you’ll gain confidence and proficiency in handling these types of equations.
Identifying Functions and Their Graphs
Recognizing functions and understanding how their graphs behave is essential for solving a variety of mathematical problems. Functions represent relationships between variables, and their graphs provide a visual representation of these relationships. By identifying key features of the graph, such as intercepts and symmetry, you can determine the underlying function and solve for unknowns more easily.
When analyzing a graph, focus on the shape and direction of the curve. A function’s graph may be a straight line, a curve, or a more complex shape depending on the type of function. Identifying these characteristics will help you understand how the function behaves and allow you to predict its values for different inputs.
For instance, a linear function will produce a straight line, while a quadratic function will create a parabolic curve. Recognizing these patterns is a fundamental skill that will help you approach more complex problems with confidence.
Practical Examples of Algebraic Expressions
Algebraic expressions are essential tools for solving real-world problems, as they represent relationships between quantities. These expressions can be used in various practical scenarios, helping to model situations in fields like finance, engineering, and science. By understanding how to construct and manipulate these expressions, you can apply mathematical reasoning to everyday challenges.
Here are a few practical examples where algebraic expressions come into play:
- Budgeting: Suppose you have a fixed income and want to determine how much you can spend each month. An expression like y = 2000 – 500x, where x represents the number of months and y the remaining budget, helps you track spending over time.
- Distance and Speed: The formula d = rt, where d represents distance, r is rate, and t is time, is a common way to model how distance changes with speed and time.
- Temperature Change: If the temperature changes by 5 degrees per hour, you can use the expression T = 20 + 5t, where T is the temperature and t is the time in hours.
By applying algebraic expressions to these scenarios, you can solve for unknowns and make informed decisions based on the mathematical relationships at play.
Real-World Applications of Algebra 1
Mathematical concepts learned in early courses provide a solid foundation for solving a wide range of real-world problems. The ability to model situations using equations and functions allows individuals to make decisions based on data, predict outcomes, and solve practical challenges in various fields. From personal finances to engineering, the applications are endless and highly relevant in everyday life.
Applications in Everyday Life
- Budgeting and Financial Planning: People use basic equations to manage their monthly expenses, track income and savings, and plan for future purchases or investments.
- Home Improvement: When renovating or decorating, equations help calculate the amount of materials needed, such as paint, tiles, or carpet, based on room dimensions.
- Travel Planning: Calculating the cost of a trip, including fuel consumption, rental rates, and time estimates, can all be modeled with simple equations.
Applications in Professional Fields
- Engineering: Engineers use mathematical models to design structures, systems, and components, ensuring that they are safe, cost-effective, and efficient.
- Medicine: In healthcare, mathematical formulas help with drug dosage calculations, analyzing patient data, and predicting treatment outcomes.
- Technology: Programmers and software developers rely on equations to optimize algorithms, model networks, and solve complex computational problems.
In conclusion, the skills gained from solving problems and understanding relationships in mathematical terms are applicable in a variety of professions and everyday situations. The more you practice these skills, the better equipped you’ll be to handle practical challenges and make well-informed decisions.
How to Check Your Answers in Algebra
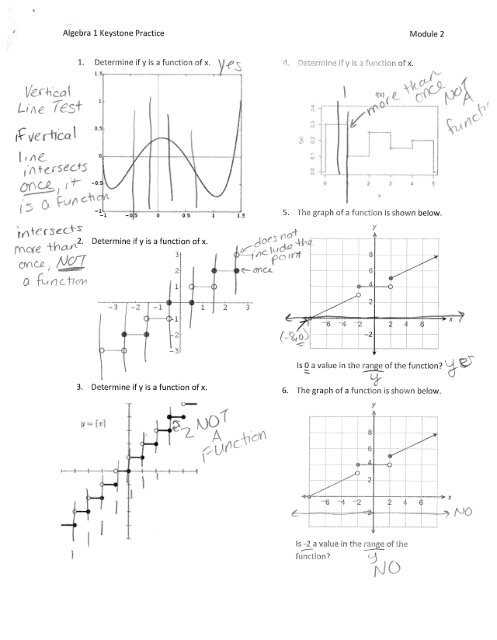
Verifying the correctness of your solutions is a crucial step in problem-solving. Double-checking your work ensures that you’ve followed the correct steps and that your final result makes sense. Using various techniques to review your solutions will help you identify any potential mistakes and improve your understanding of mathematical concepts.
Here are some strategies to check your solutions:
- Substitute the solution back into the original equation: After solving for the variable, plug your answer back into the original equation to see if both sides are equal. If they match, your solution is likely correct.
- Use an alternate method: If possible, solve the problem using a different approach or method to confirm that you arrive at the same result.
- Estimate the solution: Before solving, estimate what the solution should be. After solving, check if your answer is reasonable compared to your estimate.
- Graph the solution: If the problem involves graphing, plot the equation and check if the graph corresponds to the solution you found.
By consistently using these verification techniques, you can be more confident in the accuracy of your solutions and improve your problem-solving skills over time.
Advanced Techniques for Module 2 Problems

When tackling more complex problems, applying advanced strategies can significantly improve efficiency and accuracy. These techniques go beyond the basic problem-solving methods and provide tools to handle challenging scenarios with greater ease. By mastering these approaches, you’ll be able to solve problems more quickly and with higher confidence.
One effective strategy is breaking down complex expressions into simpler components. By recognizing patterns and applying factoring or substitution techniques, you can simplify the process and avoid errors. Another key approach is working with systems of equations, which allows you to solve for multiple variables simultaneously.
Advanced Techniques Overview
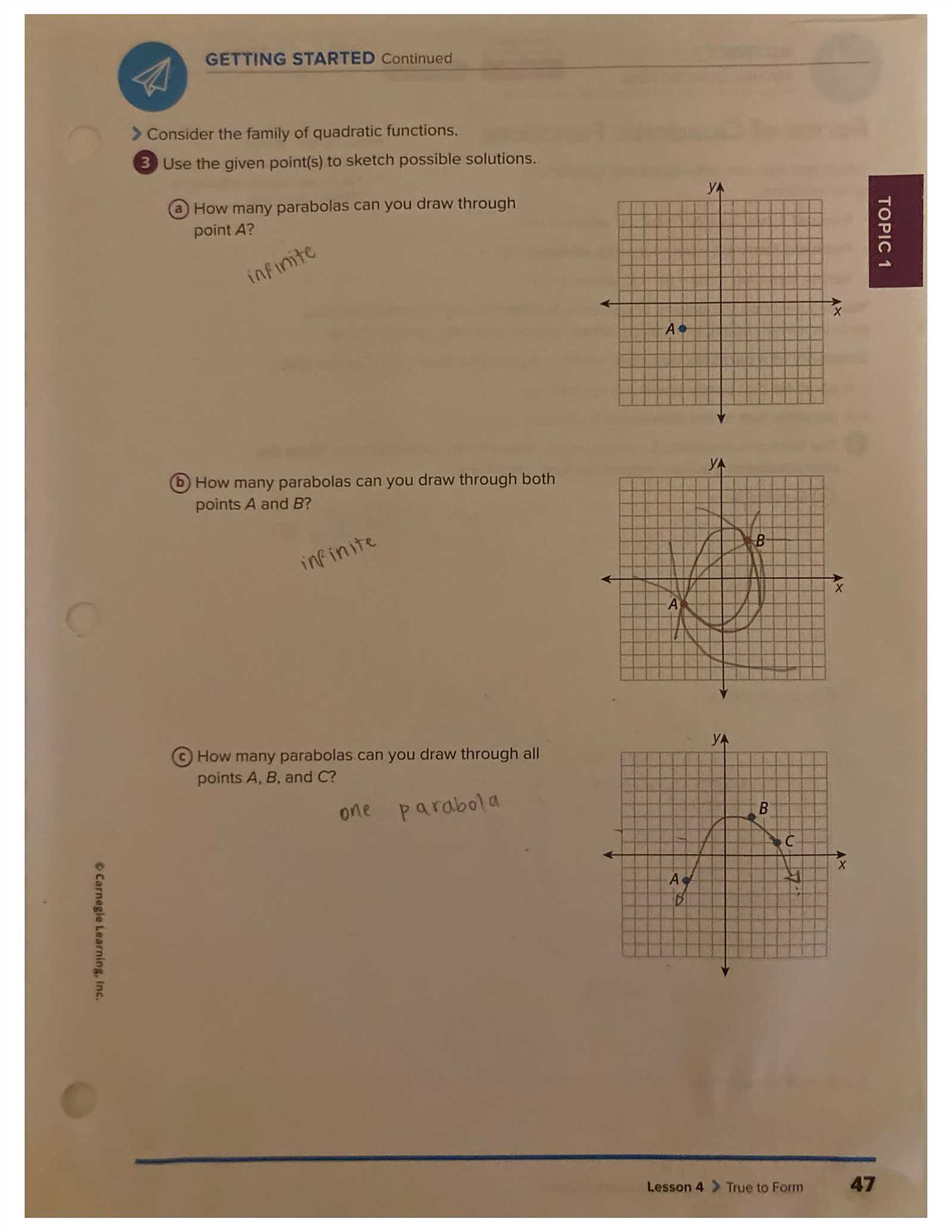
| Technique | Description |
|---|---|
| Factoring | Breaking down expressions into smaller factors to simplify and solve problems. |
| Substitution | Replacing variables with equivalent expressions to simplify equations. |
| Graphing | Visualizing equations on a graph to understand relationships and find solutions. |
| Elimination | Combining two equations to eliminate one variable and solve for the other. |
Each of these techniques has its specific applications depending on the type of problem you’re solving. Mastering them will help you approach more advanced topics and ensure that you’re equipped with the right tools for any challenge.
Strategies for Algebra 1 Success
Achieving success in mathematical problem-solving requires more than just understanding the basic concepts. It involves developing effective strategies for approaching and solving problems with confidence. By focusing on key techniques and fostering good study habits, anyone can improve their skills and succeed in more complex tasks.
Consistent Practice: Regularly working through problems is essential. Consistent practice allows you to familiarize yourself with various types of equations and develop a deeper understanding of the concepts. Set aside time each day to practice different problem types and gradually increase the level of difficulty.
Focus on Understanding, Not Memorization: Rather than memorizing formulas, focus on grasping the underlying principles behind them. Understanding how and why certain methods work will give you the ability to apply them in different scenarios. This approach is much more effective in the long term.
Use Multiple Learning Resources: Don’t rely solely on one textbook or method of instruction. Supplement your learning with online tutorials, videos, and practice worksheets. Different perspectives can help clarify complex ideas and give you a more well-rounded understanding of the material.
Seek Help When Needed: If you’re struggling with a particular concept or problem, don’t hesitate to ask for help. Whether it’s a teacher, tutor, or study group, getting assistance early can prevent misunderstandings from snowballing into bigger challenges.
Stay Organized: Keep your notes, assignments, and solutions well-organized. A clean and structured approach will make it easier to review key points and track your progress. Consider using a dedicated notebook or digital tool to organize your work and review past problems.
Resources for Additional Algebra Practice
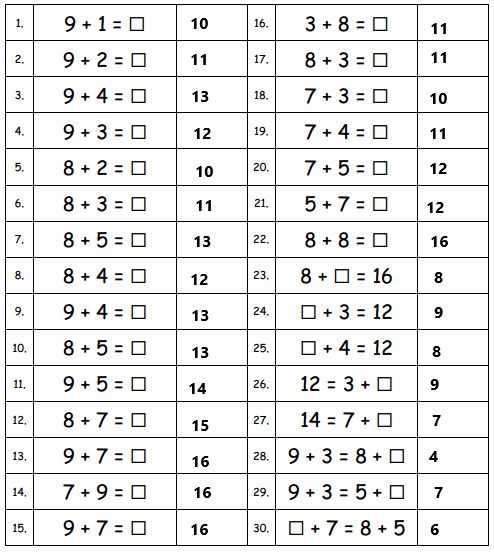
Practicing mathematical skills outside of regular classwork can significantly enhance understanding and performance. Whether you’re looking for extra worksheets, interactive tools, or helpful tutorials, there are numerous resources available to support continued learning and skill-building.
Online Platforms
Many websites offer interactive lessons and practice problems tailored to different skill levels. These platforms often provide immediate feedback, which can help you pinpoint areas that need improvement.
- Khan Academy: Offers free lessons and practice problems, making it easy to review and learn at your own pace.
- IXL: Provides personalized practice with a focus on mastery of specific topics.
- Brilliant.org: Offers a wide range of engaging problems that help reinforce key concepts through problem-solving.
Books and Workbooks
For those who prefer working on paper, various textbooks and workbooks are designed to reinforce learning through additional problems and explanations. These can be useful for self-study or for getting ahead in topics.
- Practice Makes Perfect: Pre-Algebra by Laila K. B. Madania: A workbook filled with practical problems and solutions.
- Algebra 1 Workbook for Dummies: A comprehensive guide with additional problems to help reinforce your understanding.
Study Groups and Tutoring: Engaging with a study group or hiring a tutor can be beneficial for personalized instruction. Collaborative learning helps clarify difficult concepts and reinforces what you’ve learned.