Scientific Notation Word Problems Worksheet with Answers

Understanding how to manage extremely large or small quantities is essential for solving many mathematical and scientific challenges. These techniques are widely used in fields such as physics, engineering, and computer science, where dealing with vast ranges of values is common. By learning how to express and manipulate these numbers efficiently, you gain the ability to tackle complex scenarios with ease.

In this guide, you’ll be introduced to a series of practical exercises designed to sharpen your skills in working with large-scale numerical expressions. These activities focus on simplifying difficult calculations and help you approach real-life scenarios that require precision and clarity.

Mastering this skill not only boosts your problem-solving capabilities but also enhances your understanding of advanced topics. Each example is crafted to guide you through the process step-by-step, ensuring that you can apply the concepts confidently and accurately in various contexts.

Scientific Notation in Real Life

In many fields, professionals encounter values that are either exceedingly large or extremely small. For example, measurements in astronomy or biology often involve numbers beyond the capacity of regular calculators. Using an efficient system to handle such quantities is crucial to making sense of data and ensuring accuracy. This approach simplifies complex calculations, making it easier to understand and communicate results in everyday situations.

Applications in Science and Engineering

In scientific research and engineering, large figures are commonly used to express the size of distant galaxies, the volume of tiny particles, or the energy involved in nuclear reactions. These values are often written in a compact form to make calculations more manageable and prevent errors from lengthy expressions.

Practical Examples in Technology

In technology, particularly in computing, extremely small measurements like nanoseconds and the size of microchips are regularly encountered. Representing these values efficiently allows for quick processing and clear communication of technical specifications. Below are some common real-world uses:

Field	Example	Value
Astronomy	Distance to a star	4.22 × 1016 km
Physics	Mass of a proton	1.67 × 10-27 kg
Technology	Data transfer rate	1 × 109 bits/sec
Biology	Size of a bacterium	2 × 10-6 m

By using this method, professionals in diverse fields can simplify their calculations, avoid mistakes, and communicate results more effectively. Whether in scientific experiments, engineering projects, or technological advancements, expressing values in this form is an invaluable tool for clarity and precision.

Understanding the Basics of Scientific Notation

To simplify calculations involving very large or very small numbers, we use a system that allows us to represent these values in a more compact form. This system helps to avoid the challenges of writing and working with long strings of digits, making it easier to perform arithmetic and express quantities clearly. The core idea is to express numbers as a product of a base and an exponent.

Here are some basic principles that define this system:

• Base: A number is expressed as a multiple of a power of 10.
• Exponent: The exponent represents how many times the base (10) is multiplied or divided.
• Positive Exponent: Used for numbers greater than 1.
• Negative Exponent: Used for numbers less than 1.

For example, the number 5,000 can be written as 5 × 10³, where 5 is the base, and 3 is the exponent. Similarly, a small number like 0.0003 is written as 3 × 10^-4.

How to Convert Numbers

Converting large and small values into this format involves identifying the number of places the decimal point must be moved to reach the desired base. The exponent reflects this shift:

1. For numbers greater than 1, move the decimal to the left and use a positive exponent.
2. For numbers less than 1, move the decimal to the right and use a negative exponent.

Consider the example of converting 0.00012:

• Move the decimal 5 places to the right, so the number becomes 1.2 × 10^-4.

By understanding these basics, you can more easily work with extreme values in mathematics, science, and engineering, simplifying complex calculations.

How to Solve Scientific Notation Problems

To tackle calculations involving large and small numbers, it’s important to break down the process into manageable steps. The goal is to simplify expressions that involve powers of 10, making complex calculations more straightforward. By following a few essential rules and strategies, you can solve these types of challenges quickly and accurately.

Step-by-Step Approach

Here’s a basic method for handling these kinds of calculations:

1. Identify the Base and Exponent: Look at the given values and determine the base (usually 10) and the exponent. For example, in 4 × 10⁵, the base is 10, and the exponent is 5.
2. Adjust the Exponents: When multiplying or dividing numbers, you’ll need to adjust the exponents based on the operation. Add the exponents when multiplying, and subtract them when dividing.
3. Perform the Arithmetic: After adjusting the exponents, perform the necessary multiplication or division with the base values. Keep in mind that the result should maintain the same exponent format.
4. Final Check: Ensure that the result is in proper form, meaning the base is between 1 and 10. If not, adjust the exponent accordingly.

Example: Multiplying Numbers

To multiply 3 × 10⁴ by 2 × 10⁶, follow these steps:

• Multiply the base values: 3 × 2 = 6.
• Add the exponents: 4 + 6 = 10.
• The result is: 6 × 10¹⁰.

This process can be applied to both addition and subtraction of such expressions, with slight modifications in how you handle the exponents. By following these guidelines, you’ll be able to confidently solve a wide range of calculations involving large or small numbers.

Importance of Scientific Notation in Math

In mathematics, dealing with extremely large or small numbers is a common challenge. Without an efficient way to express these quantities, calculations become cumbersome, error-prone, and difficult to manage. Using a simplified method to represent these values is crucial for accuracy and ease of computation, especially in fields like algebra, calculus, and geometry.

This approach plays a vital role in allowing mathematicians, engineers, and scientists to work more efficiently. It ensures that complex expressions remain manageable, helping to prevent mistakes when performing arithmetic operations or solving equations. Moreover, it allows for clear communication of results across various disciplines, from theoretical work to practical applications.

By using this system, students and professionals alike can handle extreme values with confidence, transforming complex problems into simpler tasks. This not only saves time but also reduces the risk of miscalculations, making it an indispensable tool in modern mathematics.

Step-by-Step Guide for Word Problems

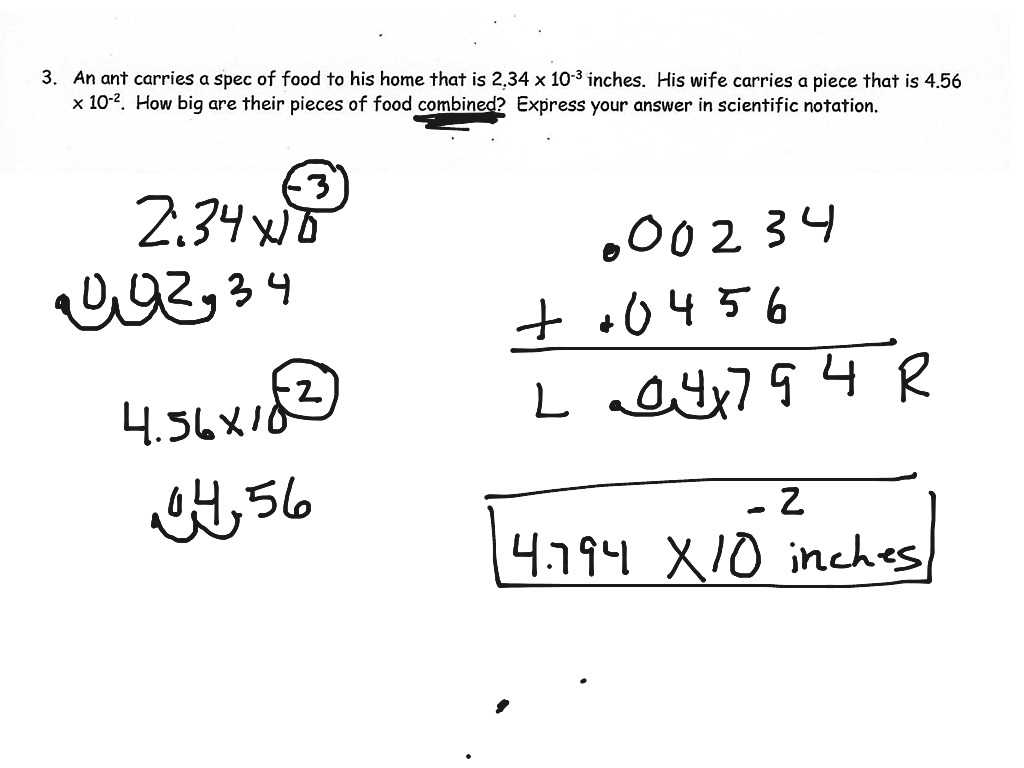
When faced with challenges involving large or small quantities, it’s essential to break down the steps in a systematic manner. By approaching each task methodically, you can simplify the process and ensure accurate results. Whether you’re dealing with multiplication, division, or addition of values expressed in compact forms, following a clear structure can help you solve the problem more effectively.

Steps for Solving Challenges

Here’s a simple guide to tackling these types of exercises:

1. Read the Problem Carefully: Understand the values and operations involved before making any calculations.
2. Identify Key Quantities: Extract the numbers and their respective powers of 10.
3. Perform the Required Arithmetic: Follow the rules for adding, subtracting, multiplying, or dividing exponents, as needed.
4. Write the Final Answer: Ensure the result is expressed in proper form and clearly communicates the solution.

Example Breakdown

Consider the following example: You need to multiply 3.2 × 10⁵ by 4.1 × 10³. Here’s how to proceed:

Step	Action	Result
1	Multiply the base numbers: 3.2 × 4.1	13.12
2	Add the exponents: 5 + 3	108
3	Write the final result	13.12 × 108

By following this process, the problem becomes more straightforward, and you can confidently arrive at the correct result. This step-by-step method applies to various types of challenges, helping you solve even the most complex expressions efficiently.

Common Mistakes in Scientific Notation

While working with values expressed in compact forms, it’s easy to make mistakes, especially when handling large numbers or small decimals. Many errors occur due to misunderstanding the rules for manipulating exponents or incorrectly applying arithmetic operations. Recognizing these common pitfalls can help you avoid unnecessary confusion and ensure accurate results.

Here are a few frequent mistakes to be aware of:

• Incorrect Handling of Exponents: One of the most common errors is failing to correctly add or subtract exponents when multiplying or dividing numbers. It’s essential to adjust the exponent based on the operation being performed.
• Misplacing the Decimal Point: When converting between forms or performing operations, it’s crucial to shift the decimal point accurately. A small error here can lead to a significant mistake in the result.
• Forgetting to Adjust the Exponent: Sometimes, after moving the decimal point, the exponent must be adjusted to maintain the correct value. Failing to make this adjustment can result in an incorrect final answer.
• Using Incorrect Powers of Ten: Another mistake involves using the wrong power of 10 when converting between standard and compact form. It’s important to carefully count the number of decimal shifts to avoid errors in the exponent.

By staying mindful of these common errors and double-checking your work, you can improve your accuracy and efficiency when dealing with these types of expressions. This awareness will help you handle even the most complex calculations with confidence.

Using Exponents in Word Problems

When tackling exercises that involve extremely large or small numbers, exponents offer an efficient way to express and manipulate these values. By applying the rules of exponents, you can simplify calculations, making complex scenarios more manageable. This is especially useful in real-world situations like calculating distances, areas, or even scientific measurements where large numbers are involved.

In these types of exercises, the key is to correctly interpret the relationship between the numbers and their powers. Whether you’re multiplying or dividing values, adjusting exponents allows for easier handling of quantities that would otherwise be too cumbersome to work with. Understanding how to manipulate exponents properly can greatly improve both speed and accuracy in problem-solving.

For example, when dealing with population sizes, distances in space, or measurements in physics, exponents allow you to express these quantities in a compact, more manageable form. A well-defined approach to using exponents will enable you to solve these kinds of challenges effectively.

Examples of Real-World Applications

Large and small quantities are common in many fields, from space exploration to medicine, and are often represented using compact forms for simplicity and ease of calculation. These methods are used to express values that are either extremely large, like distances between planets, or incredibly small, such as the size of atoms or particles. In practical scenarios, understanding how to work with such expressions can lead to more efficient solutions and clearer communication in various disciplines.

Space Exploration

In astronomy and space exploration, distances between stars, galaxies, and planets are often expressed using exponents. For example, the distance from Earth to the nearest star, Proxima Centauri, is approximately 4.24 × 10¹³ kilometers. This allows astronomers to handle vast distances more easily and compare them without dealing with unwieldy numbers.

Biology and Medicine

In the field of biology, scientists often work with very small quantities, such as the size of cells or the number of bacteria in a sample. For instance, the average size of a human red blood cell is about 8 × 10^-6 meters. This compact form makes it easier to communicate measurements that would otherwise be difficult to interpret or work with in standard decimal form.

By using these expressions in real-world applications, professionals can simplify calculations, avoid errors, and work more efficiently. Whether handling large measurements in space or small values in the lab, this method provides a consistent and practical way to represent and manipulate quantities in many scientific fields.

Tips for Solving Complex Problems

When faced with intricate tasks involving large or small quantities, it’s important to approach them systematically. By breaking down the exercise into smaller, simpler steps, you can better manage and solve each part. This organized method helps reduce errors and ensures that the solution is both accurate and efficient.

Approach and Strategies for Efficiency

Here are several tips to simplify complex calculations and improve your problem-solving process:

• Carefully Analyze the Situation: Before jumping into calculations, take time to fully understand the task. Identify the key elements involved and what is being asked.
• Convert Large and Small Quantities: When numbers become unwieldy, consider rewriting them in more manageable forms using powers of ten. This can significantly simplify your work.
• Work Through Step by Step: Break the task into smaller components. Solve one part at a time and then combine the results. This makes the problem more digestible.
• Track Units and Exponents: Be mindful of the units you’re working with and the rules for handling exponents. Consistency in both areas is crucial to avoid mistakes.
• Double-Check Your Operations: When performing operations such as addition or subtraction of exponents, ensure you’re following the correct procedures. Mistakes here can throw off the entire calculation.

Example Problem Breakdown

Consider the following example: You need to divide 5.6 × 10⁹ by 2.0 × 10⁴. Let’s apply the steps:

Step	Action	Result
1	Divide the base numbers: 5.6 ÷ 2.0	2.8
2	Subtract the exponents: 9 – 4	105
3	Write the final result	2.8 × 105

By following these strategies, you’ll be able to approach complex tasks with more confidence and ease. Breaking the problem into smaller, manageable steps makes it easier to navigate, reducing the chances of errors and improving your efficiency in finding the correct solution.

Why Scientific Notation Is Essential

In many areas of mathematics and science, handling extremely large or small numbers is a routine task. These values often appear in fields like astronomy, physics, and engineering, where precision is key. Using a compact and efficient way to represent these numbers makes calculations more manageable and ensures accuracy in further computations.

One of the primary reasons this method is so crucial is that it simplifies complex arithmetic. By reducing the number of digits and focusing on the most significant figures, it becomes easier to perform operations such as multiplication, division, and addition. Without this system, working with massive values would be time-consuming and error-prone.

Additionally, this system allows for a consistent way of expressing both very large and very small quantities. Whether dealing with the mass of planets or the size of microscopic particles, this method ensures that the scale of numbers remains clear and understandable, avoiding confusion between different magnitudes.

Real-World Impact

From calculating the distance between stars to determining the growth of bacteria, being able to represent and manipulate extremely large or small values is vital for accuracy and efficiency. This method enables professionals across fields to carry out complex analyses without getting bogged down by the cumbersome nature of traditional number formats.

Precision and Efficiency

In practice, this approach increases both precision and speed when working with high-level mathematics. For example, when calculating the speed of light or the age of the universe, the traditional way of writing these numbers would be unwieldy. Instead, a simplified representation helps keep the problem-solving process clean and focused on the solution.

Converting Large Numbers with Ease

Handling large numbers can often seem daunting, but with the right approach, the task becomes much simpler. By expressing these values in a more compact form, you can easily compare, manipulate, and calculate them without feeling overwhelmed. This method allows you to work efficiently, saving both time and effort when performing complex mathematical operations.

When dealing with exceptionally large values, it’s essential to break them down into more manageable components. Using this system, you can represent vast quantities, such as the distance between stars or the size of particles, in a format that simplifies their manipulation. Instead of dealing with dozens of digits, you can focus on just the significant figures and the scale of the number, making the entire process more efficient.

Steps to Convert Large Numbers

To convert large values into a more concise format, follow these simple steps:

• Identify the decimal point: Find the decimal point in the number and note how many places it must be moved to get the number into a more standard form.
• Move the decimal point: Shift the decimal point to the right for large numbers until the value is between 1 and 10.
• Count the shifts: The number of places you moved the decimal point will determine the exponent for 10.
• Write in compact form: Write the resulting number as a product of the shifted value and 10 raised to the power of the number of decimal shifts.

Example of Conversion

Let’s consider the number 150,000,000,000. To convert it:

• Start with the decimal point after the first digit: 1.5.
• Count how many places the decimal must move to get from 1.5 to 150,000,000,000, which is 11 places.
• Write the result as 1.5 × 10¹¹.

This simple approach makes it much easier to work with large numbers, allowing for more efficient problem-solving and calculations in various mathematical contexts.

Practical Exercises for Students

Hands-on practice is essential when learning to work with large and small numbers, as it helps solidify understanding and build confidence. By engaging in various exercises, students can sharpen their skills and apply their knowledge in real-world contexts. These activities encourage critical thinking and allow students to practice the techniques they have learned in a structured way.

To master this skill, it’s important to complete a series of exercises that involve converting numbers, performing operations, and solving real-life scenarios. These tasks not only improve mathematical abilities but also demonstrate the practical value of these concepts in various fields such as science, engineering, and technology.

Exercise Examples

Here are some example activities for students to work on:

• Converting large numbers: Given numbers like 98,000,000,000, students should convert them into a more manageable form. For example, converting this number into 9.8 × 10¹⁰.
• Performing arithmetic operations: Have students multiply or divide numbers in compact form. For instance, multiplying 3.5 × 10⁶ by 2 × 10³.
• Real-world application: Challenge students to calculate the distance between two cities using numbers expressed in this format, or measure the size of particles in a lab experiment.

Step-by-Step Approach

Encourage students to follow these steps to solve the exercises:

1. Read the problem carefully and identify the key information.
2. Convert large or small numbers into the appropriate format.
3. Perform the necessary arithmetic operation (addition, subtraction, multiplication, division).
4. Check the result by converting it back to the original number or comparing it with an expected value.

By completing these exercises, students will become more comfortable and proficient in handling large and small values, making mathematical tasks more efficient and less intimidating.

How to Check Your Answers

Reviewing your work is an essential step in solving any mathematical task, as it ensures accuracy and reinforces the understanding of the concepts. When working with large or small numbers, double-checking calculations can help prevent errors and identify where adjustments are needed. It’s important to have a systematic approach to verify the results after completing each exercise.

The process of checking your results involves revisiting each step you took, looking for mistakes in conversion, arithmetic, or application of the rules. By using alternative methods, such as recalculating or approximating, you can ensure that your final solution is correct. Additionally, taking time to reflect on the reasoning behind each step is crucial for building confidence in the solution.

Methods for Verification

Here are several approaches you can use to check your work:

• Reversing the calculation: If you multiplied two numbers, divide the result by one of the original numbers to confirm the answer. Similarly, if you added or subtracted, check if the inverse operation brings you back to the original values.
• Estimation: Round the numbers to simpler values before performing the calculation and compare the result with the approximate answer. If the calculated result is too far from the estimate, there may be an error.
• Alternative method: Use a different approach or technique to solve the problem, and compare the results to see if they match. This can be particularly helpful in complex tasks.

Common Mistakes to Watch Out For

While verifying, be mindful of common errors that can creep in:

• Forgetting to adjust the exponent correctly when converting numbers.
• Misplacing the decimal point or incorrectly performing multiplication or division.
• Failing to consider significant figures when simplifying answers.

By following these verification techniques and remaining aware of potential mistakes, you can ensure that your calculations are accurate and that you have a deep understanding of the concepts at hand.

Scientific Notation in Science and Engineering

In many scientific and engineering fields, working with extremely large or small numbers is a common challenge. These numbers often arise in areas such as physics, chemistry, astronomy, and electrical engineering, where measurements can span a wide range of magnitudes. To simplify calculations and communicate results efficiently, a specialized method for representing these values is essential. This approach allows for easier manipulation, comparison, and understanding of complex figures.

One of the main advantages of this method is its ability to condense very large or very small numbers into a more manageable form. This enables scientists and engineers to express values that would otherwise require cumbersome notation or extensive use of zeros. The ability to work with these simplified forms improves accuracy in calculations, reduces the potential for mistakes, and saves time in both research and practical applications.

Applications in Various Fields

Different scientific and engineering disciplines frequently utilize this method to address problems involving large or small quantities. Some common areas where this technique is widely applied include:

• Astronomy: Distances between celestial bodies, such as stars and planets, often require the use of large numbers. By representing these distances using a more concise format, astronomers can perform calculations more effectively.
• Physics: Physical constants, such as the speed of light or gravitational forces, are often represented using this method to simplify equations and make the constants easier to work with in complex calculations.
• Chemistry: The size of atoms or molecules, as well as the amounts of substances involved in chemical reactions, frequently require very small numbers, which are easier to handle using this system.
• Electrical Engineering: When dealing with measurements such as resistance, voltage, or power, which can vary over a wide range, this approach provides a convenient way to express values accurately.

Benefits in Engineering Calculations

In engineering, this method allows for a high degree of precision, even when working with numbers that vary across several orders of magnitude. Some of the key benefits include:

• Improved Calculation Speed: Using a standardized format helps engineers perform computations more quickly by reducing the need to manually adjust values with many zeros.
• Enhanced Accuracy: This method minimizes the likelihood of errors that may occur when dealing with extremely large or small numbers.
• Ease of Communication: Representing values in this way makes it easier for professionals to share information across different fields and levels of expertise, as the format is universally recognized.

Overall, this technique plays a crucial role in simplifying complex mathematical tasks across various scientific and engineering disciplines, allowing for greater precision and more efficient workflows.

Key Formulas for Word Problems

In many mathematical tasks, especially those that deal with complex numbers or measurements, understanding and applying the correct formulas is essential for accurate results. The ability to transform abstract information into solvable equations can help simplify what initially seems like a challenging question. This section explores some of the most important formulas used in solving real-life mathematical scenarios, making it easier to approach and solve calculations involving large or small numbers.

Common Formulas Used in Everyday Calculations

Several fundamental formulas form the backbone of various calculation methods in both academic and practical settings. Here are some of the essential ones:

• Distance Formula: d = rt (where d is distance, r is rate, and t is time) – This formula is useful for calculating travel or movement over time at a constant speed.
• Area of a Circle: A = πr² (where A is the area and r is the radius) – This formula helps calculate the area of a circular surface, often used in fields like engineering and construction.
• Volume of a Rectangular Prism: V = l × w × h (where V is volume, l is length, w is width, and h is height) – Essential for determining the space inside three-dimensional objects, commonly used in physics and architecture.
• Force Formula: F = ma (where F is force, m is mass, and a is acceleration) – This equation is key in understanding basic principles of motion in physics.

Application of Formulas in Real-Life Situations

Understanding how to apply these formulas to real-world situations is crucial for solving problems effectively. Below are examples of how these formulas are used:

• Example 1: If a car travels at 60 miles per hour for 2 hours, the distance covered can be calculated by the formula d = rt. Here, r is 60 mph, and t is 2 hours, so d = 60 × 2 = 120 miles.
• Example 2: To find the area of a circular field with a radius of 10 meters, use the formula A = πr². With r = 10, the area becomes A = π × 10² = 314.16 square meters.
• Example 3: To calculate the volume of a box with a length of 5 meters, a width of 3 meters, and a height of 4 meters, apply the formula V = l × w × h. The volume is V = 5 × 3 × 4 = 60 cubic meters.
• Example 4: If a 10 kg object accelerates at 3 meters per second squared, the force exerted can be found using F = ma, resulting in F = 10 × 3 = 30 newtons.

Mastering these basic formulas allows students and professionals alike to break down complex tasks into manageable steps, ensuring accurate results in various mathematical and practical applications.

Using a Worksheet to Improve Skills

One of the most effective ways to enhance your abilities in solving mathematical tasks is through consistent practice. By working through a series of exercises, you can strengthen your understanding and application of various concepts. A set of problems designed to target specific areas helps identify weaknesses and allows for focused improvement. This approach makes it easier to track progress and refine techniques, ensuring mastery of each step involved.

Practicing regularly allows for better retention of formulas and methods, enabling quicker and more accurate solutions in future challenges. It also builds confidence, as repetitive exercises provide a deeper familiarity with common patterns and techniques. Whether you’re working through simple calculations or tackling more complex scenarios, structured practice is a key element in developing strong problem-solving skills.

By incorporating a variety of tasks into your practice routine, you ensure that you’re not only reinforcing learned techniques but also expanding your capability to tackle new and unfamiliar situations. Through deliberate and targeted efforts, improvement is both achievable and measurable.