Big Ideas Learning Geometry Chapter Resources and Answers

Mathematics is a subject that builds upon a series of key principles and techniques. To master these concepts, it is essential to understand each topic thoroughly and practice solving related problems. This guide provides a structured approach to exploring different mathematical topics, offering solutions and strategies that enhance comprehension and improve problem-solving skills.

Each section of this material focuses on specific topics, breaking them down into smaller, manageable parts. Whether it’s understanding fundamental principles or tackling more complex challenges, this resource offers the support needed to progress step by step. With carefully selected examples and detailed explanations, learners can strengthen their grasp of critical mathematical concepts and apply them with confidence.

Big Ideas Learning Geometry Chapter Resources

Mastering mathematical topics requires a methodical approach that builds a strong foundation of understanding. This section presents a comprehensive guide to help learners navigate various mathematical concepts, offering targeted solutions and explanations for each theme. By exploring key sections, students can develop a deeper comprehension of the subject and enhance their problem-solving skills.

Detailed Breakdown of Each Topic

Each subject area is presented with clarity and structure, ensuring that complex ideas are broken down into simpler, more digestible parts. From basic principles to advanced techniques, the information is designed to foster a step-by-step understanding, allowing learners to progress at their own pace. With practical examples and well-organized explanations, this section provides a solid framework for tackling mathematical challenges.

Practical Tips for Mastery

In addition to theoretical explanations, this guide includes practical tips and strategies for effective study. These techniques are intended to help learners apply their knowledge to real-world problems, ensuring they gain confidence in their mathematical abilities. Through continuous practice and application, students can refine their skills and achieve mastery in the subject.

Overview of Big Ideas Geometry Curriculum

The curriculum offers a structured pathway for understanding the core principles of mathematical reasoning. It emphasizes key topics that build on one another, guiding students from foundational concepts to more advanced applications. Each section is designed to provide learners with the tools and knowledge they need to apply theoretical ideas to practical problems, ensuring a solid grasp of essential mathematical skills.

The material is divided into specific units, each focusing on a particular area of mathematics. These units are carefully crafted to provide a progressive learning experience, incorporating both theoretical understanding and hands-on practice. Below is a table outlining the primary themes covered throughout the curriculum:

Unit	Focus Area	Key Concepts
Unit 1	Basic Shapes and Properties	Types of shapes, properties of triangles, quadrilaterals, and circles
Unit 2	Lines and Angles	Parallel lines, angles, angle pairs, and theorems
Unit 3	Measurement and Perimeter	Area and perimeter calculations, surface area, and volume
Unit 4	Coordinate Plane	Graphing points, distance formula, and slope
Unit 5	Transformations	Translations, rotations, reflections, and dilations

Through this structured approach, students develop the necessary skills to solve both theoretical and practical problems, building a strong foundation in mathematics that can be applied in various real-world situations.

How to Use Geometry Chapter Answers

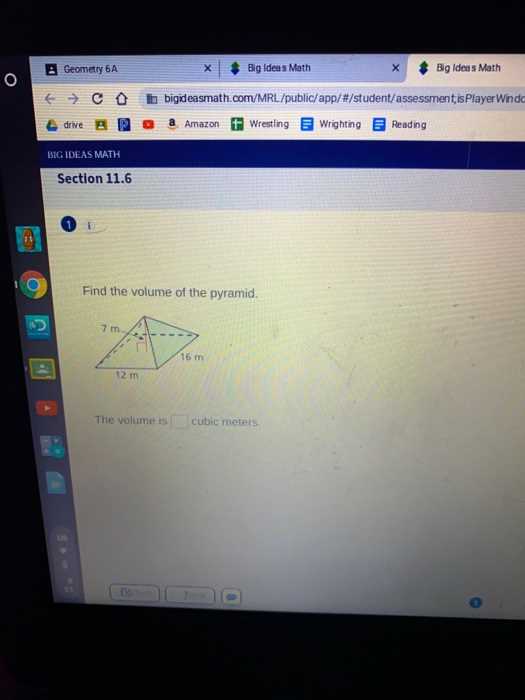
To effectively grasp mathematical concepts, it is essential to utilize solutions in a way that reinforces understanding and enhances learning. The provided solutions are not just for checking correctness but also serve as a valuable tool for identifying key techniques and approaches used to solve problems. By studying each solution closely, students can uncover the underlying principles and methods that contribute to the correct answer.

Start by attempting problems on your own first. Afterward, compare your approach with the provided solution. Focus on understanding each step taken in the solution process, paying attention to the reasoning and strategies applied. This will help you see different methods of problem-solving and improve your ability to tackle similar problems in the future. Don’t just memorize the steps–ensure that you fully comprehend why each step is necessary and how it contributes to the final result.

Additionally, use the explanations to identify areas where you may need further practice. If a particular concept or step isn’t clear, revisit it and try different types of problems to strengthen your grasp. With this methodical approach, you’ll be able to build confidence and improve your skills over time.

Understanding Key Concepts in Geometry

A solid understanding of fundamental principles is the foundation of success in any mathematical field. By mastering the core concepts, students can confidently approach increasingly complex problems. This section focuses on key themes that are essential for building a strong base in mathematics, from shapes and measurements to spatial reasoning and transformations.

Essential Topics to Focus On

• Shapes and Figures: Learn the properties of different polygons, including triangles, quadrilaterals, and circles.
• Angles and Relationships: Understand various types of angles, their relationships, and how they interact within shapes.
• Measurement Techniques: Grasp how to calculate area, perimeter, and volume for different geometric shapes.
• Coordinate System: Master graphing points, lines, and understanding the plane for visualizing geometric figures.

Key Strategies for Mastery

1. Start with a clear understanding of the definitions and properties of each geometric figure.
2. Practice visualizing shapes and their properties to enhance spatial awareness.
3. Work through examples and problems that reinforce the concepts and improve problem-solving skills.
4. Use diagrams and drawings to better understand relationships between different geometric elements.

By focusing on these key areas and applying strategies to reinforce your knowledge, you can develop a deeper understanding of the subject and build the skills necessary to solve more advanced problems.

Effective Study Tips for Geometry

Mastering mathematical concepts requires a focused and strategic approach. To excel in this field, it’s crucial to adopt study habits that foster both understanding and retention. With the right techniques, complex ideas become more accessible, and problem-solving skills improve steadily. The following tips provide a structured method to help students navigate through challenging topics and strengthen their grasp of important principles.

• Understand the Fundamentals: Start by mastering basic definitions and properties. A strong foundation in the basics ensures success as you move to more advanced concepts.
• Use Visual Aids: Diagrams, graphs, and drawings help to visualize problems and make abstract concepts more tangible. Sketching figures can often simplify complex relationships.
• Break Problems Into Steps: Approach each problem methodically. Break it down into smaller, manageable steps to avoid feeling overwhelmed and to identify the solution process clearly.
• Practice Regularly: Repetition is key in mathematics. Consistent practice helps reinforce concepts, making them easier to apply during tests or real-life situations.
• Seek Clarification When Needed: If you’re stuck on a particular topic or method, don’t hesitate to ask for help. Understanding where you went wrong is crucial for progress.

By implementing these study strategies, students can approach each lesson with confidence, ensuring a more effective learning experience and improving overall performance in mathematics.

Geometry Chapter 2: Lines and Angles

In this section, we focus on understanding the fundamental elements that define shapes and their relationships. Lines and angles are the building blocks of more complex geometric figures, and mastering these concepts is essential for solving problems involving shapes and their properties. By exploring the properties and relationships between lines and angles, students can develop a strong foundation for tackling more advanced topics in geometry.

Key Concepts in Lines and Angles

• Types of Lines: Parallel lines, perpendicular lines, and intersecting lines, each with distinct properties.
• Angle Types: Acute, obtuse, right, and straight angles–understanding their definitions and measurements.
• Angle Pairs: Complementary, supplementary, and vertical angles and how they relate to one another.
• Transversals: How a transversal intersects parallel lines and the resulting angle pairs.

Strategies for Mastery

1. Identify and label all lines and angles in diagrams to clearly visualize the relationships between them.
2. Practice calculating angle measurements using the properties of angle pairs and parallel lines.
3. Use real-world examples, such as architectural designs or road networks, to see how lines and angles apply in everyday life.

Understanding the relationships between lines and angles is essential for solving more complex problems. By practicing and applying these basic concepts, students can build confidence and prepare for more advanced topics.

Chapter 3: Properties of Triangles

This section focuses on the fundamental characteristics of triangles, which are one of the most basic yet versatile shapes in mathematics. Understanding the properties of triangles allows students to solve various geometric problems, from calculating angles to determining side lengths. By exploring different types of triangles and their unique properties, learners can build a solid foundation for more advanced studies in geometry.

Triangles have distinct properties depending on their side lengths and angle measurements. Recognizing these differences is essential for solving a variety of problems, including those involving congruence, similarity, and the Pythagorean theorem. The following table outlines the main properties of different types of triangles:

Type of Triangle	Properties	Examples
Equilateral	All sides and angles are equal; each angle is 60°.	All sides have the same length, and angles are congruent.
Isosceles	Two sides are equal, and two angles are congruent.	Two equal sides with two equal angles opposite them.
Scalene	No sides or angles are equal.	All sides have different lengths and all angles have different measures.
Right	One angle is 90°.	Has one right angle and two acute angles.

By studying these properties, students can gain a deeper understanding of how triangles function within the broader context of geometry. Mastery of these concepts is key to solving problems involving angle relationships, side lengths, and area calculations.

Geometry Chapter 4: Quadrilaterals and Polygons

This section delves into the study of four-sided figures and multi-sided shapes, which play a significant role in understanding spatial relationships. By examining the characteristics and properties of these figures, students can develop skills to solve a wide range of problems, from calculating angles to determining areas. Understanding the different types of quadrilaterals and polygons is essential for tackling more complex geometric tasks.

Quadrilaterals, which are four-sided figures, and polygons, which can have many sides, each have distinct properties that help identify and classify them. These shapes are fundamental for understanding symmetry, area, and perimeter calculations, as well as for analyzing how shapes fit together in various geometric patterns.

Key Properties of Quadrilaterals

• Squares: All sides are equal, and all angles are 90°.
• Rectangles: Opposite sides are equal, and all angles are 90°.
• Parallelograms: Opposite sides are parallel and equal in length.
• Trapezoids: One pair of opposite sides are parallel.

Understanding Polygons

• Triangles: Three sides and three angles, with various types such as equilateral, isosceles, and scalene.
• Pentagons: Five sides and angles, often found in various real-world structures.
• Hexagons: Six sides, frequently seen in nature, such as in honeycomb patterns.
• Heptagons and Beyond: Polygons with seven or more sides, which can be used in more complex geometric designs.

By understanding the unique properties of quadrilaterals and polygons, students can approach more challenging geometric problems with confidence, whether they involve angle measurement, area calculation, or shape classification.

Understanding Circles in Geometry

A circle is a unique shape that appears in many areas of mathematics, engineering, and nature. It is defined by a set of points that are equidistant from a fixed center. Understanding the properties of circles is crucial, as they serve as the foundation for solving many problems involving angles, tangents, and arc lengths. By exploring the key characteristics of circles, students can build a deeper understanding of how this shape interacts with other geometric figures.

The circle’s fundamental properties–such as radius, diameter, circumference, and center–are vital for analyzing various aspects of circular motion and spatial relationships. By learning how to apply these concepts, one can approach problems related to areas, angles, and even real-world applications such as design and architecture.

Key Concepts of a Circle

• Radius: The distance from the center of the circle to any point on the circle.
• Diameter: A straight line passing through the center of the circle, with both ends touching the circle. The diameter is twice the length of the radius.
• Circumference: The total distance around the circle, calculated using the formula C = 2πr.
• Pi (π): A constant used to relate the circumference to the diameter, approximately 3.14159.

Circle Properties in Practice

• Angles: Angles formed by radii and chords within a circle, such as central and inscribed angles.
• Tangents: A line that touches the circle at exactly one point, which has specific properties in relation to the radius.
• Arcs: A portion of the circumference, often used in angle measurements or determining sector areas.

By mastering the properties and theorems related to circles, students can solve a wide range of problems, from calculating the area of circular regions to understanding more advanced concepts such as sector areas and segment lengths. This knowledge is not only foundational in mathematics but also applicable in fields like physics, engineering, and design.

Working with Geometric Transformations

In this section, we explore the concept of manipulating shapes through various operations that alter their position, size, and orientation. These operations, known as transformations, are fundamental tools in geometry, used to study the symmetry, congruence, and similarity of figures. Understanding how to apply transformations allows students to visualize the movement of shapes in a plane and solve problems related to symmetry and spatial relationships.

There are several key types of transformations, each with its own unique properties and applications. These operations include shifting, rotating, reflecting, and resizing shapes. By mastering these concepts, one can approach problems involving symmetry, coordinate geometry, and even real-world design challenges with greater confidence.

Types of Transformations

• Translation: Moving a shape from one location to another without altering its orientation or size. Every point of the figure moves the same distance and in the same direction.
• Rotation: Turning a shape around a fixed point, called the center of rotation. The angle of rotation determines how far the shape is turned.
• Reflection: Flipping a shape over a line of reflection, creating a mirror image. This transformation preserves the shape’s size but changes its orientation.
• Dilation: Resizing a shape by a certain scale factor, either enlarging or reducing the figure. This transformation affects the shape’s size but not its proportions.

Applications of Transformations

• Symmetry: Transformations help identify symmetrical properties in shapes, which is useful in design, architecture, and art.
• Coordinate Geometry: Transformations are essential in analyzing shapes in the coordinate plane, helping to solve problems related to distances, angles, and areas.
• Real-World Uses: From computer graphics to engineering, transformations play a critical role in modeling and designing various objects and systems.

By understanding and applying these transformations, students can deepen their comprehension of shapes and their relationships in the plane. This knowledge is vital for progressing to more advanced concepts in mathematics and its applications in the real world.

Using Geometry Proofs in Chapter Answers

In geometry, proving statements through logical reasoning is essential for establishing the validity of mathematical concepts. This process, known as a proof, involves a series of steps that demonstrate the truth of a particular claim based on previously established principles and axioms. Mastering the art of proof writing is crucial for solving problems, as it allows students to substantiate their conclusions and gain a deeper understanding of geometric relationships.

When working through exercises, students often encounter problems that require the use of proofs to justify their solutions. These problems test not only the ability to apply formulas and theorems but also the capacity to construct logical arguments. By carefully following the steps of a proof, one can deduce the required outcomes with clarity and precision. Whether proving the properties of triangles, angles, or more complex figures, understanding the structure of a proof is key to succeeding in geometry.

Key Elements of a Proof

• Given Information: The facts or conditions provided in the problem that serve as the foundation for the proof.
• Prove Statement: The assertion or claim that needs to be demonstrated as true using logical steps.
• Logical Steps: A series of reasoning steps that connect the given information to the prove statement, using definitions, postulates, and previously proven theorems.
• Conclusion: The final result of the proof, showing that the prove statement is indeed true based on the logical steps taken.

Applications of Proofs in Problem Solving

• Proving Congruence: Establishing that two shapes are identical in size and shape by showing that their corresponding parts match.
• Angle Relationships: Using proofs to demonstrate the relationships between angles formed by intersecting lines, parallel lines, and other geometric configurations.
• Area and Perimeter Calculations: Justifying the use of certain formulas and methods to calculate the area and perimeter of various figures.

By learning how to write and understand proofs, students gain the ability to tackle more advanced problems and develop critical thinking skills that will be useful in higher-level mathematics and beyond. Proofs not only help confirm the accuracy of answers but also reinforce the principles that govern geometric figures, enhancing overall mathematical reasoning.

Geometry Word Problems and Strategies

Word problems in mathematics are designed to assess the ability to translate real-life situations into mathematical expressions and solve them. These problems often involve geometric concepts such as shapes, angles, and measurements, requiring the application of appropriate formulas and logical reasoning. Effectively solving these problems demands not only understanding the theory behind geometric principles but also the skill to interpret and structure the given information correctly.

To solve these types of problems efficiently, it is important to develop a systematic approach. Identifying key elements in the problem, selecting the right formula or concept, and organizing the work step-by-step are all vital strategies. Whether dealing with perimeter, area, volume, or angles, following a structured method can help simplify complex problems and lead to accurate solutions.

Step-by-Step Approach to Solving Problems

• Read Carefully: Understand the problem by identifying all the given information and what needs to be found.
• Draw Diagrams: Visualize the problem by sketching shapes and labeling important details. This can make it easier to identify relationships and apply the right principles.
• Choose the Right Formula: Select the most appropriate mathematical formulas or theorems based on the information provided.
• Work Step-by-Step: Break the problem down into manageable steps, ensuring each step logically follows from the previous one.
• Check Your Answer: Verify that the solution makes sense in the context of the problem and review the calculations for accuracy.

Common Problem Types and Solutions

• Perimeter and Area: These problems typically involve finding the lengths of sides or the area of two-dimensional shapes. Apply appropriate formulas based on the shape, such as the perimeter of a rectangle or the area of a triangle.
• Volume and Surface Area: In three-dimensional problems, determining the volume or surface area of solids like cubes, spheres, and cylinders is common. Use formulas like V = πr²h for cylinders or V = lwh for rectangular prisms.
• Angle Problems: Often, problems will involve finding unknown angles using properties such as complementary, supplementary, or vertical angles. Remember to apply angle rules to solve these types of questions.

Mastering the strategies for solving word problems is essential for not only performing well in geometry but also for applying mathematical thinking to real-world situations. By following a systematic approach, students can improve their problem-solving skills and confidently tackle increasingly complex challenges.

Geometry Chapter Review and Practice

Reviewing and practicing key concepts in mathematics is essential for reinforcing understanding and improving problem-solving skills. This process allows students to consolidate their knowledge, identify areas that need improvement, and become more confident in applying geometric principles. Regular practice, paired with thorough review, enhances the ability to tackle various types of problems efficiently and accurately.

In this section, we will focus on strategies for reviewing the main ideas covered in previous lessons and offer practical exercises to test your skills. These activities are designed to solidify understanding of core topics, such as shapes, angles, and measurement. By engaging in these practice problems, you can refine your skills and prepare for more advanced topics.

Key Review Strategies

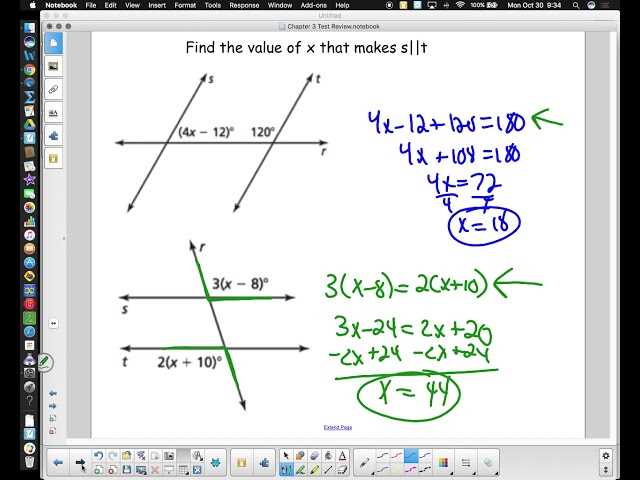
• Summarize Key Points: Write down a summary of the most important concepts from the lesson. This will help reinforce your understanding and serve as a quick reference guide.
• Practice Problems: Solve a variety of problems related to the topic. Begin with simpler examples and gradually increase the complexity as you feel more confident.
• Work in Groups: Discussing problems with peers can provide different perspectives and lead to a deeper understanding of difficult concepts.
• Use Visual Aids: Diagrams, charts, and models can help visualize geometric relationships and make abstract ideas more concrete.

Types of Practice Exercises

• Multiple Choice Questions: These are useful for testing quick recall of facts, formulas, and definitions.
• Word Problems: Real-life scenarios challenge your ability to apply geometric concepts in practical situations.
• Proofs and Theorems: Practice constructing logical arguments and applying geometric properties to prove statements.
• Hands-On Activities: Use manipulatives or drawing tools to create shapes and explore their properties interactively.

By integrating review and practice into your study routine, you can reinforce the material and build a stronger foundation for future mathematical learning. Regular exercises help not only with retention but also with the confidence needed to approach new challenges successfully.

How to Prepare for Geometry Tests

Preparing for an assessment in mathematics requires focused study, strategic planning, and consistent practice. The key to doing well on tests is not just memorizing formulas, but also understanding the underlying principles and being able to apply them to solve a variety of problems. By following effective preparation techniques, you can improve your chances of success and reduce test-day anxiety.

Here are some helpful steps to take when preparing for a test in mathematics:

Effective Study Methods

• Review Class Notes and Textbooks: Go over your notes and textbooks regularly to make sure you have covered all the necessary topics. Pay attention to important definitions, theorems, and problem-solving strategies.
• Practice Regularly: Work on a variety of problems that cover different concepts. Regular practice helps solidify your understanding and makes you more confident in applying your knowledge to new problems.
• Understand Mistakes: When you make an error, take the time to understand why. Reviewing mistakes will help you avoid them in the future and deepen your understanding of the material.
• Use Flashcards: Create flashcards for key formulas, definitions, and theorems. These can be easily reviewed on-the-go and help reinforce your memory.

Test-Taking Strategies

• Time Management: During your preparation, practice managing your time effectively. When taking the test, pace yourself so that you have enough time to answer all questions, even the more challenging ones.
• Start with What You Know: Begin by tackling the questions you feel most confident about. This will build momentum and boost your confidence for more difficult problems.
• Check Your Work: If time allows, review your answers to ensure that you have completed all steps and haven’t missed anything important. Small mistakes can often be overlooked in a rush.
• Stay Calm: Staying calm during the test will help you think clearly and work more efficiently. Deep breaths and positive thinking can reduce test anxiety.

By incorporating these preparation and test-taking strategies, you will be better equipped to handle a variety of questions and succeed in your assessment. Regular study, consistent practice, and a calm approach to the test will all contribute to achieving your best results.

Geometry Resources for Advanced Learners

For those seeking to deepen their understanding and mastery of mathematical concepts, there are a variety of specialized materials designed to challenge and enhance knowledge. These tools offer more complex problems, theoretical explanations, and opportunities to explore topics at a higher level. Advanced learners can benefit from resources that encourage independent problem-solving, critical thinking, and the exploration of more sophisticated mathematical principles.

Books and Texts for In-Depth Study

Advanced students can explore a range of specialized books that offer detailed explanations and complex problems. These texts dive deeper into mathematical theories, proofs, and advanced topics not always covered in introductory coursework. A few recommended options include:

• Advanced Euclidean Geometry: This book focuses on deeper theorems, offering insights into classical geometric concepts with a modern twist.
• Mathematical Methods in the Physical Sciences: A text that combines mathematical theories with practical applications, often used by those pursuing higher studies in science and engineering.
• Problems in Mathematics: A collection of challenging problems designed for advanced learners, often including solutions and hints to encourage critical thinking.

Online Platforms for Exploration

In addition to books, there are numerous online platforms and forums where advanced learners can expand their knowledge and connect with others. These platforms offer problem sets, interactive lessons, and opportunities for peer discussion:

• Art of Problem Solving (AoPS): AoPS offers a range of challenging problems and online courses, perfect for students who want to push their understanding of advanced mathematical concepts.
• Khan Academy (Advanced Math Section): While Khan Academy is known for its introductory content, it also offers more advanced lessons in mathematics, including calculus and linear algebra.
• Brilliant.org: Brilliant’s interactive problem-solving courses are excellent for deepening knowledge in both theoretical and applied mathematics, including geometry and other advanced topics.

By using a combination of textbooks and online platforms, advanced learners can explore higher-level mathematical concepts, challenge themselves with more complex problems, and gain a deeper understanding of the subject. These resources offer opportunities for independent exploration and mastery, preparing students for further study or competitive exams.

Additional Online Tools for Geometry Study

In today’s digital age, a variety of online tools can enhance the study of mathematical concepts, providing interactive experiences, visual aids, and customizable problem sets. These platforms support students by offering unique ways to visualize and practice different aspects of mathematics, fostering a deeper understanding of complex topics. Whether you’re solving problems, exploring geometric shapes, or experimenting with equations, these tools can be valuable assets to any student’s learning journey.

Interactive Geometry Platforms

Several websites and applications offer interactive tools that allow users to experiment with geometric shapes, angles, and transformations. These platforms provide hands-on experience, allowing students to manipulate objects and explore mathematical principles in a visual and intuitive way.

Platform	Features	Best For
GeoGebra	Interactive graphing tools, geometry construction, and algebraic operations	Visual learners and those practicing geometry constructions
Desmos	Graphing calculator with geometric visualization and dynamic graphs	Students working on coordinate geometry and graphing
WolframAlpha	Mathematical computation engine with step-by-step solutions	Students seeking quick answers and explanations for complex problems

Tools for Visualizing Concepts and Theorems

Understanding theorems and proofs is often easier when concepts are visualized. Some online tools are specifically designed to help students explore geometric principles through visual aids and animations, allowing them to see the relationship between different components of a figure.

Tool	Features	Best For
Geometry Pad	Build and manipulate geometric shapes to explore properties and relationships	Students practicing geometric proofs and constructions
Sketchpad	Interactive platform for creating and exploring mathematical models	Students visualizing and experimenting with geometric shapes
Geometer’s Sketchpad	Tools for constructing and analyzing geometric shapes with precision	Students who need to visualize complex geometric transformations

By incorporating these online tools into study routines, students can gain a more interactive and engaging learning experience. These platforms provide essential support, from solving problems to understanding abstract concepts, making them indispensable for students of all levels. Whether you’re preparing for tests or simply looking to explore new concepts, these tools will provide the necessary resources to deepen your understanding and improve your problem-solving skills.