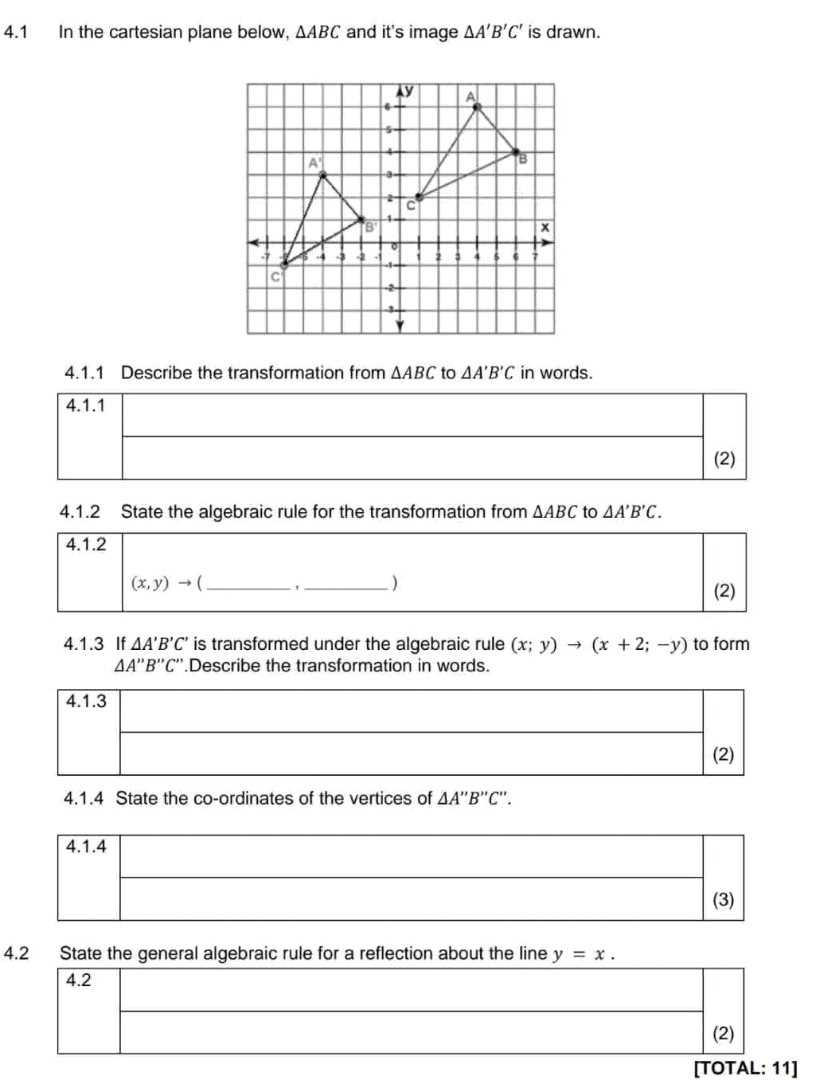
4.1.1 Answer Key Solutions and Explanations
Understanding complex exercises or tasks often requires a detailed explanation of the correct solutions. This section provides a comprehensive guide to help clarify key concepts and ensure a full grasp of the material. By breaking down each problem, you will gain insight into the reasoning behind the answers and improve your understanding of the subject matter.
Learning from provided solutions offers a deeper comprehension of how to approach similar challenges in the future. The detailed breakdown allows you to not only check your work but also learn the steps that lead to accurate results. Through this method, you can enhance both your skills and your confidence in tackling future problems.
In addition, identifying and correcting mistakes plays a critical role in mastering any topic. This guide will assist you in recognizing common pitfalls and understanding why certain answers are incorrect, allowing you to avoid them in subsequent tasks.
1 Solution Overview
In this section, we will provide an in-depth look at the provided solutions for the exercises. The goal is to help users better understand the rationale behind each correct response and the methodology for reaching the most accurate conclusions. A detailed approach is taken to ensure clarity in solving various problems, and this will serve as a useful reference for those working through similar tasks.
The guide emphasizes key strategies, such as:
- Breaking down each problem into manageable steps
- Identifying common challenges and how to avoid them
- Providing context for the logic behind each solution
By carefully examining the solution approach, learners will be able to recognize patterns, grasp underlying concepts, and apply these techniques effectively in future work. This section also helps build problem-solving skills that go beyond simply finding the right answers.
Overall, the focus is on building a strong foundation of knowledge and fostering a deeper understanding of the subject matter. By mastering these approaches, individuals can confidently navigate complex tasks and develop a strategic mindset for tackling problems.
Understanding the Questions
Grasping the core elements of each question is essential for finding the correct solutions. This section focuses on how to interpret and approach various types of problems, highlighting key aspects that are often overlooked. A clear understanding of the underlying principles will help ensure that you’re tackling each problem from the right perspective.
Key Areas to Focus On
- Identifying the main objectives of the question
- Breaking down complex statements into simpler components
- Recognizing any assumptions or constraints that influence the solution
Many questions require careful consideration of all elements before jumping into solving them. Understanding the context and any underlying conditions is crucial in ensuring a precise response. By taking the time to analyze each part, you can avoid common errors and apply the correct methods for reaching your conclusions.
Common Pitfalls to Avoid
- Rushing through the problem without full comprehension
- Overlooking key details that may affect the outcome
- Failing to recognize patterns that simplify the solution process
By recognizing these common pitfalls and focusing on the critical elements, you’ll improve your ability to understand the core of each problem and successfully navigate through the solution process.
How to Use the Solution Guide

Effectively utilizing a solution guide involves more than just comparing results. It’s a tool designed to help you understand the process behind each correct outcome. Instead of simply checking if your response matches, focus on learning the steps that lead to the solution. This approach will enhance your problem-solving abilities and deepen your comprehension of the material.
Start by reviewing the provided steps carefully. Try to follow each one in sequence, paying attention to the logic and reasoning behind each action. If you find any discrepancies between your approach and the guide, take time to understand why. This analysis will help you identify areas where you can improve your technique.
Additionally, using the solution guide as a reference for practice is crucial. Rather than relying solely on it for verification, challenge yourself to work through problems independently and only consult the guide when you encounter difficulties. This strategy promotes active learning and ensures you are gaining the skills needed to solve problems without assistance.
Common Mistakes in Solution Approaches
When working through problems, it’s easy to make mistakes that can lead to incorrect results. Identifying these common errors is crucial for improving accuracy and mastering the material. Many of these mistakes stem from misunderstandings of the question, misinterpretation of steps, or overlooking key details. Being aware of these pitfalls allows you to avoid them and develop more effective problem-solving strategies.
One common mistake is failing to fully understand the problem before attempting a solution. Rushing through the process without carefully reading the instructions often leads to overlooking important aspects of the task. This can result in errors that could have been easily avoided with a more thoughtful approach.
Another frequent issue is skipping intermediate steps. While it might seem faster to jump ahead, skipping crucial steps can result in missing out on vital concepts. This often leads to a solution that appears correct at first glance but is flawed when examined in more detail.
Lastly, many individuals make the mistake of not double-checking their work. After completing a solution, it’s important to review each step to ensure accuracy. Mistakes can go unnoticed if no effort is made to verify the correctness of each action taken during the process.
Tips for Accurate Solutions
Achieving precise results requires more than just following steps–it demands a methodical approach, attention to detail, and a deep understanding of the problem at hand. This section offers practical strategies to improve the accuracy of your solutions. By refining your approach and focusing on key principles, you can avoid common errors and enhance your problem-solving efficiency.
Thoroughly Understand the Problem
Before jumping into solving any problem, take the time to fully comprehend what is being asked. Rushing through the problem statement can lead to overlooking essential details. Carefully identify the main objectives and the constraints provided, as they will guide your approach to finding the correct solution.
Check Your Work Step by Step
One of the best ways to ensure accuracy is to verify each step as you progress. This approach helps catch mistakes early before they compound into larger issues. After completing the solution, go back and review each part to ensure that the logic is sound and all necessary steps have been followed correctly.
Additionally, don’t hesitate to approach the problem from multiple angles. Sometimes, rethinking a solution method can reveal simpler or more accurate ways to reach the desired outcome. This reflective process promotes a deeper understanding of the material and reinforces good problem-solving habits.
Why Accurate Solutions Matter
Providing correct responses to problems is not just about getting the right result–it’s about demonstrating a thorough understanding of the underlying principles. The importance of accurate solutions extends beyond merely passing a task or test; it reflects a deeper comprehension of the material and helps build the skills necessary for more complex challenges.
Correct results provide several key benefits:
- They confirm your grasp of essential concepts and methods.
- They serve as a foundation for more advanced problem-solving techniques.
- They reveal patterns and strategies that can be applied in future tasks.
When you consistently arrive at the right solutions, it builds your confidence and reinforces your ability to approach new problems with a structured mindset. This makes learning more efficient and ensures that you can adapt to a variety of challenges as they arise. Ultimately, accurate results are the stepping stones to mastering any subject and advancing in any field.
Exploring Key Concepts in Solutions
Understanding the core principles behind the correct methods is crucial for mastering any subject. This section delves into the fundamental concepts that drive the reasoning behind each solution. By breaking down these key ideas, you will be able to apply them to a variety of problems, enhancing your overall problem-solving ability and comprehension.
Core Principles to Master
Several key ideas are integral to approaching problems accurately. These concepts provide the foundation for understanding how different elements interact and contribute to the final solution. Here are some of the most important principles to keep in mind:
| Concept | Description |
|---|---|
| Problem Breakdown | Dividing complex issues into smaller, manageable parts for better clarity and focus. |
| Step-by-Step Logic | Applying systematic reasoning to ensure each stage of the process is correct. |
| Consistency in Method | Following a consistent approach across similar problems for reliable results. |
| Attention to Detail | Ensuring that no important elements are overlooked, which could affect the outcome. |
Applying These Concepts
Once the key principles are understood, it’s important to practice applying them in real-world scenarios. By recognizing how these concepts work together, you can streamline your problem-solving process and approach each challenge with greater confidence. The more you apply these foundational ideas, the more intuitive your ability to tackle complex problems will become.
Step-by-Step Guide to Solving Problems

Breaking down a complex problem into manageable steps is essential for ensuring accuracy and clarity in finding the solution. This guide offers a structured approach to tackle any problem, allowing you to follow each stage systematically. By following this process, you can minimize errors and improve your overall problem-solving efficiency.
The following steps outline the process to solve problems effectively:
| Step | Action | Purpose |
|---|---|---|
| Step 1 | Understand the Problem | Read and interpret the problem carefully, identifying key objectives and constraints. |
| Step 2 | Break It Down | Divide the problem into smaller, manageable parts to simplify the approach. |
| Step 3 | Choose the Right Method | Select the most suitable approach or strategy based on the problem’s requirements. |
| Step 4 | Work Through the Solution | Follow the chosen method step-by-step, applying logical reasoning at each stage. |
| Step 5 | Verify Your Work | Review your solution to ensure all steps were followed correctly and the result is accurate. |
By adhering to these steps, you can approach problems with confidence and clarity, ensuring that each solution is both accurate and well-understood. Each step is designed to build upon the last, creating a logical flow that minimizes the risk of errors and helps reinforce the problem-solving process.
Understanding Solution Breakdown
Breaking down a solution into smaller, manageable components is essential for gaining a deeper understanding of the problem-solving process. By examining each part individually, you can identify how different elements contribute to the overall outcome. This approach not only helps clarify the reasoning behind each decision but also improves your ability to apply similar methods to future problems.
In any complex task, it’s important to follow a structured breakdown. This typically involves recognizing key stages and understanding how they connect to one another. Here’s how you can break down a solution effectively:
- Identify the Problem: Understand the overall goal and what needs to be solved. This is the foundation of any solution.
- Analyze the Given Information: Gather and assess all available data or conditions that must be considered in the solution.
- Determine Necessary Steps: Outline the logical steps required to move from the starting point to the solution, ensuring nothing is overlooked.
- Work Through Each Step: Apply the necessary techniques or formulas, step by step, to arrive at a partial solution.
- Verify the Process: Ensure each step logically follows from the previous one and contributes correctly toward the final answer.
By following these stages, the problem-solving process becomes more manageable, and the connections between each part of the solution become clearer. This not only ensures accuracy but also strengthens your understanding of the methods used, which is essential for mastering complex tasks.
1 Solution Examples
Providing real-world examples of how to approach problems can help clarify the process and solidify your understanding of effective methods. By exploring practical cases, you can better understand how each component fits together to create a complete solution. In this section, we will review a variety of examples to demonstrate how to apply structured thinking to solve challenges successfully.
Example 1: Simple Calculation
Consider a simple mathematical problem where you are asked to calculate the total cost of items given their individual prices and quantities. Here’s how the solution breaks down:
- Step 1: Identify the prices and quantities of the items.
- Step 2: Multiply the price by the quantity for each item.
- Step 3: Add the results to get the total cost.
- Step 4: Verify the total sum to ensure the calculation is correct.
By following this straightforward process, the solution becomes clear and easy to verify, reinforcing the importance of systematic steps.
Example 2: Logical Reasoning Problem
In a logic puzzle, you may be asked to determine the correct order of events based on a set of clues. Here’s a breakdown of how to approach it:
- Step 1: Review all the given clues carefully.
- Step 2: Create possible scenarios or sequences based on the information.
- Step 3: Eliminate inconsistencies and narrow down the options.
- Step 4: Verify the final order by cross-checking against the clues.
This example highlights how organizing information and eliminating wrong answers can lead to a correct solution, showing the importance of a methodical approach in logical reasoning.
Checking Your Solutions Effectively

Reviewing your work is a crucial step in the problem-solving process. By carefully examining each step and result, you can ensure accuracy and catch any errors before finalizing the solution. A systematic approach to verification helps confirm that the logic, calculations, or reasoning used are correct, preventing unnecessary mistakes. This section will explore strategies to check your work effectively, ensuring a thorough and reliable outcome.
Step 1: Revisit Each Step
Start by going over every stage of the process to confirm that all operations were completed correctly. Ensure that no detail was overlooked or misinterpreted. This approach provides a clear path to trace potential sources of error and correct them promptly.
- Review Input Data: Verify that the initial information is accurate and appropriately used.
- Recalculate Where Necessary: Double-check any numerical operations, ensuring proper handling of arithmetic and formulas.
- Examine Assumptions: Reassess the assumptions made during the solution process to ensure they are still valid.
Step 2: Cross-Check with Alternative Methods
If possible, use different methods to solve the same problem. Comparing results from alternative approaches can help spot inconsistencies and confirm the accuracy of your solution. This step is particularly useful for complex problems where multiple strategies may yield the same or different results.
- Use Visual Aids: Diagrams, graphs, or charts can provide clarity and make it easier to identify any discrepancies.
- Consult Reliable Sources: If unsure, check reference materials or previous examples to see if your solution aligns with established methods.
By following these steps, you can ensure that your results are not only correct but also supported by logical reasoning and verification. This process reinforces the integrity of your work and provides confidence in your conclusions.
Using the Solution Guide for Practice

Using a solution guide can be a valuable resource for reinforcing learning and improving problem-solving skills. By reviewing the steps provided in a guide, you can better understand the logic behind each decision and learn how to apply similar strategies to new problems. This practice not only enhances your understanding but also helps build confidence in your ability to tackle similar tasks independently.
When using a solution guide for practice, it’s essential to focus on the process rather than just the final outcome. Here are some strategies for making the most of this tool:
- Analyze Each Step: Carefully review the methodology used in the guide. Understand why each step was taken and how it contributes to the solution.
- Compare with Your Attempts: After attempting a problem on your own, compare your approach with the guide’s solution. Identify any differences and learn from them.
- Practice Similar Problems: Use the guide as a reference and try solving similar problems without immediately looking at the solution. This helps reinforce learning and builds problem-solving confidence.
By regularly using the solution guide for practice, you will improve your ability to approach complex problems, build your reasoning skills, and increase your overall performance in similar tasks.
Why Some Solutions Are Incorrect
There are various reasons why solutions to problems may not be accurate, even when the process seems to have been followed correctly. Errors can stem from misunderstandings of the task, incorrect assumptions, or miscalculations. Identifying these issues is essential for improving problem-solving skills and ensuring more accurate outcomes in the future.
Common causes of incorrect results include:
- Misinterpretation of the Problem: A common reason for an incorrect solution is misunderstanding the question or the parameters of the problem. This can lead to applying the wrong method or focusing on irrelevant details.
- Incorrect Assumptions: Often, solutions are based on assumptions that may not hold true, leading to flawed conclusions. It’s important to verify assumptions before proceeding with a solution.
- Calculation Errors: Simple arithmetic mistakes or incorrect application of formulas can result in wrong results, even if the rest of the process is followed correctly.
- Overlooking Key Details: Missing or neglecting important information, such as units of measurement or specific instructions, can easily lead to inaccurate results.
By recognizing and addressing these common mistakes, you can significantly reduce the likelihood of errors and improve the accuracy of your solutions in future problems.
Comparing Different Solution Approaches
When tackling complex problems, multiple strategies can lead to different outcomes. Understanding these various approaches is key to selecting the most effective method for a given task. By comparing different solution strategies, you can gain insight into how diverse methods affect the result and learn how to adapt your approach for similar future challenges.
In this section, we explore how different problem-solving approaches can be applied to the same task, highlighting their strengths and potential drawbacks. By examining each method, you can determine which one suits your needs the best based on efficiency, accuracy, and ease of application.
Approach 1: Step-by-Step Calculation
This method involves carefully following a set of instructions or procedures to break down a task into smaller, manageable parts. It is often used for problems that have a clear and structured solution path. However, this approach may be time-consuming and may overlook alternative, quicker methods.
Approach 2: Intuitive Guesswork
In contrast, this approach relies on intuition or estimation to arrive at a solution quickly, sometimes without fully analyzing the problem. While it can be effective in situations requiring rapid decision-making, it is prone to errors and may not always lead to the most accurate results.
| Approach | Advantages | Disadvantages |
|---|---|---|
| Step-by-Step Calculation | Clear structure, systematic, thorough | Time-consuming, may overlook shortcuts |
| Intuitive Guesswork | Fast, effective in urgent situations | Risk of inaccuracies, less reliable |
By comparing these two approaches, it’s clear that each has its advantages and is suited to different types of problems. For more complex or high-stakes tasks, a detailed, methodical approach may be necessary, while quicker tasks may benefit from intuitive methods. The key is to understand when to apply each approach based on the situation at hand.
Learning from Mistakes

Mistakes are an essential part of the learning process, offering valuable lessons that can help us improve. In problem-solving, errors often point to gaps in understanding or missteps in approach. By analyzing these mistakes carefully, we can identify what went wrong and how to avoid repeating them in the future. This section focuses on the importance of recognizing and learning from errors in any task.
When facing challenges, mistakes can offer insights that lead to better strategies and techniques. It’s crucial not only to acknowledge errors but also to understand their root causes. Through this understanding, individuals can refine their methods and increase the likelihood of achieving accurate results in future attempts.
Common Mistakes to Avoid
- Skipping Steps: Rushing through tasks without thoroughly considering each stage can lead to incomplete or incorrect results.
- Overcomplicating Solutions: Trying to apply overly complex methods when simpler approaches would suffice can waste time and introduce errors.
- Misinterpreting Information: Failing to correctly analyze or interpret key details often leads to wrong conclusions and mistakes in execution.
How to Learn from Errors
- Review and Reflect: After identifying a mistake, take the time to thoroughly review your approach and the reasoning behind your decisions.
- Identify Patterns: Look for recurring themes in your errors to help you understand if there are consistent gaps in knowledge or application.
- Adapt and Adjust: Use the lessons learned from mistakes to adjust your approach in the future, ensuring that similar errors are avoided.
By transforming mistakes into learning opportunities, individuals can continuously refine their skills and increase their effectiveness. Instead of viewing errors as setbacks, embrace them as tools for growth and improvement.
Strategies to Master Problem-Solving
Mastering any subject or task requires a structured approach and consistent effort. By implementing effective strategies, learners can not only understand the material better but also solve problems with greater accuracy and confidence. This section outlines key methods to help improve your skills and increase your chances of success.
To become proficient, it’s essential to approach learning systematically. Breaking down complex tasks into manageable steps, reviewing past mistakes, and practicing regularly are all vital strategies. Additionally, developing a deeper understanding of fundamental concepts allows you to solve problems more effectively and with less frustration.
Key Techniques for Mastery
- Consistent Practice: Regular practice is crucial. Set aside time each day to work through problems and reinforce your knowledge.
- Break Down Complex Problems: Tackle complicated challenges step by step, ensuring each part is understood before moving to the next.
- Seek Clarification: When a concept or problem is unclear, don’t hesitate to ask for help. Seeking clarification early prevents misunderstandings from compounding later.
- Review and Reflect: After completing tasks, take the time to review your work. Identify areas of weakness and understand where you went wrong.
Building Confidence Through Practice
One of the most effective ways to master any skill is through repetition and feedback. As you progress, you’ll build confidence in your ability to tackle new challenges. Keep challenging yourself with more complex problems, and use mistakes as learning opportunities to improve your approach. Over time, you’ll develop both the knowledge and the confidence needed to excel in any subject area.
Frequently Asked Questions about Problem-Solving
This section aims to address common questions that learners may have when navigating challenges and seeking solutions. Understanding key concepts and approaches can help clarify confusion and offer useful insights for better performance. Below are answers to some of the most frequently asked questions regarding problem-solving techniques and strategies.
What is the best way to approach difficult problems?
The best way to tackle challenging tasks is to break them down into smaller, more manageable steps. Start by identifying the core components of the problem, and then address each one individually. This approach allows you to focus on one part at a time, reducing the overwhelming feeling that can come with complex problems.
How can I improve my problem-solving skills?
Improvement comes with consistent practice. Regularly solving a variety of problems helps develop critical thinking and analytical skills. It is also important to reflect on previous mistakes, as learning from errors enhances understanding and prevents similar issues in the future.
Why do I sometimes get answers wrong even after studying?

It’s common to make mistakes, especially when encountering unfamiliar problems. Factors like stress, misunderstanding key concepts, or rushing through a solution can lead to errors. The key is to focus on the learning process, and not just the results, as each mistake provides valuable feedback that helps refine your skills.
Is there a way to verify my solutions effectively?
Yes, verifying solutions can be done by double-checking your steps and reasoning. If possible, compare your solution with others, whether through peer discussions or using reliable resources. Additionally, revisiting key concepts that relate to the problem can help ensure that your solution is grounded in the correct logic.