Algebra Nation Section 7 Answers Explained

In this part of your learning journey, you’ll encounter a variety of problems designed to test your skills and deepen your understanding of mathematical principles. The focus is on applying different techniques to solve equations and tackle challenges that require both logic and critical thinking.
Mastering these exercises will not only strengthen your mathematical knowledge but also enhance your ability to approach problems methodically. Each question provides an opportunity to practice essential concepts that are foundational for higher-level math studies.
As you progress through these tasks, you’ll uncover strategies that make complex problems more manageable. The goal is to develop a thorough understanding, enabling you to confidently handle similar problems in the future. By the end of this section, you’ll have a clearer grasp of how to approach different types of equations and real-world applications.
Mastering Key Math Concepts and Solutions
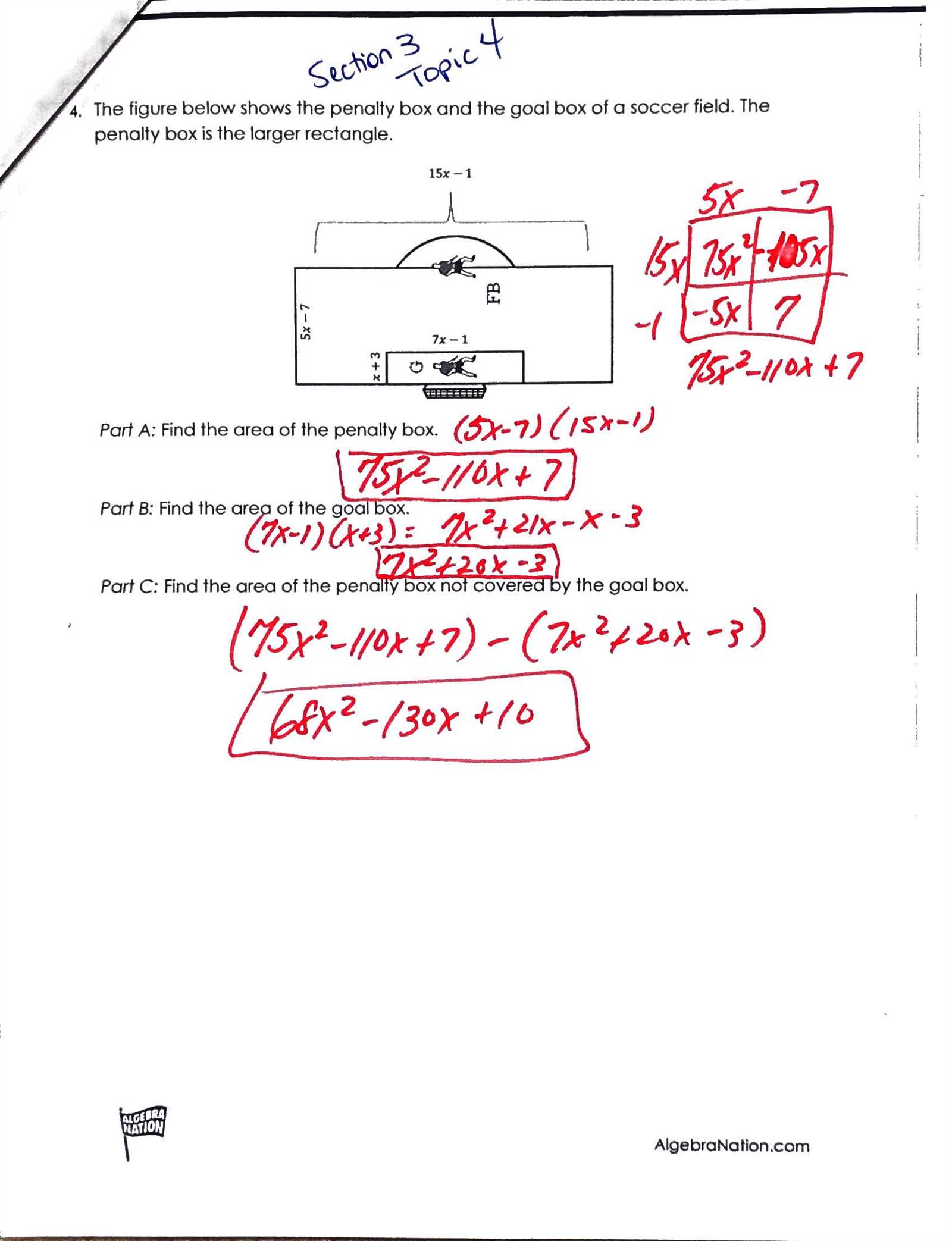
To master the challenges presented in this part of the curriculum, it’s essential to focus on understanding the core principles behind each problem. By approaching each exercise step by step, you can develop a deeper comprehension of how to break down complex tasks into manageable components. Success in these exercises requires a blend of logical thinking, practice, and familiarity with the methods that work best for solving equations.
Effective problem-solving techniques often involve recognizing patterns and applying learned strategies. One key to mastering these exercises is being consistent with your practice and not rushing through problems. It’s important to review each solution carefully and understand why certain approaches work better than others. By doing so, you’ll build confidence in your skills and be able to tackle increasingly difficult problems with ease.
Here’s a quick reference guide to help you stay on track as you work through the problems:
| Step | Description |
|---|---|
| 1 | Read the problem carefully and identify the key information. |
| 2 | Break the problem down into smaller, more manageable parts. |
| 3 | Apply the appropriate mathematical method or formula. |
| 4 | Double-check the solution for accuracy and clarity. |
| 5 | Review the concepts to ensure understanding before moving on. |
By following these steps and focusing on consistent practice, you’ll be able to master the concepts and feel confident in solving similar challenges in the future.
Understanding Key Concepts in Section 7
This section introduces important mathematical ideas that are fundamental for solving a variety of problems. Mastery of these concepts is crucial for tackling more advanced topics and building a solid foundation for future studies. By breaking down the ideas into smaller, digestible parts, you can better understand how each concept fits into the broader picture of mathematics.
Core Principles to Focus On
- Recognizing patterns in equations
- Understanding relationships between variables
- Mastering key formulas and techniques
- Applying logical reasoning to solve problems
- Building confidence in mathematical methods
Focusing on these core principles will help you navigate through the challenges and reinforce your problem-solving skills. As you work through different exercises, you’ll begin to see how these concepts interconnect, making it easier to approach complex problems with confidence.
Steps for Grasping the Concepts
- Start by reading the problem carefully to identify key elements.
- Break down complex problems into simpler components.
- Apply the appropriate mathematical methods or operations.
- Review your work and understand the reasoning behind each step.
- Revisit any concepts that seem unclear and practice with additional examples.
By following these steps, you can ensure a deeper understanding of the material and improve your overall problem-solving ability. Regular practice is key to reinforcing the concepts and building your proficiency in mathematical techniques.
Step-by-Step Solutions for Section 7
To fully grasp the concepts in this part of the curriculum, it’s essential to approach each problem with a structured method. Breaking down each exercise into manageable steps allows for better understanding and greater accuracy. By following a clear, systematic approach, you’ll gain the skills necessary to confidently solve similar challenges in the future.
Step-by-Step Process for Solving Problems
- Read the problem carefully: Identify the key information and what the problem is asking.
- Organize the data: Write down any known values and variables clearly, and note the relationships between them.
- Choose the right method: Select the mathematical operation or technique that best fits the problem.
- Perform the calculations: Execute each step of the solution, showing all your work to avoid mistakes.
- Check your solution: Review the steps and ensure that your final result makes sense in the context of the problem.
Common Mistakes to Avoid
- Rushing through steps without double-checking your work.
- Forgetting to apply the correct formula or method.
- Misinterpreting the information provided in the problem.
- Skipping important steps in the solution process.
By following this step-by-step approach and avoiding common mistakes, you’ll be able to master the exercises and build a strong foundation for more advanced mathematical challenges.
Tips for Efficient Problem Solving
To solve mathematical problems more effectively, it’s important to streamline your approach and develop strategies that save time while ensuring accuracy. By following a few key techniques, you can improve both your speed and precision when working through exercises. These tips will help you approach challenges with confidence and consistency.
Key Strategies for Efficiency

- Understand the problem: Before you begin solving, ensure you fully understand the question and the information provided.
- Break it down: Split complex problems into smaller, simpler parts to avoid feeling overwhelmed.
- Choose the best method: Select the most efficient technique or formula that applies to the problem at hand.
- Double-check your work: Review your calculations as you go to catch potential mistakes early.
- Practice regularly: The more you practice, the quicker you will identify patterns and solve problems more efficiently.
Tools for Enhancing Problem-Solving Skills
| Tool | Purpose |
|---|---|
| Calculator | Helps with complex calculations and reduces errors. |
| Graphing Tools | Visualize equations and identify solutions more clearly. |
| Practice Sheets | Allows for repetitive practice and mastery of concepts. |
| Online Tutorials | Provide step-by-step instructions for understanding various methods. |
By integrating these strategies and tools into your study routine, you’ll be able to solve problems more efficiently and with greater ease.
Common Mistakes to Avoid in Algebra
When working through mathematical problems, it’s easy to make mistakes that can lead to incorrect solutions. Recognizing these common errors and knowing how to avoid them is key to improving your problem-solving skills. By being aware of these pitfalls, you can develop a more accurate and efficient approach to solving challenges.
Frequent Mistakes in Problem Solving
- Skipping steps: Rushing through problems without clearly writing down each step can result in missed calculations or overlooked details.
- Misunderstanding the question: Not fully understanding what is being asked can lead to applying the wrong methods or making incorrect assumptions.
- Forgetting to check work: Failing to review your solution can leave errors uncorrected, which can impact the final result.
- Overcomplicating simple problems: Trying to use advanced methods for basic problems often leads to unnecessary confusion and errors.
- Incorrect use of formulas: Misapplying mathematical formulas or using them in the wrong context is a common error that can skew results.
How to Avoid These Mistakes
- Take your time and review each step carefully.
- Always make sure you understand the problem before starting to solve it.
- Double-check your calculations and verify the logic behind each solution.
- Stick to simpler methods when possible, and avoid overcomplicating straightforward problems.
- Ensure you are using the correct formulas for the given problem.
By being mindful of these common mistakes and implementing strategies to avoid them, you can enhance your accuracy and efficiency when solving problems.
How to Approach Section 7 Questions
When tackling problems in this part of the curriculum, it’s important to develop a clear and structured approach. Each question presents a unique challenge, but with the right strategies, you can break them down into manageable tasks. By following a step-by-step method, you will be able to apply the correct techniques and reach solutions more confidently.
Step-by-Step Approach to Solving Problems

- Understand the question: Read the problem thoroughly to identify the key information and what is being asked.
- Organize your information: Write down the known values and variables, and clearly define the relationships between them.
- Select the appropriate method: Choose the right approach based on the type of problem–whether it’s solving an equation, finding a pattern, or applying a formula.
- Work through the problem: Perform the necessary calculations or operations step by step, showing all your work to avoid mistakes.
- Verify your solution: Check your final answer against the original question to ensure it makes sense and fits the context.
Common Strategies for Success
- Don’t rush: Take your time with each question, ensuring you understand each step before moving forward.
- Stay organized: Keep track of all your work and ensure clarity in your calculations.
- Use logical reasoning: Apply your understanding of mathematical principles to guide your approach to each problem.
- Practice regularly: The more you practice, the more intuitive problem-solving becomes, and the faster you’ll be able to recognize patterns and methods.
By following this structured approach and consistently practicing, you will gain a deeper understanding of how to handle different types of problems and improve your overall problem-solving skills.
Using Algebraic Methods to Solve Problems
Mathematical problem-solving often relies on specific techniques that help break down complex challenges into simpler steps. These methods involve manipulating variables and equations to find unknown values or relationships between different elements. By applying these strategies, you can solve problems with greater efficiency and accuracy.
Key Algebraic Techniques
- Solving Equations: This method involves isolating the variable to find its value. Whether you’re dealing with linear equations or more complex expressions, this approach is essential for finding solutions.
- Factoring: Breaking down complex expressions into simpler factors allows you to solve problems by finding common terms or roots.
- Substitution: Substituting known values into an equation helps reduce it to a simpler form, making it easier to solve.
- Combining Like Terms: This technique involves simplifying expressions by adding or subtracting terms with the same variables, making calculations quicker and clearer.
- Graphing: Visualizing equations on a coordinate plane can offer insights into the relationship between variables, allowing you to solve problems graphically.
Steps to Apply Algebraic Methods Effectively
- Identify the Problem Type: Recognize whether you need to solve an equation, factor an expression, or apply another method.
- Choose the Best Method: Select the most efficient technique for the problem at hand based on the given information.
- Perform Calculations Step by Step: Carefully execute each step, making sure not to skip any part of the process.
- Double-Check Your Work: Verify your results by substituting your solution back into the original equation or problem to ensure it makes sense.
By mastering these algebraic techniques and applying them systematically, you can tackle a wide range of problems with greater confidence and ease.
Breaking Down Complex Algebraic Expressions
When faced with complicated mathematical expressions, breaking them down into simpler components can make the solution process more manageable. By systematically applying certain techniques, you can simplify and manipulate complex terms to reveal the underlying relationships. This approach allows for easier calculation and a clearer understanding of the problem.
Techniques for Simplifying Expressions
- Factorization: Split the expression into its factors. This allows you to identify common terms and simplify the problem.
- Combining Like Terms: Group similar terms together to reduce the complexity. Terms with the same variable and exponent can be added or subtracted.
- Distributive Property: Use this property to eliminate parentheses by distributing a term across terms inside parentheses, simplifying the expression further.
- Grouping: Group terms based on their common factors or exponents to make the expression easier to handle.
- Substitution: Replace variables with known values to reduce the complexity of the expression and make calculations easier.
Step-by-Step Process for Simplification
- Identify Common Terms: Look for terms that share the same variable or constant, as these can often be combined or factored.
- Apply the Distributive Property: Use distribution to simplify expressions involving parentheses.
- Combine Like Terms: Add or subtract terms with the same variable or constant to simplify the expression.
- Factor and Group: Factor out common elements and group terms in a way that makes further simplification easier.
- Substitute Known Values: If applicable, substitute known values to make the expression simpler to evaluate.
By breaking down complex expressions in this manner, you can gain a clearer insight into the problem and efficiently reach a solution.
Understanding Word Problems in Algebra
Word problems can often seem intimidating because they require translating real-world scenarios into mathematical expressions. However, with a clear approach, you can break down the information and solve these problems efficiently. The key is to carefully read through the text, identify the important data, and then form equations that represent the situation.
To solve word problems, it’s essential to first understand the context and determine what the problem is asking. Once the variables are identified, you can use mathematical operations to relate the known and unknown values. By organizing the information logically, you will be able to simplify the problem and reach a solution.
Approaching word problems step by step, without rushing, helps avoid confusion and ensures that you don’t overlook critical details. With practice, solving these types of problems becomes more intuitive and manageable.
Key Formulas for Section 7
In this part of the curriculum, understanding key formulas is crucial for solving a variety of mathematical problems. These formulas serve as foundational tools that help simplify complex expressions and guide you through solving equations or identifying patterns. Mastering them allows you to approach problems with greater confidence and precision.
Each formula represents a specific mathematical principle, and knowing when and how to apply them is essential for effective problem-solving. Whether you’re working with linear equations, quadratic expressions, or other mathematical operations, these formulas provide a structured method for reaching accurate solutions.
Practice Problems for Mastery
To truly master any mathematical skill, consistent practice is essential. By solving a variety of problems, you not only reinforce your understanding but also develop the ability to apply concepts in different contexts. Practicing regularly helps you identify patterns, sharpen problem-solving techniques, and gain confidence in your skills.
These practice problems are designed to challenge your current knowledge while helping you improve step by step. They cover different levels of difficulty, allowing you to gradually build up your expertise. The more problems you solve, the better prepared you’ll be for more complex challenges ahead.
Start with simple exercises to warm up your skills, and then move on to more advanced problems. Don’t rush the process–focus on understanding each step thoroughly before moving on to the next.
How to Improve Skills Quickly

Improving mathematical skills in a short period requires focused practice, the right resources, and an understanding of core concepts. The key to rapid progress is to identify areas where you struggle the most and dedicate extra time to mastering them. Consistent effort combined with smart strategies leads to quick improvements.
One effective way to speed up the learning process is by breaking down complex problems into simpler parts and solving them step by step. Additionally, revisiting foundational concepts and practicing regularly will help reinforce understanding and improve problem-solving efficiency.
| Strategy | Action |
|---|---|
| Focus on Weak Areas | Identify and concentrate on the areas where you struggle the most. Use additional practice materials and explanations to strengthen those concepts. |
| Practice Regularly | Set aside time each day to solve problems. The more you practice, the more familiar you become with different types of questions and solutions. |
| Learn from Mistakes | When you make an error, analyze it carefully to understand what went wrong. This helps prevent the same mistakes from happening again. |
| Use Online Resources | Take advantage of online tutorials, forums, and practice problems. These can offer additional explanations and examples that may make concepts clearer. |
By applying these strategies consistently, you’ll improve your mathematical skills more quickly and with greater confidence.
Section 7: What to Expect
In this part of the course, you will encounter a variety of problems designed to test your understanding of key mathematical principles. These exercises will cover a range of concepts, helping you to strengthen your problem-solving skills and apply your knowledge in new ways. The goal is to challenge your abilities and prepare you for more advanced material in future sections.
The topics in this section may seem complex at first, but with careful attention to detail and a systematic approach, they become manageable. You’ll be expected to work with equations, analyze relationships between variables, and apply learned techniques to solve practical problems. Expect to see both theoretical questions as well as real-world scenarios that require logical reasoning.
Key Concepts to Focus On

Pay close attention to the methods that help you break down complex problems into simpler steps. Mastery of these techniques is essential for tackling the more difficult exercises in this section.
Approach to Problem Solving
Start with the basics, build a strong foundation, and progressively tackle harder problems. This section is an excellent opportunity to solidify your mathematical thinking and improve your overall skills.
Why This Tool is a Useful Resource
This platform serves as a valuable resource for learners looking to improve their mathematical skills. Offering a wide range of features, it provides both structured lessons and interactive tools that cater to different learning styles. Whether you’re a visual learner or someone who thrives with hands-on practice, this tool has the necessary resources to help you succeed.
One of the main benefits of this platform is its accessibility. Users can learn at their own pace, revisit difficult concepts, and practice through engaging exercises. The platform’s interactive nature makes it easier to track progress and identify areas that need improvement, making the learning process more efficient and tailored to individual needs.
| Feature | Benefit |
|---|---|
| Interactive Lessons | Engage with material in a hands-on way, making complex concepts easier to understand and apply. |
| Progress Tracking | Monitor your improvements over time and focus on areas where you need additional practice. |
| Practice Problems | Test your understanding and reinforce learning through a wide variety of problem types. |
| Accessibility | Learn at your own pace, anytime and anywhere, making it easy to fit study into your schedule. |
With its comprehensive approach, this tool ensures that learners can build a strong foundation in mathematics, providing the resources and support needed to succeed in both basic and advanced topics.
Essential Strategies for Success
To excel in mathematical problem-solving, adopting the right approach is crucial. Success comes not only from understanding theory but also from practicing consistently and applying learned techniques in various situations. This section outlines essential strategies that will help you tackle challenges effectively and improve your skills over time.
One of the most important strategies is breaking down complex problems into smaller, manageable parts. This method allows you to understand the underlying structure and identify the best approach to solving them. Additionally, practicing regularly with different problem types builds confidence and reinforces learning.
Another key strategy is reviewing past mistakes. Understanding where you went wrong is an invaluable learning tool. By analyzing errors, you can avoid repeating them and strengthen your problem-solving skills. Consistent reflection and adjustment lead to more effective learning outcomes.
Lastly, don’t hesitate to seek support when needed. Whether through online resources, study groups, or tutors, asking for help can provide new insights and speed up your learning process. Collaboration often leads to a deeper understanding of concepts, and sharing knowledge strengthens both comprehension and application.
Reviewing Key Solutions for Mastery
Understanding and reviewing problem solutions is an essential step towards mastering mathematical concepts. By thoroughly going over solutions, you not only reinforce your knowledge but also gain insights into efficient problem-solving techniques. This process allows you to identify patterns, common approaches, and key principles that can be applied to future challenges.
Steps to Effectively Review Solutions
- Identify Core Concepts: Focus on the key ideas behind each problem. Understand why certain steps are taken and how they contribute to solving the equation.
- Revisit Mistakes: Pay close attention to any errors made during the process. Analyzing where things went wrong helps you avoid repeating the same mistakes in the future.
- Practice Similar Problems: After reviewing, work on similar exercises to solidify your understanding. This will help you internalize the methods and become more comfortable with various types of problems.
Why Reviewing is Crucial
- Strengthens Problem-Solving Skills: The more you review, the better you become at recognizing strategies and applying them to new problems.
- Builds Confidence: With practice and understanding of the solutions, your confidence in tackling more complex problems increases.
- Enhances Retention: Regularly reviewing solutions helps reinforce memory and ensures that the knowledge stays with you over time.
Preparing for Tests with Key Solutions
Effective test preparation requires more than just reviewing notes; it involves understanding the underlying principles that govern problem-solving. By analyzing and reflecting on previous solutions, you can build a solid foundation for tackling similar problems during exams. This approach not only improves your problem-solving speed but also helps you internalize the steps necessary to achieve accurate results under pressure.
Step-by-Step Practice: Focus on practicing problems that resemble those you may encounter in the exam. By working through examples with solutions, you gain a deeper understanding of the process and enhance your ability to apply techniques correctly when faced with time constraints.
Identifying Common Pitfalls: One key advantage of reviewing solutions is the opportunity to identify and avoid common mistakes. Recognizing where errors typically occur helps you remain cautious and accurate during the test. Make note of frequent errors and work on strategies to overcome them before the exam day.
Timed Simulations: Simulate test conditions by timing yourself while solving practice problems. This exercise helps you manage your time effectively during the actual exam and teaches you how to stay calm under pressure.