Algebra 2 Final Exam Multiple Choice Answers

In order to succeed in advanced mathematics assessments, it’s crucial to have a solid grasp of the material being tested. Many students find themselves facing questions that challenge their understanding of important concepts, requiring not just rote memorization but also the ability to apply learned skills effectively. Preparing well for such challenges can make all the difference in achieving a high score.

One of the most effective ways to approach these assessments is by focusing on problem-solving techniques and understanding the core principles behind each topic. This approach helps you navigate through questions with confidence, even when they seem difficult at first glance. Being familiar with the structure and common patterns of questions allows you to quickly identify the correct solutions, giving you a competitive edge.

Strategic practice is key to mastering the necessary skills. With the right preparation, you can approach each problem methodically, using logic and reasoning to eliminate incorrect options. By reinforcing your understanding and practicing consistently, you set yourself up for success in any test format.

Algebra 2 Final Assessment Response Guide

Success in any comprehensive mathematics assessment relies on more than just recalling formulas; it requires a deep understanding of underlying principles and the ability to apply them accurately under timed conditions. For many students, the ability to decipher questions and quickly select the correct solution can be the difference between a good and excellent result. Focusing on key problem-solving strategies ensures you can confidently navigate through various question types, regardless of difficulty.

Understanding the Problem Structure

In assessments that test higher-level math, questions are often structured to challenge your reasoning skills. While some may appear complex at first, with the right approach, they can be broken down into simpler components. Recognizing familiar patterns and understanding the relationships between variables and equations will allow you to more easily pinpoint the correct solution from available options.

Techniques for Maximizing Your Score

One of the most important strategies is to practice applying theoretical knowledge in different problem scenarios. By engaging with sample problems and mock tests, you can enhance your critical thinking abilities and learn to quickly recognize the most efficient solving methods. Additionally, developing the skill to eliminate obviously incorrect options helps improve your chances of selecting the right response even when time is tight.

Overview of Algebra 2 Assessment Format

Understanding the layout and structure of a mathematics assessment is crucial for performing well. Each test is designed to evaluate a student’s mastery over a wide range of topics and problem-solving techniques. The format typically combines various question types that assess both theoretical knowledge and practical application of mathematical concepts. Knowing how the test is organized can help you manage your time and approach each problem strategically.

The majority of questions are designed to test your ability to apply key formulas, solve equations, and analyze functions. These problems may appear in different forms, ranging from straightforward calculations to more complex, multi-step problems that require critical thinking. In addition to the core content, some questions may involve word problems, which assess your ability to interpret real-world scenarios mathematically.

Time management is essential during these assessments. With limited time to answer each question, it’s important to quickly evaluate the options available and move through the problems efficiently. Practicing with sample tests and familiarizing yourself with the question styles can significantly improve your speed and accuracy under pressure.

Key Topics Covered in Algebra 2

A comprehensive understanding of key mathematical principles is essential for success in advanced problem-solving assessments. The subject at hand covers a wide range of topics that require both theoretical knowledge and the ability to apply concepts to different problem types. Familiarity with these topics will help you navigate through complex questions with greater confidence and efficiency.

• Quadratic Equations: Solving, graphing, and interpreting equations involving squared terms.
• Polynomials: Operations with polynomial expressions, factoring, and solving polynomial equations.
• Exponential Functions: Understanding growth and decay models, solving equations with exponents.
• Rational Expressions: Simplifying and solving problems involving fractions with polynomials in the numerator or denominator.
• Radical Expressions: Working with square roots and higher roots, simplifying and solving radical equations.
• Systems of Equations: Solving systems using substitution, elimination, and matrix methods.
• Logarithmic Functions: Converting between exponential and logarithmic forms, solving logarithmic equations.
• Sequences and Series: Understanding arithmetic and geometric sequences, and summing series.

Each of these areas requires careful study and practice. Mastery of these topics not only helps with immediate problem-solving tasks but also builds the foundation for more advanced mathematics. By focusing on these key subjects, you’ll be well-prepared to handle any challenge that comes your way in an assessment.

Understanding Multiple Choice Questions

To excel in assessments that require quick decision-making, it’s important to understand how questions are structured and what is expected in each scenario. These types of problems often present a set of options, with only one correct solution. Understanding how to analyze and interpret these options will give you the best chance of selecting the correct response and maximizing your score.

The key to answering such questions correctly lies in breaking down each option systematically. By recognizing common patterns and applying your knowledge of the subject, you can narrow down the possibilities and eliminate incorrect choices. This approach minimizes the risk of mistakes and improves your chances of identifying the right answer.

Step	Description
Step 1	Read the question carefully, noting any keywords or phrases that point to the correct concept.
Step 2	Evaluate all options. Sometimes, one option will be clearly incorrect or out of context.
Step 3	Use your knowledge to test the remaining choices. If possible, eliminate the most obviously wrong options.
Step 4	Make your selection and move on, ensuring you don’t second-guess yourself unnecessarily.

By following these steps, you can approach each question with greater confidence, allowing you to answer efficiently and correctly under time pressure.

Common Algebra 2 Question Types

Assessments in advanced mathematics often feature a variety of question types, each designed to test a specific skill or concept. Familiarizing yourself with the common formats will allow you to approach each question with a clear strategy, improving both your speed and accuracy. Below are some of the typical question types you may encounter.

• Equation Solving: These questions test your ability to solve linear, quadratic, or higher-degree equations by using various methods, such as factoring or the quadratic formula.
• Graph Interpretation: Questions in this category ask you to analyze graphs and extract key information, such as slopes, intercepts, and points of intersection.
• Function Evaluation: These questions require you to substitute values into given functions and simplify the expressions to find the output.
• Word Problems: Word-based problems assess your ability to translate real-world situations into mathematical equations and solve them accordingly.
• Expression Simplification: Questions focusing on simplifying algebraic expressions by factoring, expanding, or reducing terms.
• Systems of Equations: These questions involve solving two or more equations simultaneously using methods like substitution, elimination, or matrix operations.
• Inequalities: These problems test your knowledge of solving and graphing inequalities, including both linear and quadratic forms.
• Exponential and Logarithmic Problems: Questions related to exponential growth, decay, and their logarithmic counterparts.

By understanding the different types of problems and practicing each one, you will be better prepared to navigate a range of question formats efficiently and confidently.

Strategies for Answering Algebra 2 Questions

Approaching mathematics problems with a clear strategy can significantly enhance your performance. By following effective problem-solving techniques, you can tackle even the most complex questions with greater confidence. Developing a systematic approach will help you work efficiently under time pressure and reduce the chances of making careless mistakes.

One important strategy is to break down each question into smaller, more manageable parts. This allows you to focus on one aspect of the problem at a time, making it easier to find the correct solution. Additionally, always double-check your work before moving on to the next problem, especially when dealing with lengthy calculations or multiple steps.

Another useful approach is to eliminate incorrect options when faced with questions that provide several choices. By quickly discarding answers that are obviously wrong, you can increase your chances of selecting the correct one. In cases where you’re uncertain, rely on your knowledge of key concepts and use logical reasoning to guide your decision-making.

Finally, practicing consistently with different types of questions will help you become familiar with common patterns and problem structures. With enough practice, you’ll be able to identify the most effective solving methods, making the test-taking process smoother and more efficient.

How to Prepare for the Assessment

Proper preparation is the key to performing well on any comprehensive test. The more thoroughly you prepare, the more confident you will feel when facing a variety of problem types. A well-structured study plan, along with targeted practice, will help ensure that you are ready for the challenges ahead.

Review Core Concepts and Techniques

Start by revisiting the fundamental concepts that are most likely to appear in the test. Ensure that you understand key topics such as solving equations, interpreting graphs, and simplifying expressions. Focus on the methods and strategies that you have learned throughout the course, as these will form the basis for solving problems in the assessment.

Practice with Sample Problems

Once you have a solid grasp of the material, begin working through practice problems. The more you practice, the more familiar you will become with the types of questions you might encounter. Focus on timing yourself during these practice sessions to simulate the conditions of the actual assessment. This will help you get accustomed to managing your time and answering questions efficiently.

Practice Problems for Algebra 2 Review

Practicing with a variety of problems is one of the most effective ways to reinforce your understanding and sharpen your problem-solving skills. By working through different types of questions, you can identify areas where you need more review and build confidence in tackling complex scenarios. Below are a few sample problems to help you prepare for the assessment.

• Solve for x: 3x + 5 = 20
• Factor the expression: x² + 7x + 12
• Graph the function: y = 2x – 4
• Evaluate the function: f(x) = 3x² – 2x + 1, when x = 4
• Find the solution to the system:
  • 2x + 3y = 10
  • 4x – y = 3
• Simplify the expression: (4x² – 3x + 7) – (2x² + x – 5)
• Solve the inequality: 5x – 3 ≥ 2x + 4

By completing these problems and reviewing the solutions, you’ll become more comfortable with the techniques needed to solve similar questions in the assessment. Be sure to pay attention to any mistakes you make and focus on understanding why the correct approach works. Regular practice will help you build the skills necessary for success.

Common Mistakes to Avoid on the Test

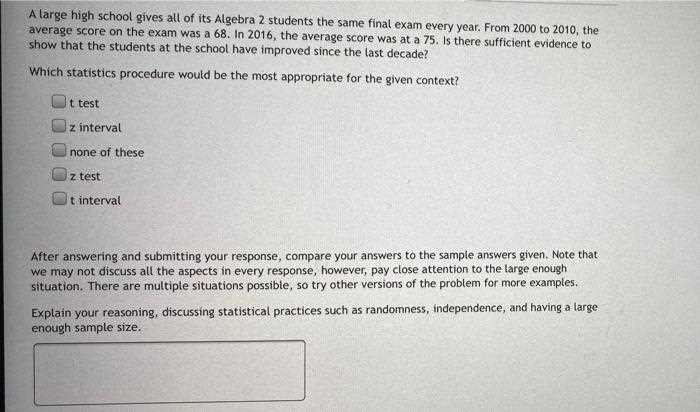
While preparing for any assessment, it’s crucial to not only focus on strengthening your knowledge but also to be aware of common pitfalls that can lead to mistakes. By identifying these common errors in advance, you can take steps to avoid them during the actual test, ultimately improving your performance.

Rushing Through the Questions

One of the most frequent mistakes students make is rushing through questions, especially under time pressure. While it’s important to manage time, hastily answering can lead to simple calculation errors or overlooking key details in the problem. Take the time to read each question carefully, ensuring you fully understand what is being asked before selecting your answer.

Misinterpreting the Problem

Another common mistake is misinterpreting the problem. This often happens when students fail to properly identify what the question is asking for, especially in word-based problems. Make sure to underline key terms, identify what the question is asking for, and check whether the problem requires a value, an equation, or an expression.

Tip: Always re-read the problem if you’re unsure about the requirements. This simple habit can help clarify your approach and reduce errors.

Overlooking Negative Signs: Pay close attention to negative signs, both in equations and during simplification steps. It’s easy to miss or misapply a negative, which can lead to incorrect solutions. Double-check all your steps to ensure signs are handled correctly.

Final Thought: Avoiding these common mistakes requires practice and mindfulness. The more you prepare with these potential errors in mind, the less likely they will affect your performance during the assessment.

Effective Time Management During the Test

Proper time management is essential for performing well during any assessment. Without an effective strategy, it’s easy to get caught up in difficult questions and lose valuable time, which can affect your overall performance. By managing your time wisely, you can ensure that you have enough opportunity to address every question and make thoughtful decisions.

Plan Your Time Wisely

Before you begin, quickly glance over the entire test to gauge its difficulty and how much time you can realistically allocate to each section. Divide your time based on the number of questions and their complexity. It may be helpful to spend more time on questions that require detailed problem-solving, while reserving a quicker pace for simpler ones.

Don’t Get Stuck on One Question

If you encounter a question that seems particularly challenging, don’t spend too much time on it. It’s easy to become fixated on a difficult problem, but this can prevent you from completing the rest of the test. Mark the question and return to it later if time allows. Prioritize questions that are easier to answer first to build momentum and boost your confidence.

By following a time management strategy, you can maximize your chances of success. Staying calm, moving at a steady pace, and recognizing when to move on will help you maintain focus throughout the test.

Tips for Eliminating Incorrect Choices

When faced with a set of options, one effective strategy for improving your chances of selecting the correct response is to narrow down your choices by eliminating the incorrect ones. This approach helps you focus on the most likely solutions, saving valuable time and increasing your accuracy during the assessment.

Look for Extreme or Unlikely Options

Oftentimes, options that seem unusually high, low, or extreme can be easily ruled out. If a choice doesn’t logically fit with the problem or the context, it’s likely incorrect. Look for these outliers and eliminate them first, narrowing down your remaining options.

Check for Common Traps and Misleading Clues

Test creators often include answers that are designed to trick you. These can include options that are similar to common mistakes made in calculations, such as reversing signs or misapplying formulas. Be vigilant about these patterns and eliminate them by double-checking your work.

Tip: If you can’t immediately identify the correct answer, use the process of elimination to progressively rule out the least likely choices. This increases the odds of selecting the correct option when you must make an educated guess.

Final Thought: By carefully analyzing each option and eliminating the ones that are obviously incorrect, you significantly increase your chances of finding the right response and improving your performance in the assessment.

Breaking Down Complex Problems

When faced with a challenging problem, it’s essential to break it down into smaller, more manageable steps. This method allows you to analyze each part individually and tackle the task with a clearer, more structured approach. By simplifying the problem, you can avoid feeling overwhelmed and work through it step by step.

Start by identifying the key elements of the problem. Look for the known values, the relationships between variables, and any instructions that indicate the required steps. Once you have a clear understanding of the problem, proceed to isolate each part and solve it separately.

For example, if you are working with an equation that involves multiple operations, begin by addressing the most straightforward components first, such as simplifying expressions or factoring terms. Then, work through any more complex processes, such as solving for unknown variables or applying specific rules to manipulate the equation.

By organizing your approach in this way, you can reduce the complexity of the problem and make the solution process more efficient and less intimidating. Every small success along the way will help you move closer to the correct outcome with confidence and clarity.

How to Solve Word Problems Efficiently

Word problems can often feel overwhelming, especially when they contain a lot of information. However, with a systematic approach, you can break down the problem into manageable parts and solve it efficiently. The key is to identify the important details and translate them into mathematical expressions or equations step by step.

Step 1: Read and Understand the Problem

Before jumping into calculations, carefully read the problem. Pay attention to the following:

• The specific question being asked
• The given information, such as numbers or variables
• Any relationships or conditions between the quantities

Take notes or underline important parts of the problem. This helps clarify what you are trying to find and ensures that you don’t miss any key details.

Step 2: Translate Words into Equations

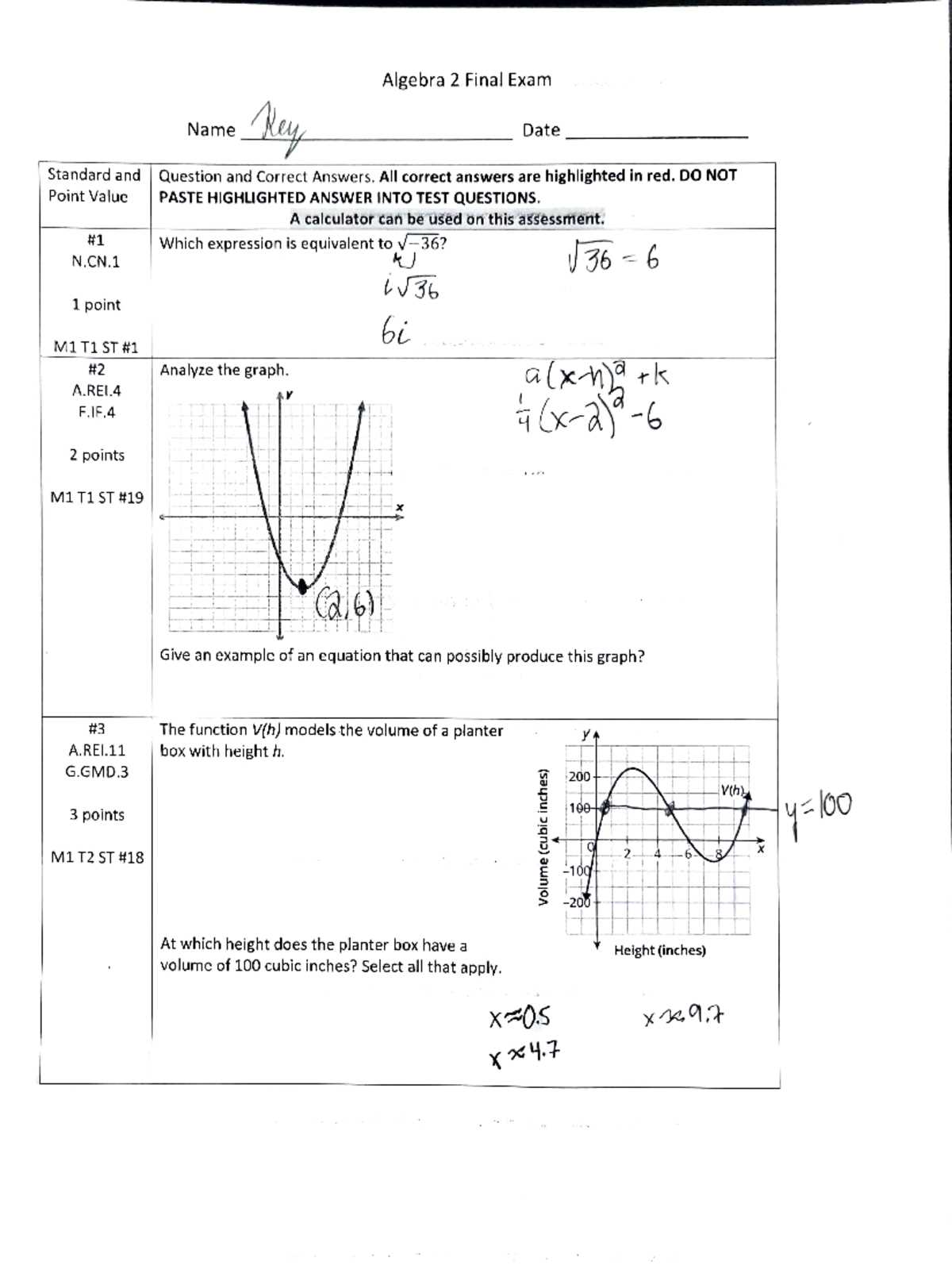
Once you’ve understood the problem, convert the information into a mathematical format. This could mean setting up an equation, identifying variables, or translating word phrases into mathematical operations. For example:

• “The sum of a number and 5” becomes “x + 5”.
• “Twice a number” becomes “2x”.
• “The difference between two numbers” becomes “x – y”.

After setting up the equation, proceed with solving it as you would with any standard problem, ensuring each step follows logically from the previous one.

Step 3: Solve and Check Your Work

Once you’ve created the equation, solve for the unknown value. Afterward, it’s crucial to check your work to ensure the solution makes sense in the context of the problem. Substitute the value back into the original situation to see if it satisfies the conditions given. If the result seems off, recheck your steps for any mistakes.

By following these steps, you can simplify the process of solving word problems and approach each one with confidence.

Utilizing Formulas and Theorems

Mastering various formulas and theorems is essential for efficiently solving problems in mathematical fields. These tools provide a framework for addressing complex tasks, turning them into straightforward calculations. Understanding how and when to apply specific formulas can significantly streamline your problem-solving process and increase accuracy.

Understanding Key Formulas

Before diving into problems, it’s important to familiarize yourself with the most commonly used formulas in your studies. These formulas serve as shortcuts that allow you to solve problems without having to work through lengthy steps. Here are some common types to remember:

• Quadratic formula: Used to solve quadratic equations.
• Area and Volume formulas: Crucial for geometry-related problems.
• Exponential and logarithmic equations: For solving growth and decay problems.

Applying Theorems to Simplify Solutions

Theorems provide foundational rules that apply to specific scenarios, simplifying problem-solving. Familiarity with key theorems helps you recognize when to apply them, saving time and reducing the chance of errors. Some widely used theorems include:

• Pythagorean Theorem: Used for right-angled triangle problems.
• Binomial Theorem: Helpful in expanding binomials.
• Fundamental Theorem of Arithmetic: Assists in factoring and simplifying expressions.

By recognizing patterns and knowing which formulas and theorems to apply, you can solve problems more efficiently and with greater confidence. Practice using these tools regularly to ensure you’re well-prepared for more challenging tasks.

Resources for Studying Algebra 2

Having the right resources can make a significant difference in mastering mathematical concepts. From textbooks to online platforms, various tools are available to help students prepare effectively and reinforce their understanding of key topics. Utilizing diverse study materials ensures a well-rounded grasp of essential skills and concepts.

Books and Textbooks

Textbooks are a traditional but valuable resource. They provide structured lessons and examples, guiding students through concepts with step-by-step instructions. Some highly recommended textbooks include:

Resource	Description
Prentice Hall Mathematics	A comprehensive guide that covers fundamental concepts and practice problems.
McGraw-Hill Education	Offers practice exercises and real-world examples to apply concepts.
CK-12	Free, online textbook that provides interactive lessons and practice questions.

Online Platforms and Websites

In addition to textbooks, online platforms can provide interactive lessons, tutorials, and practice problems. Some popular online resources include:

• Khan Academy: Offers video tutorials and practice exercises on a wide range of topics.
• Wolfram Alpha: Useful for solving equations and visualizing graphs.
• IXL Learning: Provides personalized practice problems based on your current level.

By combining different resources, you can better understand challenging concepts and feel more confident in applying them. Make sure to choose materials that align with your learning style to enhance your overall study experience.

What to Do After the Exam

Once you’ve completed a major assessment, it’s important to take steps to ensure a positive outcome and continue progressing in your academic journey. The period following an assessment can be just as crucial as the preparation itself. Reflecting on your performance and taking action based on what you’ve learned can help you build confidence and stay on track for future challenges.

Here are some key things to consider once the test is over:

• Review Your Performance: If possible, go over the problems you found most challenging. Understanding where you made mistakes can help you avoid similar errors in the future and strengthen your problem-solving skills.
• Seek Feedback: Don’t hesitate to ask your teacher for feedback on your work. This can provide valuable insights into areas where you need improvement.
• Take Care of Yourself: After an intense study and testing period, it’s important to relax and recharge. Take some time to unwind, ensuring you’re mentally refreshed for upcoming challenges.
• Prepare for the Next Step: Use the time after the assessment to start preparing for the next set of topics. Revisiting material shortly after the test can reinforce your understanding and keep the information fresh.

By reflecting on your performance and focusing on continuous improvement, you can enhance your learning process and approach future assessments with greater confidence.

How to Handle Test Anxiety

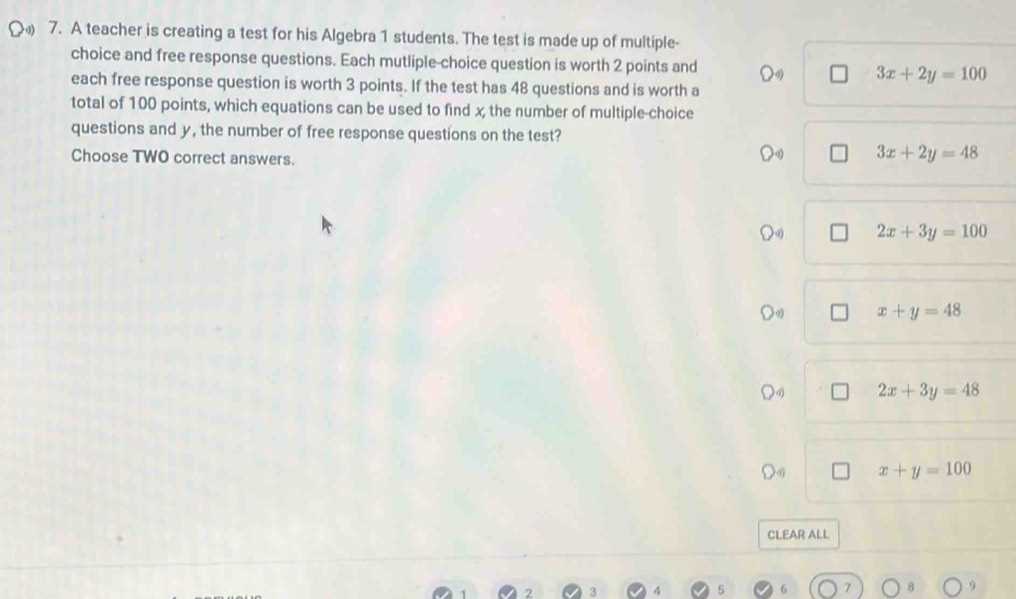
Test-related stress is a common experience, and learning how to manage it effectively can greatly improve your performance and overall well-being. Anxiety can cloud your thinking, make it harder to focus, and even undermine your preparation. By employing various techniques to stay calm and focused, you can transform anxiety into a tool for success rather than a hindrance.

Here are some practical strategies to manage stress during assessments:

Strategy	How It Helps
Practice Deep Breathing	Taking slow, deep breaths helps to calm the nervous system, reducing anxiety and improving focus.
Stay Positive	Focus on positive thoughts, reminding yourself that you are prepared and capable of handling the task at hand.
Break the Test into Sections	Divide the test into smaller, more manageable parts to prevent feeling overwhelmed. Tackle one section at a time.
Visualize Success	Take a few moments to visualize yourself answering the questions with ease. Positive visualization can reduce anxiety and boost confidence.
Get Enough Rest	A good night’s sleep before the test helps your brain function at its best and reduces stress.

By adopting these techniques and maintaining a calm mindset, you can improve both your test-taking experience and your ability to perform at your best, no matter the circumstances.

Improving Your Algebra 2 Skills Post-Exam

After completing an assessment, it’s important to continue refining your skills. Reflecting on your performance and identifying areas for improvement can help you strengthen your understanding and prepare for future challenges. Post-assessment review is an excellent opportunity to deepen your knowledge, correct misunderstandings, and build confidence in your abilities.

Here are some effective strategies to improve your skills after taking the test:

• Review Mistakes: Carefully analyze any questions you found challenging. Identify the areas where you made errors and take time to understand why your approach didn’t work. This will help you avoid similar mistakes in the future.
• Practice Regularly: Consistent practice is essential for mastering complex concepts. Set aside time each week to work on new problems or revisit difficult topics to reinforce your learning.
• Seek Help if Needed: If you’re struggling with certain topics, don’t hesitate to reach out for additional support. Tutors, classmates, or online resources can provide explanations and different perspectives that can help clarify difficult concepts.
• Apply Real-Life Examples: Try to connect abstract concepts with real-life scenarios. This can help make the material more relatable and easier to understand, solidifying your grasp on the subject.
• Focus on Understanding, Not Memorization: Instead of relying solely on memorizing formulas or procedures, focus on understanding the underlying principles behind them. This deeper understanding will allow you to approach problems more effectively and flexibly.

By incorporating these strategies into your routine, you can continuously improve your problem-solving abilities and gain greater confidence in your skills, ensuring success in future challenges.