CPM Answer Key Course 3 Solutions and Guide

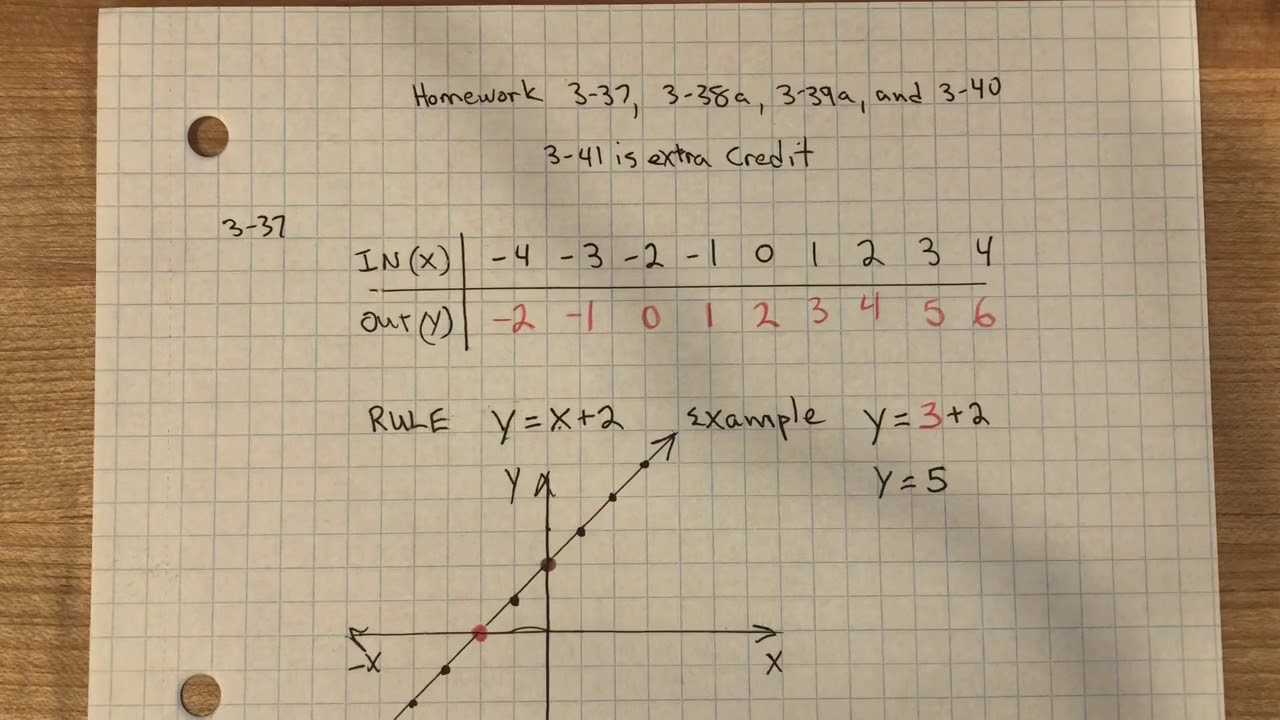
When tackling complex mathematical exercises, having the right resources at hand can make all the difference in achieving success. A structured set of solutions can guide students through each problem, offering step-by-step explanations that enhance understanding and help improve problem-solving skills.

In this section, you will find a comprehensive collection of methods and answers that clarify common challenges in advanced math topics. By following these detailed solutions, learners can gain a deeper insight into mathematical concepts and refine their approach to solving difficult tasks.

Whether you are looking to verify your work or seeking additional support in understanding specific techniques, this guide will provide the necessary tools for mastering various mathematical skills. Practice and careful analysis of the solutions can lead to better outcomes and greater confidence in applying these principles in future problems.

CPM Answer Key Course 3 Overview

In mathematics, understanding the problem-solving process is just as important as finding the correct solution. This section provides a thorough breakdown of how to approach and resolve complex problems typically encountered in advanced levels of study. By offering clear explanations and organized methods, learners can gain a deeper understanding of mathematical concepts and improve their problem-solving strategies.

The resources provided offer a structured format that makes it easier to follow along, ensuring that every step is clearly explained. The goal is to help students not only arrive at the correct answers but also understand the reasoning behind each solution. This approach encourages critical thinking and strengthens skills needed for tackling future problems.

Problem Type	Solution Approach	Key Concepts Covered
Linear Equations	Simplifying equations, isolating variables	Algebra, equation solving
Graphing	Plotting points, analyzing slopes	Coordinate geometry, functions
Word Problems	Translating words into equations	Problem-solving, real-world applications
Polynomials	Factoring, expanding	Algebraic expressions, factorization

Each problem type is addressed with a focus on both methodology and application. This ensures that students are well-equipped to handle similar challenges in future learning environments. By mastering the techniques outlined, learners will gain a solid foundation in mathematical reasoning and be prepared for more advanced topics in their academic journey.

How to Use CPM Answer Keys Effectively

Using resources that provide solutions to math problems can greatly enhance a student’s learning process. However, it’s important to approach these materials with a clear strategy in order to fully benefit from them. Simply looking at the final answers without understanding the steps involved can limit the value of these resources. A more effective way is to use the solutions as a tool for reinforcing understanding and improving problem-solving techniques.

Focus on the Process

Instead of only checking the answers, take the time to study the steps taken to reach the solution. Pay attention to the methods, rules, and reasoning behind each step. This will allow you to replicate the process on similar problems and deepen your grasp of the underlying mathematical concepts.

Identify Areas of Improvement

As you review the provided solutions, identify where you struggled or made mistakes. Use the corrected approach as a guide to help you understand where you went wrong. Focus on those areas to strengthen your skills and avoid repeating the same errors in the future.

By integrating these solutions into your practice sessions and approaching them with a mindset of learning, you will significantly improve both your problem-solving abilities and overall understanding of the subject matter.

Understanding CPM Course 3 Concepts

Mastering complex mathematical concepts requires a clear understanding of the core principles and their applications. This section delves into the key topics and strategies used to solve advanced problems, focusing on developing a deeper comprehension of each concept. Gaining insight into these ideas not only helps solve problems more effectively but also prepares students for higher-level studies.

Key Mathematical Areas in Advanced Studies

Advanced mathematics covers a range of areas that require both conceptual understanding and practical application. Students are expected to be familiar with algebraic methods, geometric principles, and problem-solving techniques. It’s important to approach these areas systematically to build a strong foundation for future learning.

Topic	Core Concept	Application
Linear Functions	Understanding slope and intercept	Graphing equations, real-world problem-solving
Quadratic Equations	Factoring and solving roots	Solving for unknowns, applications in physics
Systems of Equations	Solving multiple equations simultaneously	Analyzing multiple variables, optimization problems
Exponents and Polynomials	Manipulating powers and coefficients	Simplifying expressions, algebraic expansions

Approaching Problems with a Strategic Mindset

Understanding the fundamental principles is crucial for approaching complex problems strategically. By breaking down each problem into manageable parts, students can apply the appropriate methods and techniques for efficient solutions. This strategic mindset ensures that students develop a deep understanding, rather than relying solely on memorization.

Common Challenges in Course 3 Problems

Mathematical problems in advanced levels often present unique challenges that can be difficult to navigate. Understanding these obstacles is the first step toward overcoming them. By identifying common struggles, students can better prepare themselves and apply the right strategies to solve problems with confidence.

Identifying and Solving Complex Word Problems

One of the most frequent challenges students face is interpreting word problems. These types of exercises require translating real-world scenarios into mathematical expressions. The key to overcoming this challenge is breaking down the information systematically and focusing on the relevant details. Once the problem is properly framed, the solution becomes much more manageable.

Mastering Abstract Algebraic Concepts

Another area that many learners struggle with is abstract algebra. Concepts such as factoring polynomials, manipulating exponents, and solving systems of equations can seem overwhelming. To navigate this, it’s important to build a strong understanding of the basic principles and practice regularly. Mastering the foundational techniques will make these more advanced topics easier to approach.

Step-by-Step Guide to CPM Solutions

Solving complex mathematical problems requires a systematic approach that breaks down each task into manageable steps. This section outlines a clear, structured method for approaching problems, ensuring that students can follow each phase of the solution process. By following these steps, learners can build confidence and sharpen their problem-solving skills.

Step 1: Understand the Problem

The first step is to thoroughly read and comprehend the problem. Identify key information such as variables, constants, and relationships between different elements. Make sure to highlight or note down any important values or conditions that will guide the solution process. Understanding what is being asked is crucial before proceeding to the next step.

Step 2: Develop a Strategy

Once the problem is understood, devise a plan to solve it. Choose the appropriate mathematical operations or methods needed to solve for the unknowns. This could include using algebraic formulas, graphing, or applying specific rules and theorems. Break the process down into smaller tasks and tackle them one by one to keep the solution organized and manageable.

By following these steps, students can approach each problem methodically, increasing the likelihood of a correct solution while gaining valuable experience in the problem-solving process.

Improving Math Skills with CPM Answers

Strengthening mathematical abilities requires consistent practice and a deep understanding of core concepts. Resources that provide solutions to problems not only offer the correct results but also demonstrate the methods and strategies used to reach them. By analyzing these solutions, students can improve their problem-solving techniques and build a stronger foundation for more advanced topics.

One of the most effective ways to enhance math skills is by reviewing and studying the steps behind each solution. Understanding the process behind the answer allows students to apply the same techniques to similar problems, reinforcing key concepts and making them more intuitive. The ability to recognize which method to apply in different situations is a crucial skill that will improve over time with practice.

Active learning plays a significant role in this process. Rather than passively reading the solutions, students should attempt to solve the problems themselves first. Afterward, they can compare their methods with the provided solutions to identify any gaps in understanding. This reflection process leads to more effective learning and faster mastery of challenging topics.

What You Need to Know About CPM Course 3

To excel in advanced math problems, it’s crucial to understand the structure and methods presented in your learning materials. This section explores the essential elements of the third level of the program, highlighting the key topics and strategies you’ll encounter. By grasping these core ideas, students can build a strong foundation and approach problems with greater confidence and clarity.

Core Concepts and Topics

The third level focuses on more advanced mathematical principles, expanding upon the basics learned in previous stages. Key topics include:

• Linear and quadratic functions
• Systems of equations and inequalities
• Polynomials and factoring techniques
• Geometric transformations and their applications

Each of these areas requires a different set of problem-solving skills, and understanding their interconnections is essential for mastering the material. Consistent practice and application of these concepts will help solidify your knowledge and improve your ability to tackle more complex problems.

Approach to Problem Solving

The method for solving problems in this level emphasizes logical reasoning and strategic thinking. Students are encouraged to:

1. Break down complex problems into smaller, more manageable parts.
2. Apply different mathematical techniques to find solutions.
3. Review and analyze the steps to ensure understanding and accuracy.

By using these strategies, students can effectively address even the most challenging problems, gaining deeper insights into the mathematical concepts behind them. Practicing regularly and reflecting on the methods used will lead to long-term improvement in problem-solving abilities.

Key Strategies for Solving CPM Problems

Successfully solving complex math problems requires a combination of strong problem-solving skills and effective strategies. By developing a structured approach to tackling exercises, students can improve both their accuracy and efficiency. The following strategies are designed to guide you through the problem-solving process and help you navigate difficult tasks with confidence.

Understand the Problem Thoroughly

The first and most important step in solving any problem is to understand exactly what is being asked. Carefully read through the problem, identifying key details such as variables, constraints, and what the solution is supposed to represent. By taking the time to understand the problem fully, you set a clear direction for solving it and avoid unnecessary mistakes.

Break the Problem into Manageable Parts

Complex problems often consist of multiple smaller tasks. Breaking down the problem into simpler, more manageable parts allows you to approach each step methodically. For example, if dealing with an equation, start by isolating one variable at a time or breaking the problem into smaller equations that are easier to solve. This approach helps in organizing your thoughts and prevents being overwhelmed by the complexity of the problem.

By applying these strategies, students can strengthen their problem-solving skills and become more effective in tackling challenging mathematical tasks. Practice and consistent application of these techniques will lead to greater success and understanding in the subject matter.

How to Interpret CPM Answer Key Solutions

When studying advanced mathematical problems, it’s important not only to seek solutions but also to understand the reasoning behind them. Interpreting provided solutions correctly allows you to learn the methods and techniques used to arrive at an answer. This skill is key to mastering problem-solving and improving overall mathematical proficiency.

Examine Each Step in the Solution

Each solution should be carefully analyzed, step by step. Start by looking at the initial approach and how the problem is framed. Break down each calculation, operation, or transformation applied throughout the solution process. This helps you identify which techniques were used and understand why they were necessary in solving the problem. By doing so, you gain insights into the thought process behind each step.

Compare and Apply the Techniques

Once you’ve reviewed the steps, compare them with your own attempts at solving the problem. If your method differs, consider why the solution uses a different approach or technique. This comparison allows you to learn from your mistakes and understand better ways to tackle similar problems in the future. Practice applying these techniques in various problems to reinforce your understanding and improve your skills.

By interpreting solutions in this detailed way, you not only learn the right answer but also grasp the fundamental problem-solving strategies that can be applied to a variety of tasks. This reflective approach will significantly enhance your math abilities.

Understanding the Structure of CPM Course 3

The structure of any educational program plays a crucial role in how students approach and absorb material. In this case, the program is designed to guide students through a series of progressively complex mathematical concepts, each building on the previous one. Understanding the flow and organization of the content will help learners navigate the topics more effectively, making their learning experience smoother and more successful.

Organized Learning Path

The curriculum is organized into distinct units, each focusing on a specific set of related concepts. These units are designed to flow logically, ensuring that foundational topics are covered first before progressing to more complex subjects. This structure ensures that students are not overwhelmed by difficult concepts and can build a solid understanding before moving on to more challenging material. Each section includes a mix of theory, problem-solving exercises, and real-world applications to reinforce the learning experience.

Interactive Approach to Learning

Throughout the program, students are encouraged to engage with the material actively. Rather than simply memorizing formulas or methods, learners are asked to apply concepts in various scenarios. This interactive approach helps to solidify understanding and develop critical thinking skills, making the learning process more dynamic and effective. Additionally, frequent assessments allow students to gauge their progress and identify areas where further study may be needed.

By understanding the structure and approach of the program, students can more effectively plan their study time and focus on mastering each topic as they move through the material. This methodical progression ensures that they are well-prepared for future challenges and can tackle more advanced mathematical concepts with confidence.

CPM Answer Key vs. Other Resources

When working through challenging mathematical problems, students often turn to a variety of resources to aid their understanding and improve problem-solving skills. While some may rely on specific solutions guides, others may seek out textbooks, online forums, or educational videos. Understanding the strengths and limitations of these different resources is crucial for making informed decisions about which one to use for assistance.

Comparison of Available Resources

Here’s a comparison of the most common types of resources used by students:

Resource	Advantages	Disadvantages
Solution Guides	Clear, step-by-step solutions; quick access to answers	Can encourage dependence on solutions instead of independent problem-solving
Textbooks	Comprehensive explanations; broad coverage of concepts	Can be lengthy; difficult to pinpoint specific solutions
Online Forums	Interactive discussions; real-time help from peers and experts	Quality of responses can vary; not always reliable
Educational Videos	Visual explanations; easy-to-follow examples	May not address all specific questions; can be time-consuming to find relevant content

Choosing the Right Resource

The key to effectively using any resource lies in selecting the right one for your current needs. Solution guides are great for checking your work or learning the correct method for solving a particular problem, but they should not replace the active learning process. Textbooks and videos can provide deeper explanations and are excellent for understanding theory, while online forums offer opportunities for discussion and clarification. Ultimately, combining multiple resources will give you the most well-rounded learning experience.

By understanding the differences between these resources, students can make informed choices that enhance their learning process, allowing them to solve problems more effectively and gain a deeper understanding of mathematical concepts.

Tips for Mastering CPM Math Problems

Successfully solving complex mathematical problems requires a mix of strategy, patience, and practice. While every student has their own approach, there are key techniques that can help improve problem-solving skills and increase efficiency. Mastering these methods will not only enhance understanding but also build confidence in tackling challenging exercises.

Key Strategies for Success

Here are some tips to help you approach math problems with more confidence and clarity:

• Understand the Basics: Before attempting to solve any problem, ensure you have a solid understanding of the foundational concepts. This will help you recognize patterns and choose the right approach for each task.
• Break Down the Problem: Large or complex problems can often seem overwhelming. Break them into smaller, manageable steps to focus on one part at a time. This makes the process less daunting and helps ensure accuracy.
• Use Visual Aids: Diagrams, charts, and graphs can be incredibly helpful in visualizing relationships between numbers and variables. Draw out the problem whenever possible to make abstract concepts more tangible.
• Practice Regularly: The more you practice, the more familiar you will become with different types of problems. Consistent practice allows you to recognize common patterns and improve problem-solving speed.
• Learn from Mistakes: Don’t be discouraged by errors. Review where you went wrong and understand why your solution didn’t work. Mistakes provide valuable lessons that improve your skills over time.

Utilizing Additional Resources

While self-study is important, seeking additional help can provide extra insight. Consider using supplementary resources such as online tutorials, study groups, or tutoring sessions to get a clearer understanding of challenging concepts. Discussing problems with peers can offer new perspectives and strengthen your grasp on the material.

By following these strategies and regularly practicing, you can improve your problem-solving abilities and approach math with greater confidence. Mastery comes with time and dedication, so stay committed to the process and continually challenge yourself to push further.

Addressing Common Mistakes in Course 3

Mathematical problem-solving can be tricky, and even experienced learners may encounter common pitfalls that hinder their progress. By understanding the frequent mistakes made during exercises, students can take steps to avoid them and improve their overall performance. Recognizing these errors allows for better comprehension and the development of effective strategies for success.

Frequent Mistakes to Avoid

Here are some common issues that often arise when solving math problems, along with tips for overcoming them:

• Misinterpreting the Problem: Many students jump into solving without fully understanding what the question is asking. Take time to read the problem carefully and identify the key information before proceeding with calculations.
• Skipping Steps: In a rush to find an answer, students sometimes skip intermediate steps, leading to errors. Always write down each step clearly, even if they seem simple, to ensure nothing is overlooked.
• Incorrect Application of Formulas: Using the wrong formula or applying it incorrectly is a common mistake. Always double-check the formula and confirm that it is appropriate for the specific problem.
• Relying Too Heavily on Memory: Memorizing formulas or methods without understanding the underlying principles can lead to mistakes. Focus on understanding the “why” behind the methods you use to develop a deeper understanding.
• Miscalculations: Simple arithmetic errors can throw off an entire solution. Always check your calculations carefully to minimize the chances of mistakes.

How to Improve Accuracy

To address these common mistakes, it’s essential to develop good habits. Here are some strategies for improving accuracy:

• Take Time to Understand the Problem: Before jumping to solutions, take a few moments to dissect the problem and ensure you understand what is being asked.
• Double-Check Your Work: After solving a problem, review your work step-by-step to identify any potential errors.
• Practice Regularly: The more you practice, the more familiar you become with common problem types, reducing the likelihood of making mistakes in the future.

By being mindful of these common errors and employing strategies to avoid them, students can strengthen their understanding and achieve more consistent success in their studies.

The Importance of Practice in CPM Courses

Consistent practice is essential to mastering mathematical concepts and improving problem-solving abilities. While understanding theory is important, the application of that knowledge through practice exercises is what truly solidifies learning and builds confidence. Working through various problems allows students to identify patterns, reinforce concepts, and develop strategies for tackling more complex tasks.

Engaging regularly with practice problems enhances retention and strengthens critical thinking skills. By approaching problems from different angles and with varying difficulty levels, students are better prepared for real-world applications and more advanced topics. Repetition not only fosters mastery but also helps learners internalize formulas and methods that become second nature over time.

Moreover, practice helps in identifying areas where additional focus is needed. Students may discover recurring challenges or gaps in understanding, which they can address proactively. This self-awareness plays a key role in effective learning, allowing individuals to refine their skills continuously.

How to Access CPM Answer Keys

Obtaining solutions to exercises in educational resources can be an essential part of the learning process. These resources help students verify their solutions, understand their mistakes, and reinforce their learning. However, it is important to access these solutions in a responsible and constructive manner, ensuring that they are used to enhance understanding rather than to simply copy answers.

Official Access Methods

There are several legitimate ways to gain access to these solutions, especially if you’re using official materials. Here are some common options:

• Student Portal: Many educational platforms offer an online portal where students can log in and access the necessary resources, including solutions for assignments and exercises.
• Instructor Resources: Teachers and instructors may provide access to solutions during class or through dedicated online platforms as part of the curriculum.
• Textbooks or Workbooks: Some textbooks include solutions at the back or provide companion workbooks that offer detailed solutions for the exercises.

Third-Party Resources

In addition to official sources, there are websites and platforms that offer solutions for a range of subjects. However, it’s essential to use these responsibly to ensure you’re using them for educational purposes:

• Online Forums: There are many forums where students share and discuss solutions. These can be helpful for clarification and understanding complex problems.
• Educational Websites: Some websites specialize in providing answers and step-by-step explanations for various educational programs. Always ensure these resources are reputable and accurate.

By using these methods, you can gain access to the necessary resources while maintaining an ethical and educational approach to your learning process.

Maximizing Your Learning with CPM Answers

Utilizing solutions effectively can greatly enhance your learning experience, especially when studying complex problems. It is essential to view these resources as tools for deeper understanding rather than shortcuts. By approaching them strategically, you can improve problem-solving skills and ensure long-term retention of mathematical concepts.

Effective Strategies for Using Solutions

Here are several strategies that can help maximize the value of these resources:

• Understand the Process: Rather than just reviewing the final result, focus on the step-by-step process used to arrive at the solution. This helps in grasping the underlying concepts and applying them in similar problems.
• Identify Mistakes: If you make errors while solving problems, use solutions to identify where you went wrong. Understand the mistake and the correct approach, which reinforces learning from errors.
• Work with Peers: Discussing solutions with classmates or study groups can provide different perspectives and enhance understanding. Collaboration helps uncover multiple methods to solve a problem.

Incorporating Solutions into Your Study Routine

Incorporating these resources into your study routine is crucial for maximizing their impact. Here are some tips to follow:

• Use Them as a Guide: Instead of using solutions as a crutch, treat them as a guide. Try solving the problem on your own first, then compare your method with the solution to refine your approach.
• Gradual Review: Don’t rely on solutions all at once. Review them gradually, ensuring you fully understand the reasoning behind each step and concept before moving to the next problem.
• Apply to New Problems: Practice similar problems after reviewing the solutions to apply what you’ve learned. This solidifies your understanding and helps you retain the information longer.

By following these strategies, you can turn solutions into a powerful tool for mastering the material and improving your problem-solving skills.