Calculus I Final Exam Answers and Study Guide

Preparing for a significant test in mathematics can be overwhelming, but with the right approach, you can tackle even the toughest questions. Understanding the core principles and practicing problem-solving techniques is essential to performing well. Whether you’re looking to solidify your grasp of complex functions or refine your skills in solving challenging equations, a strategic study plan will help you feel confident.
Structured review of important topics, combined with consistent practice, is one of the most effective ways to succeed. Focus on mastering the different types of problems you’ll encounter and identifying patterns that can help you approach new challenges with ease.
With the proper guidance and enough preparation, you will be equipped to manage the most difficult problems and apply your knowledge to real-world situations. Understanding the key methods and practicing them regularly will not only boost your performance but also give you the tools to excel.
Essential Topics for Calculus I Final
To excel in this critical assessment, it’s important to focus on key mathematical principles that form the foundation of the course. A solid understanding of these areas will not only help you solve complex problems but also allow you to approach any question with confidence.
Start by reviewing the fundamental concepts of limits and derivatives, as they are crucial to understanding the behavior of functions. Mastery of integration techniques and their applications is equally important, as this knowledge allows you to solve a wide range of problems effectively. Additionally, make sure to practice using series and sequences, as well as understanding their convergence.
Another essential area is the analysis of multivariable functions. Knowing how to work with partial derivatives, gradients, and optimization problems can be highly beneficial. Lastly, pay attention to the connections between different topics and how they are applied in real-world situations. A comprehensive understanding of these core subjects will ensure you are well-prepared for any challenges you might face.
Key Strategies for Exam Success
Achieving success in a challenging math assessment requires a combination of effective planning, time management, and focused practice. The right strategies can help you stay calm under pressure and tackle each question with clarity. By following a structured approach, you can maximize your performance and ensure that you are well-prepared for any obstacle.
- Start early: Give yourself enough time to review all relevant material. A consistent study routine over several weeks will help reinforce your understanding.
- Practice regularly: Work through sample problems and past questions to familiarize yourself with the types of challenges you’ll face. The more you practice, the more confident you’ll become.
- Identify key areas: Focus on the topics that are most commonly tested. Review core concepts and solve problems in these areas to ensure you’re prepared for a range of scenarios.
- Stay organized: Keep track of the concepts you’ve covered and the areas that need further attention. Break your study sessions into manageable chunks for better retention.
- Take breaks: Avoid burnout by scheduling short breaks during study sessions. Giving your brain time to rest will help you stay focused and improve retention.
- Simulate the testing environment: Try solving problems under timed conditions to practice working efficiently. This helps you manage your time effectively during the actual assessment.
By incorporating these strategies into your preparation, you’ll be able to approach the assessment confidently, minimize stress, and perform at your best.
Understanding Calculus I Exam Format
To approach any mathematical assessment effectively, it’s crucial to familiarize yourself with its structure. Knowing the format will help you prioritize your study efforts and develop the right strategies to tackle each section. By understanding the type of questions that will be asked and the time constraints, you can plan your preparation more efficiently.
- Question Types: The test typically consists of multiple-choice questions, short-answer problems, and long-form problems that require detailed solutions. Each section tests different aspects of mathematical understanding.
- Time Limits: Time management is essential. Ensure you allocate enough time to each section, keeping in mind that some problems may take longer to solve than others.
- Concept Application: Expect questions that require you to apply mathematical concepts to real-world scenarios, such as optimization problems or finding rates of change.
- Problem Difficulty: The questions may increase in difficulty as you progress through the assessment. Focus on mastering both simple and complex problems to ensure you’re ready for any challenge.
- Formula Usage: Some assessments provide a list of formulas, while others may expect you to memorize key equations. Be sure to practice using formulas efficiently and accurately under timed conditions.
Understanding these aspects of the assessment format will allow you to approach the test strategically, ensuring that you’re not only prepared but also confident in your ability to tackle a variety of question types. Proper preparation based on the format will lead to a smoother and more successful experience.
Tips for Effective Time Management
Managing your time efficiently during a challenging assessment is essential to ensure that you can complete all sections without unnecessary stress. With the right strategy, you can balance speed and accuracy, giving yourself enough time to carefully solve each problem. Being organized and deliberate with your time will help you maintain focus and maximize your performance.
- Plan Your Approach: Before starting, quickly skim through the entire test to get a sense of the difficulty and length of each section. Allocate your time based on the complexity of the questions.
- Start with Easy Problems: Begin with questions you feel most confident about to build momentum. This will give you a sense of accomplishment early on and help reduce anxiety.
- Set Time Limits: Break the test into smaller segments and set a timer for each section. This will prevent you from spending too much time on any one problem, ensuring you have enough time for the entire test.
- Avoid Overthinking: If you get stuck on a problem, move on and come back to it later. Spending too much time on a single question can affect your overall progress.
- Stay Calm: If you find yourself running out of time, stay calm and focused. Take a deep breath, prioritize the remaining problems, and finish as many as possible without rushing.
By implementing these strategies, you can ensure that your time is used wisely during the assessment. Effective time management will allow you to address each question thoroughly, without feeling rushed or overwhelmed.
Common Mistakes to Avoid in Calculus

While preparing for a challenging mathematics assessment, it’s crucial to be aware of common errors that can easily undermine your performance. Avoiding these pitfalls can help ensure that your understanding is accurately reflected in your solutions. Many of these mistakes stem from simple oversights, misinterpretations, or lack of attention to detail.
- Misapplying Formulas: Always double-check that you’re using the correct formula for the problem at hand. A small mistake in the formula can lead to incorrect results, even if your approach is otherwise sound.
- Skipping Steps: It’s tempting to skip intermediate steps, especially under time pressure. However, doing so can lead to errors or missed details that are crucial to finding the correct solution.
- Ignoring Units: When solving real-world problems, make sure you keep track of the units involved. Forgetting to convert or account for units can lead to confusing or incorrect answers.
- Overlooking Negative Signs: Pay close attention to the signs in your calculations. Neglecting negative signs in derivatives or integrals can drastically change the outcome of your solution.
- Rushing Through Word Problems: Carefully read word problems and identify all given information before jumping into the solution. Misinterpreting the problem can result in using the wrong method or missing key details.
- Failing to Check Work: After completing a solution, take a few moments to review your work. Double-check your calculations and ensure that your final answer makes sense in the context of the problem.
By being mindful of these common errors and taking the time to carefully work through each step, you can avoid unnecessary mistakes and improve your overall performance. Developing good habits and attention to detail will serve you well in any mathematical challenge.
Important Formulas for Your Exam
Knowing the essential mathematical formulas is key to solving problems efficiently and accurately. These equations are the building blocks of problem-solving and will allow you to apply concepts quickly during the assessment. By mastering these formulas, you can streamline your approach to even the most complex challenges.
- Derivative of Power Functions: For any function of the form f(x) = xⁿ, the derivative is given by f'(x) = n * xⁿ⁻¹. This rule is foundational for solving rates of change.
- Product Rule: When differentiating the product of two functions, use the formula: (f * g)’ = f’ * g + f * g’. This is essential for dealing with products in differentiation.
- Quotient Rule: For a function f(x) = g(x) / h(x), the derivative is f'(x) = (g'(x) * h(x) – g(x) * h'(x)) / h(x)². This helps in differentiating fractions of functions.
- Chain Rule: To differentiate composite functions, use the formula: (f(g(x)))’ = f'(g(x)) * g'(x). This rule is crucial when dealing with nested functions.
- Integral of Power Functions: For any function of the form f(x) = xⁿ, the integral is ∫xⁿ dx = (xⁿ⁺¹) / (n+1) + C, where C is the constant of integration. This is a basic rule for solving area under curves.
- Fundamental Theorem of Calculus: This theorem connects differentiation and integration, stating that ∫ from a to b of f(x) dx = F(b) – F(a), where F is the antiderivative of f.
- Integration by Parts: This technique is based on the formula ∫u dv = uv – ∫v du. It is useful for integrating products of functions.
Familiarizing yourself with these key formulas will save you valuable time and reduce the likelihood of errors during the assessment. Practice using them regularly, and you’ll gain a deeper understanding of how to apply each one effectively to various types of problems.
Step-by-Step Solutions for Calculus Problems
Solving mathematical challenges requires a structured approach to ensure clarity and accuracy. Breaking down problems into smaller, manageable steps helps prevent mistakes and improves understanding of the concepts involved. By following a systematic process, you can approach even the most complex questions with confidence.
Example Problem: Find the derivative of the function f(x) = 3x² + 5x – 2.
Step 1: Identify the terms
Start by recognizing each term in the function. In this case, we have three terms: 3x², 5x, and -2. Each term will be treated separately during the differentiation process.
Step 2: Apply the Power Rule
For each term, use the power rule for differentiation. The power rule states that if f(x) = xⁿ, then f'(x) = n * xⁿ⁻¹.
– For 3x², the derivative is 6x.
– For 5x, the derivative is 5.
– The derivative of a constant (-2) is 0.
Step 3: Combine the results
Now combine the derivatives of all the terms:
f'(x) = 6x + 5. This is the derivative of the function.
Step 4: Double-check your work
Go back and review your calculations. Ensure that you applied the correct rules to each term, and verify that the final result makes sense given the function’s structure.
By following these steps and applying the appropriate rules, you can confidently tackle similar problems and strengthen your problem-solving skills. Consistent practice with step-by-step solutions will not only enhance your ability to solve problems but also deepen your understanding of the concepts.
How to Review Calculus Effectively
Effective review is essential for reinforcing your understanding and ensuring you’re well-prepared for challenging assessments. Simply reading through notes or skimming textbooks isn’t enough. A focused, methodical approach to reviewing key topics will enhance your retention and help you apply concepts more confidently during problem-solving.
Organize Your Study Sessions
Start by identifying the most important areas to focus on. Organize your study time into blocks dedicated to specific topics. For example, dedicate one session to differentiation techniques and another to integration methods. This helps prevent feeling overwhelmed and ensures that each topic gets the attention it deserves.
Practice Regularly

The best way to solidify your understanding is through practice. Solve a wide variety of problems that cover different topics. The more problems you solve, the better you’ll understand the nuances of each concept. After solving problems, always review the solutions to understand your mistakes and correct them.
By structuring your review sessions and practicing consistently, you’ll improve both your theoretical knowledge and practical problem-solving skills. This targeted approach ensures you’re prepared for any challenge that arises during the test.
Practice Problems to Prepare For
To succeed in any challenging assessment, practicing a variety of problems is crucial. The more problems you solve, the better equipped you’ll be to tackle different types of questions and apply your knowledge effectively. By focusing on key problem types, you can strengthen your skills and gain confidence in your ability to perform well under pressure.
Types of Problems to Focus On
- Derivative Applications: Practice problems that require you to apply differentiation techniques, such as finding rates of change or solving optimization problems.
- Integration Techniques: Work on problems that involve finding areas under curves, calculating volumes, or solving indefinite integrals using various methods like substitution or integration by parts.
- Limits and Continuity: Solve problems that involve evaluating limits, determining the continuity of functions, and understanding the behavior of functions at critical points.
- Fundamental Theorem of Calculus: Focus on problems that require you to apply the fundamental theorem, connecting derivatives and integrals to solve real-world problems.
How to Approach Practice Problems

- Start with the basics: Begin with simpler problems to ensure you have a solid understanding of the core concepts before progressing to more difficult questions.
- Work on timed practice: Once you’re comfortable with the material, practice under timed conditions to simulate real test scenarios.
- Review solutions thoroughly: After solving each problem, carefully review your solutions and analyze any mistakes to understand where you went wrong and how to improve.
By practicing regularly and focusing on the key types of problems, you can sharpen your skills and ensure you’re well-prepared for any challenge that comes your way.
Breaking Down Difficult Concepts
Some mathematical ideas can seem overwhelming at first, but breaking them down into smaller, more manageable parts can make them much easier to understand. Complex topics often appear difficult because they require a solid grasp of basic principles, which need to be built upon step by step. By taking a structured approach, even the toughest concepts can be simplified and mastered.
Understanding Rates of Change: One of the most challenging aspects for many students is grasping how quantities change relative to each other. Whether it’s speed, acceleration, or growth rates, it’s important to break the concept down by looking at how small changes in one variable affect another. By focusing on incremental changes, you can gain a clearer picture of the overall behavior.
Mastering Area Under Curves: The idea of calculating areas under curves can be daunting, but it’s a matter of understanding how the curve behaves over a specific interval. Break it down into smaller steps: first, estimate areas using rectangles, then refine the estimate with more precise methods. Once you understand the basic idea, advanced methods like integration become much more intuitive.
Grasping Limits and Continuity: Understanding limits is essential to grasping how functions behave near particular points. Focus on interpreting what happens as a function approaches a certain value. Start with simple cases and gradually move to more complex situations. Once you’ve mastered limits, continuity becomes much clearer as you understand how functions behave across intervals.
By breaking down complex topics into understandable chunks, you’ll gain a deeper comprehension and feel more confident tackling even the most difficult problems. The key is to be patient, practice regularly, and never hesitate to revisit foundational concepts to build a strong understanding.
How to Handle Word Problems
Word problems can often seem intimidating, especially when they require you to translate a narrative into a mathematical equation. However, with the right approach, you can break down these problems step by step and make sense of the information presented. Understanding how to dissect a word problem is key to solving it effectively and efficiently.
Steps to Solve Word Problems
- Read the problem carefully: Begin by reading the problem slowly and highlighting important information. Pay close attention to any numbers, units, and specific details mentioned in the text.
- Identify what is being asked: Determine the final goal of the problem. Are you asked to find a rate of change, an area, or a volume? Knowing what you need to solve for helps you focus your efforts.
- Translate the problem into mathematical terms: Once you’ve understood the narrative, translate it into an equation or system of equations. This might involve identifying variables and recognizing which mathematical operations to use.
- Solve step by step: Break the problem into smaller parts. Solve each part sequentially, ensuring you don’t skip any steps. It’s often helpful to use a diagram or a table to organize the information.
- Double-check your solution: After solving, revisit the problem to ensure that your answer makes sense in the context of the situation. Verify the units and the reasonableness of your result.
Common Pitfalls to Avoid
- Skipping the translation step: Always make sure to express the problem in mathematical terms before proceeding to solve it. Skipping this step can lead to confusion or incorrect solutions.
- Overlooking key information: Word problems often include extraneous details that can be distracting. Focus only on the information that’s relevant to the question being asked.
- Rushing through the calculations: Take your time with the math. Rushing can lead to mistakes, especially when working with complex equations or multiple steps.
By following a systematic approach and practicing regularly, you’ll become more confident in handling word problems. The key is to stay organized, focus on key details, and work through each problem methodically.
Maximizing Your Study Time

Effective time management is crucial when preparing for any academic challenge. By organizing your study sessions efficiently, you can ensure that you cover all necessary material while also allowing time for review and practice. Maximizing your study time involves prioritizing key areas, eliminating distractions, and maintaining a steady pace throughout your preparation.
Strategies for Productive Study Sessions

- Set clear goals: Before each study session, define specific objectives. Whether it’s mastering a particular concept or completing a set of practice problems, knowing your goals helps you stay focused.
- Break your study time into intervals: Use techniques like the Pomodoro Method, where you study for 25 minutes followed by a 5-minute break. This helps maintain concentration and prevents burnout.
- Prioritize difficult topics: Start with the most challenging material when your mind is fresh. Tackling harder concepts early on allows for more time to work through them without feeling rushed.
- Review regularly: Consistent review is essential for retaining information. Set aside time at the end of each week to go over previously covered material to reinforce your knowledge.
- Practice actively: Focus on solving problems and applying concepts rather than just reading through notes. Active engagement with the material helps you better understand and retain it.
Tips to Avoid Common Study Pitfalls

- Avoid multitasking: Focusing on multiple things at once can reduce the quality of your study session. Stay committed to one task at a time to improve efficiency.
- Eliminate distractions: Find a quiet space and turn off your phone or any notifications that could interrupt your concentration.
- Don’t cram: Avoid last-minute cramming, as it is ineffective for long-term retention. Consistent, spaced-out study sessions are more beneficial.
By following these strategies, you can make the most of your study time and prepare more effectively for the upcoming challenges. The key is to stay organized, manage your time wisely, and ensure that you’re actively engaging with the material each day.
Real-World Applications of Calculus
The concepts studied in mathematical analysis are not just theoretical; they have practical uses in many fields that impact our daily lives. From optimizing business operations to understanding natural phenomena, the ability to model and solve real-world problems is one of the greatest strengths of mathematical theory. Below are some of the most common applications where these concepts are put to use:
| Field | Application | Example |
|---|---|---|
| Physics | Motion analysis | Determining the velocity and acceleration of moving objects |
| Economics | Optimization of profits | Maximizing revenue by finding the optimal production level |
| Engineering | Structural analysis | Designing buildings and bridges by analyzing forces and stresses |
| Biology | Population modeling | Predicting population growth or decay based on birth and death rates |
| Medicine | Drug dosage modeling | Determining the right dosage for medications over time |
These examples demonstrate how mathematical tools are essential in various industries, helping solve complex problems by providing insight into dynamic systems. The ability to analyze change and model systems is crucial for innovation, efficiency, and advancement in many domains.
Using Graphs to Solve Calculus Questions
Visualizing mathematical problems through graphs is an essential tool for understanding the behavior of functions and their relationships. Graphs help make abstract concepts more tangible by providing a clear picture of how variables interact. By interpreting graphical data, one can derive solutions to a variety of problems, such as finding areas under curves, understanding rates of change, and optimizing functions. This approach makes it easier to grasp complex ideas and solve problems more efficiently.
Key Graphical Concepts
When using graphs to solve problems, it is important to understand several key concepts, including:
- Slope: The rate of change of a function, often represented by the tangent line at a specific point.
- Area under the curve: Used for problems involving total accumulation, such as distance traveled over time.
- Critical points: Points where the slope is zero, often indicating local maxima or minima.
- Concavity: The curvature of the graph, which can indicate whether a function is increasing or decreasing at an accelerating rate.
Graphical Tools for Problem-Solving
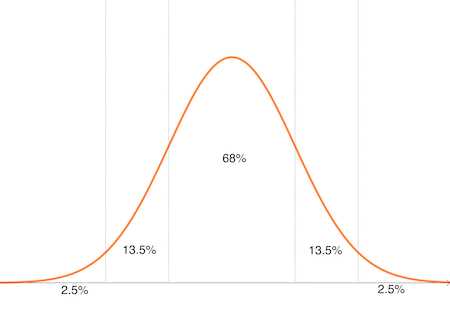
Different types of graphs and their specific properties can be applied to solve various types of questions:
| Graph Type | Application | Example Problem |
|---|---|---|
| Line Graph | Used to show linear relationships and rates of change. | Determining the slope of a straight line representing speed over time. |
| Parabola | Represents quadratic functions and can be used to find maximum or minimum values. | Finding the vertex of a parabola to determine the maximum profit. |
| Exponential Curve | Used for modeling growth or decay, such as population increase or radioactive decay. | Calculating the population growth after a certain period. |
| Sine Wave | Useful in periodic functions, such as sound waves or seasonal changes. | Determining the amplitude of a wave or the frequency of oscillations. |
By utilizing these graphical techniques, one can more effectively analyze functions and solve related problems. Graphs make it easier to identify key points, interpret results, and verify solutions, providing a visual approach to problem-solving that is both intuitive and powerful.
Understanding Limits and Continuity
In mathematical analysis, the concepts of approaching values and smoothness are fundamental in understanding how functions behave. These ideas are crucial for determining how a function behaves near certain points, and whether it can be described without sudden jumps or breaks. By studying how values tend to a particular number as the input changes, one can gain insights into the function’s overall behavior. Continuity refers to the property of a function where small changes in the input result in small changes in the output, without any interruptions.
Limits: The Foundation of Behavior

The limit is a central concept that helps determine the value a function approaches as the input gets closer to a specific point. A limit does not necessarily mean the function reaches that value at the point itself, but rather that it gets arbitrarily close as the input approaches that point.
- Approaching a finite value: As the input approaches a certain number, the output gets closer to a specific value.
- Approaching infinity: Sometimes, the output grows without bound, as the input increases or decreases.
- One-sided limits: Limits can be taken from one direction only, from the left or the right, which can affect the function’s behavior.
Continuity: Smoothness of Functions
Continuity describes a function that has no gaps, jumps, or asymptotes at a given point. A function is continuous if its graph can be drawn without lifting the pencil, meaning the function does not have any sudden breaks or discontinuities.
- Continuous at a point: A function is continuous at a specific point if the limit at that point exists and equals the function’s value.
- Types of discontinuities: Functions can have jump discontinuities, infinite discontinuities, or removable discontinuities, which represent different kinds of behavior when the function is not continuous.
Understanding limits and continuity provides the tools to analyze functions in-depth, predicting their behavior near certain points and identifying smooth or abrupt changes in their structure.
Integration Techniques for Your Preparation
Mastering the process of finding areas under curves is essential for understanding complex functions. Several techniques exist that allow for the simplification of such problems, enabling one to break down seemingly complicated integrals into more manageable components. These methods rely on recognizing patterns, applying substitution, and using powerful theorems to reduce the complexity of the problem. Whether it’s by recognizing standard forms or using advanced tricks, mastering these strategies will help you handle any integral you encounter.
Common Integration Techniques
Here are some essential techniques to consider when tackling integration problems:
| Method | Description |
|---|---|
| Substitution | When a function contains a composite function, substitution allows you to simplify the integral by changing variables. |
| Integration by Parts | This technique is based on the product rule and is particularly useful for integrals involving products of functions. |
| Partial Fractions | Used for breaking down rational functions into simpler fractions that are easier to integrate. |
| Trigonometric Substitution | Helpful when dealing with integrals that involve square roots of quadratic expressions. |
| Improper Integrals | Applied when integrating over an infinite range or dealing with discontinuities within the limits. |
Choosing the Right Method
Choosing the correct method depends on the form of the function you’re integrating. Identifying the underlying structure of the integral is key to deciding whether substitution, integration by parts, or another method should be applied. Practice recognizing patterns and getting comfortable with each technique to increase your efficiency and accuracy during problem-solving.
By refining these methods, you will be well-equipped to tackle any challenging integral that comes your way. Practice is the key to mastering these techniques and ensuring a smooth solving process when it matters most.