Final Exam Review Geometry Answers for Success

final exam review geometry answers

As you prepare for the most important assessment of your course, it’s essential to focus on the core principles that will guide your problem-solving skills. Understanding the fundamental ideas will allow you to approach each task with confidence, breaking down complex questions into manageable steps.

During your preparation, make sure to revisit key principles that are commonly tested. Whether it’s working with shapes, calculating areas, or applying rules for various transformations, practicing regularly will help solidify your understanding. Use diagrams and visual aids to better grasp these concepts, as they can often make abstract ideas much clearer.

Effective study strategies should include both practice problems and a review of important formulas. Regularly testing yourself will help you identify areas that need more attention, while reinforcing your strengths. It’s also important to develop a systematic approach, ensuring that each problem is tackled methodically and with precision.

Lastly, don’t forget to manage your time effectively. It’s not only about knowing the material, but also about staying calm and focused under pressure. With the right approach, you can maximize your potential and achieve great results.

Mastering Key Geometry Concepts for Finals

final exam review geometry answers

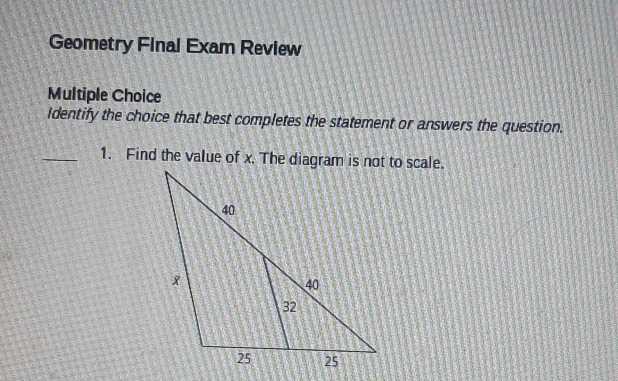
To succeed in your upcoming test, it’s crucial to master the foundational ideas that will support your ability to solve problems efficiently. A solid understanding of the underlying principles enables you to approach challenges with clarity and precision. Whether dealing with measurements, shapes, or spatial relationships, honing these concepts will give you the confidence to tackle any question that comes your way.

Focus on the most commonly tested topics, such as properties of different shapes, the relationships between angles, and methods of calculating areas and volumes. These areas often form the basis of many questions, so having a clear grasp of their key features will allow you to work through problems quickly and accurately.

In addition to theoretical knowledge, develop the ability to apply this knowledge to practical situations. For instance, practice visualizing problems and drawing out diagrams. This not only helps in understanding the relationships between various components but also provides a clearer path to solving them. Being able to recognize patterns and use them effectively will significantly improve your problem-solving abilities.

Finally, review the most important theorems and rules that apply to the different types of figures and transformations. Knowing when and how to apply these principles will save you time and prevent unnecessary mistakes. Consistent practice and a methodical approach will be key to mastering these concepts and achieving success on your assessment.

Essential Geometry Formulas to Remember

When preparing for assessments in this subject, having a strong grasp of key formulas is crucial. These equations are the building blocks that allow you to calculate important values quickly and accurately. Whether dealing with shapes, angles, or measurements, understanding the essential formulas will streamline your problem-solving process.

Basic Area and Perimeter Formulas

Knowing how to calculate areas and perimeters is fundamental. Here are some of the most important formulas to remember:

Rectangle: Area = length × width, Perimeter = 2(length + width)
Circle: Area = π × radius², Circumference = 2π × radius
Triangle: Area = 1/2 × base × height, Perimeter = sum of all sides
Square: Area = side², Perimeter = 4 × side

Volume and Surface Area Formulas

final exam review geometry answers

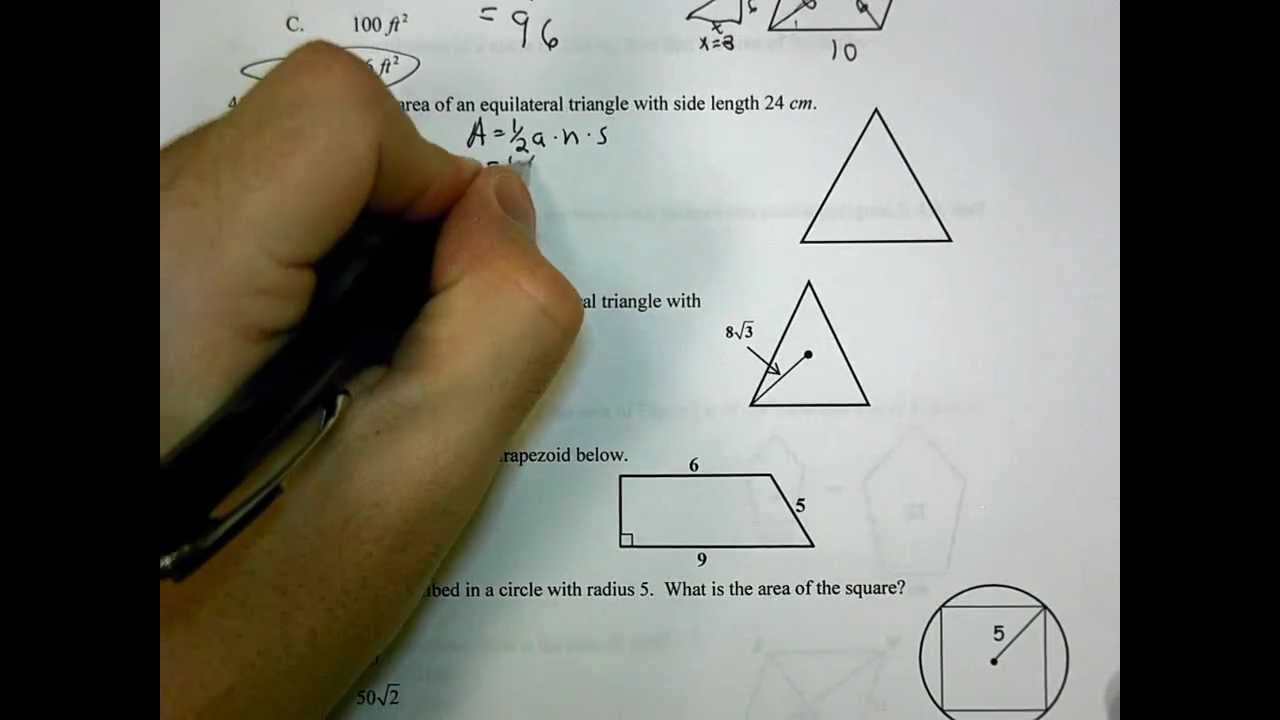
For three-dimensional figures, knowing how to calculate volume and surface area is equally important. Here are the key formulas:

Cube: Volume = side³, Surface Area = 6 × side²
Cylinder: Volume = π × radius² × height, Surface Area = 2π × radius × (height + radius)
Sphere: Volume = 4/3 × π × radius³, Surface Area = 4π × radius²
Rectangular Prism: Volume = length × width × height, Surface Area = 2(length × width + width × height + height × length)

Memorizing these formulas will save you time and effort during assessments, allowing you to focus on applying the correct principles to each problem. Practice using these formulas regularly to build familiarity and confidence in their application.

How to Tackle Geometry Word Problems

Word problems can often feel intimidating, but they are simply a way to test your ability to apply learned concepts in real-world scenarios. The key to solving these problems is to break them down into manageable steps, ensuring that you understand what is being asked and how to approach the situation methodically. With a clear strategy, any problem can be solved with confidence.

Step 1: Read and Understand the Problem

Before diving into calculations, read the problem carefully. Pay attention to the details such as measurements, shapes, and relationships between different elements. Identify the known values and what the problem is asking for. Highlight or underline important information to help focus your attention on the key points.

Step 2: Visualize the Problem

One of the most effective ways to solve word problems is to create a diagram. Draw a picture of the situation, labeling the important points, lines, and angles. This will make it easier to see relationships and apply the correct formulas. Visualizing the problem often reveals new insights and can make complex problems more manageable.

Step 3: Choose the Right Approach

Based on the diagram and the given information, decide which formulas or theorems are most appropriate. Whether it’s using the Pythagorean theorem, properties of similar triangles, or area and volume formulas, be sure to select the most effective method for the situation. If multiple methods are possible, choose the one that is most straightforward to avoid unnecessary complications.

Step 4: Solve and Check Your Work

Once you’ve applied the necessary formulas, solve for the unknown values. After completing the calculations, check your answer against the problem to ensure it makes sense. If the result doesn’t align with the context of the problem, revisit your steps to identify any errors in reasoning or arithmetic.

Common Mistakes to Avoid in Geometry

While working through problems, it’s easy to make small errors that can have a big impact on your results. Recognizing these common mistakes is key to improving your performance. By being aware of where people tend to go wrong, you can avoid making the same errors and ensure more accurate solutions.

Misreading the Problem: Often, people rush through word problems or overlook important details. Always read the question thoroughly and make sure you understand what is being asked before proceeding.
Incorrect Use of Formulas: Applying the wrong formula or using a formula incorrectly can lead to significant mistakes. Double-check which formula is appropriate for the situation before starting your calculations.
Forgetting Units of Measurement: It’s important to pay attention to the units provided in the problem. Sometimes students forget to convert units or leave them out altogether, which can lead to incorrect results.
Overlooking Diagrams: Diagrams are often provided to help visualize the problem. Don’t skip over them; ensure that you understand the relationships shown in the diagram and use it to inform your solution.
Neglecting to Check Work: Rushing through the process without reviewing your calculations is a common mistake. Always double-check your steps to confirm that your final solution is accurate.

Being mindful of these common pitfalls and taking the time to carefully approach each problem will help you avoid mistakes and increase your accuracy. By consistently practicing these good habits, you can improve your overall problem-solving ability.

Geometry Review Tips for Better Results

Effective preparation is not just about working through problems–it’s about working smart. To achieve the best possible results, you need a strategy that enhances understanding and improves retention. By focusing on key strategies, you can streamline your study process and make the most of your time.

1. Focus on Core Concepts

Instead of memorizing everything, concentrate on the fundamental principles that form the foundation for most problems. Understanding core concepts such as shapes, angles, and spatial relationships will allow you to approach any question with confidence, even if it’s presented in a new way.

2. Practice with Purpose

Don’t just complete random problems. Choose exercises that cover a variety of topics and gradually increase in difficulty. This will help reinforce concepts and build your problem-solving skills. Consistent, targeted practice leads to stronger retention and quicker application of knowledge.

3. Use Active Recall

Rather than passively reviewing notes or textbooks, actively quiz yourself on key concepts and formulas. Write down everything you remember and check for accuracy. This method improves long-term memory retention and helps you identify any gaps in understanding.

4. Teach Someone Else

Explaining concepts to someone else, even if they don’t know the material, forces you to simplify and clarify your thoughts. This method is a powerful tool for reinforcing your own understanding and identifying areas that may still need work.

5. Manage Your Time Effectively

Effective time management is crucial when preparing. Break down your study sessions into focused intervals (e.g., 25-minute blocks) followed by short breaks. This keeps you fresh and ensures sustained focus, allowing you to cover more material without burning out.

By incorporating these strategies into your study routine, you’ll improve both your understanding and performance. Consistency, practice, and focused effort are the keys to success. Stay disciplined, stay organized, and results will follow.

How to Use Diagrams Effectively in Exams

Diagrams are a powerful tool that can simplify complex problems and make relationships between different elements clearer. When faced with a question, don’t just look at the numbers and formulas–take a moment to visualize the situation. This can guide you toward the right solution and help you organize your thoughts more effectively.

Step 1: Draw a Clear Diagram

The first step is always to sketch a neat and accurate diagram of the situation described in the problem. Label all given information clearly, such as lengths, angles, or other relevant details. Even if the problem already provides a diagram, drawing your own version can help solidify your understanding and ensure no details are overlooked.

Step 2: Use the Diagram to Identify Relationships

final exam review geometry answers

Once your diagram is in place, use it to identify important relationships between the elements. Look for symmetry, parallel lines, right angles, and other key properties. These can often provide insights that help you choose the right formulas and strategies to solve the problem.

Step 3: Mark Important Points and Values

As you work through the problem, continue to update the diagram with new information or findings. Mark angles, intersections, or midpoints as needed. This helps you keep track of the relationships and ensures you apply the correct values when calculating solutions.

Step 4: Check Your Work Using the Diagram

Finally, use the diagram to double-check your results. Does your solution make sense given the visual layout? If something feels off, revisiting the diagram can often reveal errors or provide new insights that lead to the correct answer.

By using diagrams strategically, you can clarify complex problems, avoid mistakes, and improve your problem-solving efficiency. Take time to visualize before jumping into calculations–it’s a small step that can lead to big improvements in your results.

Quick Tricks for Geometry Problem Solving

When it comes to solving complex problems, having a few tricks up your sleeve can make all the difference. These quick methods help streamline the process, allowing you to arrive at solutions more efficiently. With the right techniques, you can reduce the time spent on each question and increase your chances of solving even the trickiest problems.

Here are some quick strategies that can be applied to a variety of problems:

Trick	Description	Example
Use Symmetry	If a shape exhibits symmetry, you can often deduce unknown values by reflecting or rotating parts of the figure.	For a symmetrical quadrilateral, if one side is known, the opposite side is the same length.
Draw Auxiliary Lines	Adding extra lines, such as altitudes or medians, can create simpler triangles and help you apply theorems more easily.	In a right triangle, drawing an altitude from the vertex to the hypotenuse splits the triangle into two smaller right triangles.
Recognize Special Triangles	Some triangles have special properties that can save you time. For example, 30-60-90 and 45-45-90 triangles have predictable ratios.	In a 30-60-90 triangle, the sides are in the ratio 1:√3:2, making it easier to find missing lengths.
Use the Pythagorean Theorem	Whenever you see a right triangle, remember the Pythagorean theorem. This can help you solve for missing sides quickly.	If the legs of a right triangle are 3 and 4, the hypotenuse is 5, as 3² + 4² = 5².
Look for Proportions	If two triangles are similar, corresponding sides are proportional, allowing you to set up equations to solve for unknowns.	If two triangles have sides in the ratio 3:4, and one side of the larger triangle is 12, the corresponding side in the smaller triangle is 9.

By incorporating these tricks into your problem-solving process, you can approach each question with more confidence and efficiency. Remember, practice is key to mastering these techniques, so be sure to apply them regularly in your study sessions.

Understanding Geometry Proofs for Success

Proofs are a fundamental aspect of problem-solving, requiring logical reasoning to demonstrate the truth of a statement. Rather than simply memorizing steps, it’s important to develop a deep understanding of how to build a coherent argument. Mastering the art of constructing proofs not only strengthens your logical thinking but also helps you approach complex problems with clarity and confidence.

Step 1: Understand the Given Information

Before starting a proof, carefully review the information provided in the problem. Identify all known facts, such as given lengths, angles, or properties of shapes. These form the foundation of your proof and will guide your reasoning throughout the solution process.

Step 2: Build Your Logical Argument

A proof is essentially a series of logical statements leading from the given information to the desired conclusion. Start by applying known theorems, postulates, or definitions that directly relate to the problem. As you progress, each step should follow logically from the previous one, ensuring that your argument is sound and coherent.

Use Diagrams: Visual aids can often clarify relationships and help you visualize the logical flow of your proof. Draw and label any necessary diagrams to support your argument.

Keep Track of Your Steps: Write out each step clearly, explaining why it follows from the previous one. This not only helps you stay organized but also makes it easier to spot mistakes or gaps in your reasoning.

By approaching proofs with a systematic strategy, you’ll develop the skills necessary to construct clear and convincing arguments. This methodical approach is key to success and will help you solve more advanced problems in the future.

Geometry Theorems You Must Know

Understanding key theorems is essential for solving many problems in mathematics. These principles not only provide the foundation for logical reasoning but also serve as shortcuts to finding solutions quickly and accurately. Here are some critical theorems that you should know and understand for effective problem-solving.

Theorem	Description	Application
Pythagorean Theorem	This theorem relates the sides of a right triangle, stating that the square of the hypotenuse is equal to the sum of the squares of the other two sides.	Use it to find missing sides of a right triangle when two sides are known. Example: a² + b² = c².
Congruence Postulates	These postulates (SSS, SAS, ASA, AAS) are used to prove that two triangles are congruent based on the equality of their sides or angles.	Apply these when you need to prove that two triangles are identical in size and shape.
Angle Sum Theorem	The sum of the interior angles of any triangle is always 180 degrees.	This helps find missing angles in triangles, especially when given two angles.
Isosceles Triangle Theorem	If two sides of a triangle are equal, the angles opposite those sides are also equal.	Use this theorem when working with isosceles triangles to identify or solve for unknown angles.
Parallel Lines Theorem	When a transversal crosses two parallel lines, the alternate interior angles are congruent, and the consecutive interior angles are supplementary.	Use this to solve problems involving parallel lines and angles formed by a transversal.
Exterior Angle Theorem	The exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.	Helpful for solving problems involving exterior angles of triangles and determining missing angle measures.

Mastering these theorems allows you to approach problems more efficiently and confidently. By recognizing the situations where these principles apply, you can simplify complex questions and find solutions more quickly. Make sure to practice these theorems regularly to reinforce your understanding and improve your problem-solving skills.

Effective Time Management During Geometry Exams

Proper time management is crucial when tackling complex problems under time constraints. Without a clear plan, it’s easy to become overwhelmed and lose focus. By managing your time wisely, you can ensure that you complete all parts of the test and have time to double-check your work. Developing a strategic approach is essential for performing well and maximizing your score.

Step 1: Plan Your Time

Before starting, take a moment to quickly glance over the entire test and assess the time allotted. Divide the total time by the number of questions to get an idea of how long to spend on each one. If some questions appear more difficult than others, adjust your plan to allow more time for those. Make sure to keep track of time during the test, and if necessary, set small goals to stay on track.

Step 2: Prioritize and Tackle Easy Questions First

Begin by answering the questions you find easiest. This allows you to secure quick points and boosts your confidence. Once you’ve completed the simpler questions, move on to the more challenging ones. If you encounter a particularly tough problem, don’t get stuck on it for too long–move on and return to it later if time allows. This strategy ensures that you don’t waste valuable time on one question.

By following a structured time management plan, you can approach each problem strategically, ensuring that you complete the test efficiently. Practicing this method in mock tests will help you become more comfortable with pacing yourself and reduce anxiety during the real test.

Geometry Test Strategies for Students

Success in any assessment requires more than just understanding the material. It also involves strategic planning, focus, and effective techniques to manage the test. With the right approach, students can increase their efficiency and accuracy, ensuring they complete each section confidently and within the time limit.

Here are some essential strategies to help you perform at your best:

Start with the Familiar: Begin by tackling the questions that seem easiest. This allows you to secure points early and boosts your confidence for the more challenging problems ahead.
Understand the Instructions: Carefully read all the instructions and questions. Misinterpreting a question can lead to unnecessary mistakes. Ensure you fully understand what is being asked before you begin solving.
Use Process of Elimination: For multiple-choice questions or questions with several options, use the process of elimination to narrow down the choices. Rule out clearly wrong answers to increase your chances of selecting the correct one.
Keep Track of Time: Make a quick plan for how long you should spend on each question. Avoid spending too much time on any one problem, and don’t hesitate to move on if you’re stuck. You can always return to difficult questions later.
Show Your Work: Always write down your steps, even if you can solve the problem in your head. This will help you catch mistakes and make it easier to recover if you make an error. Additionally, if partial credit is awarded, showing your process can help you earn points.
Stay Calm and Focused: Anxiety can lead to mistakes. Keep calm and take deep breaths if you start to feel overwhelmed. Staying focused and composed is essential for maintaining clarity throughout the test.
Double-Check Your Answers: If time allows, review your answers before submitting. Look for calculation errors, overlooked details, or missing steps. Even a small mistake can lead to a loss of points, so take the extra time to ensure everything is correct.

By incorporating these strategies into your test-taking routine, you’ll be able to approach each question with a clear plan, manage your time efficiently, and increase your overall performance. Practice these techniques to become more comfortable with the testing environment and improve your results over time.

Reviewing Transformations in Geometry

Transformations are key concepts that help you understand how shapes change and interact within a coordinate plane. These operations manipulate figures in various ways, such as moving, rotating, reflecting, and resizing them. Mastering these principles is essential for solving problems that involve spatial relationships and properties of shapes.

Here’s an overview of the main types of transformations you should be familiar with:

Translation: This involves moving a shape from one location to another without changing its size, shape, or orientation. It’s often described by a vector, indicating how far and in what direction the shape moves.
Reflection: Reflection flips a shape over a line, creating a mirror image. The line of reflection acts like a “mirror,” and the distances between corresponding points and the line of reflection are always equal.
Rotation: A rotation turns a shape around a fixed point, known as the center of rotation. The angle of rotation tells you how far the shape is turned, and the direction (clockwise or counterclockwise) indicates which way the shape spins.
Dilation: Dilation changes the size of a figure, either enlarging or reducing it, while keeping its shape the same. This transformation is defined by a center of dilation and a scale factor that determines the size change.

Understanding how to apply these transformations is crucial for solving problems that involve symmetry, congruence, or similarity. When working with transformations, it’s helpful to keep track of key properties such as distances, angles, and orientation, as these may change or remain the same depending on the type of transformation. Practice using these concepts in different scenarios to reinforce your understanding and improve your ability to solve complex problems.

Geometry Problems with Coordinates Explained

When working with shapes and figures in a coordinate plane, understanding how to interpret and solve problems involving coordinates is crucial. These problems often require you to apply distance, midpoint, and slope formulas, as well as to analyze geometric properties based on their position in the plane. Mastering these concepts will help you efficiently tackle a variety of problems that involve the spatial relationships between points, lines, and shapes.

Here are some key concepts and strategies to help you solve problems involving coordinates:

Distance Formula: This formula is used to find the distance between two points in the plane. The formula is derived from the Pythagorean theorem and is written as:

Distance = √((x₂ - x₁)² + (y₂ - y₁)²)

Apply this to find the length of a line segment or the distance between two points.
Midpoint Formula: The midpoint of a line segment is the point that is exactly halfway between the two endpoints. The formula is:

Midpoint = ((x₁ + x₂)/2, (y₁ + y₂)/2)

Use this when you need to find the coordinates of the midpoint between two given points.
Slope Formula: The slope of a line measures its steepness and direction. The formula to find the slope between two points is:

Slope = (y₂ - y₁) / (x₂ - x₁)

This is essential for determining if two lines are parallel, perpendicular, or neither.
Equation of a Line: Once you have the slope, you can use the point-slope form or slope-intercept form to write the equation of a line:

y - y₁ = m(x - x₁) (point-slope form) or y = mx + b (slope-intercept form).

These are useful for solving problems involving lines and intersections.
Collinearity: To determine if three or more points are collinear (lie on the same straight line), calculate the slopes between pairs of points. If the slopes are equal, the points are collinear.

By mastering these key formulas and strategies, you’ll be able to solve coordinate-based problems more efficiently and with greater accuracy. Practice applying these concepts to different scenarios to strengthen your skills and build confidence when working with coordinate geometry.

How to Study Geometry Efficiently

Effective study habits are essential for mastering complex concepts and excelling in spatial reasoning tasks. To study efficiently, it’s important to organize your learning, practice regularly, and focus on areas that challenge you the most. By following a structured approach, you can enhance your understanding and retain critical information for solving problems effectively.

Step 1: Master Key Concepts

Start by focusing on the foundational principles that form the basis of many problems. This includes understanding shapes, angles, transformations, and basic formulas. A solid grasp of these core concepts will make solving more complex problems easier and faster. Take the time to review definitions, properties, and theorems, and try to visualize them using diagrams. The more you understand the “why” behind each concept, the better you’ll be able to apply it in various contexts.

Step 2: Practice Regularly

Consistent practice is crucial to becoming proficient. Work through a variety of problems, from basic exercises to more challenging scenarios, to strengthen your problem-solving skills. Use practice tests and online resources to simulate test conditions. Focus on problems that test multiple concepts, as this will help you integrate your knowledge and prepare for any question format. Don’t hesitate to go over problems you find difficult multiple times until you fully understand the solution process.

By breaking your study time into manageable chunks, staying organized, and dedicating time to both practice and understanding, you will gradually build the skills and confidence needed to succeed. Tracking your progress and regularly reviewing key concepts will also help solidify your knowledge and prepare you for more advanced material.

Practice Problems and Solutions

One of the most effective ways to prepare for any assessment is through practice. By working through various problems, you reinforce your understanding and improve your ability to apply concepts under time pressure. In this section, you will find a selection of practice problems along with step-by-step solutions. These will help you build confidence and identify any areas where further review may be needed.

Problem 1: Distance Between Two Points

Problem: Find the distance between the points (3, 4) and (7, 1).

Solution: Use the distance formula:

Distance = √((x₂ - x₁)² + (y₂ - y₁)²)

Substitute the given points (x₁, y₁) = (3, 4) and (x₂, y₂) = (7, 1):

Distance = √((7 - 3)² + (1 - 4)²) = √(16 + 9) = √25 = 5

The distance between the points is 5 units.

Problem 2: Slope of a Line

Problem: Calculate the slope of the line passing through the points (2, 3) and (4, 7).

Solution: Use the slope formula:

Slope = (y₂ - y₁) / (x₂ - x₁)

Substitute the given points (x₁, y₁) = (2, 3) and (x₂, y₂) = (4, 7):

Slope = (7 - 3) / (4 - 2) = 4 / 2 = 2

The slope of the line is 2.

Problem 3: Equation of a Line

Problem: Find the equation of the line that passes through the point (1, 2) and has a slope of 3.

Solution: Use the point-slope form of the equation of a line:

y - y₁ = m(x - x₁)

Substitute the given slope m = 3 and the point (x₁, y₁) = (1, 2):

y - 2 = 3(x - 1)

Expand and simplify:

y - 2 = 3x - 3 y = 3x - 1

The equation of the line is y = 3x - 1.

By practicing problems like these, you’ll gain a deeper understanding of key concepts and improve your ability to solve similar problems quickly and accurately.