AP Calculus AB Review Packet Answers and Solutions

Preparing for the AP exam in higher-level mathematics requires a deep understanding of the core principles and problem-solving techniques. This section is designed to guide you through the most essential topics, providing a structured approach to mastering complex concepts. By focusing on key strategies and examples, you’ll gain confidence in applying mathematical theories to a wide range of problems.

In this guide, we will break down critical areas of the curriculum, helping you tackle even the most challenging questions with ease. From functions and rates of change to integration techniques, each topic will be approached in a way that encourages both conceptual understanding and practical application.

Whether you are reviewing specific sections or reinforcing foundational knowledge, the goal is to ensure you’re well-equipped to face the exam. By practicing with diverse problems and sharpening your skills, you’ll be prepared to navigate the test efficiently and effectively.

AP Calculus AB Review Packet Answers

This section is designed to help you navigate through complex mathematical problems and understand the essential concepts needed to excel on the AP exam. By exploring different types of problems and their solutions, you will gain the skills required to approach each question methodically and with confidence. The following explanations provide a structured approach to mastering the material and strengthening your problem-solving abilities.

Understanding Key Problem Types

To succeed in the exam, it’s important to be familiar with the various types of questions you’ll encounter. These range from evaluating limits to applying derivative rules and solving integration problems. Each problem requires a different set of strategies, and understanding these strategies is crucial for success. By breaking down each problem into its fundamental components, you can more easily identify the most efficient approach to solve it.

Tips for Effective Practice

Practice consistently to reinforce your understanding. Focus on the most commonly tested topics and make sure you’re comfortable with their applications. Solve problems step by step and review any mistakes carefully to understand where your reasoning went wrong. With dedicated practice, you’ll build the confidence needed to tackle the toughest questions on the exam.

Understanding the Key Concepts in AP Calculus

Mastering the fundamental principles of advanced mathematics is essential for success on the AP exam. This section will focus on the core ideas that serve as the foundation for solving complex problems. Grasping these concepts will not only help you understand how to approach each question but also allow you to recognize the underlying patterns that frequently appear on the exam.

Key topics to focus on include:

• Limits and Continuity: Understanding the behavior of functions as they approach specific values.
• Derivatives: Learning how to calculate the rate of change and the slope of a curve at any point.
• Integrals: Mastering the techniques for finding areas under curves and solving accumulation problems.
• Applications of Derivatives: Exploring real-world problems such as optimization and motion analysis.
• Fundamental Theorem of Calculus: Connecting the concepts of integration and differentiation.

By focusing on these core topics, you can build a solid foundation that will make solving more complicated problems easier. With consistent practice, you’ll gain confidence and develop the problem-solving strategies needed to excel in the exam.

Step-by-Step Solutions for AP Problems

When tackling complex problems on the AP exam, a clear and structured approach is crucial. This section will guide you through the process of breaking down difficult questions into manageable steps, ensuring that each solution is reached methodically. Understanding each stage of problem-solving is key to applying the right techniques and achieving accurate results.

Here is an example of a step-by-step approach to solving a typical problem:

Step	Description
1	Identify the given information and understand the problem statement.
2	Determine the method or formula required to solve the problem.
3	Substitute the known values into the appropriate formula or equation.
4	Simplify and calculate the result step by step.
5	Check the result and ensure it makes sense in the context of the problem.

By following these steps, you can approach each question systematically and confidently, ensuring a higher level of accuracy and efficiency in your responses.

Breaking Down Common Calculus AB Questions

In preparation for the AP exam, it’s important to recognize the most frequently encountered types of problems and understand how to solve them effectively. This section will help you break down typical questions into manageable components, enabling you to apply the appropriate techniques with confidence. By focusing on key areas that often appear on the exam, you can approach each problem with a clearer strategy.

Problem 1: Evaluating Limits

One of the most common question types involves evaluating limits. These questions require you to determine the value that a function approaches as its input approaches a specific point. Key steps to solving these include simplifying the function, applying limit properties, and identifying any indeterminate forms that require special techniques such as L’Hopital’s Rule.

Problem 2: Derivatives and Rates of Change

Another frequent topic involves finding derivatives, which measure the rate of change of a function at a particular point. To approach these questions, begin by applying differentiation rules such as the power rule, product rule, or chain rule. Pay close attention to the function’s behavior and interpret the result in the context of the problem.

By understanding how to approach these common types of questions, you can tackle even the most complex problems with a clear, step-by-step strategy.

Essential Formulas for AP Success

Having a solid understanding of the key formulas and concepts is crucial for mastering advanced mathematics. In this section, we will highlight the most important formulas that frequently appear on the AP exam. By familiarizing yourself with these essential tools, you can efficiently solve a wide range of problems and improve your performance on the test.

Here are some of the most important formulas to remember:

• Derivative Rules:
  • Power Rule: ( frac{d}{dx}x^n = nx^{n-1} )
  • Product Rule: ( frac{d}{dx}(u cdot v) = u’v + uv’ )
  • Quotient Rule: ( frac{d}{dx}left(frac{u}{v}right) = frac{v cdot u’ – u cdot v’}{v^2} )
• Integration Formulas:
  • Power Rule for Integration: ( int x^n dx = frac{x^{n+1}}{n+1} + C )
  • Fundamental Theorem of Integration: ( int_a^b f(x) dx = F(b) – F(a) )
• Limit Properties:
  • Limit of a Sum: ( lim_{x to c} (f(x) + g(x)) = lim_{x to c} f(x) + lim_{x to c} g(x) )
  • Limit of a Product: ( lim_{x to c} (f(x) cdot g(x)) = lim_{x to c} f(x) cdot lim_{x to c} g(x) )

By mastering these key formulas, you can approach each problem with a clear strategy and solve it effectively. Remember, practice is essential to internalize these formulas and apply them accurately during the exam.

How to Tackle Derivatives in AP Calculus

Understanding how to find the rate of change of a function is a fundamental skill required to solve a wide range of problems on the AP exam. This section will guide you through the process of calculating derivatives, providing clear strategies for handling different types of functions. By mastering these techniques, you’ll be able to approach derivative questions with confidence and accuracy.

To effectively tackle these problems, follow these steps:

• Identify the Function: Start by clearly identifying the function you are differentiating. Look for any compositions or products that might require special rules.
• Choose the Correct Rule: Depending on the form of the function, apply the appropriate derivative rule. This could include the power rule, product rule, quotient rule, or chain rule.
• Simplify Step by Step: After applying the rules, simplify the expression carefully. Double-check your calculations to ensure no mistakes were made in the process.
• Interpret the Result: Once you have the derivative, think about what it represents. This could indicate the slope of a curve, the rate of change, or other key characteristics of the function.

By following this methodical approach, you can confidently solve derivative problems and apply them to real-world scenarios. With practice, these steps will become second nature, helping you solve problems more efficiently during the exam.

Exploring Limits and Continuity in Calculus

Understanding the behavior of functions at specific points is essential for solving complex problems in advanced mathematics. Limits and continuity form the foundation for many key concepts and problem-solving techniques. This section will provide an overview of how to approach and analyze limits and the conditions that determine whether a function is continuous or discontinuous.

When examining limits, it is important to focus on the behavior of a function as the input approaches a specific value. Continuity, on the other hand, deals with whether the function behaves smoothly without jumps, breaks, or holes.

The table below summarizes key concepts for solving problems related to limits and continuity:

Concept	Description	Example
Limit	The value that a function approaches as the input gets closer to a specific point.	lim(x>3) (x? – 9)/(x – 3)
Continuity	A function is continuous if there are no interruptions (jumps, holes, or asymptotes) at a given point.	f(x) = 1/(x – 2) is discontinuous at x = 2.
Indeterminate Forms	Expressions like 0/0 that require further manipulation, such as L’Hopital’s Rule, to evaluate limits.	lim(x>0) (sin(x)/x) = 1

By understanding how to apply these concepts, you can solve a wide range of problems involving limits and continuity. Practice with different types of functions will help you become more adept at analyzing their behavior in various scenarios.

Understanding Integrals and Their Applications

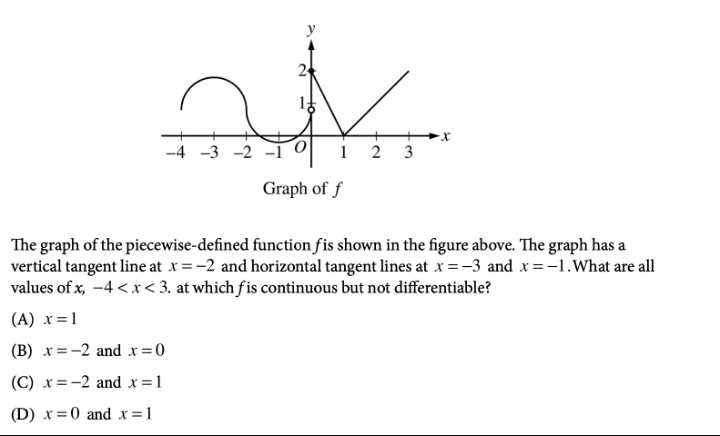
Integrals are essential tools in advanced mathematics, helping to solve problems related to accumulation, area under curves, and total change. This section delves into the concept of integration, exploring its fundamental principles and how it is applied to various real-world situations. Whether you’re calculating areas, solving differential equations, or analyzing motion, integrals provide the framework to address these challenges.

Key Concepts in Integration

• Definite Integrals: These represent the accumulation of quantities over a specific interval. They are often used to calculate the area under a curve.
• Indefinite Integrals: These express the general form of a function’s antiderivative and include a constant of integration.
• Fundamental Theorem of Integration: This theorem connects differentiation and integration, stating that the derivative of an integral is the original function.

Applications of Integrals

Integrals have a wide range of practical applications. Below are some of the key areas where integration is used:

• Finding Areas: Integrals are commonly used to calculate the area under curves, such as the area between a graph and the x-axis.
• Solving Motion Problems: Integration is used to determine the distance traveled by an object over time by integrating its velocity.
• Modeling Accumulated Quantities: Integrals help model the total accumulated change, such as the total work done or total energy used in a system.

Understanding these concepts and applying them effectively is key to solving integration problems on the AP exam. With practice, you can use integrals to handle complex problems with precision and clarity.

Mastering the Fundamental Theorem of Calculus

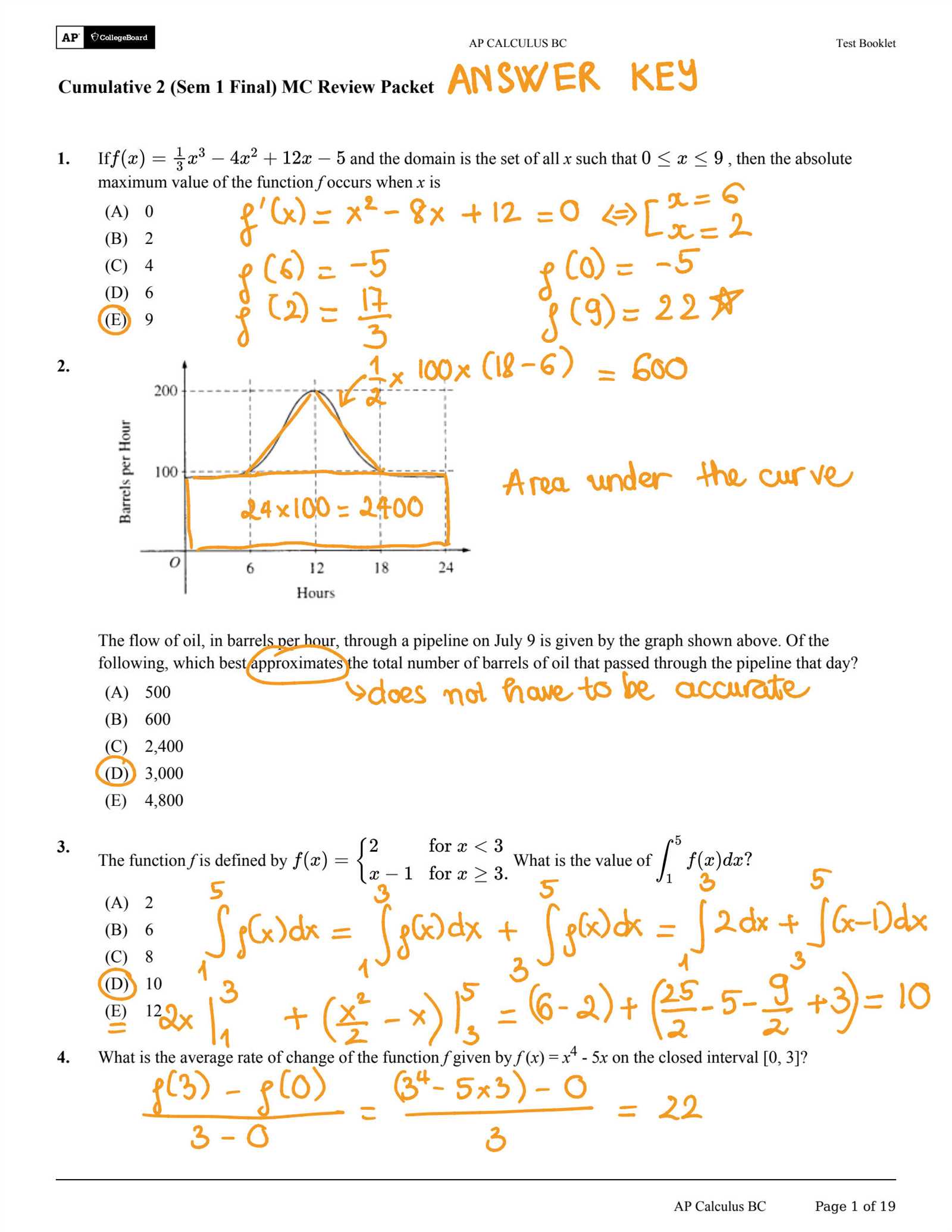
The Fundamental Theorem of Integration is a cornerstone of advanced mathematics. It bridges the concepts of differentiation and integration, showing how they are interconnected. This theorem is essential for solving many types of problems, as it allows you to evaluate integrals efficiently by understanding the relationship between the rate of change and accumulation of quantities. Mastery of this concept is key to simplifying complex problems and developing a deeper understanding of mathematical functions.

Key Ideas Behind the Theorem

At its core, the theorem states that differentiation and integration are inverse operations. This means that, in a sense, integrating a function undoes the process of differentiation, and vice versa. The Fundamental Theorem is divided into two parts:

• Part 1: It establishes that if a function is continuous on a closed interval, the integral of that function over the interval can be computed using its antiderivative.
• Part 2: It states that if you have a function and its antiderivative, the derivative of the integral of that function is simply the original function.

Applications and Techniques

Understanding and applying this theorem can greatly simplify the process of evaluating integrals. Here are some techniques that rely on the Fundamental Theorem:

• Evaluating Definite Integrals: If you have the antiderivative of a function, you can evaluate the definite integral by simply plugging in the upper and lower bounds.
• Solving Area Problems: The theorem is essential for calculating areas under curves, as it provides a direct method to compute such areas through integration.

By mastering the Fundamental Theorem of Integration, you’ll be able to approach integration problems with more confidence and efficiency, ensuring you are well-prepared for the AP exam.

Common Mistakes to Avoid on the AP Exam

As you prepare for the AP exam, it’s crucial to be aware of common pitfalls that can negatively impact your performance. Many students fall into the trap of rushing through problems or misinterpreting the wording of questions. By recognizing these common mistakes, you can improve your approach and avoid unnecessary errors on test day.

Key Mistakes to Watch Out For

• Misunderstanding Question Requirements: Be sure to carefully read each question and understand what is being asked. Some questions may have subtle wording that requires a specific approach or interpretation.
• Rushing Through Calculations: Speed is important, but accuracy is even more critical. Take the time to work through each problem step by step and double-check your calculations before submitting your answers.
• Neglecting Units and Notation: Always include proper units in your answers where required. In many cases, leaving out units or using incorrect notation can result in losing valuable points.

How to Prevent These Mistakes

• Practice Time Management: During your practice sessions, simulate exam conditions to improve your time management skills. This will help you become more efficient during the actual test without compromising the quality of your work.
• Review Your Work: If time allows, review your answers at the end of the exam to ensure there are no careless errors. Even small mistakes, like sign errors or missing steps, can cost points.
• Focus on Key Concepts: Make sure you have a solid understanding of the main principles that are tested. Often, it’s not about memorizing formulas but knowing when and how to apply them correctly.

By staying mindful of these common mistakes and taking proactive steps to avoid them, you can greatly improve your chances of performing well on the AP exam. Careful preparation and a clear understanding of the material are key to success.

Time-Saving Tips for AP Review

Efficient preparation is key when tackling complex subjects, especially when facing an exam with limited time. By implementing a few time-saving strategies, you can streamline your study sessions, focus on what matters most, and maximize your performance without feeling overwhelmed. The following tips will help you study smarter, not harder, and make the most of your review time.

Focus on High-Yield Topics

To make the best use of your time, prioritize the topics that are most frequently tested. Instead of trying to cover every single concept in the syllabus, concentrate on mastering the core principles that form the foundation of many questions. Key areas often include:

• Derivative Rules and Techniques
• Definite and Indefinite Integrals
• Fundamental Theorem of Integration
• Application of Rates of Change

Use Practice Problems Wisely

One of the most effective ways to prepare efficiently is by practicing problems that mimic the structure of the exam. Focus on solving problems that align with the most common types of questions you are likely to encounter. Here are some strategies for maximizing the benefit of your practice:

• Target Weak Areas: Identify and focus on the areas where you’re struggling the most, but don’t neglect to review the topics you’re already comfortable with.
• Timed Practice: Set time limits when solving practice problems to simulate exam conditions. This will help you improve your speed and accuracy.
• Review Mistakes: After completing practice exercises, carefully go through the errors to understand where you went wrong. This will help you avoid making the same mistakes on the actual exam.

By focusing on high-yield topics and using practice problems effectively, you can reduce the time spent on unnecessary review and ensure you’re prepared to tackle the exam with confidence.

Strategies for Multiple-Choice AP Questions

Multiple-choice questions can be challenging, especially when you’re faced with complex problems and tight time constraints. However, with the right approach, you can improve your chances of selecting the correct answers. In this section, we’ll explore some strategies to help you navigate these questions efficiently and confidently.

One key to mastering multiple-choice questions is understanding how to quickly identify the most likely solutions and rule out incorrect options. Often, these questions will contain distractors designed to test your understanding of subtle concepts or common misconceptions. Knowing how to approach these questions strategically will allow you to maximize your score while minimizing the time spent on each one.

Here are a few techniques to apply during the exam:

• Process of Elimination: Always start by eliminating obviously incorrect answers. This increases your chances of guessing correctly if you need to make an educated guess. The fewer options left, the easier it becomes to spot the right answer.
• Look for Key Words: Pay attention to terms that often appear in the correct answers, such as “always,” “never,” or “most likely.” These words can provide hints about the answer’s accuracy.
• Check Units and Notation: When possible, use logical reasoning or check the units in the question to help narrow down the possible answers. Often, dimensional analysis or basic unit conversion can point you toward the correct option.
• Skip and Return: If you’re stuck on a particular question, skip it and return to it later. Sometimes, answering other questions first can jog your memory or help you gain insights into the trickier questions.

By applying these strategies during your exam, you can improve your ability to answer multiple-choice questions quickly and accurately, allowing you to focus your energy on the more complex parts of the test.

Effective Ways to Practice for the AP Exam

Preparing for the AP exam requires a focused and strategic approach. Rather than cramming large amounts of information at the last minute, it’s more effective to engage in consistent practice that reinforces core concepts and improves problem-solving skills. The key is to approach your study sessions with a clear plan, focusing on high-yield areas and using various methods to ensure comprehensive understanding.

One of the most powerful ways to practice is by regularly solving problems that resemble the types of questions you’ll face during the exam. This will help you get comfortable with the format, timing, and complexity of the questions. Additionally, reviewing your mistakes is an essential part of learning. Identifying and understanding where you went wrong helps to solidify your knowledge and avoid repeating the same errors in the future.

Here are several effective methods to incorporate into your practice routine:

• Simulate Test Conditions: Practice solving problems under timed conditions to get used to the pressure of the actual exam. This will help you manage your time effectively on test day.
• Use Past Exam Papers: Working through past AP exams gives you a clear understanding of the types of questions asked and allows you to familiarize yourself with the exam’s pacing.
• Focus on Weak Areas: Identify topics where you struggle the most and dedicate extra time to them. Reviewing these areas ensures you don’t leave gaps in your knowledge.
• Mix Up the Question Types: Don’t focus only on one type of question–practice a variety of problems, including multiple-choice, free-response, and conceptual questions to build well-rounded skills.
• Review and Reflect: After completing each practice session, thoroughly review your answers, especially the ones you got wrong. Understanding why you made a mistake and how to avoid it in the future is crucial for improvement.

By integrating these practices into your study routine, you’ll develop a deeper understanding of the material and build the confidence needed to succeed on the AP exam. Consistency, focus, and strategic review are the keys to effective preparation.

Using Graphing Calculators in AP Calculus

Graphing calculators are an essential tool for many students preparing for the AP exam. These devices help visualize mathematical concepts, solve complex equations, and explore functions in ways that would be difficult to achieve manually. When used effectively, a graphing calculator can save time and reduce the complexity of certain problems, allowing students to focus on the core ideas rather than getting bogged down in lengthy calculations.

While calculators are a helpful aid, it’s important to understand their limitations and use them strategically. The goal is not to rely on the calculator for every step, but to use it as a supplement for tasks that require visual representation, like graphing functions or finding numerical approximations. Mastering how to use these tools efficiently can give you a significant advantage during the exam.

Key Uses of Graphing Calculators

• Visualizing Functions: Graphing calculators can help you quickly plot functions, which is useful for understanding their behavior, identifying asymptotes, and visualizing limits or continuity.
• Finding Derivatives and Integrals: Calculators can perform symbolic differentiation and integration, allowing you to quickly check your work or gain insights into more complicated problems.
• Solving Equations: Graphing calculators can solve equations numerically and graphically, helping to find solutions where algebraic methods are too cumbersome or impractical.
• Working with Limits: Many graphing calculators allow you to examine the behavior of functions near certain points, providing a visual understanding of limits and helping to confirm your solutions.

Maximizing the Benefit of Your Calculator

To make the most of your graphing calculator, it’s crucial to familiarize yourself with its functionality before the exam. Take the time to practice with it, especially when it comes to graphing functions, solving equations, and finding key features like critical points, intercepts, and inflection points. Also, review any calculator-specific techniques that can help save time, such as shortcut keys and menus for advanced operations.

Remember, the calculator should be used as a tool to support your understanding of the material–not as a crutch. It’s important to develop a strong grasp of the underlying principles so that you can confidently interpret the results from your calculator and apply them correctly in the context of the exam.

Reviewing Key Theorems and Their Proofs

Understanding key theorems and their proofs is fundamental to mastering the concepts needed for the AP exam. Theorems serve as the backbone of mathematical reasoning, offering powerful tools to solve problems efficiently and understand complex relationships between different concepts. In this section, we focus on some of the most important theorems, breaking them down and highlighting their proofs, which provide the logical foundation for solving a variety of problems.

While it is essential to know the statements of these theorems, it’s equally important to grasp their proofs. By understanding the logic behind each theorem, students are better equipped to apply them in different contexts, whether solving equations, finding derivatives, or analyzing functions. These proofs offer insight into why certain techniques work, and mastering them strengthens your problem-solving skills and deepens your understanding of the subject.

The Fundamental Theorem of Calculus

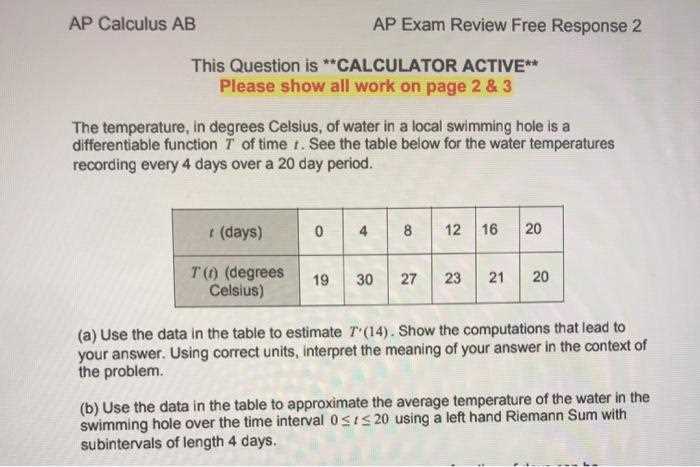
The Fundamental Theorem of Calculus connects differentiation and integration, two primary operations in mathematics. It states that if a function is continuous over an interval and differentiable on that interval, then the integral of its derivative over that interval is equal to the difference in the function’s values at the endpoints. This theorem not only provides the foundation for solving integral problems but also helps in interpreting the relationship between rates of change and accumulated quantities.

Mean Value Theorem

The Mean Value Theorem establishes a connection between the instantaneous rate of change and the average rate of change of a function over a given interval. It states that for any continuous and differentiable function, there exists at least one point where the instantaneous rate of change equals the average rate of change over the interval. Understanding this theorem allows students to make predictions about the behavior of a function and is often applied in real-world contexts such as physics and economics.

By reviewing these core theorems and their proofs, students can reinforce their problem-solving strategies and gain a deeper understanding of mathematical relationships. The ability to apply these results accurately is crucial for success on the AP exam and in future studies in mathematics and related fields.

AP Exam Preparation Checklist

Preparing for the AP exam requires a well-structured approach, focusing on key areas of the subject and ensuring that all essential topics are reviewed and understood. Having a checklist can help streamline your study sessions, track progress, and make sure that you are well-prepared for every section of the test. Below is a detailed preparation guide to help you stay organized and efficient in the weeks leading up to the exam.

Key Topics to Master

It is crucial to focus on the core topics that are frequently tested. These include the following:

• Understanding the relationship between rates of change and accumulation of quantities.
• Mastering techniques for finding derivatives and integrals.
• Practicing applications of optimization and area problems.
• Reviewing key theorems and their proofs for deeper understanding.
• Strengthening your knowledge of limits and continuity.

Time Management and Strategy

Time management during your study sessions and on the actual exam is vital for success. Use these tips to maximize efficiency:

• Set aside consistent time blocks each day for focused studying.
• Practice solving problems under timed conditions to simulate the test environment.
• Prioritize areas where you feel less confident and spend extra time reviewing those concepts.
• Take regular breaks to avoid burnout and stay sharp throughout your preparation.

By following this checklist and focusing on the critical topics and strategies, you’ll be able to maximize your chances of success. Whether you’re revisiting foundational concepts or practicing advanced problems, consistent preparation will pay off on exam day.