Factoring Day 2 Worksheet Answers Explained
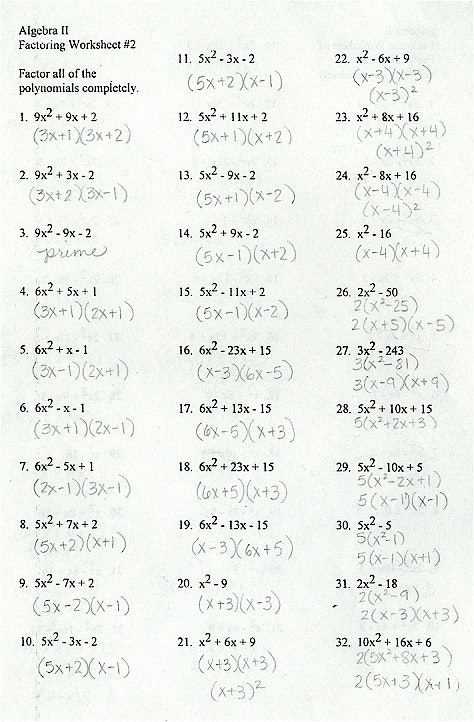
In this section, we explore essential methods for breaking down complex mathematical expressions. These techniques are foundational for solving a variety of algebraic problems, helping to simplify and solve equations with ease. Understanding the key concepts covered here will provide you with the tools needed to tackle increasingly difficult challenges.
Developing a deep understanding of these strategies not only enhances your problem-solving skills but also strengthens your overall grasp of algebra. By applying these techniques effectively, you can quickly identify solutions to problems and gain confidence in your ability to work through mathematical tasks.
Throughout this guide, we will focus on explaining each step clearly, with practical examples to solidify your knowledge. With continuous practice, the process will become second nature, allowing you to approach algebraic problems with a structured mindset.
In this section, we explore essential methods for breaking down complex mathematical expressions. These techniques are foundational for solving a variety of algebraic problems, helping to simplify and solve equations with ease. Understanding the key concepts covered here will provide you with the tools needed to tackle increasingly difficult challenges.
Developing a deep understanding of these strategies not only enhances your problem-solving skills but also strengthens your overall grasp of algebra. By applying these techniques effectively, you can quickly identify solutions to problems and gain confidence in your ability to work through mathematical tasks.
Throughout this guide, we will focus on explaining each step clearly, with practical examples to solidify your knowledge. With continuous practice, the process will become second nature, allowing you to approach algebraic problems with a structured mindset.
Understanding the Basics of Factoring

At the core of many algebraic techniques lies the ability to break down complex expressions into simpler components. This process involves recognizing patterns and relationships within terms that allow us to simplify equations, making them easier to solve. A solid understanding of these foundational principles is crucial for progressing in algebraic problem-solving.
Identifying Common Patterns
The first step in mastering these methods is learning to identify common patterns in expressions. Whether dealing with polynomials or quadratic forms, recognizing the structure of the terms involved can significantly reduce the complexity of the problem. By understanding how different terms relate to each other, one can apply specific techniques to simplify them effectively.
Applying Basic Techniques

Once the patterns are identified, the next step is to apply the appropriate methods to decompose the expression. This involves rewriting the terms in a way that reveals their factors, making it easier to solve for unknowns or find solutions. The more familiar one becomes with these techniques, the quicker and more accurately they can approach different types of algebraic problems.
Key Concepts Covered on Day 2
In this section, we dive into the essential principles that build the foundation for solving algebraic expressions. The focus is on recognizing patterns, applying core strategies, and refining skills that are pivotal for progressing to more complex problems. Each concept plays a vital role in simplifying and solving equations efficiently.
- Recognizing Binomial Patterns – Understanding how to identify common binomial forms and their components is crucial for simplifying expressions and solving for unknowns.
- Breaking Down Quadratic Equations – Learn how to manipulate and decompose quadratic equations, making them easier to solve through various algebraic methods.
- Working with Common Factors – Identify and factor out the greatest common factor (GCF) to simplify expressions before proceeding with further steps.
- Using Special Polynomials – Understanding specific polynomial forms, such as perfect square trinomials and difference of squares, and how to handle them effectively.
By mastering these concepts, you will gain the tools needed to solve problems with greater ease and precision, allowing for smoother progression through algebraic challenges.
How to Approach Factoring Problems
When faced with algebraic challenges, it’s important to have a clear and structured approach to simplify the process. The key is to break down complex expressions into more manageable components by identifying relationships between terms. This method helps in finding solutions efficiently and with greater confidence.
The first step is always to look for common factors across terms. Whether it’s a numerical factor or a variable, isolating the greatest common factor (GCF) can simplify the expression significantly. After this, carefully examine the structure of the remaining terms to see if they fit any well-known patterns, such as the difference of squares or perfect square trinomials.
Next, apply the appropriate technique based on the structure of the equation. If dealing with quadratics, consider using methods like splitting the middle term or using trial and error to find the correct pair of factors. With practice, recognizing which approach to take becomes quicker and more intuitive.
Finally, double-check your work to ensure the solution is correct. This step may involve expanding the factored form to verify that it matches the original expression. Careful attention to each detail will help avoid mistakes and ensure that your approach remains solid for more complex problems ahead.
Step-by-Step Solutions for Factoring

Breaking down complex algebraic expressions into simpler forms requires a systematic approach. By following a clear sequence of steps, each part of the problem becomes easier to manage. This method ensures accuracy and provides a solid foundation for solving more advanced equations in the future.
The first step is to identify the greatest common factor (GCF) of all terms. If possible, factor it out to simplify the equation. This reduces the complexity of the problem and makes it easier to handle the remaining terms. Once the GCF is removed, examine the structure of the remaining expression.
Next, look for recognizable patterns within the remaining terms. Common patterns such as the difference of squares, perfect square trinomials, or simple binomials should be identified. For example, a quadratic expression might split into two binomials, making it easier to find the solution.
Once the appropriate pattern is recognized, apply the relevant method to decompose the expression. This could involve techniques like splitting the middle term, trial and error, or using special formulas. After the expression is factored, always check the result by multiplying the factored terms back together to ensure they match the original equation.
Common Mistakes in Factoring
While simplifying algebraic expressions, it’s easy to make certain errors that can lead to incorrect results. Understanding and avoiding these mistakes is essential for mastering the process and achieving accurate solutions. Many errors stem from overlooking patterns or misapplying techniques, which can be prevented with careful attention to detail.
Overlooking the Greatest Common Factor
One of the most common mistakes is forgetting to factor out the greatest common factor (GCF) at the beginning. This step is crucial for simplifying the expression before applying other techniques. If the GCF is ignored, the remaining terms may become unnecessarily complicated, making the problem harder to solve.
Incorrectly Splitting the Middle Term
When breaking down quadratic expressions, an incorrect split of the middle term is another frequent error. It’s important to ensure that the numbers chosen multiply to give the correct product and add up to the correct sum. Mistakes in this step can result in an incorrect factorization, which will not solve the problem accurately.
By being mindful of these common pitfalls and practicing the correct methods, you can significantly reduce errors and improve your algebraic skills.
Importance of Factoring in Algebra

Breaking down complex expressions into simpler forms is a vital skill in algebra, enabling easier manipulation and solution of equations. This technique serves as a foundation for understanding more advanced mathematical concepts and is essential for solving a wide range of problems, from basic equations to real-world applications.
Mastering this process allows students to approach algebraic challenges with confidence. It transforms complicated equations into more manageable pieces, making it easier to isolate variables and solve for unknowns. Whether simplifying polynomials, solving quadratic equations, or handling higher-level expressions, this skill is indispensable.
Furthermore, this method plays a crucial role in various fields, including engineering, physics, and economics. By understanding how to decompose expressions, one can better analyze patterns, predict outcomes, and solve practical problems more efficiently. It’s clear that this technique is not only foundational in academic algebra but also has real-world value in analytical thinking and problem-solving.
Tips for Mastering Factoring Techniques
Developing a strong understanding of algebraic simplification techniques requires consistent practice and attention to detail. With the right strategies, mastering these methods becomes a more intuitive and rewarding process. These tips will help you refine your approach and improve your problem-solving efficiency.
First, it’s essential to practice identifying common patterns in expressions. Recognizing these patterns early allows you to apply the right technique quickly and accurately. Whether it’s a binomial or trinomial, knowing what to look for can save time and reduce mistakes.
Second, work through step-by-step examples to strengthen your skills. Breaking down complex problems into smaller, manageable steps is key to mastering any technique. The more problems you solve, the more proficient you become at recognizing the best approach for each type of expression.
| Tip | Description |
|---|---|
| Start with the GCF | Always check for the greatest common factor (GCF) first to simplify the expression. |
| Look for patterns | Identify familiar forms like perfect squares or differences of squares to simplify your work. |
| Check your work | Always verify your factored form by multiplying it back to ensure accuracy. |
| Use trial and error | For more complex expressions, use trial and error to find factors that fit. |
By consistently applying these strategies, you’ll gradually develop a deeper understanding and a more efficient approach to solving algebraic expressions.
Factoring Challenges and How to Overcome Them
While simplifying algebraic expressions can seem straightforward, it often comes with its share of difficulties. The key to overcoming these obstacles lies in recognizing patterns, applying appropriate methods, and maintaining a systematic approach. Understanding common challenges can help you navigate through problems more effectively.
One frequent challenge is identifying the correct approach when faced with a new problem. Some expressions may not immediately fit familiar forms, making it difficult to know where to start. In these cases, taking the time to break the expression into smaller parts and checking for common factors or patterns can help clarify the best method to use.
Another obstacle is making arithmetic mistakes during the process of simplifying or splitting terms. Small errors in basic multiplication or addition can lead to incorrect solutions. To avoid this, always double-check your calculations and, if necessary, work through the problem slowly to ensure accuracy at each step.
Finally, losing track of the structure of the expression can result in missed solutions. Sometimes, the key to solving a problem is recognizing the right pattern or relationship between terms. Practice and familiarity with various forms of equations will improve your ability to spot these connections more quickly and accurately.
Applying Factoring to Real-Life Problems
Algebraic simplification techniques are not just academic exercises–they can be applied to solve real-world problems. By breaking down complex situations into manageable parts, these methods help in analyzing patterns, optimizing solutions, and making decisions based on mathematical reasoning. Understanding how to apply these methods in everyday contexts makes their value clear beyond the classroom.
Optimizing Business and Financial Decisions
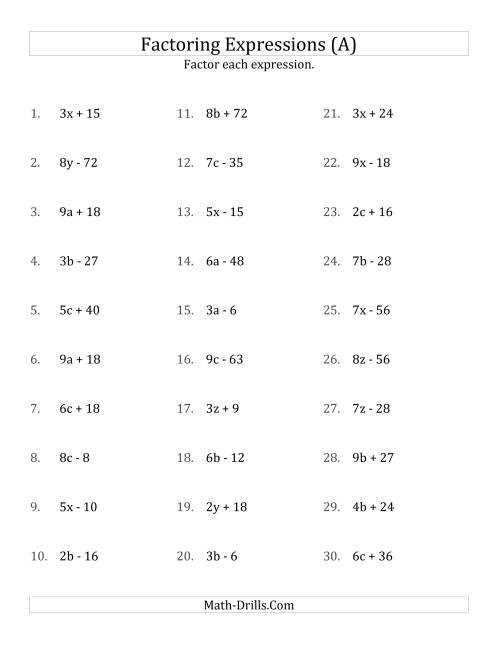
One practical application of algebraic methods is in business and finance. For instance, when calculating profit margins, determining optimal pricing, or analyzing investment returns, simplifying equations can help businesses make more informed decisions. In such scenarios, understanding how to break down expressions and solve for key variables is crucial for accurate forecasts and strategies.
- Calculating profit based on fixed and variable costs.
- Determining break-even points in sales projections.
- Optimizing production processes by analyzing resource allocation.
Understanding Engineering and Design Challenges
Another area where algebraic methods play a critical role is engineering. Engineers often need to solve problems involving forces, materials, and dimensions. By simplifying equations, engineers can determine the most efficient solutions to design challenges, whether it’s calculating load-bearing capacities or determining the best layout for materials.
- Analyzing structural integrity and material strength.
- Designing systems with efficient energy consumption.
- Determining optimal dimensions for manufacturing processes.
These real-life applications highlight how mastering algebraic techniques allows individuals to approach complex problems with confidence and precision. Whether in business, engineering, or other fields, being able to simplify expressions and analyze data effectively is a valuable skill.
Factoring Quadratics Explained
Simplifying quadratic expressions is an essential skill in algebra, allowing for easier solutions to equations and deeper understanding of mathematical relationships. The goal of simplifying quadratics is to break them down into smaller components that are easier to solve or manipulate. This process helps to reveal the roots or solutions of the equation, which are critical for further analysis.
Recognizing the Standard Quadratic Form
Quadratic expressions typically appear in the standard form: ax² + bx + c, where “a,” “b,” and “c” are constants, and “x” represents the variable. Identifying this form is the first step in simplifying the expression. Once recognized, you can apply various methods to simplify and solve the equation.
Methods for Simplifying Quadratics
There are several methods to simplify quadratic expressions, with the most common being:
- Factoring by grouping: This involves grouping terms in pairs and factoring them separately to find common factors.
- Using the quadratic formula: This method applies when direct factoring is difficult or impossible, helping to find the solutions to the quadratic equation.
- Completing the square: A technique where you manipulate the equation to create a perfect square trinomial, which can then be solved easily.
By understanding these methods and practicing their application, solving quadratic equations becomes more manageable and intuitive. With the right approach, complex quadratic expressions can be simplified effectively, revealing the solutions that lie within.
Using the FOIL Method for Factoring
The FOIL method is a popular technique for simplifying and expanding binomials in algebra. It involves multiplying two binomials together to find the product. By applying this method, you can break down complex expressions into simpler components, making it easier to solve or factor the given expression. FOIL stands for First, Outer, Inner, and Last, referring to the terms you multiply in a binomial product.
When using the FOIL method, it is important to follow a specific order to ensure all terms are multiplied correctly. Here’s a breakdown of how it works:
| Step | Action | Example |
|---|---|---|
| First | Multiply the first terms in each binomial. | (x)(x) = x² |
| Outer | Multiply the outer terms in the binomials. | (x)(-3) = -3x |
| Inner | Multiply the inner terms in the binomials. | (2)(x) = 2x |
| Last | Multiply the last terms in each binomial. | (2)(-3) = -6 |
After multiplying all terms, you combine like terms to get the final expression. For example, multiplying (x + 2)(x – 3) results in:
x² – 3x + 2x – 6 = x² – x – 6
By following the FOIL method step by step, you can expand binomial expressions and also use the process in reverse to simplify expressions by identifying patterns and breaking them down into binomial factors.
Factoring Trinomials on Day 2
Breaking down more complex polynomial expressions is an important step in mastering algebra. One of the key challenges is simplifying trinomials, which are expressions with three terms. By understanding the structure of these expressions, you can learn how to find two binomials that, when multiplied together, give you the original trinomial. This technique not only simplifies equations but also helps to solve them more efficiently.
Identifying the Key Components of a Trinomial
In order to simplify trinomials, it’s important to first recognize the key components: the coefficient of the first term, the middle term, and the constant. The goal is to identify two numbers that multiply to give the product of the first and last terms, while adding up to the middle term. This step is essential for simplifying the expression.
| Step | Action | Example |
|---|---|---|
| 1. Identify the product | Multiply the first and last terms of the trinomial. | (x²) * (3) = 3 |
| 2. Find factor pairs | Find two numbers that multiply to the product and add up to the middle term. | Numbers that multiply to 3 and add to 4 are 1 and 3. |
| 3. Break apart the middle term | Rewrite the middle term using the factor pair found. | x² + x + 3x + 3 |
| 4. Group and factor | Group the terms and factor out the common factor from each group. | (x + 1)(x + 3) |
Applying the Process to Real Examples
By applying the steps above, you can factor trinomials of various forms. For example, consider the trinomial x² + 4x + 3. Using the method described, you can break it down into two binomials: (x + 1)(x + 3). This process simplifies the expression and allows you to solve quadratic equations more easily.
Mastering trinomial simplification is a critical skill in algebra, providing the foundation for more complex problem-solving techniques. As you practice, this process will become faster and more intuitive, leading to greater mathematical confidence.
How to Check Factoring Answers
Once you’ve simplified an expression into its factors, it’s important to ensure that your work is correct. Verifying your results is a crucial step in the process, as it helps identify any errors early on. There are different methods you can use to check your work, ensuring that the simplified expression matches the original one.
Methods for Verifying the Factoring Process
There are several ways to confirm that the factored form is correct. The most common approach is to expand the factors and check if the original expression is obtained. Below are the steps for checking your work:
- Expand the Factors: Multiply the factors you obtained to see if they result in the original expression.
- Use the FOIL Method: Apply the FOIL method to the binomials and check if all terms match with the original equation.
- Check for Common Errors: Ensure that no terms were missed or incorrectly simplified during the process.
- Substitute Values: Choose a number to substitute into both the original equation and the factored form to check for consistency.
Example of Verification
Consider the expression x² + 5x + 6. Let’s check the factoring process:
- We factor the expression as (x + 2)(x + 3).
- Now, we expand (x + 2)(x + 3) using the FOIL method:
- First: x * x = x²
- Outer: x * 3 = 3x
- Inner: 2 * x = 2x
- Last: 2 * 3 = 6
- The result is x² + 5x + 6, which matches the original expression, confirming the factorization is correct.
By following these steps and using the methods above, you can easily check if your factorization is correct and avoid making mistakes in the process.
Resources for Further Practice
To build a stronger foundation in simplifying expressions and mastering algebraic techniques, it is essential to use a variety of resources. Whether you are looking for interactive exercises, practice problems, or instructional videos, there are many tools available to enhance your skills. Below are some helpful resources to continue improving your abilities.
Online Platforms for Practice

Numerous websites offer interactive exercises and step-by-step tutorials for reinforcing concepts. These platforms allow you to practice at your own pace, providing instant feedback on your work.
- Khan Academy: Offers free, comprehensive lessons on algebraic expressions and simplifications, along with practice exercises.
- IXL: Provides tailored practice questions with immediate feedback, making it easy to track progress.
- Wolfram Alpha: A computational engine that can check and explain the steps of algebraic simplifications.
Books and Study Guides
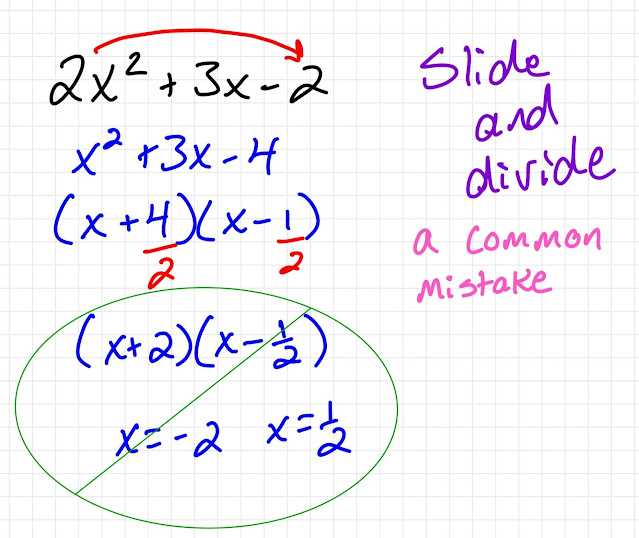
In addition to online resources, books and study guides are excellent tools for deepening your understanding. These resources often offer a more structured approach, starting from basic concepts and progressing to more advanced topics.
- “Algebra for Dummies” by Mary Jane Sterling: A user-friendly guide that explains key algebraic concepts and provides exercises for practice.
- “Algebra 1: A Common Core Curriculum” by Ron Larson: This textbook provides in-depth explanations and a wide variety of practice problems.
- Practice Problem Sets: Many math textbooks include sections of problems with answers and detailed solutions for self-checking.
Interactive Tools and Apps
Using mobile apps or software can be a great way to make learning more engaging. These tools provide a variety of interactive methods to practice and apply what you’ve learned.
- Photomath: A mobile app that allows users to take pictures of math problems and provides step-by-step solutions.
- Algebra Touch: An app designed to help users solve equations interactively, which is great for visual learners.
By using these resources, you can strengthen your algebra skills and gain more confidence in solving complex expressions. Consistent practice is key to mastering any concept, and these tools provide the perfect opportunity to do so.
Next Steps After Factoring Day 2
Once you’ve gained a solid understanding of the basic concepts and techniques for simplifying expressions, it’s important to continue building on that knowledge. Moving forward, you can explore more complex problems and refine your skills. The next steps involve tackling increasingly challenging topics, practicing a variety of problem types, and applying the techniques to real-world situations.
Expand to More Advanced Topics
After mastering the fundamentals, it’s essential to dive deeper into related concepts. This will help strengthen your overall understanding of algebra and prepare you for more complex challenges.
- Work with polynomials: Start solving problems that involve higher-degree expressions and practice breaking them down into factors.
- Explore quadratic equations: Learn how to solve and manipulate quadratic equations, which will further improve your problem-solving skills.
- Practice with word problems: Apply your knowledge to real-life scenarios where algebraic methods are needed to find solutions.
Practice Consistently with New Problems

To master any skill, regular practice is key. Set aside time each day or week to work through a variety of problems. As you progress, focus on solving problems that push your boundaries and challenge your understanding.
- Use online resources: Websites, apps, and problem-solving platforms provide endless practice opportunities that can adapt to your learning pace.
- Join study groups: Collaborating with others can expose you to different approaches and solutions, which can enhance your learning experience.
- Work with practice books: Many algebra workbooks offer targeted exercises and solutions to help reinforce concepts.
By continuing to practice and explore more advanced topics, you’ll develop a deeper understanding of mathematical techniques and become more confident in solving increasingly complex problems.