Algebra 1 Quarter 3 Exam Answers and Solutions

Preparing for an important academic assessment can be overwhelming, but with the right approach, it becomes manageable and even rewarding. This section focuses on providing the necessary tools and resources to help you excel in your upcoming evaluation. From understanding the core topics to improving problem-solving techniques, we’ll guide you through the process step by step.
With focused practice and careful review, you can confidently tackle various types of questions that may appear in your test. The goal is not only to grasp the material but also to develop a systematic approach that will lead to success. By honing your skills and understanding the underlying principles, you can significantly increase your chances of achieving a high score.
Let’s dive into the essential strategies that will aid in mastering the content and boosting your performance. Whether you’re reviewing key formulas or practicing with sample problems, the information provided will equip you with the knowledge needed to tackle the challenges ahead. Stay consistent, stay focused, and watch your confidence grow.
Algebra 1 Quarter 3 Exam Answers
In this section, we will focus on the essential topics and key techniques that will help you navigate the challenges in your upcoming test. It’s important to approach each problem systematically, using the correct formulas and methods. By practicing specific types of problems and understanding the reasoning behind each solution, you will be better prepared for any question that comes your way.
Key Topics to Focus On
- Simplifying expressions and solving equations
- Understanding linear functions and graphing techniques
- Working with inequalities and their solutions
- Manipulating exponents and powers
- Factoring polynomials and quadratic expressions
Effective Problem-Solving Strategies
- Read each question carefully to identify what is being asked.
- Write down key information and relevant formulas before solving.
- Break complex problems into smaller, more manageable steps.
- Check your work by substituting your solution back into the original equation.
- Practice regularly to increase both speed and accuracy.
By focusing on these areas, you can develop a solid understanding of the material and gain confidence in solving a wide range of problems. Make sure to review sample problems, and remember that consistent practice is key to mastering the concepts.
Understanding the Algebra 1 Exam Format
Before tackling any test, it’s essential to familiarize yourself with its structure. Knowing the layout of the assessment will allow you to manage your time better and approach each section with confidence. This section will help you understand the types of questions you may encounter and how to prepare for them effectively.
Types of Questions You Will Encounter

- Multiple choice questions – These questions test your ability to quickly recognize correct solutions from several options.
- Fill-in-the-blank questions – Here, you will need to complete expressions or equations based on your understanding of the material.
- Word problems – These require you to apply your knowledge to real-life situations, translating the text into mathematical operations.
- Graphing and interpretation – You may be asked to plot points or interpret graphs based on given information.
How the Test Is Scored
Understanding the scoring system is vital for knowing how to prioritize your time. Tests are often divided into sections with different weightings. For instance, problem-solving questions may be worth more points than multiple-choice questions. Be sure to allocate more time to the sections that carry higher value. Practice regularly and focus on areas with higher point potential.
By knowing what to expect, you can approach the assessment with a clear strategy, improving your chances of success. Understanding the format will help reduce anxiety and allow you to concentrate on solving each problem effectively.
Key Concepts to Review Before the Exam
Before sitting for any major assessment, it’s crucial to review the core principles and techniques that are most likely to appear. Focusing on these fundamental ideas will not only help reinforce your understanding but also boost your confidence. Here, we’ll outline the key areas you should revisit in preparation for the upcoming challenge.
Essential Mathematical Operations to Master
- Simplifying expressions – Be comfortable reducing complex terms and performing arithmetic operations within expressions.
- Solving equations – Practice balancing equations by isolating variables and using inverse operations.
- Working with fractions – Understand how to add, subtract, multiply, and divide fractions efficiently.
- Manipulating exponents – Review rules for multiplying and dividing powers, as well as working with negative exponents.
Graphing and Interpreting Data
- Plotting coordinates – Be familiar with graphing points on the coordinate plane and interpreting their meaning in context.
- Understanding linear functions – Know how to identify slopes, y-intercepts, and graphing lines based on given equations.
- Reading charts and graphs – Practice interpreting data from visual representations, including bar graphs and line charts.
Revisiting these topics will not only ensure you are well-prepared but also improve your problem-solving speed. Make sure to practice various problem types to gain familiarity with the expected format. With targeted review and consistent practice, you’ll approach the test with greater ease and precision.
How to Solve Algebraic Expressions
Solving mathematical expressions involves applying a series of steps to simplify or evaluate them correctly. It’s essential to understand the rules of operation and how to manipulate variables and constants to find the solution. By following a logical approach and practicing different types of expressions, you can develop a strong understanding of how to solve them effectively.
Start by identifying the terms in the expression. These may include variables, constants, and mathematical operations such as addition, subtraction, multiplication, or division. The next step is to simplify the expression by combining like terms or applying the distributive property if necessary. Always remember to perform operations in the correct order, following the rules of parentheses, exponents, multiplication/division, and addition/subtraction (PEMDAS).
For more complex expressions, consider breaking the problem into smaller, more manageable parts. This will help you avoid mistakes and ensure accuracy in your calculations. It’s crucial to stay organized and methodical when approaching each problem. Consistent practice with different types of expressions will help build confidence and mastery over time.
Common Mistakes in Algebra 1 Exams

During any mathematical test, it’s easy to make small errors that can lead to incorrect results. These mistakes can often be traced back to misunderstandings of key concepts or simple oversights. By being aware of these common pitfalls, you can take steps to avoid them and improve your performance.
Frequent Errors to Watch Out For
- Misapplying the order of operations – Failing to follow the correct sequence when simplifying expressions can lead to mistakes in the final solution.
- Forgetting to distribute – When working with parentheses, it’s essential to apply the distributive property correctly. Missing this step can lead to wrong answers.
- Sign errors – Incorrectly handling positive and negative signs, especially when multiplying or dividing, is a common mistake.
- Overlooking like terms – When simplifying expressions, be sure to combine only like terms. Neglecting this can cause errors in your calculations.
- Not checking solutions – Always substitute your answer back into the original problem to verify its correctness. Many students skip this step, missing simple mistakes.
How to Avoid These Mistakes

- Review the order of operations – Practice solving problems using PEMDAS (parentheses, exponents, multiplication/division, addition/subtraction) to strengthen your understanding.
- Double-check signs and calculations – Take an extra moment to ensure that you’ve handled signs properly, particularly when working with negative numbers.
- Take your time with distribution – Carefully distribute terms across parentheses to ensure accuracy when simplifying.
- Review and verify your answers – After solving a problem, always check your work by plugging your solution back into the original equation.
By staying mindful of these common errors, you can greatly improve your accuracy and avoid unnecessary mistakes during your assessment. Consistent practice and attention to detail are key to mastering the material.
Effective Study Tips for Algebra 1
Studying for a math test can often feel overwhelming, but with the right strategies, you can improve both your understanding and retention of the material. Adopting effective study habits not only helps you grasp the key concepts but also boosts your confidence when facing a challenge. Here are some helpful tips to make your study sessions more productive and focused.
Study Strategies to Improve Understanding
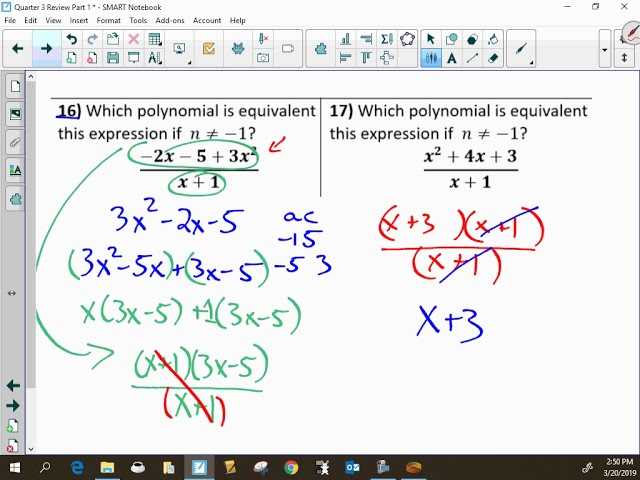
- Practice consistently – Repetition is key to mastering any mathematical concept. Solve different types of problems regularly to build familiarity and fluency.
- Break down complex problems – Don’t try to solve complicated problems all at once. Break them into smaller, manageable steps to make them easier to approach.
- Focus on weak areas – Identify the concepts or problem types that you struggle with the most and dedicate extra time to reviewing them.
- Use visual aids – Diagrams, charts, and graphs can help clarify complex concepts and make abstract ideas easier to understand.
Maximize Your Study Sessions
- Create a study schedule – Plan your study time in advance and stick to it. Spacing out your study sessions over time will help reinforce what you’ve learned.
- Study actively – Instead of just reading notes or examples, actively work through problems and explain concepts to yourself or others.
- Take regular breaks – Studying for long periods without breaks can lead to burnout. Take short breaks to refresh your mind and maintain focus.
- Review mistakes – After solving practice problems, review any mistakes you made. Understanding why you got a problem wrong is crucial for learning.
By following these strategies, you can approach your studies in a more organized and efficient way. Consistent practice and a focused mindset will lead to better comprehension and improved performance in any assessment.
Step-by-Step Guide to Answering Questions

Approaching problems methodically can make a huge difference when solving mathematical questions. Having a clear, step-by-step approach helps ensure accuracy and minimizes the risk of making simple mistakes. By following a structured process, you can tackle even the most challenging problems with confidence.
Breaking Down the Problem
- Read the question carefully – Take your time to understand what the question is asking. Identify key information such as variables, operations, and what needs to be solved.
- Identify the operations – Determine which mathematical operations (addition, subtraction, multiplication, etc.) are required to solve the problem.
- Organize the work – Write out the equation or expression clearly, making sure all steps are visible. This will help keep your work organized and prevent skipping steps.
Executing the Solution
- Perform calculations carefully – Follow the order of operations, ensuring each step is completed correctly before moving on to the next.
- Check for common errors – Double-check signs, arithmetic operations, and the order of operations to avoid simple mistakes that could lead to incorrect answers.
- Verify the solution – Once you reach a solution, substitute your answer back into the original problem to verify its correctness.
By taking the time to follow these steps, you can approach each question with a clear plan and minimize the chances of error. Consistent practice with this structured method will help you become more efficient and accurate in solving problems.
Tips for Time Management During the Test

Efficient time management is essential when working under pressure. During a math test, it’s easy to get stuck on difficult questions or rush through easier ones. By organizing your time wisely, you can maximize your performance and ensure that you have enough time to tackle every question.
One of the best ways to manage your time is to prioritize questions based on their difficulty and the points they carry. This will allow you to focus on questions that may take more time while ensuring you don’t miss out on easier, faster ones. Here are a few strategies that can help you stay on track:
| Time Management Tips | Strategy |
|---|---|
| Read through the entire test first | Get an overview of all the questions to understand which ones are more time-consuming and which ones can be answered quickly. |
| Allocate time for each section | Set a specific amount of time for each section or question. For example, spend 5 minutes on short-answer questions and 10 minutes on long problems. |
| Start with easy questions | Answer the questions you know best first. This builds confidence and ensures you get those points quickly. |
| Move on if stuck | If a question is taking too long, move on to the next one. Come back to it later if time allows. |
| Keep track of time | Check the clock regularly to ensure you’re on pace. If necessary, adjust your pace to stay on track. |
By following these strategies, you can avoid unnecessary stress and make the most of your test time. Practicing these techniques beforehand will help you approach the test with confidence and ensure a more efficient use of your time.
How to Check Your Answers Efficiently

Reviewing your work thoroughly before submitting it is essential to avoid careless mistakes. A systematic approach to checking your solutions can help ensure accuracy and give you the confidence that you’ve completed each task correctly. By following a structured review process, you can identify any errors or missed steps in your calculations.
Here are some key strategies to check your solutions efficiently:
| Review Strategy | How It Helps |
|---|---|
| Double-check calculations | Go over your math steps to confirm that no arithmetic mistakes were made. Recalculate key parts to ensure consistency. |
| Verify units and labels | Make sure that any units of measurement are correct, and that you’ve properly labeled your variables and solutions. |
| Revisit the problem statement | Ensure that you answered the question that was actually asked. Sometimes, it’s easy to misinterpret the problem. |
| Check for common mistakes | Look for frequent errors such as sign mistakes, order of operations errors, or overlooking negative signs. |
| Work backward when possible | If applicable, plug your solution back into the original problem to check if it satisfies the equation or condition. |
By following these steps, you can efficiently review your work and catch any mistakes before submitting it. Regular practice with this review process will help you become more thorough and reduce the likelihood of errors in future tasks.
Sample Problems and Solutions for Practice
Practicing with sample problems is one of the best ways to strengthen your understanding and boost your confidence. By solving a variety of problems, you can become familiar with different types of questions and develop effective strategies for approaching them. Below are some sample problems, along with their solutions, to help you refine your skills.
Working through these examples will allow you to see the step-by-step process involved in solving typical questions, giving you a clearer idea of how to apply concepts and techniques effectively.
Sample Problem 1: Simplifying Expressions
Problem: Simplify the expression: 3x + 4x – 5 + 2x
Solution:
- First, combine like terms: 3x + 4x + 2x = 9x
- Then, write the simplified expression: 9x – 5
The simplified expression is 9x – 5.
Sample Problem 2: Solving Equations
Problem: Solve for x: 2x + 5 = 15
Solution:
- First, subtract 5 from both sides: 2x = 10
- Next, divide both sides by 2: x = 5
The solution is x = 5.
Sample Problem 3: Word Problem
Problem: A rectangle’s length is 3 times its width. If the perimeter is 32 units, find the length and width.
Solution:
- Let the width be w. Then, the length is 3w.
- Perimeter of a rectangle is 2(length + width), so: 2(3w + w) = 32.
- Simplify the equation: 2(4w) = 32, which gives 8w = 32.
- Now, divide by 8: w = 4.
- The length is 3w = 3(4) = 12.
Therefore, the width is 4 units and the length is 12 units.
By practicing these types of problems, you can become more comfortable with problem-solving techniques and better prepared for upcoming challenges.
Understanding Word Problems in Algebra
Word problems can often seem intimidating at first, as they require translating real-world scenarios into mathematical expressions. However, once you develop a systematic approach, solving these problems becomes much more manageable. The key is to carefully analyze the problem, identify the relevant information, and set up the appropriate equation to find the solution.
Here’s a step-by-step method for approaching word problems:
- Read the problem carefully: Make sure you understand the context and what is being asked. Look for key terms that indicate mathematical operations.
- Identify the unknowns: Determine what the problem is asking you to find. This is typically represented by a variable such as x.
- Translate the words into an equation: Convert the information from the problem into an algebraic equation by recognizing patterns and relationships between quantities.
- Solve the equation: Once you have the equation set up, apply the appropriate mathematical techniques to solve for the unknown.
- Check your solution: After solving, check if the solution makes sense in the context of the problem.
Let’s look at a typical word problem example:
Example Problem:
Problem: Sarah has three times as many apples as Tom. Together, they have 40 apples. How many apples does each person have?
Solution:
- Let the number of apples Tom has be x.
- Then, the number of apples Sarah has is 3x.
- The total number of apples is given as 40, so: x + 3x = 40.
- Simplifying the equation: 4x = 40.
- Dividing both sides by 4: x = 10.
- So, Tom has 10 apples, and Sarah has 3(10) = 30 apples.
By following this method, you can approach any word problem with confidence. Practice will help you recognize patterns and make the process quicker and more intuitive.
Important Formulas to Memorize for the Exam
Understanding and memorizing key mathematical formulas is essential for solving a wide variety of problems efficiently. These formulas serve as tools that can simplify complex calculations and help you quickly identify relationships between variables. Mastering these formulas will not only save time but also ensure accuracy in your problem-solving approach.
Here are some important formulas that you should be familiar with:
- Linear Equation: y = mx + b, where m is the slope and b is the y-intercept. This formula represents the equation of a straight line.
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a, used to find the solutions to a quadratic equation of the form ax² + bx + c = 0.
- Pythagorean Theorem: a² + b² = c², where a and b are the legs of a right triangle, and c is the hypotenuse.
- Slope Formula: m = (y₂ – y₁) / (x₂ – x₁), used to calculate the slope between two points (x₁, y₁) and (x₂, y₂).
- Distance Formula: d = √((x₂ – x₁)² + (y₂ – y₁)²), used to find the distance between two points in a coordinate plane.
- Area of a Triangle: A = 1/2 * base * height, used to calculate the area of a triangle.
- Area of a Circle: A = πr², used to calculate the area of a circle, where r is the radius.
- Circumference of a Circle: C = 2πr, used to calculate the circumference of a circle.
Familiarity with these formulas allows you to quickly recognize the problem type and apply the correct formula to reach the solution. Practice using these formulas in different scenarios to ensure that you are prepared to tackle a wide range of mathematical questions.
How to Handle Tough Algebra Questions
When faced with challenging mathematical problems, it’s easy to feel overwhelmed. However, breaking down the problem step by step and applying a logical approach can make even the toughest questions more manageable. With the right strategies, you can approach these problems with confidence and precision.
Step 1: Read the Problem Carefully

The first step in tackling any difficult question is to carefully read the entire problem. Pay attention to all the details and make sure you understand what is being asked. Often, the key to solving the problem lies in identifying the important information and recognizing the relevant relationships between variables.
Step 2: Break the Problem Into Parts
Large or complicated problems can often be broken down into smaller, more manageable steps. Identify the sub-problems within the main question and solve each one separately. This will help you maintain focus and avoid feeling overwhelmed.
- Identify known and unknown values: Clearly define what is given and what needs to be found.
- Set up equations: Translate the problem into mathematical expressions that represent the relationships between the variables.
- Work through one step at a time: Solve each part systematically, and double-check your work as you go.
Step 3: Use a Methodical Approach

Apply the appropriate mathematical techniques or formulas to solve the problem. Whether you’re working with linear equations, systems of equations, or geometric principles, using a step-by-step approach ensures that you don’t overlook important steps. It’s also a good idea to check your progress at each stage to ensure you’re on the right track.
For more complex problems, consider looking for patterns or using strategies such as substitution or elimination to simplify the process. Remember, persistence is key, and with enough practice, tackling difficult questions becomes much easier.
Utilizing Online Resources for Math Help

In today’s digital age, there are countless online tools and resources that can assist you in mastering mathematical concepts. Whether you’re looking for detailed explanations, practice problems, or step-by-step solutions, the internet offers a wide range of options to help enhance your understanding and improve problem-solving skills. With the right online resources, tackling difficult problems can become a much more manageable and even enjoyable task.
Key Online Resources for Math Help
| Resource | Features | Best For |
|---|---|---|
| Online Tutorials | Interactive lessons, video explanations, step-by-step guides | Understanding concepts and learning new techniques |
| Practice Problem Solvers | Instant solutions, practice problems, detailed explanations | Improving problem-solving speed and accuracy |
| Math Forums and Communities | Ask questions, get help from experts, collaborate with peers | Clarifying doubts and engaging in discussions |
| Educational Apps | Interactive problem sets, quizzes, personalized feedback | Quick practice and reinforcing knowledge |
These online resources provide a great way to study and reinforce important concepts. Many of them are free or offer affordable access to high-quality materials, making them an excellent option for both self-study and guided learning.
How to Make the Most of Online Resources

While using online resources, it’s important to approach them with a structured plan. Set specific learning goals, such as mastering a particular topic or solving a set number of practice problems, and use the tools to track your progress. Additionally, make sure to review any solutions or explanations carefully to ensure you fully understand the logic behind the steps taken.
By integrating these digital tools into your study routine, you can effectively build your confidence, improve your skills, and achieve greater success in mathematics.
What to Expect on Quarter 3 Exam
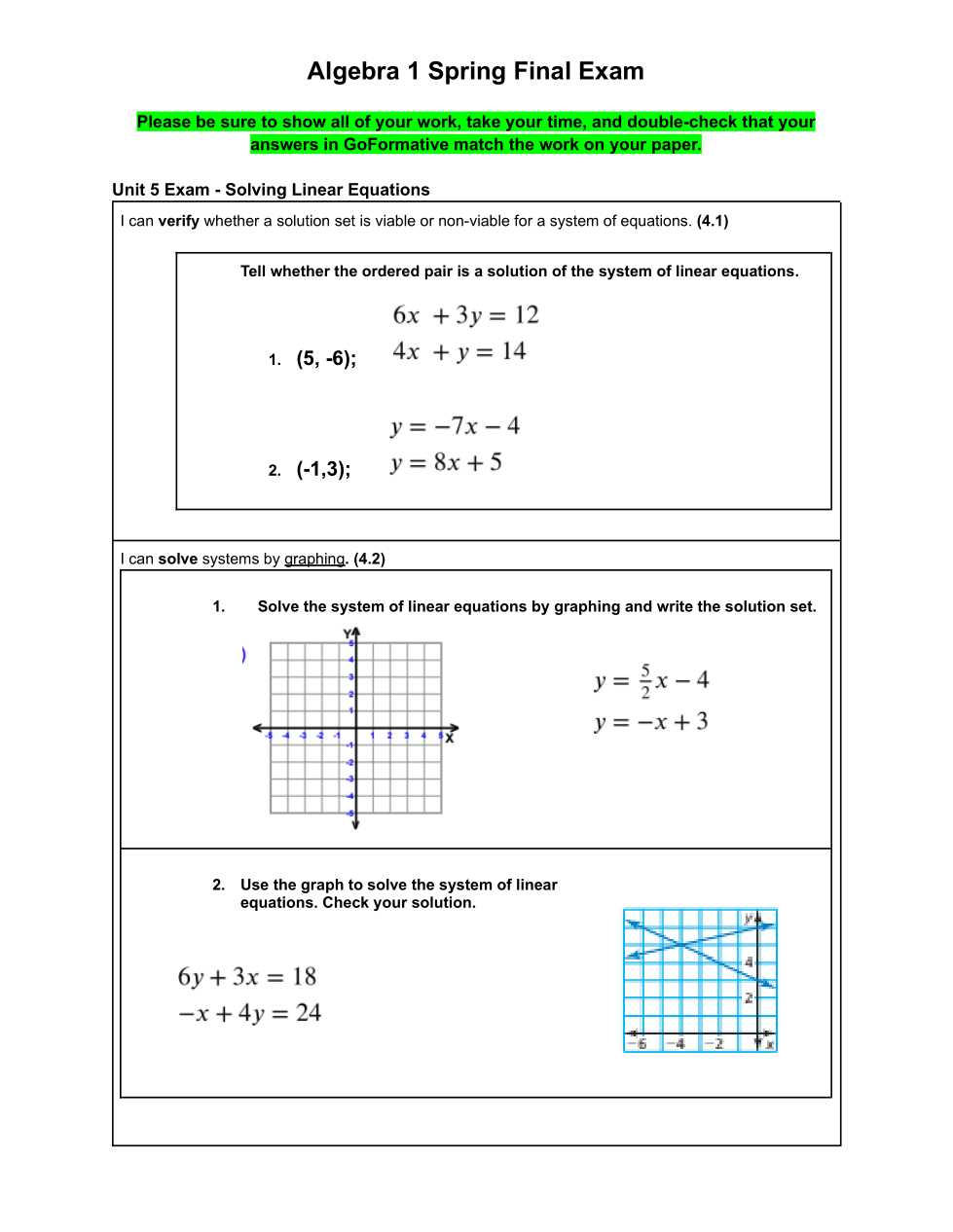
As you prepare for the upcoming assessment, it’s important to understand the key areas that will be tested. This period focuses on building upon the concepts you’ve learned so far and applying them to more complex problems. The test will challenge your ability to solve problems efficiently, demonstrating a deep understanding of the material. Here’s what you can expect:
Core Topics Covered
- Equations and Inequalities – You will be asked to solve both linear and quadratic equations, as well as interpret and solve inequalities.
- Functions – Expect questions on analyzing and interpreting functions, including finding domain, range, and graphing various types of functions.
- Systems of Equations – You’ll need to solve systems of linear equations using substitution, elimination, or graphing techniques.
- Word Problems – Problem-solving skills will be essential, with word problems that involve setting up and solving equations based on real-life scenarios.
- Graphing – Understanding how to graph different types of functions and equations, as well as interpreting graphs, will be key.
Question Types
- Multiple Choice – Some questions may present you with several possible answers, requiring you to select the correct one.
- Short Answer – You’ll be asked to solve problems and provide a clear, written solution.
- Show Your Work – For certain problems, you will need to show each step of your solution process, which will demonstrate your understanding of the method.
- Word Problems – Be prepared for questions that involve interpreting real-world situations and translating them into mathematical equations.
Make sure to review the material thoroughly and practice solving problems in each of these areas. Familiarity with the question types and topics will help you approach the test with confidence and improve your chances of success.
Strategies for Staying Calm During the Test
Tests can often be a source of stress, but managing anxiety effectively is key to performing well. Staying calm allows you to focus, think clearly, and solve problems more efficiently. There are several strategies you can use before and during the test to help you remain composed and confident.
Before the Test
- Prepare Thoroughly: The more prepared you are, the less anxious you’ll feel. Spend time reviewing key concepts and practicing problems ahead of time.
- Get Enough Rest: A good night’s sleep before the test ensures that your mind is sharp and focused. Avoid staying up late cramming.
- Eat Well: A balanced meal before the test helps to maintain energy levels and prevents distractions caused by hunger.
- Stay Positive: Cultivate a positive mindset. Believe in your abilities and remind yourself that you’ve put in the work to succeed.
During the Test
- Take Deep Breaths: If you start feeling overwhelmed, pause for a moment, close your eyes, and take several deep breaths to calm your nerves.
- Read Questions Carefully: Make sure to carefully read and understand each question before answering. This will help you avoid unnecessary mistakes caused by rushing.
- Manage Your Time: Keep track of time, but don’t obsess over it. Allocate time for each section and move on if you’re stuck, coming back to difficult questions later.
- Stay Focused: Block out distractions, whether it’s other test-takers or external noises. Focus only on the task at hand and take it one question at a time.
By implementing these strategies, you’ll be able to maintain a calm and focused mindset, helping you tackle the test with confidence and perform at your best.
How to Review Your Mistakes After the Test
Once you’ve completed a test, it’s essential to reflect on your performance, particularly the areas where you made mistakes. Reviewing errors allows you to identify patterns in your thinking, understand where you went wrong, and improve for future assessments. This process not only helps you learn from your mistakes but also enhances your overall problem-solving skills.
Identify the Mistakes
- Go Through Each Question: Start by reviewing each question you answered incorrectly. Try to understand why you made that mistake and whether it was due to a simple oversight or a misunderstanding of the concept.
- Check for Careless Errors: Often, small mistakes occur due to rushing or not double-checking your work. Take note of these mistakes and make sure to slow down in the future.
- Analyze Misunderstood Concepts: If a mistake was due to a lack of understanding, identify the concept that caused confusion. This may require reviewing relevant materials or seeking clarification from a teacher.
Learn and Improve
- Correct the Errors: After identifying the mistakes, correct them. Rework the problems and make sure you fully understand the steps involved in solving them.
- Practice Similar Problems: To reinforce your understanding, practice similar problems to ensure that you don’t make the same mistakes again. Consistent practice will help you solidify your grasp of the concepts.
- Ask for Feedback: If you’re still unsure about certain mistakes, don’t hesitate to ask your teacher for feedback. They can provide valuable insights into where you went wrong and guide you in the right direction.
Reviewing your mistakes is an important step in learning and improving. By focusing on your errors, understanding the root causes, and actively practicing to correct them, you’ll be better prepared for future challenges.