Algebra One Final Exam Questions and Answers

Preparation for a comprehensive mathematics test requires a solid understanding of key concepts and problem-solving techniques. Whether you’re reviewing equations, functions, or other critical areas, it’s essential to approach your studies systematically and confidently. A structured plan and plenty of practice are the keys to success.
Throughout this guide, you’ll find a range of exercises designed to reinforce your knowledge and boost your problem-solving skills. By practicing various types of problems, you will improve your ability to tackle even the most challenging questions effectively. Key strategies and helpful insights are also provided to enhance your study experience and ensure thorough preparation.
Mathematics Assessment Study Guide
Successfully preparing for a comprehensive mathematics test involves mastering a variety of essential concepts and techniques. To ensure a strong performance, it’s important to break down each topic into manageable sections and focus on both understanding the principles and refining your problem-solving abilities.
This study guide will help you navigate through key areas such as solving equations, working with functions, graphing, and more. By dedicating time to each of these topics, you’ll be equipped to confidently approach a range of problems. Regular practice, alongside strategic review of key formulas and methods, will solidify your readiness.
Key Concepts to Master for Mathematics

To perform well on a mathematics assessment, it’s essential to understand a variety of fundamental concepts that form the backbone of problem-solving. Focusing on these critical areas will ensure that you are well-prepared for different types of questions that might appear on the test. Each topic contributes to a broader understanding of the subject, making it easier to approach more complex problems.
Equations and Functions
Mastering the rules of solving different types of equations is crucial. This includes both linear and quadratic equations, as well as understanding how to manipulate and simplify expressions. Functions are equally important, as they form the basis for many mathematical problems.
Graphing and Geometry
Understanding how to graph equations and interpret graphs is another key area. This involves knowledge of plotting points, analyzing slopes, and recognizing the characteristics of different types of graphs. Geometry skills, such as calculating areas, perimeters, and understanding shapes, are also essential.
| Concept | Description |
|---|---|
| Equations | Solving linear and quadratic equations through different methods. |
| Functions | Understanding function notation and solving function-related problems. |
| Graphing | Plotting equations and analyzing the relationships between variables. |
| Geometry | Working with shapes, calculating areas, perimeters, and volumes. |
Top Mathematics Test Tips
Approaching a comprehensive mathematics assessment requires careful preparation and effective strategies to tackle a wide variety of problems. By applying specific techniques, you can improve your efficiency and confidence, ensuring you’re ready to face the test head-on. These tips are designed to help you maximize your performance and avoid common pitfalls.
One of the most effective strategies is time management. Practice solving problems under timed conditions to develop a sense of pacing. This ensures you can complete all sections within the given time frame. Additionally, understanding the types of questions that are likely to appear can help you focus on the most important areas during your review.
Another important tip is to always double-check your work. In the midst of solving problems, it’s easy to overlook simple mistakes, so take a moment to review your answers before moving on to the next question. This can often make the difference between a correct and incorrect solution.
Understanding Mathematical Expressions Clearly
Grasping the structure and meaning of mathematical expressions is a crucial skill for solving problems efficiently. These expressions often combine variables, constants, and operations, and understanding how each part interacts is essential. Breaking down these elements helps to simplify complex problems and enhances your ability to solve them step by step.
Components of a Mathematical Expression
A mathematical expression typically consists of variables, coefficients, and operators. The variables represent unknown values, while coefficients are numerical values that multiply the variables. Operators like addition, subtraction, multiplication, and division indicate how these components interact. Recognizing how to manipulate these elements will help you solve a wide range of problems.
Simplifying Expressions
To simplify an expression, it’s important to combine like terms and apply the correct order of operations. This reduces the expression to its simplest form, making it easier to understand and solve. Familiarity with these techniques ensures that you can approach any problem with confidence.
How to Solve Linear Equations
Solving linear equations involves finding the value of the unknown variable that satisfies the equation. These equations are often simple but require a clear approach to ensure accuracy. The goal is to isolate the variable on one side of the equation through a series of logical steps.
Follow these basic steps to solve linear equations:
- Identify the variable: Determine which symbol represents the unknown quantity.
- Simplify both sides: Combine like terms and remove parentheses if needed.
- Isolate the variable: Use inverse operations (addition, subtraction, multiplication, or division) to move terms around and isolate the variable.
- Check your solution: Substitute the value you found back into the original equation to verify the result.
Here’s an example:
- Equation: 3x + 5 = 11
- Step 1: Subtract 5 from both sides: 3x = 6
- Step 2: Divide both sides by 3: x = 2
By following these steps, you’ll be able to solve linear equations efficiently and accurately every time.
Factoring Techniques for Mathematics Assessments
Factoring is an essential skill in mathematics, allowing you to break down expressions into simpler components. Mastering factoring techniques can help you solve complex problems more efficiently, especially when dealing with quadratic and higher-order polynomials. By recognizing patterns and applying the right methods, you can simplify expressions and find solutions faster.
There are several key factoring techniques that every student should master:
- Factoring by Grouping: This method involves grouping terms in pairs and factoring out the greatest common factor (GCF) from each pair.
- Factoring Quadratics: Quadratic expressions can often be factored into two binomials. Look for two numbers that multiply to the constant term and add up to the coefficient of the middle term.
- Difference of Squares: This technique applies when an expression takes the form of a^2 – b^2, which factors into (a – b)(a + b).
- Factoring Trinomials: For trinomials of the form x^2 + bx + c, find two numbers that multiply to c and add to b, and then split the middle term.
With these techniques, you can approach a variety of problems more confidently and efficiently, making factoring a valuable tool in your problem-solving arsenal.
Strategies for Quadratic Equations
Quadratic equations often appear in various mathematical assessments and require specific techniques to solve. These equations can typically be solved using multiple methods, each suited for different types of problems. Mastering these approaches will help you tackle any quadratic equation effectively, whether it’s in standard, factored, or vertex form.
Factoring Method
One of the most straightforward methods for solving quadratic equations is factoring. First, look for two numbers that multiply to the constant term and add to the coefficient of the linear term. Once you identify these numbers, split the middle term and factor the expression into two binomials. This method works best when the equation can be easily factored into integers.
Quadratic Formula
When factoring is difficult or not possible, the quadratic formula offers a reliable solution. The formula is expressed as:
x = (-b ± √(b² – 4ac)) / 2a
This formula applies to any quadratic equation in the form ax² + bx + c = 0. Simply plug in the values for a, b, and c, and solve for x. The quadratic formula is especially useful when the equation doesn’t factor neatly.
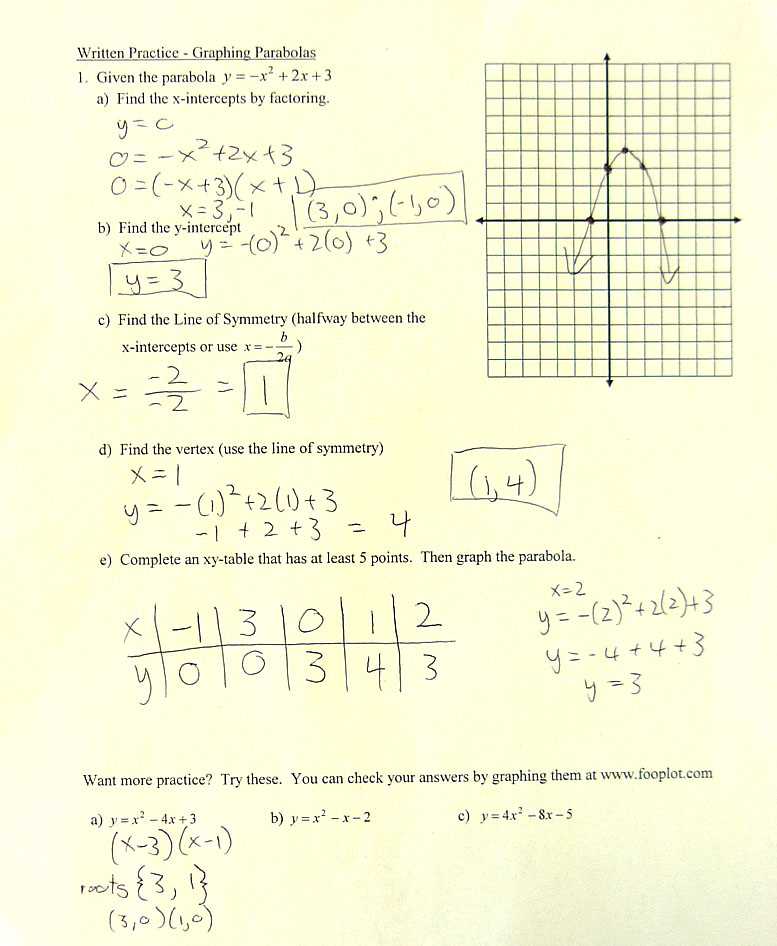
Mastering Graphing and Coordinate Geometry
Understanding how to graph functions and interpret geometric shapes on the coordinate plane is a fundamental skill in mathematics. This knowledge allows you to visualize relationships between variables and provides a powerful tool for solving problems. Whether you’re working with lines, curves, or geometric figures, mastering graphing and coordinate geometry will enhance your problem-solving abilities.
Here are key strategies to effectively graph equations and interpret geometric concepts:
- Plotting Points: Begin by identifying the coordinates (x, y) and plotting them on the grid. Make sure to accurately place each point according to the axis values.
- Understanding the Slope: The slope of a line represents its steepness and direction. You can calculate the slope by determining the ratio of vertical change to horizontal change between two points.
- Identifying Intercepts: The x-intercept is the point where the graph crosses the x-axis, while the y-intercept is where it crosses the y-axis. Knowing how to find these intercepts is crucial for graphing linear equations.
- Graphing Quadratics: For quadratic functions, plot key points such as the vertex and axis of symmetry. Understanding the shape of the graph (a parabola) will help you plot and interpret the function correctly.
By mastering these techniques, you’ll be able to confidently graph various types of equations and solve geometric problems with ease.
Common Mathematical Mistakes to Avoid
When solving mathematical problems, it’s easy to make mistakes that can lead to incorrect answers and confusion. These errors often occur due to a misunderstanding of key concepts or rushing through calculations. Being aware of common pitfalls can help you avoid them and ensure that your solutions are accurate and efficient.
Here are some frequent mistakes to watch out for:
- Misunderstanding Operations: Mixing up the order of operations or incorrectly applying addition, subtraction, multiplication, and division can lead to errors. Always follow the proper sequence: parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right).
- Forgetting to Distribute: When expanding expressions, it’s easy to forget to distribute a factor across terms. This is especially important when working with binomials. Make sure to multiply each term carefully.
- Incorrectly Solving for Variables: When isolating a variable, it’s essential to perform the same operation on both sides of the equation. Failing to do so can result in incorrect values for the variable.
- Overlooking Sign Errors: Be cautious when working with negative numbers, especially when dealing with exponents or during addition and subtraction. Sign mistakes are a common source of incorrect answers.
- Skipping Steps: Rushing through calculations or skipping intermediate steps can lead to small errors that compound as the problem progresses. Always show all your work to catch mistakes early.
By staying mindful of these common mistakes, you can approach mathematical problems more carefully and accurately, leading to better results.
Essential Mathematical Formulas You Should Know
Having a solid grasp of key mathematical formulas is crucial for solving a wide range of problems. These formulas serve as the foundation for many calculations, and knowing them well can help you approach various problems more efficiently. Whether you’re solving equations, working with functions, or analyzing geometric figures, these formulas will be invaluable tools in your mathematical toolkit.
Here are some essential formulas that every student should familiarize themselves with:
- Quadratic Formula: Used to solve quadratic equations, the formula is:
- Slope Formula: To find the slope of a line between two points (x₁, y₁) and (x₂, y₂), use:
- Slope-Intercept Form of a Line: This formula expresses the equation of a line as:
- Point-Slope Form: Another way to represent a linear equation is:
- Distance Formula: To find the distance between two points (x₁, y₁) and (x₂, y₂), use:
- Area of a Triangle: The area of a triangle can be calculated as:
x = (-b ± √(b² – 4ac)) / 2a
m = (y₂ – y₁) / (x₂ – x₁)
y = mx + b
Where “m” is the slope and “b” is the y-intercept.
y – y₁ = m(x – x₁)
d = √((x₂ – x₁)² + (y₂ – y₁)²)
A = 1/2 * base * height
By memorizing these essential formulas and practicing their application, you’ll be well-equipped to solve a variety of mathematical problems with confidence.
Time Management for Your Final Assessment
Effective time management is crucial when preparing for any significant test. It allows you to approach each task systematically, ensuring that you can review all necessary material without feeling rushed. By organizing your study sessions and allocating enough time for each section, you can maximize your performance and reduce stress on the day of the test.
Here are some key strategies to help you manage your time efficiently:
- Create a Study Schedule: Break down your study sessions into manageable blocks of time. Assign specific topics to each session, ensuring you cover all areas of the subject. Stick to the schedule to avoid last-minute cramming.
- Prioritize Tasks: Identify the areas where you feel less confident and allocate more time to them. Focus on practicing the most challenging topics first before moving on to easier ones.
- Take Regular Breaks: Avoid studying for hours without breaks. Taking short breaks between sessions can improve focus and help retain information better. A typical method is the Pomodoro Technique: 25 minutes of study followed by a 5-minute break.
- Practice Under Time Constraints: Simulate test conditions by practicing problems within a set time limit. This will help you get used to the time pressure and increase your speed in solving questions.
- Review Strategically: In the final days before the assessment, focus on reviewing key concepts and solving practice problems. Prioritize topics that carry the most weight on the test.
By managing your time wisely and staying organized, you can approach your test with confidence and increase your chances of success.
Practice Problems for Your Assessment
Practicing problem-solving is one of the most effective ways to prepare for any test. By working through different types of problems, you familiarize yourself with the format and develop strategies for approaching various questions. Regular practice builds confidence, sharpens your skills, and helps you identify areas that need more attention.
Below are a few sample problems designed to help you reinforce your knowledge and test your understanding:
Problem Set 1: Linear Equations
- Solve for x: 3x + 5 = 20
- Solve for y: 2y – 4 = 10
- Solve for x: 4(x – 2) = 16
Problem Set 2: Systems of Equations
- Solve the system:
- 3x + 2y = 12
- 4x – y = 9
- Solve the system:
- 2x + y = 10
- 3x – y = 5
Working through these problems will help you master essential skills and build your problem-solving abilities. Make sure to check your solutions and understand the steps involved in each solution process to strengthen your grasp on the material.
Understanding Exponents and Powers
Exponents and powers are fundamental concepts in mathematics, playing a key role in simplifying complex expressions and solving equations. These mathematical tools help express repeated multiplication in a compact form, making calculations more efficient. Mastering exponents is essential for progressing in many areas of math, especially when working with large numbers or dealing with polynomial expressions.
Here is a breakdown of the key concepts you need to understand:
What is an Exponent?
An exponent is a number that indicates how many times to multiply the base number by itself. For example, in the expression 23, 2 is the base and 3 is the exponent, meaning 2 should be multiplied by itself three times (2 × 2 × 2 = 8).
Basic Rules of Exponents
| Rule | Example | Result |
|---|---|---|
| Multiplying Powers with the Same Base | am × an | am+n |
| Dividing Powers with the Same Base | am ÷ an | am-n |
| Power of a Power | (am)n | am×n |
| Zero Exponent | a0 | 1 |
By following these basic rules, you can simplify expressions and solve problems involving exponents more effectively. Understanding these principles is essential when working with more complex problems, especially in polynomial equations or when dealing with large numbers in scientific contexts.
Word Problems in Algebra One Exams
Word problems often present real-world situations that require mathematical reasoning to solve. These types of questions test your ability to translate verbal descriptions into mathematical equations, which can then be solved using the appropriate methods. While word problems can seem challenging at first, breaking them down into smaller steps can make them more manageable.
To solve word problems effectively, follow these essential steps:
- Read the problem carefully: Make sure you understand all the details. Pay attention to key information such as numbers, relationships, and what the problem is asking for.
- Identify the variables: Determine what unknowns the problem is asking you to find, and assign variables (e.g., x, y) to represent these unknowns.
- Set up an equation: Use the relationships described in the problem to form a mathematical equation. This could involve addition, subtraction, multiplication, or division, depending on the situation.
- Solve the equation: Apply the appropriate methods to solve the equation and find the value of the unknowns.
- Check your solution: Always double-check your work by substituting the solution back into the original problem to see if it makes sense.
By practicing word problems regularly, you can improve your problem-solving skills and build confidence in handling different types of questions. These problems are an essential part of mathematical learning, helping you connect abstract concepts to practical applications.
Reviewing Systems of Equations
Systems of equations involve solving multiple equations simultaneously to find a common solution for all variables. These systems are fundamental in mathematics because they allow you to model and solve problems that involve more than one relationship at a time. Mastering the methods to solve these systems is crucial for tackling more complex scenarios.
There are several ways to solve systems of equations, each with its own set of advantages. Understanding the different techniques can help you choose the most effective method for each problem.
Methods for Solving Systems of Equations
- Graphing Method: This involves plotting each equation on a coordinate plane and identifying the point where the graphs intersect. This method is useful for visual learners but can be less precise if the intersection is not on a grid point.
- Substitution Method: In this approach, you solve one equation for one variable and substitute that expression into the other equation. This can simplify the system and make it easier to solve.
- Elimination Method: Here, you add or subtract equations to eliminate one variable, allowing you to solve for the remaining variable. This method is particularly useful when the coefficients of one variable are the same or can be easily manipulated.
Tips for Success
- Be Organized: When working with multiple equations, write each equation clearly and keep track of the steps you take to solve them.
- Check Your Solution: After finding a solution, substitute the values back into the original equations to ensure they satisfy all conditions.
- Practice Regularly: The more you practice solving systems of equations, the more familiar and confident you will become with the methods and steps involved.
By mastering these strategies, you can solve systems of equations efficiently and confidently, making it easier to approach more advanced mathematical problems.
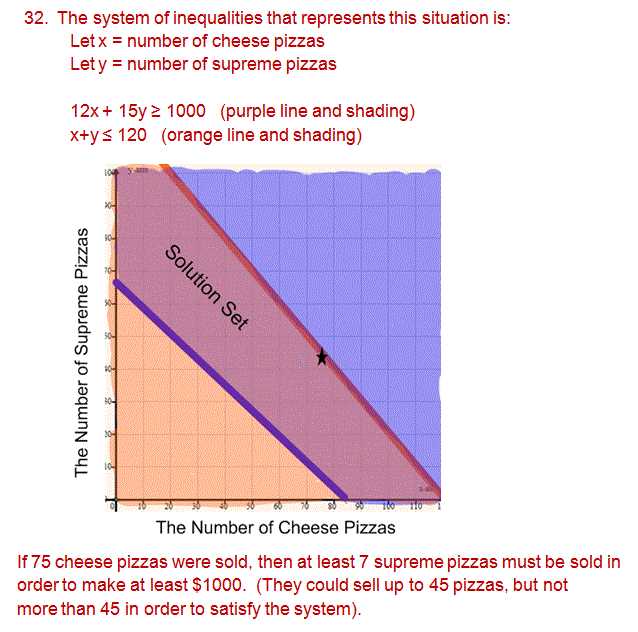
How to Tackle Inequalities on the Exam
Solving inequalities involves finding the range of values that satisfy a given mathematical condition. These problems often require different strategies compared to solving equations. Understanding the correct steps to take is essential for solving them accurately and efficiently, especially when dealing with multiple variables or complex expressions.
When faced with inequalities on a test, it is important to follow a clear method to ensure you don’t make mistakes. With the right approach, these problems can be handled just as easily as equations.
Steps for Solving Inequalities
- Step 1: Simplify the inequality by combining like terms and moving constant terms to one side of the inequality.
- Step 2: If necessary, divide or multiply both sides by a number. Be sure to reverse the inequality sign when multiplying or dividing by a negative number.
- Step 3: Check your solution by selecting a value from the solution range and testing it in the original inequality.
Key Points to Remember
- Multiplying/Dividing by Negative Values: Always remember to reverse the inequality sign when performing these operations.
- Graphing Solutions: Inequalities often involve expressing the solution on a number line, where you represent the values that satisfy the condition.
- Compound Inequalities: These are two inequalities combined into one. To solve them, treat them like two separate inequalities and then combine the results.
Example Inequality
| Problem | Solution |
|---|---|
| 3x – 4 | 1. Add 4 to both sides: 3x 2. Divide by 3: x |
By following these strategies and understanding key principles, you can effectively tackle inequality problems and avoid common mistakes.