Drawing Free Body Diagrams in Physics Classroom

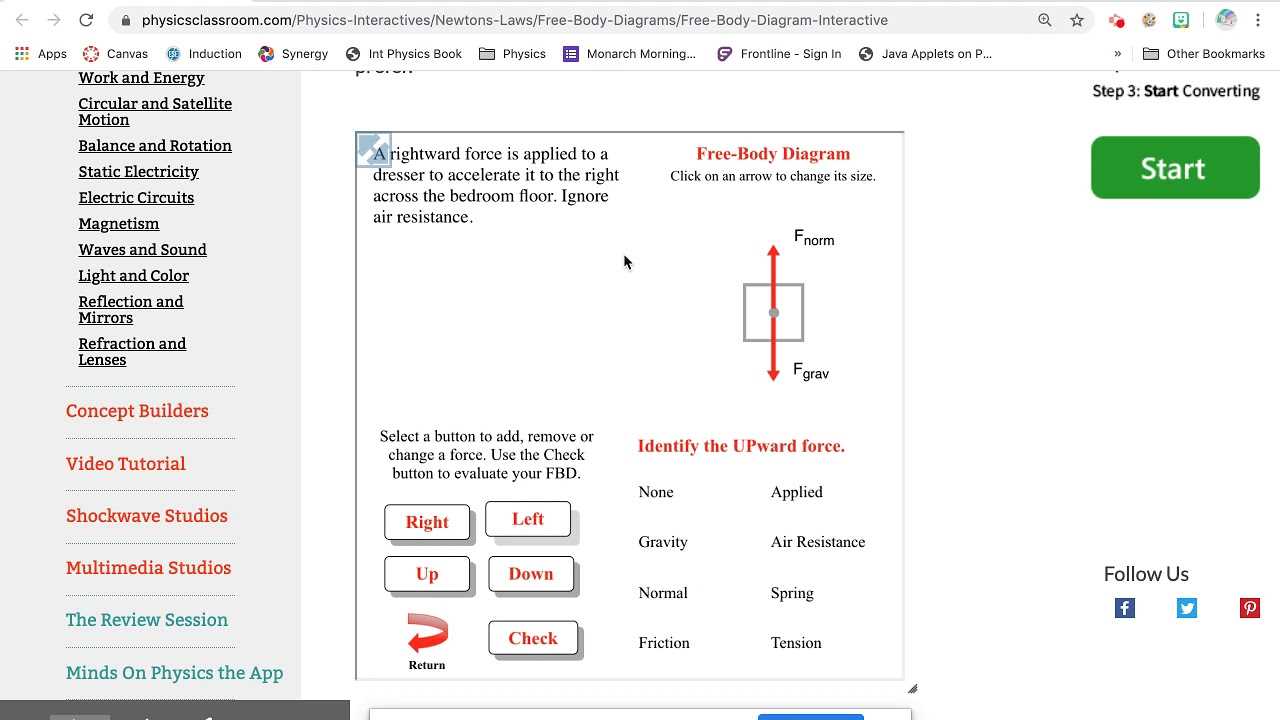
In any study of motion, representing the various forces acting on an object is crucial for analyzing and solving problems accurately. By visualizing these influences, we can simplify complex scenarios and break them down into manageable components. This method is essential for both theoretical understanding and practical applications in the physical world.

Identifying and analyzing the interactions between forces is a key skill that allows students to approach problems with clarity. Whether it’s determining the acceleration of an object or solving for unknown forces, the ability to depict these influences effectively is fundamental to mastering the subject. Such representations help bridge the gap between abstract concepts and real-world phenomena.

In this guide, we will explore the techniques and strategies for creating these helpful representations, focusing on how to structure and label each force. Understanding how to use these tools will not only improve problem-solving abilities but also deepen the overall comprehension of motion and forces in a variety of contexts.

Drawing Free Body Diagrams in Physics Classroom

Representing the forces acting on an object is essential for understanding its motion and behavior. This technique helps simplify complex scenarios, making it easier to analyze and solve problems. By visualizing these forces, students can better grasp how different variables interact, leading to clearer solutions in various motion-related problems.

Key Components of Force Representation

When creating a force representation, it’s important to focus on the relevant forces and their directions. Each force must be drawn to scale and labeled correctly to ensure accurate analysis. Below is a table that highlights common forces and their respective symbols for easy reference:

Force	Symbol	Description
Gravitational Force	Fg	The force exerted by the Earth pulling objects toward its center.
Normal Force	Fn	The force exerted by a surface to support the weight of an object resting on it.
Frictional Force	Ff	The resistive force that opposes the motion of an object sliding or rolling on a surface.
Applied Force	Fa	The force exerted by an object or person directly on an object.

Steps to Create an Effective Force Representation

To create an effective representation, follow these steps:

• Identify the object of interest and the forces acting on it.
• Choose an appropriate coordinate system, often aligning the horizontal and vertical axes with the forces’ directions.
• Draw arrows to represent the forces, ensuring that their lengths are proportional to their magnitudes.
• Label each force with its appropriate symbol, direction, and magnitude if available.

By following these guidelines, students can create clear and accurate representations that help solve complex problems related to motion. Understanding how to depict forces correctly is crucial for mastering the subject and applying it in real-world scenarios.

Understanding the Basics of Free Body Diagrams

To analyze the motion of an object and the forces acting upon it, it’s crucial to represent these interactions in a simplified manner. This method allows students to break down complex problems into understandable steps, facilitating clearer solutions. The key to successful problem-solving lies in accurately depicting and interpreting these forces, which can range from gravity to friction, depending on the situation.

In this section, we will focus on the fundamental concepts behind force representations and why they are essential for understanding object behavior. Here are the core principles:

• Force Identification: Recognizing the different forces acting on an object is the first step in creating an effective representation.
• Force Direction: Forces have both magnitude and direction. Understanding this is crucial when plotting the forces.
• Equilibrium vs. Motion: The representation helps determine whether an object is in equilibrium or experiencing acceleration.

Key Elements to Include

To ensure the accuracy of the representation, the following elements should always be considered:

1. Object Selection: Identify the object whose forces are being analyzed. This will help narrow down the relevant forces to include.
2. Force Symbols: Every force should be represented with a clear and consistent symbol, such as Fg for gravitational force or Fn for normal force.
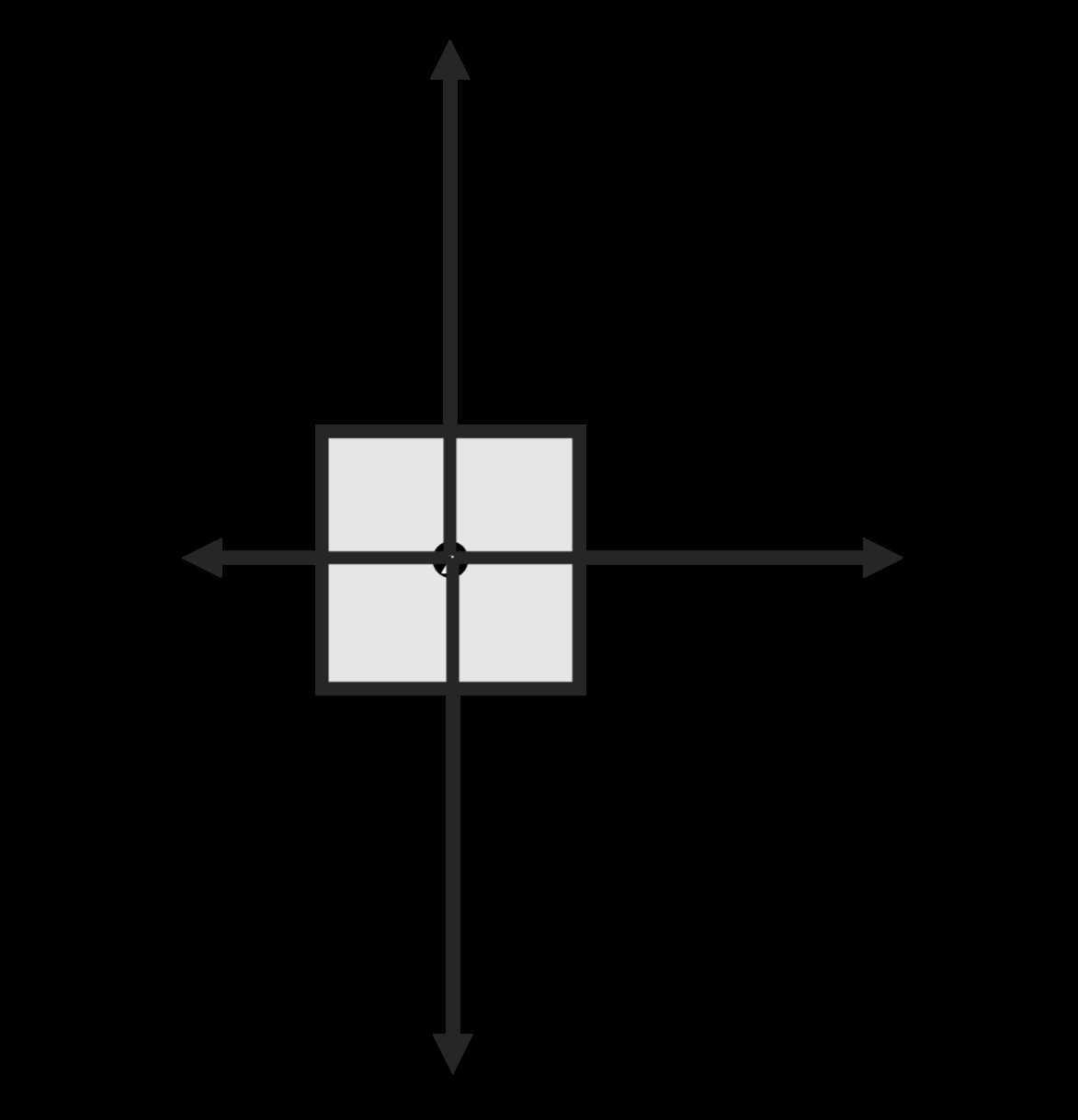
3. Coordinate System: Establish a coordinate system that aligns with the forces’ directions, typically with the x-axis for horizontal forces and the y-axis for vertical ones.
4. Force Magnitude: If available, the magnitude of each force should be indicated to ensure the correct scale is applied in problem-solving.

By understanding these basic concepts and elements, students can more effectively approach problems involving forces and motions, applying this knowledge in both theoretical and practical contexts. This foundational knowledge is key to mastering more complex scenarios in future studies.

Step-by-Step Guide to Drawing Diagrams

Creating an accurate representation of the forces acting on an object requires a systematic approach. By following a step-by-step process, students can ensure that they capture all relevant forces and depict them correctly. This methodical approach not only improves the clarity of the analysis but also leads to more accurate problem-solving.

Here is a simple guide to help you create a clear and effective force representation:

1. Identify the Object: Begin by selecting the object you want to analyze. This could be any object experiencing forces, such as a block on a surface or a moving car.
2. Isolate the Object: Visualize the object in isolation. Imagine that it is separated from its surroundings, and focus only on the forces acting on it.
3. Choose a Coordinate System: Select a coordinate system that will help you represent the directions of the forces. Typically, the horizontal axis (x-axis) is used for horizontal forces, and the vertical axis (y-axis) is used for vertical forces.
4. Label the Forces: Identify all forces acting on the object. These could include gravitational force, normal force, applied force, and frictional force. Label each one clearly and ensure they are drawn in the correct direction.
5. Draw Arrows for Forces: For each force, draw an arrow starting from the center of the object. The length of the arrow should be proportional to the magnitude of the force, and the direction should indicate where the force is applied.
6. Check for Accuracy: Review your representation to ensure that all relevant forces are included, labeled, and properly directed. Make sure that the diagram accurately reflects the situation being analyzed.

By following these steps, you can create a comprehensive and precise representation that will aid in analyzing the forces involved in any given scenario. This process is key for solving problems in mechanics and understanding how objects interact with their environment.

Common Mistakes to Avoid in FBDs

When creating representations of forces acting on an object, it is easy to overlook certain details or make errors that can lead to incorrect conclusions. These mistakes can stem from mislabeling forces, incorrect directions, or missing forces altogether. Being aware of these common pitfalls is essential for ensuring the accuracy of the analysis and preventing misunderstandings of the underlying physical principles.

Incorrect Force Directions

One of the most frequent mistakes is misrepresenting the direction of forces. Forces must be drawn as vectors with arrows indicating the direction in which they act. For example, gravitational force should always point downward, while the normal force should point upward from the surface. Failing to represent the correct directions can lead to confusion and incorrect calculations, especially when determining net force or acceleration.

Forgetting to Include Forces

Another common mistake is neglecting to include all relevant forces. In many cases, students may forget to represent forces such as friction, tension, or air resistance, depending on the problem. Each force acting on the object should be considered, even if it seems minor. Omitting one can drastically change the outcome of the analysis and lead to inaccurate results.

By avoiding these mistakes, you can ensure that your force representations are both complete and accurate, providing a solid foundation for solving problems and understanding the behavior of objects in motion.

How to Label Forces Correctly

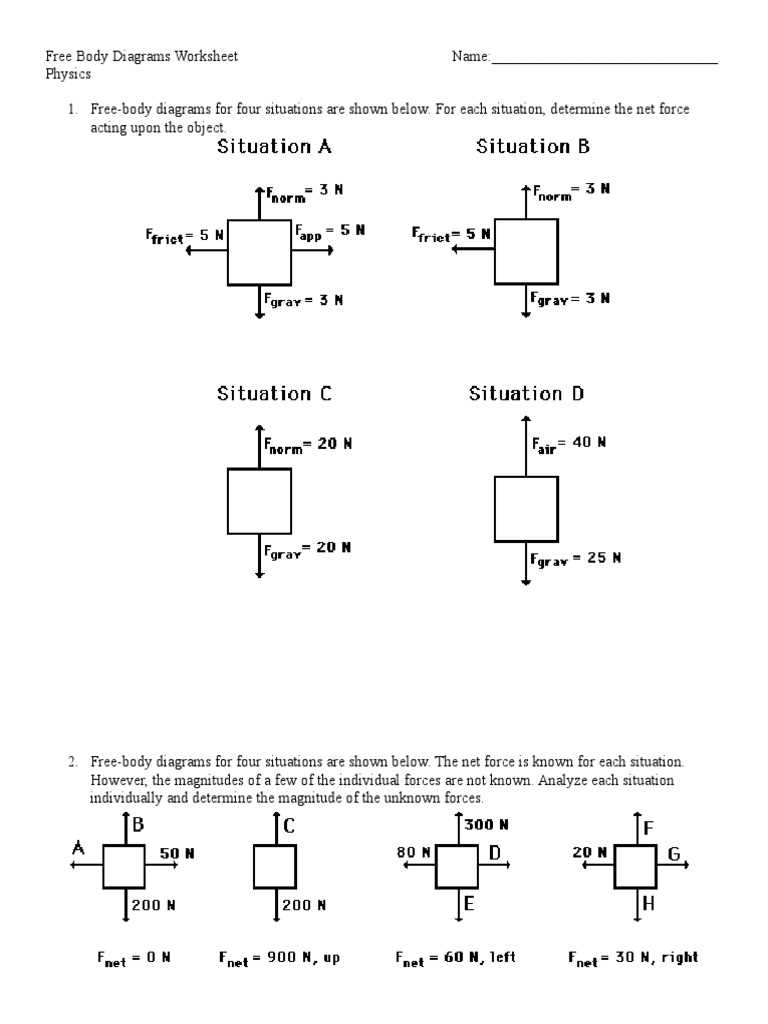
Labeling the forces acting on an object is a crucial step in creating a clear and accurate representation. Each force must be identified and labeled with its correct symbol, magnitude, and direction. Proper labeling ensures that the forces can be easily understood and analyzed, leading to more accurate results when solving problems.

First, ensure that each force is represented by a distinct arrow pointing in the correct direction. The length of the arrow should reflect the magnitude of the force. Next, label each force with the appropriate symbol, such as Fg for gravitational force, Fn for normal force, or Ff for friction. This allows anyone reading the representation to immediately understand which force is being referred to.

Additionally, if the problem involves numerical values for the forces, include the magnitude of each force next to its label. For example, instead of simply labeling a force as Fg, you might label it as Fg = 10 N if the gravitational force is known to be 10 Newtons. This provides a complete and accurate picture of the forces acting on the object.

Analyzing Newton’s Laws with FBDs

Newton’s laws of motion form the foundation of classical mechanics and are essential for understanding how objects move under the influence of forces. By using force representations, we can visually analyze how these forces affect an object’s acceleration and behavior. This approach provides a clear way to apply Newton’s three laws and solve problems related to motion.

Understanding Newton’s First Law

Newton’s first law, often called the law of inertia, states that an object at rest will stay at rest, and an object in motion will stay in motion unless acted upon by a net external force. This means that if the forces acting on an object are balanced, the object will either remain stationary or continue moving at a constant velocity. In the context of force representations, this can be seen when the vector sum of all forces equals zero.

• Balanced Forces: If the object is in equilibrium (no acceleration), the forces must cancel out. The representation will show arrows of equal magnitude but opposite direction, indicating no net force.
• Constant Velocity: When the forces are balanced, the object will either remain at rest or continue moving with a constant velocity, as per the first law.

Applying Newton’s Second Law

Newton’s second law explains how the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This relationship is captured by the equation F = ma, where F is the net force, m is the object’s mass, and a is its acceleration. When analyzing this law, the force representation helps us identify the net force, which is the vector sum of all individual forces acting on the object.

• Net Force Calculation: If the forces are unbalanced, the vector sum indicates the direction and magnitude of the net force, which determines the object’s acceleration.
• Acceleration Direction: The direction of acceleration is the same as the direction of the net force. The force representation shows how these forces combine to produce movement.

By using these visual tools, we can better understand the relationship between forces and motion, making it easier to solve problems involving Newton’s laws. This method is invaluable for analyzing both simple and complex scenarios, from static objects to those in motion.

Choosing the Right Coordinate System

Selecting an appropriate coordinate system is essential for effectively analyzing the forces acting on an object. The coordinate system helps in simplifying the problem, ensuring that each force is represented in terms of its components along the chosen axes. A well-chosen system makes it easier to break down forces into manageable components, ultimately simplifying the process of solving the problem.

When choosing a coordinate system, consider the following factors:

Factor	Description
Alignment with Forces	Choose axes that align with the direction of the forces, such as vertical and horizontal for gravity and normal forces.
Symmetry	If the problem involves symmetrical forces, aligning the axes along the symmetry lines can simplify the analysis.
Convenience	Select a system that reduces complex calculations, such as choosing a coordinate system that eliminates unnecessary components.
Object Motion	If the object is moving along a certain path, choose a system where the axes align with the direction of motion to make the problem easier to solve.

By aligning the axes with the most significant forces or the object’s motion, the representation of forces becomes more intuitive and easier to manipulate. The chosen coordinate system should make the problem-solving process straightforward, helping you to break down forces into their components with minimal confusion.

Types of Forces in Free Body Diagrams

When representing the forces acting on an object, it is essential to identify and include all the significant interactions between the object and its surroundings. Each force plays a vital role in determining the object’s motion, and understanding their types helps in analyzing the overall situation. Different forces can either cause the object to accelerate, remain in equilibrium, or change its direction of motion. Below are some of the most common forces encountered in these representations.

Gravitational Force

The gravitational force, often referred to as weight, is the force exerted by the Earth (or another celestial body) on an object. It acts downward, towards the center of the Earth. This force is proportional to the object’s mass and is a key factor in determining how objects behave when falling or resting on surfaces.

Normal Force

The normal force is the support force exerted by a surface to counteract the weight of an object resting on it. It acts perpendicular to the surface, balancing out the gravitational pull to prevent the object from falling through. This force is essential in scenarios where an object is on solid ground or any other supportive surface.

Frictional Force

Friction opposes the motion of an object sliding or attempting to slide across a surface. There are two primary types: static friction, which resists the initiation of motion, and kinetic friction, which resists motion once the object is already moving. The frictional force depends on the nature of the surfaces in contact and their relative motion.

Tension Force

Tension occurs in cables, ropes, or strings when they are pulled. This force is directed along the length of the object and is responsible for transmitting forces in systems such as elevators, pulleys, or ropes tied to objects. It acts in the direction of the pull, opposing forces that would otherwise move the object in the opposite direction.

Applied Force

This is the force exerted on an object by a person or another object. It can be a push or a pull and can be applied in any direction. Applied force plays a critical role in initiating or changing an object’s motion, depending on the magnitude and direction of the force.

Understanding the various types of forces and how they interact helps in accurately analyzing physical situations and solving related problems. Each force must be represented appropriately to ensure that the total force acting on an object is correctly calculated and interpreted.

Applying FBDs to Real-World Problems

In the real world, forces act on objects in a variety of ways, from the motion of vehicles to the behavior of structures. Understanding how to analyze these forces is crucial for solving practical problems in engineering, design, and even everyday scenarios. By using visual force representations, it becomes easier to break down complex systems into manageable parts and calculate the resulting effects of different forces. Whether it’s calculating the tension in a rope or understanding the forces at play in a building structure, these tools provide essential insights into how objects move or remain in equilibrium.

For example, consider a car moving along a road. Several forces are at play, such as the friction between the tires and the road, the force of gravity pulling the car downward, and the normal force from the road pushing upward. By applying force representations, engineers can calculate the car’s acceleration, design better safety features, or improve fuel efficiency by understanding the forces involved. Similarly, in construction, force analysis is used to ensure the stability of buildings and bridges by considering the various forces acting on the structure, including wind, weight, and tension in cables or beams.

In everyday life, simple applications such as moving furniture or lifting an object involve these same principles. For example, when lifting a heavy box, the upward force you apply must overcome the weight of the box, which is the gravitational force acting downward. By understanding these forces, individuals can make better decisions on how to move objects safely or efficiently. In all these cases, using force representations offers a systematic approach to understanding and solving problems involving motion and stability in the real world.

Using Free Body Diagrams in Dynamics

In the study of motion and forces, analyzing how objects move under the influence of various forces is essential. Representing the forces acting on an object allows us to apply Newton’s laws and predict the object’s behavior. This is especially useful in dynamics, where objects are in motion, and understanding the forces at play helps us calculate acceleration, velocity, and other critical parameters. By isolating an object and focusing on the forces that influence its motion, these visual tools provide a clear framework for solving problems in dynamic systems.

In dynamics, the most important step is breaking down complex motion into simpler parts. This involves:

• Identifying all forces: Start by listing all the forces acting on the object, including gravity, friction, applied forces, and others.
• Resolving forces into components: Break down forces into their components along specific axes to simplify calculations, especially when dealing with non-vertical or non-horizontal forces.
• Applying Newton’s Second Law: Use the relationship between forces and acceleration (F = ma) to calculate the object’s motion. This is crucial for understanding how the object accelerates in response to the applied forces.
• Analyzing the system’s behavior: Once forces are represented, the next step is to understand how they will influence the system over time, such as in the case of an object sliding down a ramp or a car accelerating on a road.

These steps are essential when applying this approach to dynamic problems, such as calculating the speed of a moving car, the trajectory of a projectile, or the forces acting on a suspended object. Without a clear understanding of how forces influence motion, predicting outcomes in real-world systems would be far more challenging. The visualization provided by these force representations enables engineers, scientists, and students to tackle complex dynamic scenarios with confidence and precision.

Free Body Diagrams for Rotational Motion

In rotational motion, objects experience forces that cause them to rotate around a central point or axis. Understanding these forces is essential for analyzing the behavior of spinning or rotating objects, such as wheels, gears, or even planets. While linear motion focuses on forces that act along straight lines, rotational motion involves additional factors, such as torque and angular acceleration, which are critical for understanding how objects rotate. By visualizing these forces, we can gain insights into how different components influence the rotation and predict the object’s behavior over time.

When analyzing rotational motion, the force representations must account for both the magnitude and direction of the applied forces, as well as their points of application. This often involves:

• Torque calculations: Forces that cause rotational motion apply torque, which is the rotational equivalent of force. Torque is calculated by multiplying the force by the distance from the axis of rotation.
• Moment of inertia: The resistance of an object to changes in its rotational motion depends on its moment of inertia, which is determined by the mass distribution relative to the axis of rotation.
• Angular acceleration: Just like linear acceleration, angular acceleration describes how quickly an object’s rotation speed changes. This is influenced by the applied torques and the moment of inertia.
• Balancing forces: Just as in linear motion, forces in rotational motion must be balanced to achieve equilibrium. If the sum of torques is zero, the object will not rotate.

By applying these principles, one can analyze systems involving rotational motion, such as gears in machinery, rotating wheels in vehicles, or even celestial bodies in orbit. The ability to accurately model the forces acting on rotating objects helps engineers design more efficient systems and allows scientists to predict the behavior of rotating objects in various fields, from mechanical engineering to astronomy.

Interpreting Diagrams for Equilibrium Situations

In many mechanical systems, objects can be in a state of balance, where all forces and moments acting on them cancel out, resulting in no movement or rotation. This condition is known as equilibrium. Understanding how to interpret force representations in equilibrium situations is essential for solving problems involving stationary or non-accelerating objects. The goal is to ensure that the forces are balanced in both magnitude and direction, leading to a stable configuration. Analyzing such scenarios requires careful attention to the interactions between the forces and their points of application.

In equilibrium situations, the key principles to remember are:

• Force balance: The sum of all forces acting on an object must be zero. This means that the forces in each direction (horizontal, vertical) must cancel each other out.
• Moment balance: The sum of all torques (moments) around any point must also be zero. This ensures that there is no rotation of the object around that point.
• Equal and opposite forces: For every action, there is an equal and opposite reaction. This principle must be evident in the representation of the forces acting on an object in equilibrium.

Steps to Analyze Equilibrium Situations

When interpreting force representations for equilibrium problems, follow these steps to ensure proper analysis:

1. Identify all forces: Make sure to account for all forces acting on the object, such as gravitational, normal, frictional, and applied forces.
2. Resolve forces into components: Break down complex forces into horizontal and vertical components to simplify the analysis.
3. Check for balance: Ensure that the sum of forces in both the horizontal and vertical directions is zero, indicating no net force acting on the object.
4. Check for rotational balance: Sum all torques about any point (often the object’s center of mass or a pivot point). The sum of all torques should also be zero, ensuring no rotation.

By following these steps, you can confidently interpret force representations in equilibrium situations and solve for unknown forces or moments. This method is widely used in structural engineering, machinery design, and various real-world applications where stability is crucial.

FBDs and Friction in Physics Problems

Friction is a critical force in many mechanical systems, often playing a key role in both static and dynamic scenarios. In problems involving moving objects or those at rest, understanding how friction interacts with other forces is essential for solving the system. To properly model these situations, it’s important to include friction in the force analysis. By accurately representing frictional forces in the system, one can determine how they affect the object’s motion or equilibrium. The magnitude and direction of frictional forces can significantly alter the behavior of the system, making it crucial to include them when constructing force representations.

Types of Friction in Force Representations

There are two primary types of friction to consider in force representations:

• Static Friction: This type of friction occurs when an object is not moving but is subject to an applied force. The frictional force adjusts to prevent motion up to a certain limit, beyond which sliding occurs.
• Kinetic Friction: This occurs once an object is in motion. Kinetic friction has a constant magnitude that resists the motion of the object and is generally smaller than static friction.

How to Include Friction in Force Models

When incorporating friction into force models, follow these steps to ensure accuracy:

1. Determine the normal force: The normal force is essential in calculating friction. It is the force exerted by a surface perpendicular to the object in contact with it. The greater the normal force, the larger the frictional force.
2. Calculate the frictional force: Use the appropriate friction coefficient for the material in contact. The static or kinetic frictional force is the product of the friction coefficient and the normal force.
3. Consider the direction of friction: Friction always opposes the motion of the object. If the object is moving, friction will act in the direction opposite to its motion. If the object is stationary, friction will act to prevent motion in response to any applied force.

By carefully including friction in your force analysis, you can more accurately model real-world systems. Whether dealing with objects at rest or in motion, friction plays a crucial role in determining the outcome of many problems, particularly in engineering and mechanical applications.

How to Draw Diagrams for Multiple Objects

When analyzing systems with more than one object, it is important to represent each object’s forces individually while accounting for interactions between them. By breaking down the problem into smaller parts, you can better understand the forces acting on each object and how they influence each other. In a system with multiple objects, each object needs its own representation, and you must consider both internal forces (such as tension or contact forces) and external forces (like gravity or applied forces). This process allows you to solve for unknown variables in complex systems effectively.

Below are steps for constructing accurate force representations for multiple objects:

1. Identify each object: Start by identifying the objects in the system and isolating them for individual analysis. Label each object clearly to avoid confusion.
2. Consider forces on each object: For every object, consider the forces acting on it from both external sources and other objects within the system.
3. Draw separate representations: For each object, draw a force model that includes all the forces acting on it. Make sure each object’s forces are depicted clearly to reflect the interactions between them.
4. Account for interactions: If objects are in contact, consider the forces that result from these interactions, such as tension, friction, or normal force. These forces need to be represented accurately between objects.
5. Analyze the system: Once each object’s forces are represented, analyze the entire system by considering how the forces interact. This may involve using Newton’s laws or other principles to find unknown quantities.

Example of Multiple Objects in a System

Consider a system with two objects connected by a rope, one hanging vertically and the other on a surface. The forces acting on each object would include:

Object	Forces Acting On It
Object 1 (hanging)	Weight (gravity), tension from the rope
Object 2 (on surface)	Weight (gravity), normal force from the surface, tension from the rope

By analyzing each object’s forces and their interactions, you can determine the acceleration of the system or the tension in the rope, allowing for a complete solution to the problem.

Free Body Diagrams in Projectile Motion

When analyzing motion in the air, it is important to understand the forces acting on an object at different points during its trajectory. For objects launched at an angle or falling under the influence of gravity, the forces can change depending on the object’s position and velocity. By representing these forces visually, we can better understand how they affect the object’s path and predict its motion at any given point. This approach helps break down the complex interaction between the forces and the object’s motion in a clear, structured way.

In projectile motion, the key forces involved are often gravity and air resistance, depending on the level of approximation. At the peak of the trajectory, the velocity becomes momentarily zero, but gravity is still acting on the object. As the object moves downward, gravity continues to accelerate it. Air resistance, if considered, acts opposite to the object’s motion, slowing it down over time.

Forces Acting on a Projectile

The forces involved in projectile motion typically include:

• Gravity: This force is constant and acts downward throughout the motion of the object, pulling it towards the Earth.
• Air resistance: Depending on the object’s speed and the medium through which it travels, air resistance may oppose the motion and reduce the object’s speed. In simplified problems, air resistance is often ignored.

Example of Projectile Motion

Imagine a ball thrown horizontally from a height. At the point of release, the forces acting on the ball are:

• Gravity, pulling it down
• No horizontal force (assuming no air resistance)

As the ball continues in motion, its horizontal velocity remains constant (neglecting air resistance), while its vertical velocity increases due to gravity, causing the object to follow a curved path.

By representing the forces at different points in time, we can solve for the object’s velocity, displacement, and other key quantities involved in its motion. This is an essential tool for analyzing projectiles in real-world scenarios, from sports to engineering applications.

​

Why Free Body Diagrams Are Essential in Physics

Understanding the forces acting on an object is key to solving many complex challenges in mechanics. Representing these interactions visually provides clarity and allows for precise calculations. By isolating the object and illustrating all external forces, one can better comprehend how each force influences motion and equilibrium.

Visualizing Forces is often the first step in analyzing problems related to motion or static situations. A proper representation of forces ensures that no detail is overlooked, leading to more accurate predictions and solutions. By isolating a single object in a system, the effects of forces like gravity, friction, and tension can be evaluated independently.

Breaking Down Complex Problems

In real-world scenarios, it can be challenging to identify how multiple forces interact. A clear and organized illustration of these forces provides an intuitive understanding of the dynamics at play. It simplifies otherwise complicated systems by focusing on one object at a time.

Improved Problem-Solving Techniques

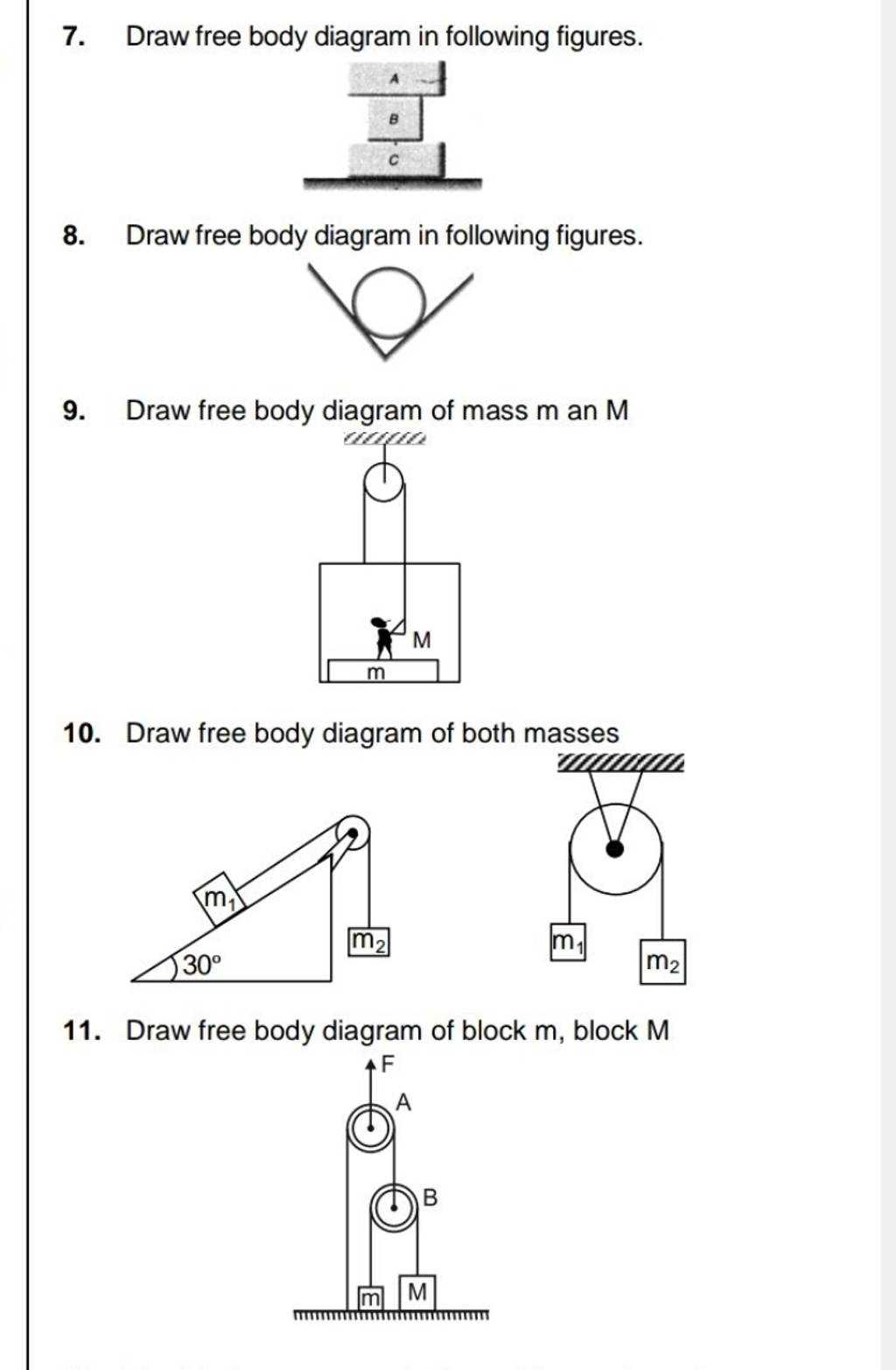
Having a visual model to refer to makes it easier to apply relevant equations and principles. This approach helps identify key variables and set up equations more efficiently, improving the overall problem-solving process.

Understanding FBDs in Complex Physics Scenarios

When tackling intricate problems involving multiple forces and interactions, isolating an object and analyzing its individual forces becomes essential. This method of visualization allows for a clear understanding of how various factors influence motion or stability. In complex situations, breaking down the forces step by step provides insights that are not immediately obvious from the problem description.

In scenarios with multiple objects or forces, careful attention to detail is required. A single diagram may not suffice to represent the entire system, and several separate illustrations may be necessary to capture all relevant interactions. By systematically considering each object and its corresponding forces, solutions can be built progressively.

Key Principles for Analyzing Complex Situations

• Identify all objects involved: Before anything else, clearly define the objects being considered. This step helps ensure that every force acting on them is accounted for.
• Separate interactions: For multi-object systems, separate the objects and create individual representations for each one to focus on the forces acting on it.
• Consider every force: Gravity, normal force, friction, tension, and applied forces are common but must always be verified in every situation.

Organizing Forces in Multiple-Object Systems

• Use symmetry: Many systems have symmetrical properties, which can simplify the analysis. Identifying such patterns allows for quicker and more efficient problem-solving.
• Apply Newton’s laws systematically: Once the forces are listed, applying the fundamental equations of motion for each object allows for the determination of unknowns like acceleration or force magnitudes.
• Consider external factors: In more advanced cases, factors such as air resistance or rotational motion may need to be incorporated into the analysis.